5.6: Poliedros regulares y semi-regulares

Última actualización
Guardar como PDF

Page ID: 108056

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Hemos visto cómo los polígonos regulares a veces encajan de borde a borde en el plano para crear inclinaciones de todo el plano. Al colocar en mosadas el plano, los ángulos de los polígonos que se encuentran borde a borde alrededor de cada vértice deben sumar 360°, o dos ángulos rectos. Si los ángulos en un vértice se suman a menos de 360°, entonces nos quedamos con un hueco vacío y dos bordes libres; y cuando estos dos bordes libres se unen, o se pegan entre sí, la figura del vértice se eleva fuera del plano y se convierte en una esquina tridimensional, o ángulo sólido.

Para formar tal esquina necesitamos al menos tres polígonos, o caras, y por lo tanto al menos tres aristas y tres caras se encuentran alrededor de cada vértice. Por ejemplo, tres cuadrados encajan muy bien juntos en el plano, pero dejan un hueco de 90°. Cuando los dos bordes de repuesto están pegados entre sí, el resultado es formar una esquina de un cubo, donde tenemos una figura de vértice que consta de tres 4 gones regulares: así nos referimos a esta figura de vértice como 4 ³.

Dada una esquina tridimensional, puede ser posible extender la construcción, repitiendo la misma figura de vértice en cada vértice. La forma resultante puede entonces “cerrarse” para formar un poliedro convexo. El supuesto de que en cada figura de vértice, los ángulos que se encuentran en ese vértice se suman a menos de 360°, significa que todas las esquinas luego se proyectan hacia afuera -que es aproximadamente lo que queremos decir cuando decimos que el poliedro es “convexo”.

Un polígono regular es una disposición de finitamente muchos segmentos de línea congruentes, con dos segmentos de línea que se encuentran en cada vértice (y nunca cruzan, o se encuentran internamente), y con todos los vértices iguales; un polígono regular se puede inscribir en un círculo (Problema 36), y así encierra un subconjunto convexo del plano. En el mismo espíritu, un poliedro regular es una disposición de finitamente muchos polígonos regulares congruentes, con dos polígonos que se encuentran en cada borde, y con el mismo número de polígonos en un solo ciclo alrededor de cada vértice, encerrando un subconjunto convexo de espacio tridimensional (es decir, el poliedro separa los puntos restantes de 3D en los que se encuentran 'dentro' y los que se encuentran 'afuera', y el segmento de línea que une dos puntos cualesquiera de la superficie poliédrica no contiene puntos que se encuentran fuera del poliedro).

Las restricciones importantes aquí son las suposiciones: que los polígonos se encuentran borde a borde con exactamente dos polígonos que se encuentran en cada borde; que el mismo número de polígonos se encuentran alrededor de cada vértice; y que el número total de polígonos, o caras, es finito. La suposición de que la figura es convexa debe verse como una restricción adicional temporal, lo que significa que los ángulos en los polígonos que se encuentran en cada vértice tienen una suma inferior a 360°.

Problema 186 Una figura de vértice se va a formar ajustando juntos p-gones regulares, de borde a borde, para una p. fija. Si hay q de estos p-gones en un vértice, denotamos la figura del vértice por p ^q. Si los ángulos en cada vértice se suman a menos de 360°, demostrar que las únicas cifras de vértice posibles son ^{3 3}, 3 ⁴, 3 ⁵, 4 ³, 5 ³.

El vértice figura 4 ³ se realiza por la forma en que los ejes positivos se encuentran en el vértice (0,0,0), donde

la unidad cuadrada (0, 0,0), (1, 0,0), (1,1,0), (0,1,0) en el plano XY (con la ecuación z = 0) cumple
la unidad cuadrada (0,0,0), (1,0,0), (1,0,1), (0,0,1) en el plano xz (con la ecuación y = 0), y
la unidad cuadrada (0, 0, 0), (0,1,0), (0,1,1), (0, 0,1) en el plano yz (con ecuación x = 0).

Si incluimos un octavo vértice (1, 1, 1), y

la unidad cuadrada (0, 0, 1), (1, 0, 1), (1, 1, 1), (0, 1, 1) en el plano con la ecuación z = 1,
la unidad cuadrada (0,1,0), (1,1,0), (1,1,1), (0,1,1) en el plano con la ecuación y = 1,
la unidad cuadrada (1,0,0), (1,1,0), (1,1,1), (1,0,1) en el plano con la ecuación x = 1,

vemos que los ocho vértices tienen el mismo vértice figura 4 ³. De ahí que la posible figura de vértice 4 ³ en el Problema 186 surge como la figura de vértice de un poliedro regular, es decir, el cubo.

Si seleccionamos los cuatro vértices cuyas coordenadas tienen suma impar A = (1, 0, 0), B = (0,1, 0), C = (0, 0,1), D = (1,1,1), entonces la distancia entre cualquiera de estos vértices es igual a $\sqrt{2}$ , por lo que cada triple de vértices (como (1, 0, 0), (0,1,0), (0, 0,1)) define un ABC regular de 3 gones, con tres de esos 3 gones que se encuentran en cada vértice de ABCD. De ahí que la posible figura de vértice ^{3 3} en el Problema 186 surge como la figura de vértice de un poliedro regular, es decir, el tetraedro regular (tetra = cuatro; edra = caras).

Problema 187 Con A = (1,0,0) etc. como arriba, anote las coordenadas de los seis puntos medios de los bordes del tetraedro regular ABCD (o equivalentemente, los seis centros de las caras del cubo original). Cada borde del tetraedro regular se encuentra con otros cuatro bordes del tetraedro regular (por ejemplo, AB se encuentra con AC y AD en un extremo, y BC y BD en el otro extremo). Elija una arista AB y su punto medio P. Calcular la distancia de P a los puntos medios Q, R, S, T de los cuatro bordes con los que se encuentra AB (es decir, los puntos medios de AB, AD, BD, BC respectivamente). Confirmar que los triángulos ΔPQR, ΔPRS, ΔPST, ΔPTQ son todos regulares de 3 gones, y que la figura del vértice en P es de tipo 3 ⁴. Concluir que la posible figura de vértice 3 ⁴ en el Problema 186 surge como la figura de vértice de un poliedro regular PQRSTU, es decir, el octaedro regular (octa = ocho; hedra = caras).

Problema 188

(a) Un tetraedro regular ABCD tiene bordes de longitud 2, y se asienta con su base BCD sobre la mesa. Encuentra la altura de A por encima de la base.

b) Un octaedro regular ABCDEF tiene cuatro triángulos que se encuentran en cada vértice.

(i) Que los cuatro triángulos que se encuentran en A sean ABC, ACD, ADE, AEB. Demostrar que BCDE debe ser un cuadrado.

(ii) Supongamos que todos los triángulos tienen bordes de longitud 2, y que el octaedro se asienta con una cara BCF sobre la mesa, junto al tetraedro regular de la parte (a). ¿Cuál de estos dos sólidos es el más alto?

Problema 189 Que O = (0, 0, 0), A = (1,0,0), B = (0,1,0), C = (0,0,1) sean cuatro vértices del cubo como se describe después del Problema 186 anterior. Dibuje segmentos de línea iguales y paralelos (inicialmente de longitud desconocida 1 — 2 a) a través de los centros de cada par de caras opuestas, corriendo en las tres direcciones paralelas a OA, o a OB, o a OC

de $N = (a, \frac{1}{2}, 0)$ a $P = (1 - a, \frac{1}{2}, 0)$ y de $Q = (a, \frac{1}{2}, 1)$ a $R = (1 - a, \frac{1}{2}, 1)$
de $S = (\frac{1}{2}, 0, a)$ a $T = (\frac{1}{2}, 0, 1 - a)$ y de $U = (\frac{1}{2}, 1, a)$ a $V = (\frac{1}{2}, 1, 1 - a)$
de $W = (0, a, \frac{1}{2})$ a $X = (0, 1 - a, \frac{1}{2})$ y de $Y = (1, a, \frac{1}{2})$ a $Z = (1, 1 - a, \frac{1}{2})$ .

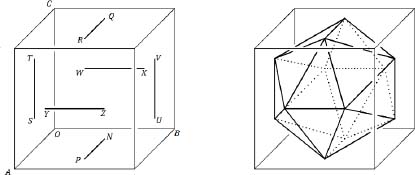
$Ch05-002.jpeg$

Figura 4: Construcción del icosaedro regular.

Estos son para formar los 12 vértices y seis de los 30 bordes (de longitud 1 — 2a) de un poliedro, ver Figura 4. Los otros 24 bordes unen cada uno de estos 12 vértices a sus cuatro vecinos naturales en caras adyacentes del cubo, para formar las 20 caras triangulares del poliedro: por ejemplo,

N une: a S; a W; a X; y a U.

(i) Demostrar que NS = NW = NX = NU y calcular la longitud de NS.

(ii) Elegir el valor del parámetro a para garantizar que NP = NS, de manera que las cinco caras triangulares que se encuentran en el vértice N sean todas triángulos equiláteros, y cada figura de vértice del poliedro resultante tenga entonces la figura de vértice 3 ⁵.

El poliedro se llama icosaedro regular (icosa = veinte, hedra = caras).

En el párrafo anterior al Problema 187 construimos el dual del cubo marcando el circuncentro de cada una de las seis caras cuadradas del cubo, y luego uniendo cada circuncentro a sus cuatro vecinos naturales. Ahora construimos el dual del icosaedro regular exactamente de la misma manera. Cada uno de los 20 circuncentros de las 20 caras triangulares de un icosaedro regular tiene tres vecinos naturales (es decir, los circuncentros de las tres caras triangulares vecinas). Si construimos los 30 bordes que unen estos 20 circuncentros, los cinco circuncentros de los cinco triángulos en cada figura de vértice del icosaedro regular forman un pentágono regular, que se convierte en una cara del poliedro dual, por lo que obtenemos 12 pentágonos regulares (uno por cada vértice del icosaedro regular), con tres pentágonos que se encuentran en cada vértice del poliedro dual para dar una figura de vértice 5 ³ en cada uno de los 20 vértices, los cuales forman un dodecaedro regular.

De ahí que cada una de las cinco posibles figuras de vértice del Problema 186 pueda ser realizada por un poliedro regular. A estos se les llama a veces los sólidos platónicos porque Platón (c. 428-347 a.C.) a menudo los usaba como ejemplos ilustrativos en sus escritos sobre filosofía.

Construir los cinco poliedros regulares es parte de la esencia de las matemáticas para todos. En contraste, lo que viene después (en el Problema 190) puede verse como “opcional” en esta etapa. Las ideas son dignas de mención, pero es mejor posponer los detalles para un día lluvioso.

Así como clasificó los tilings semi-regulares en la Sección 5.4, así se puede buscar poliedros semi-regulares. Un poliedro es semi-regular si todas sus caras son polígonos regulares (posiblemente con diferentes números de aristas), encajando de borde a borde, con exactamente el mismo anillo de polígonos alrededor de cada vértice, la figura del vértice del poliedro. El problema 190 utiliza “el método de análisis” -combinando aritmética simple, desigualdades y un poco de perspicacia geométrica- para lograr una notable clasificación completa de poliedros semi-regulares. Por lo general se dice que hay trece poliedros semirregulares individuales (excluyendo los cinco poliedros regulares); pero uno de ellos tiene una figura de vértice que se extiende a un poliedro de dos maneras diferentes, siendo cada una el reflejo de la otra. Además hay dos familias infinitas, a saber,

los prismas n-gonales, que constan de dos n-gones regulares paralelos, con el superior colocado exactamente por encima del inferior, estando los dos unidos por un cinturón de n cuadrados (así con la figura de vértice n. 4 ²); y
los antiprismas n-gonales, que consisten en dos n-gones regulares paralelos, pero con el n-gon superior girado en un ángulo de n radianes con relación al inferior, estando los dos unidos por un cinturón de 2n triángulos equiláteros (así con una figura de vértice n. 3 ³).

Observe que el cubo también puede interpretarse como un “prisma 4-gonal”, y el octaedro regular puede interpretarse como un “antiprisma 3-gonal”. Los interesados en los poliedros regulares y semi-regulares son referidos al libro clásico Modelos matemáticos de H.M. Cundy y A.P. Rollett.

Problema 190 Encuentra posibles combinaciones de tres o más polígonos regulares cuyos ángulos se suman a menos de 360°, y de ahí derivar una lista completa de posibles figuras de vértices para un poliedro semi-regular (convexo). Intenta eliminar esas supuestas figuras de vértice que no pueden extenderse a un poliedro semi-regular.