5.8: Arcos circulares y sectores circulares

La longitud se define para los segmentos de línea recta, y el área se define en términos de rectángulos; ninguna medida se define para formas con límites curvos, a menos que, es decir, se puedan diseccionar astutamente y las piezas se reordenen para formar una línea recta, o un rectángulo.

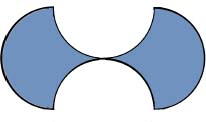
Figura 5: Mancuerna.

Problema 201 Cuatro semicírculos idénticos de radio 1 encajan entre sí para hacer la forma de mancuerna que se muestra en la Figura 5. Encuentra el área exacta encerrada sin usar la fórmula para el área de un círculo.

En general, dar sentido a la longitud y el área para formas con límites curvos requiere que combinemos un poco de imaginación con lo que sabemos sobre segmentos de líneas rectas y polígonos. Nuestro objetivo aquí es conducir a los resultados familiares para la longitud de los arcos circulares y el área de sectores circulares. Pero primero necesitamos explorar el perímetro y área de polígonos regulares, y la superficie de prismas y pirámides.

Como tantas veces en las matemáticas, para dar sentido al perímetro y área de polígonos regulares necesitamos mirar más allá de sus valores reales (que variarán según el tamaño del polígono), y en su lugar interpretar estos valores como una función de algún parámetro normalizador, como el radio. Los cálculos serán más sencillos si primero pruebas un resultado general.

Problema 202

(a) Un n-gon regular y un 2n-gon regular se inscriben en un círculo de radio 1. El n-gon regular tiene bordes de longitud s _n = s, mientras que el regular 2 n-gon tiene bordes de longitud s _2n = t. Demostrar que

$$t^2=2-\sqrt{4-s^2}.$$

(b) Un “2-gon” regular inscrito en el círculo unitario es apenas un diámetro (repetido dos veces), por lo que tiene dos bordes idénticos de longitud s ₂ = 2. Utilice el resultado de la parte (a) para calcular la longitud de borde s ₄ de un 4 gon regular, y la longitud de borde s ₈ de un 8 gon regular inscrito en el mismo círculo.

(c) Un 6 gón regular inscrito en el círculo unitario tiene una longitud de borde s ₆ igual al radio 1. Usa el resultado de la parte (a) para calcular la longitud de borde s ₃ de un 3 gónregular inscrito en el círculo unitario, y la longitud de borde s ₁₂ de un 12 gon regular inscrito en el círculo unitario.

(d) En el Problema 185 vimos que un 5 gon regular inscrito en el círculo unitario tiene longitud de borde

$$s_5=\frac{\sqrt{10-2\sqrt{5}}}{2}.$$

Usa el resultado de la parte (a) para calcular la longitud de borde s ₁₀ de un 10 gon regular inscrito en el mismo círculo.

Problema 203

(a) Un n-gon regular se inscribe en un círculo de radio r.

(i) Encontrar el perímetro exacto p _n (en forma surd): cuando n = 3; cuando n = 4; cuando n = 5; cuando n = 6; cuando n = 8; cuando n = 10; cuando n = 12.

ii) Comprobar que, por cada n:

$$p_n=c_n\times r$$

para alguna constante c _n, donde

$$c_3<c_4<c_5<c_6<c_8<c_{10}<c_{12}\cdots$$

(b) Un n-gon regular se circunscribe alrededor de un círculo de radio r.

(i) Encontrar el perímetro exacto P _n (en forma surd): cuando n = 3; cuando n = 4; cuando n = 5; cuando n = 6; cuando n = 8; cuando n = 10; cuando n = 12.

ii) Comprobar que, por cada n:

$$p_n=c_n\times r$$

para alguna constante C _n, donde

$$c_3<c_4<c_5<c_6<c_8<c_{10}<c_{12}\cdots$$

c) Explicar por qué c ₁₂ < C ₁₂.

Del Problema 203 se deduce que

De ahí

• los perímetros p _n y P _n de n -gones regulares inscritos en, o circunscritos alrededor de, un círculo de radio r tienen todos la misma forma:

  $$(inscribed)p_n=c_n\times r;(circumscribed)P_n=C_n\times r.$$

• Los perímetros de los n-gones regulares inscritos aumentan con n, pero permanecen menores que el perímetro del círculo, mientras que
• todos los perímetros de los n-gones regulares circunscritos disminuyen con n, pero permanecen mayores que el perímetro del círculo.
• el perímetro P del círculo parece tener la forma P = K × r, donde la relación

  $$K=\frac{\text{perímetro}}{\text{radio}}$$

  satisface

  $$c_3<c_4<c_5<c_6<c_8<c_{10}<\cdots <K<\cdots <C_{10}<C_8<C_6<C_5<C_4<C_3.$$

  En particular, el valor de la constante K se encuentra en algún lugar entre c ₄₂ = 6.21.. y C12 = 6.43. Si ahora definimos el cociente K para que sea igual a “2π”, vemos que

  $$(perimeterofcircleofradiusr)=$$2πr,

  donde π denota alguna constante que se encuentra entre 3.1 y 3.22

  En este espíritu uno podría reinterpretar las dos primeras viñetas como definiendo dos secuencias de constantes “π _n" y “π _n" para$n⩾3$, de tal manera que

• (perímetro de un n-gon regular con circunradio r) = 2π _n r, donde

  $${\pi }_3=\frac{3\sqrt{3}}{2}=2.59\cdots ,{\pi }_4=2\sqrt{2}=2.82\cdots ,{\pi }_5=\frac{5\sqrt{10-2\sqrt{5}}}{4}=2.93\cdots ,{\pi }_6=3,$$

  etc.,

  y

• (perímetro de un n-gon regular con inradio r) = 2π _n r, donde

  $${\Pi }_3=3\sqrt{3}=5.19\cdots ,{\Pi }_4=4,{\Pi }_5=5\sqrt{5-2\sqrt{5}}=3.63\cdots ,{\Pi }_6=2\sqrt{3}=3.46\cdots ,$$

  etc.,

  Por otra parte

  $${\pi }_3<{\pi }_4<{\pi }_5<{\pi }_6<{\pi }_8<\cdots <\pi <\cdots <{\Pi }_8<{\Pi }_6<{\Pi }_5<{\Pi }_4<{\Pi }_3.$$

Problema 204 Encuentra la longitud exacta (en términos de π)

i) de un semicírculo de radio r;

ii) de un cuarto de círculo de radio r;

(iii) de la longitud de un arco de un círculo de radio r que subtiende un ángulo θ radianes en el centro.

En el siguiente problema seguimos una secuencia similar de pasos para concluir que el cociente

$$L=\frac{\text{área de círculo de radio}r}{r^2}$$

también es constante. La sorpresa radica en el hecho de que esta constante diferente está tan estrechamente relacionada con la constante K anterior.

Problema 205

(a) Un n-gon regular se inscribe en un círculo de radio r.

(i) Encontrar el área exacta a _n (en forma surd): cuando n = 3; cuando n = 4; cuando n = 5; cuando n = 6; cuando n = 8; cuando n = 10; cuando n = 12.

ii) Comprobar que, por cada n:

$$a_n=d_n\times r^2$$

para alguna constante d _n, donde

$$d_3<d_4<d_5<d_6<d_8<d_{10}<d_{12}\cdots$$

(b) Un n-gon regular se circunscribe alrededor de un círculo de radio r.

(i) Encontrar el área exacta A _n (en forma surd): cuando n = 3; cuando n = 4; cuando n = 5; cuando n = 6; cuando n = 8; cuando n = 10; cuando n = 12.

ii) Comprobar que, por cada n:

$$A_n=D_n\times r^2$$

para alguna constante D _n, donde

$$D_3>D_4>D_5>D_6>D_8>D_{10}>D_{12}\cdots$$

c) Explicar por qué d ₁₂ < D ₁₂.

Del Problema 205 se deduce que

• las áreas a _n y A _n de n-gones regulares inscritos en, o circunscritos alrededor de, un círculo de radio r tienen todas la misma forma:

$$(inscribed)a_n=d_n\times r^2;(circumscribed)A_n=D_n\times r^2.$$

• Todas las áreas de n-gones regulares inscritos aumentan con n, pero permanecen menores que el área del círculo, mientras que
• todas las áreas de los n-gones regulares circunscritos disminuyen con n, pero permanecen mayores que el área del círculo, de donde
• el área A del círculo parece tener la forma A = L × r ², donde la relación

  $$L=\frac{\text{área de círculo de radio}r}{\text{radio al cuadrado}}$$

  satisface

  $$d_3<d_4<d_5<d_6<d_8<d_{10}\cdots <L<\cdots <D_{10}<D_8<D_6<D_4<D_3.$$

  En particular, el valor de L se encuentra en algún lugar entre d ₁₂ = 3 y$D_{12}=12(2-\sqrt{3})=3.21\cdots$. La sorpresa radica en el hecho de que la constante L es exactamente la mitad de la constante K, es decir, L = π, entonces

  $$(areaofcircleofradiusr)=\pi r^2.$$

El siguiente problema ofrece una explicación heurística para esta sorpresa.

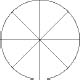
Figura 6: Círculo cortado en 8 rebanadas.

Problema 206 Un ABCDE 2n-gon regular. se inscribe en un círculo de radio r. los 2n radios OA, OB,... unir el centro O a los 2n vértices cortar el círculo en 2n sectores, cada uno con ángulo$\frac{\pi }{n}$(Figura 6).

Estos 2n sectores se pueden reorganizar para formar un “casi rectángulo”, orientándolos alternativamente para apuntar “arriba” y “abajo”. ¿En qué sentido tiene este “casi rectángulo” “height = r” y πr?

Problema 207

(a) Encontrar una fórmula para el área superficial de un cilindro derecho con altura h y con base circular de radio r.

(b) Encontrar una fórmula similar para el área superficial de un prisma derecho con altura h, cuya base es un n-gon regular con inradio r.

Problema 208

(a) Encontrar el área exacta (en términos de π)

i) de un semicírculo de radio r;

ii) de un cuarto de círculo de radio r;

(iii) de un sector de un círculo de radio r que subtiende un ángulo θ radianes en el centro.

(b) Encontrar el área de un sector de un círculo de radio 1, cuyo perímetro total (incluyendo los dos radios) es exactamente la mitad del círculo mismo.

Problema 209

(a) Encontrar una fórmula para el área superficial de un cono circular derecho con base de radio r y altura inclinada l.

(b) Encontrar una fórmula similar para el área superficial de una pirámide derecha con ápice A cuya base BCDE.. es un n-gon regular con inradio r.

Problema 210

a) Encontrar una expresión que implique”$\mathrm{pecado}\frac{\pi }{n}$” para la relación

$$\frac{\text{perímetro de regular inscrito}n\text{-gon}}{\text{perímetro de círculo circunscrito}}.$$

b) Encontrar una expresión que implique”$\mathrm{bronceado}\frac{\pi }{n}$” para la relación

$$\frac{\text{perímetro de regular circunscrito}n\text{-gon}}{\text{perímetro de círculo inscrito}}.$$

Problema 211

a) Encontrar una expresión que implique”$\mathrm{pecado}\frac{2\pi }{n}$” para la relación

$$\frac{\text{área de regular inscrito}n-\text{gon}}{\text{área de círculo circunscrito}}.$$

b) Encontrar una expresión que implique”$\mathrm{bronceado}\frac{\pi }{n}$” para la relación

$$\frac{areaofcircumscribedregularn-\text{gon}}{areaofinscribedcircle}.$$