5.11: Loci y secciones cónicas

Última actualización
Guardar como PDF

Page ID: 108051

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Esta sección ofrece una breve introducción a ciertos loci clásicamente importantes en el plano. La palabra locus aquí se refiere al conjunto de todos los puntos que satisfacen alguna condición geométrica simple; y todos los ejemplos de esta sección se basan en la noción de distancia desde un punto y desde una línea.

Dado un punto O y un r real positivo, el locus de puntos a distancia r de O es precisamente el círculo de radio r con centro O. Si r < 0, entonces el locus está vacío; mientras que si r = 0, el locus consiste en el punto O solo.

Dada una línea m y una r real positiva, el lugar geométrico de todos los puntos a distancia r de la línea m consiste en un par de líneas paralelas, una a cada lado de la línea m. Dado un círculo de radio r, y un número real positivo d < r; el locus de puntos a la distancia d del círculo consiste en dos círculos, cada uno concéntrico con el círculo dado (uno dentro del círculo dado y otro exterior). Si d > r, el locus consiste en un solo círculo fuera del círculo dado.

Dados dos puntos A y B, el lugar geométrico de los puntos que son equidistantes de A y de B es precisamente la bisectriz perpendicular del segmento lineal AB. Y dadas dos líneas m, n el locus de puntos que son equidistantes de m y de n toma formas diferentes según m y n son, o no, paralelos.

Si m y n son paralelos, entonces el locus consiste en una sola línea paralela a m y n y a medio camino entre ellos.
Si m y n se encuentran en X (digamos), entonces el locus consiste en el par de líneas perpendiculares a través de X, que bisecan los cuatro ángulos en X.

Problema 220 Dado un punto F y una línea m, elija m como eje x y la línea a través de F perpendicular a m como eje y. Deje que F tenga coordenadas (0, 2a).

(i) Encontrar la ecuación que define el locus de puntos que son equidistantes de F y de m.

(ii) ¿La ecuación sugiere una elección más natural de los ejes y, por lo tanto, una ecuación más simple para el locus?

El locus, o curva, en Problema 220 se llama parábola; el punto F se llama foco de la parábola, y la línea m se llama directriz. En general, la relación

“la distancia de X a F”: “la distancia de X a m”

se llama la excentricidad de la curva. De ahí que la parábola tenga excentricidad e = 1.

La parábola tiene muchas propiedades maravillosas: por ejemplo, es el camino seguido por un proyectil bajo la fuerza de la gravedad; si se ve como la superficie de un espejo, una parábola refleja los rayos del sol (o cualquier haz paralelo) a un solo punto: el foco F. Dado que la única variable en la construcción de la parábola es la distancia “2a” entre el foco y la directriz, podemos escalar distancias para ver que dos parábolas de aspecto diferente deben de hecho ser similares entre sí, al igual que con dos círculos cualesquiera. (Es difícil no inferir de las gráficas que y = 10 x ² es una parábola “delgada”, y que $y = (\frac{1}{10}) x^{2}$ es una parábola “gorda”. Pero el primero se puede reescribir en la forma 10 y =( 10 x) ², y el segundo se puede reescribir en la forma $(\frac{y}{10}) = {(\frac{x}{10})}^{2}$ , por lo que cada uno es una versión re-escalada de Y = X ².)

Hasta el momento hemos considerado que los loci definidos por algún par de distancias son iguales, o en la relación 1:1. Cosas más interesantes empiezan a suceder cuando consideramos condiciones en las que dos distancias están en una relación fija distinta a 1:1.

Problema 221

a) Dados dos puntos A, B, con AB = 6. Encuentra el locus de todos los puntos X tal que AX: BX = 2:1.

b) Dados los puntos A, B, con AB = 2 b y un número real positivo f. Encuentra el locus de todos los puntos X tal que AX: BX = f: 1.

Problema 222

a) Dados los puntos A, B, con AB = 2 c y un número real a > c. Encuentra el locus de todos los puntos X tal que AX + BX = 2 a.

(b) Dado un punto F y una línea m, encontrar el lugar geométrico de todos los puntos X de tal manera que la relación

distancia de X al punto F: distancia de X a la línea m

es una constante positiva e < 1.

c) Demostrar que las partes (a) y (b) dan diferentes formas de especificar la misma curva, o locus.

Problema 223

a) Dados los puntos A, B, con AB = 2 c, y un número real positivo a. Encuentra el locus de todos los puntos X tal que | AX - BX | = 2 a.

(b) Dado un punto F y una línea m, encontrar el lugar geométrico de todos los puntos X de tal manera que la relación

distancia de X al punto F: distancia de X a la línea m

es una constante e > 1.

c) Demostrar que las partes (a) y (b) dan diferentes formas de especificar la misma curva, o locus.

El problema 221 a veces se presenta en forma de broma leve.

Dos dragones están durmiendo, uno en A y otro en B. El Dragón A puede correr el doble de rápido que el dragón B. Un espécimen de homo sapiens se coloca en el segmento de línea AB, dos veces más lejos de A que de B, y astutamente decide arrastrarse silenciosamente lejos, manteniendo la relación de sus distancias de A y de B (de manera que hacen que sea igualmente difícil para cualquiera de los dragones atraparlo si despiertan).

El locus que emerge generalmente viene como una sorpresa: si el hombre se apega a su restricción impuesta, moviéndose para que su posición X satisfaga XA = 2. ¡XB, luego sigue un círculo y aterriza de regreso donde empezó! Al círculo se le llama círculo de Apolonio, y a veces se hace referencia a los puntos A y B como sus focos.

El locus en el Problema 222 es una elipse - con focos A (o F = (-ae, 0)) y B (= (ae, 0)), y con directriz m (la línea $y = - \frac{a}{e}$ ; la línea y = a es la segunda directrix de la elipse). La descripción de “foco-foco” en la parte (a) es simétrica bajo reflexión tanto en la línea AB como en la bisectriz perpendicular de AB. La descripción de “foco-directrix” en (b) es claramente simétrica en la línea a través de F perpendicular a m; pero es una sorpresa encontrar que la ecuación

$\frac{x^{2}}{a^{2}} + \frac{y^{2}}{a^{2} (1 - e^{2})} = 1$

también es simétrico bajo reflexión en el eje y. Si establecemos b ² = a ² (1 - e ²), la ecuación toma la forma

$\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1,$

que cruza el eje x cuando x = ± a, y cruza el eje y cuando y = + b. En su forma estándar, solemos elegir las coordenadas de modo que b < a: el segmento de línea de (- a, 0) a (a, 0) se denomina entonces el eje mayor, y la mitad de él (digamos de (0,0) a (a, 0)) - de longitud a - se llama semieje mayor; el segmento de línea de (0, - b) a (0, b) se llama el eje menor, y la mitad del mismo (digamos de (0, 0) a (0, b)) - de longitud b - se llama el semi-eje menor.

La forma de la ecuación muestra que una elipse se obtiene a partir de un círculo unitario estirando por un factor “a” en la dirección x, y por un factor “b” en la dirección y. Esto implica que el área de una elipse es igual a π ab (ya que cada pequeño s por s cuadrado que surge en la definición del “área” del círculo unitario se estira en un “rectángulo as by bs”). Sin embargo, la ecuación no nos dice nada sobre el perímetro de una elipse. Los intentos de precisar el perímetro de una elipse dieron lugar en el ^siglo XVIII al tema de las “integrales elípticas”.

Al igual que las parábolas, las elipses surgen naturalmente en muchos escenarios importantes. Por ejemplo, Kepler (1571-1630) descubrió que las órbitas planetarias no son circulares (como se había creído anteriormente), sino elipses, con el Sol en un foco (una conjetura que luego fue explicada por Isaac Newton (1642-1727)). Además, la tangente a una elipse en cualquier punto X está igualmente inclinada a las dos líneas XA y XB, de manera que un haz que emerge de un foco se refleja en cada punto de la elipse para que todos los rayos reflejados pasen por el otro foco.

La curva en el Problema 223 es una hipérbola - con focos A (o F = (-ae, 0)) y B (= (ae, 0)), y con directriz m (la línea $y = - \frac{a}{e}$ ; la línea $y = \frac{a}{e}$ es la segunda directrix de la hipérbola). La descripción de “foco-foco” en la parte (a) es simétrica bajo reflexión tanto en la línea AB como en la bisectriz perpendicular de AB. La descripción de “foco-directrix” en (b) es claramente simétrica en la línea a través de F perpendicular a m; pero es una sorpresa encontrar que la ecuación

$\frac{x^{2}}{a^{2}} - \frac{y^{2}}{a^{2} (e^{2} - 1)} = 1$

también es simétrico bajo reflexión en el eje y. Al igual que las parábolas y elipses, las hipérbolas surgen naturalmente en muchos escenarios importantes, en las matemáticas y en las ciencias naturales.

Todos estos loci fueron introducidos y estudiados por los antiguos griegos sin el beneficio de la geometría de coordenadas y ecuaciones. Se introdujeron como secciones transversales planas de un cono, es decir, como extensiones naturales de líneas rectas y círculos (ya que el cono doblemente infinito es la superficie trazada cuando se gira una línea alrededor de un eje a través de un punto en esa línea). La equivalencia de la definición foco-directriz en Problemas 220, 222 y 223 y secciones transversales de un cono se desprende del siguiente problema. Las cinco construcciones del Problema 224 funcionan con el cono doblemente infinito, que podemos representar como x ² + y ² = (rz) ² - aunque esta representación no es estrictamente necesaria para las derivaciones. La superficie del cono doble se extiende hasta el infinito en ambas direcciones, y se obtiene tomando la línea y = rz en el plano yz (donde r > 0 es constante), y girándola alrededor del eje z. Las imágenes de esta línea girada se llaman generadores del cono; y el punto por el que pasan todos (es decir, el origen) se llama vértice del cono.

Problema 224 (Esferas de Dandelin's: Dandelin (1794-1847))

(a) Describir las secciones transversales obtenidas cortando dicho cono doble por un plano horizontal (es decir, un plano perpendicular al eje z). ¿Y si el plano de corte es el plano xy?

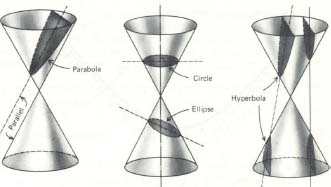
$Ch05-007.jpeg$

Figura 7: Secciones cónicas.

b) i) Describir la sección transversal obtenida cortando dicho cono por un plano vertical a través del origen, o ápice.

ii) ¿Qué sección transversal se obtiene si el plano de corte pasa por el ápice, pero no es vertical?

(c) Dar una descripción cualitativa de la curva obtenida como sección transversal del cono si cortamos el cono por un plano que es paralelo a un generador: e.g., el plano y - rz = c.

(i) ¿Qué pasa si c = 0?

(ii) Ahora supongamos que el plano de corte es paralelo a un generador, pero no pasa por el ápice del cono, por lo que podemos suponer que el plano corta solo la mitad inferior del cono. Inserte una pequeña esfera dentro de la mitad inferior del cono y por encima del plano de corte, e infle la esfera tanto como sea posible, hasta que toque el cono alrededor de un círculo horizontal (el “círculo de contacto con el cono”), y toque el plano en un solo punto F. Deje que el plano horizontal del “círculo de contacto con el cono” se encuentre con el plano de corte en la línea m. Demostrar que cada punto de la curva transversal es equidistante del punto F y de la línea m - y así es una parábola.

d) i) Dar una descripción cualitativa de la curva obtenida como sección transversal del cono si cortamos el cono por un plano que es menos empinado que un generador, pero que no pasa por el ápice, y así corta a través del cono.

(ii) Podemos suponer que el plano corta solo la mitad inferior del cono. Inserte una pequeña esfera dentro de la mitad inferior del cono y por encima del plano de corte (es decir, en el mismo lado del plano de corte que el ápice del cono), e infle la esfera tanto como sea posible, hasta que toque el cono alrededor de un círculo horizontal, y toque el plano en un solo punto F. Deje que el plano horizontal del círculo de contacto se encuentre con el plano de corte en la línea m. Demostrar que, para cada punto X en la curva transversal, la relación

“distancia de X a F”: “distancia de X a m” = e: 1

es constante, con e < 1, y también lo es una elipse.

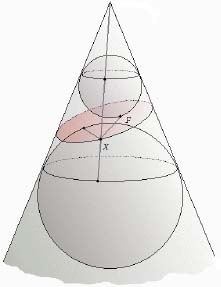
$Ch05-008.jpeg$

Figura 8: La sección cónica que surge en el Problema 224 (d).

(e) i) Dar una descripción cualitativa de la curva obtenida como sección transversal si cortamos el cono por un plano que es más empinado que un generador, pero no pasa por el ápice (y por lo tanto corta ambas mitades del cono)?

(ii) Podemos estar seguros de que el avión corta la mitad inferior del cono (así como la mitad superior). Inserte una pequeña esfera dentro de la mitad inferior del cono y en el mismo lado del plano de corte que el ápice, e infle la esfera tanto como sea posible, hasta que toque el cono alrededor de un círculo horizontal, y toque el plano en un solo punto F. Deje que el plano horizontal del círculo de contacto se encuentre con el plano de corte en la línea m. Demostrar que, para cada punto X en la curva transversal, la relación

“distancia de X a F”: “distancia de X a m” = e: 1

es constante, con e > 1, y también lo es una hipérbola.

El problema 224 revela una correspondencia notable. No es difícil demostrar algebraicamente que cualquier ecuación cuadrática en dos variables x, y representa un punto, o un par de líneas rectas cruzadas (posiblemente idénticas), o una parábola, o una elipse, o una hipérbola: es decir, cambiando las coordenadas, la ecuación cuadrática puede ser transformado a una de las formas normalizadas obtenidas en esta sección. De ahí que las posibles curvas cuadráticas sean precisamente las mismas que las posibles secciones transversales de un cono. Esta notable equivalencia se ve reforzada aún más por los numerosos contextos naturales en los que surgen estas secciones cónicas.