5.6: Problemas de aplicación con funciones exponenciales y logarítmicas
- Page ID
- 113674
En esta sección, usted:
- revisar estrategias para resolver ecuaciones derivadas de fórmulas exponenciales
- resolver problemas de aplicación que involucran funciones exponenciales y funciones logarítmicas
ESTRATEGIAS PARA RESOLVER ECUACIONES QUE CONTIENEN EXPONENTES
Al resolver problemas de aplicación que involucran funciones exponenciales y logarítmicas, debemos prestar mucha atención a la posición de la variable en la ecuación para determinar la forma correcta de resolver la ecuación que investigamos resolviendo ecuaciones que contienen exponentes.
Supongamos que tenemos una ecuación en la forma: value = coeficiente (base) exponente
Consideramos cuatro estrategias para resolver la ecuación:
ESTRATEGIA A: Si el coeficiente, la base y el exponente son todos conocidos, solo necesitamos evaluar la expresión de coeficiente (base) exponente para evaluar su valor.
ESTRATEGIA B: Si la variable es el coeficiente, evalúe la expresión para exponente (base). Entonces se convierte en una ecuación lineal que resolvemos dividiendo para aislar la variable.
ESTRATEGIA C: Si la variable está en el exponente, utilice logaritmos para resolver la ecuación.
ESTRATEGIA D: Si la variable no está en el exponente, sino que está en la base, use raíces para resolver la ecuación.
A continuación examinamos cada estrategia con uno o dos ejemplos de su uso.
ESTRATEGIA A: Si el coeficiente, la base y el exponente son todos conocidos, solo necesitamos evaluar la expresión de coeficiente (base) exponente para evaluar su valor.
Supongamos que el precio de una acción está subiendo a una tasa de 7% anual, y que sigue aumentando a esta tasa. Si el valor de una acción de esta acción es de 43 dólares ahora, encuentra el valor de una acción de esta acción dentro de tres años.
Solución
Let\(y\) = el valor de la acción después de\(t\) años:\(y = ab^t\)El problema nos dice que\(a\) = 43 y\(r\) = 0.07, entonces\(b = 1+ r = 1+ 0.07 = 1.07\)
Por lo tanto, la función es\(y = 43(1.07)^t\).
En este caso sabemos que\(t\) = 3 años, y necesitamos evaluar\(y\) cuando\(t\) = 3.
Al término de 3 años, el valor de esta acción será
\[y=43(1.07)^{3}=\$ 52.68 \nonumber \]
ESTRATEGIA B: Si la variable es el coeficiente, evalúe la expresión para exponente (base). Entonces se convierte en una ecuación lineal que resolvemos dividiendo para aislar la variable.
El valor de un auto nuevo se deprecia (disminuye) después de su compra. Supongamos que el valor del automóvil se deprecia según un modelo de decaimiento exponencial. Supongamos que el valor del automóvil es de 12000 dólares al término de 5 años y que su valor ha ido disminuyendo a razón de 9% anual. Encuentra el valor del auto cuando era nuevo.
Solución
Dejar\(y\) ser el valor del auto después de\(t\) años:\(y = ab^t\),\(r\) = -0.09 y\(b = 1+r = 1+(-0.09) = 0.91\)La función es\(y = a(0.91)^t\)
En este caso sabemos que cuando\(t\) = 5, entonces\(y\) = 12000; sustituyendo estos valores da
\[12000 = a(0.91)^5 \nonumber \]
Tenemos que resolver por el valor inicial a, el precio de compra del auto cuando es nuevo.
Primero evalúe (0.91) 5; luego resuelva la ecuación lineal resultante para encontrar\(a\).
\[ 1200 = a(0.624) \nonumber \]
\(a=\frac{12000}{0.624} = \$ 19,230.77\); El valor del auto era de 19.230.77 dólares cuando era nuevo.
ESTRATEGIA C: Si la variable está en el exponente, utilice logaritmos para resolver la ecuación.
Un parque nacional tiene una población de 5000 venados en el año 2016. Los conservacionistas están preocupados porque la población de venados está disminuyendo a razón de 7% anual. Si la población sigue disminuyendo a este ritmo, ¿cuánto tiempo tardará hasta que la población sea solo de 3000 venados?
Solución
\(y\)Sea el número de venados en el parque nacional\(t\) años después del año 2016:\(y = ab^t\)\(r\)= -0.07 y\(b = 1+r = 1+(-0.07) = 0.93\) y la población inicial es\(a\) = 5000
La función de decaimiento exponencial es\(y = 5000(0.93)^t\)
Para encontrar cuando la población será de 3000, sustituto\(y\) = 3000
\[ 3000 = 5000(0.93)^t \nonumber \]
A continuación, divide ambos lados por 5000 para aislar la expresión exponencial
\ [\ begin {array} {l}
\ frac {3000} {5000} =\ frac {5000} {5000} (0.93) ^ {2}\\
0.6=0.93^ {t}
\ end {array}\ nonumber\]
Reescriba la ecuación en forma logarítmica; luego use la fórmula de cambio de base para evaluar.
\[t=\log _{0.93}(0.6) \nonumber \]
\(t = \frac{\ln(0.6)}{\ln(0.93)}=7.039\)años; Después de 7.039 años, hay 3000 venados.
Nota: En Ejemplo\(\PageIndex{3}\), necesitábamos indicar la respuesta a varios decimales de precisión para que permaneciera precisa. Evaluar la función original usando un valor redondeado de\(t\) = 7 años da un valor cercano a 3000, pero no exactamente 3000.
\[y=5000(0.93)^{7}=3008.5 \text { deer } \nonumber \]
Sin embargo usando\(t\) = 7.039 años produce un valor de 3000 para la población de venados
\[ y=5000(0.93)^{7.039}=3000.0016 \approx 3000 \text { deer } \nonumber \]
Un video publicado en YouTube inicialmente tuvo 80 reproducciones tan pronto como se publicó. El número total de visualizaciones hasta la fecha ha ido aumentando exponencialmente de acuerdo con la función de crecimiento exponencial\(y = 80e^{0.2t}\), donde\(t\) representa el tiempo medido en días desde que se publicó el video. ¿Cuántos días lleva hasta que 2500 personas hayan visto este video?
Solución
Dejar\(y\) ser el número total de vistas\(t\) días después de que se publique inicialmente el video.
Se nos da que la función de crecimiento exponencial es\(y = 80e^{0.2t}\) y queremos encontrar el valor de\(t\) para el cual\(y\) = 2500. Sustituye\(y\) = 2500 en la ecuación y usa logaritmo natural para resolver\(t\).
\[2500 = 80e^{0.12t} \nonumber \]
Dividir ambos lados por el coeficiente, 80, para aislar la expresión exponencial.
\ [\ begin {array} {c}
\ frac {2500} {80} =\ frac {80} {80} e^ {0.12 t}\\
31.25=e^ {0.12 t}
\ end {array}\ nonumber\]
Reescribir la ecuación en forma logarítmica
\[ 0.12t = \ln(31.25) \nonumber \]
Divide ambos lados por 0.04 para aislar\(t\); luego usa tu calculadora y su función de registro natural para evaluar la expresión y resolver\(t\).
\ [\ begin {array} {l}
\ mathrm {t} =\ frac {\ ln (31.25)} {0.12}\
\ mathrm {t} =\ frac {3.442} {0.12}\
\ mathrm {t}\ aproximadamente 28.7\ text {días}
\ end {array}\ nonumber\]
Este video tendrá 2500 vistas totales aproximadamente 28.7 días después de haber sido publicado.
ESTRATEGIA D: Si la variable no está en el exponente, sino que está en la base, utilizamos raíces para resolver la ecuación.
Es importante recordar que solo usamos logaritmos cuando la variable está en el exponente.
Un estadístico crea un sitio web para analizar estadísticas deportivas. Su plan de negocios establece que su objetivo es acumular 50 mil seguidores a finales de 2 años (dentro de 24 meses). Espera que si logra este objetivo su sitio sea comprado por un medio de noticias deportivas. La base de usuarios inicial de personas inscritas como resultado de la publicidad previa al lanzamiento es de 400 personas. Encuentre la tasa de crecimiento mensual necesaria si la base de usuarios va a acumular hasta 50,000 usuarios al final de 24 meses.
Solución
Dejar\(y\) ser la base total de usuarios\(t\) meses después de que se lance el sitio.
La función de crecimiento para este sitio es\(y = 400(1+r)^t\);
No conocemos la tasa de crecimiento\(r\). Sí sabemos que cuando\(t\) = 24 meses, entonces\(y\) = 50000.
Sustituir los valores de\(y\) y\(t\); entonces tenemos que resolver para\(r\).
\[5000 = 400(1+r)^{24} \nonumber \]
Divide ambos lados por 400 para aislar (1+r) 24 en un lado de la ecuación
\ [\ begin {array} {l}
\ frac {50000} {400} =\ frac {400} {400} (1+r) ^ {24}\
125 =( 1+r) ^ {24}
\ end {array}\ nonumber\]
Debido a que la variable en esta ecuación está en la base, usamos raíces:
\ [\ begin {array} {l}
\ sqrt [24] {125} =1+r\\
125^ {1/24} =1+r\\
1.2228\ aprox 1+r\\
0.2228\ aprox r
\ end {array}\ nonumber\]
La base de usuarios del sitio web necesita aumentar a razón de 22.28% mensuales para acumular 50,000 usuarios al final de 24 meses.
Una hoja informativa sobre la dependencia de la cafeína del Centro Médico Johns Hopkins afirma que la vida media de la cafeína en el cuerpo es de entre 4 y 6 horas. Suponiendo que la vida media típica de la cafeína en el cuerpo es de 5 horas para la persona promedio y que una taza de café típica tiene 120 mg de cafeína.
- Escribe la función decaimiento.
- Encuentra la tarifa por hora a la que la cafeína sale del cuerpo.
- ¿Cuánto tiempo tarda hasta que solo 20 mg de caffieno aún estén en el cuerpo?
www.Hopkinsmedicine.org/psyc... fact_sheet.pdf
Solución
a. dejar\(y\) ser la cantidad total de cafeína en el cuerpo\(t\) horas después de tomar el café.
La función de decaimiento exponencial\(y = ab^t\) modela esta situación.
La cantidad inicial de cafeína es\(a\) = 120.
No sabemos\(b\) o\(r\), pero sabemos que la vida media de la cafeína en el cuerpo es de 5 horas. Esto nos dice que cuando\(t\) = 5, entonces queda la mitad de la cantidad inicial de cafeína que queda en el cuerpo.
\ [\ begin {array} {l}
y=120 b^ {t}\
\ frac {1} {2} (120) =120 b^ {5}\\
60=120 b^ {5}
\ end {array}\ nonumber\]
Divide ambos lados por 120 para aislar la expresión\(b^5\) que contiene la variable.
\ [\ begin {array} {l}
\ frac {60} {120} =\ frac {120} {120}\ mathrm {b} ^ {5}\\
0.5=\ mathrm {b} ^ {5}
\ end {array}\ nonumber\]
La variable está en la base y el exponente es un número. Usa raíces para resolver\(b\):
\ [\ begin {array} {l}
\ sqrt [5] {0.5} =\ mathrm {b}\\
0.5^ {1/5} =\ mathrm {b}\\
0.87=\ mathrm {b}
\ end {array}\ nonumber\]
Ahora podemos escribir la función de decaimiento para la cantidad de cafeína (en mg.) que queda en el cuerpo\(t\) horas después de tomar una taza de café con 120 mg de cafeína
\[y=f(t)=120(0.87)^{t} \nonumber \]
b. utilizar\(b = 1 + r\) para encontrar la tasa de decaimiento\(r\). Porque\(b = 0.87 < 1\) y la cantidad de cafeína en el cuerpo va disminuyendo con el tiempo, el valor de\(r\) será negativo.
\ [\ begin {array} {l}
0.87=1+r\\
r=-0.13
\ end {array}\ nonumber\]
La tasa de descomposición es de 13%; la cantidad de cafeína en el cuerpo disminuye 13% por hora.
c. Para encontrar el tiempo en el que sólo quedan 20 mg de cafeína en el cuerpo, sustituirlo\(y\) = 20 y resolver por el valor correspondiente de\(t\).
\ [\ begin {array} {l}
y=120 (.87) ^ {t}\\
20=120 (.87) ^ {t}
\ end {array}\ nonumber\]
Divide ambos lados por 120 para aislar la expresión exponencial.
\ [\ begin {array} {l}
\ frac {20} {120} =\ frac {120} {120}\ left (0.87^ {t}\ right)\\
0.1667=0.87^ {t}
\ end {array}\ nonumber\]
Reescribe la expresión en forma logarítmica y usa el cambio de fórmula base
\ [\ begin {array} {l}
t=\ log _ {0.87} (0.1667)\\
t=\ frac {\ ln (0.1667)} {\ ln (0.87)}\ approx 12.9\ text {horas}
\ end {array}\ nonumber\]
Después de las 12.9 horas, quedan 20 mg de cafeína en el cuerpo.
EXPRESANDO FUNCIONES EXPONENCIALES EN LAS FORMAS y = ab t e y = ae kt
Ahora que hemos desarrollado nuestras habilidades para resolver ecuaciones, revisamos la cuestión de expresar funciones exponenciales de manera equivalente en las formas\(y = ab^t\) y\(y = ae^{kt}\)
Ya hemos determinado que si se le da la forma\(y = ae^{kt}\), es sencillo de encontrar\(b\).
Para los siguientes ejemplos, supongamos que\(t\) se mide en años.
- \(y = 3500e^{0.25t}\)Exprese en forma\(y = ab^t\) y encuentre la tasa de crecimiento porcentual anual.
- \(y = 28000e^{-0.32t}\)Exprese en forma\(y = ab^t\) y encuentre la tasa de decaimiento porcentual anual.
Solución
a. Expresar\(y = 3500e^{0.25t}\) en la forma\(y = ab^t\)
\ [\ begin {array} {l}
y=a e^ {k t} =a b^ {t}\\
a\ izquierda (e^ {k}\ derecha) ^ {t} =a b^ {t}
\ end {array}\ nonumber\]
Así\(e^k=b\)
En este ejemplo\(b=e^{0.25} \approx 1.284\)
Reescribimos la función de crecimiento como y = 3500 (1.284 t)
Para encontrar\(r\), recuerde que\(b = 1+r\)
\ [\ begin {aligned}
&1.284=1+r\\
&0.284=\ mathrm {r}
\ end {alineado}\ nonumber\]
La tasa de crecimiento continuo es de\(k\) = 0.25 y la tasa de crecimiento porcentual anual es de 28.4% anual.
b. Expresar\(y = 28000e^{-0.32t}\) en la forma\(y = ab^t\)
\ [\ begin {array} {l}
y=a e^ {k t} =a b^ {t}\\
a\ izquierda (e^ {k}\ derecha) ^ {t} =a b^ {t}
\ end {array}\ nonumber\]
Así\(e^k=b\)
En este ejemplo\(\mathrm{b}=e^{-0.32} \approx 0.7261\)
Reescribimos la función de crecimiento como y = 28000 (0.7261 t)
Para encontrar\(r\), recuerde que\(b = 1+r\)
\ [\ begin {array} {l}
0.7261=1+r\\
0.2739=r
\ end {array}\ nonumber\]
La tasa de decaimiento continuo es\(k\) = -0.32 y la tasa anual de decaimiento porcentual es 27.39% anual.
En la oración, omitimos el signo negativo al afirmar la tasa de decaimiento porcentual anual porque hemos utilizado la palabra “decaimiento” para indicar que r es negativo.
- Expresar\(y = 4200 (1.078)^t\) en la forma\(y =ae^{kt}\)
- Expresar\(y = 150 (0.73)^t\) en la forma\(y =ae^{kt}\)
Solución
a. Expresar\(y = 4200 (1.078)^t\) en la forma\(y =ae^{kt}\)
\ [\ begin {array} {l}
\ mathrm {y} =\ mathrm {a} e^ {\ mathrm {k} t} =\ mathrm {ab} ^ {\ mathrm {t}}\
\ mathrm {a}\ left (e^ {\ mathrm {k}}\ right) ^ {\ mathrm {t}} =\ mathrm {ab} ^ {^\ mathrm rm {t}}\\
e^ {\ mathrm {k}} =\ mathrm {b}\\
e^ {k} =1.078
\ end {array}\ nonumber\]
Por lo tanto\(\mathrm{k}=\ln 1.078 \approx 0.0751\)
Reescribimos la función de crecimiento como\(y = 3500e^{0.0751t}\)
b. Expresar\(y =150 (0.73)^t\) en la forma\(y = ae^{kt}\)
\ [\ begin {array} {l}
y=a e^ {k t} =a b^ {t}\\
a\ izquierda (e^ {k}\ derecha) ^ {t} =a b^ {t}\\
e^ {k} =b\\
e^ {k} =0.73
\ end {array}\ nonumber\]
Por lo tanto\(\mathrm{k}=\ln 0.73 \approx-0.3147\)
Reescribimos la función de crecimiento como\(y = 150e^{-0.3147t}\)
UNA APLICACIÓN DE UNA FUNCIÓN LOGARÍTMICA
Supongamos que hoy invertimos 10,000 dólares y queremos saber cuánto tiempo tardará en acumularse hasta una cantidad especificada, como $15,000. El tiempo\(t\) necesario para alcanzar un valor futuro\(y\) es una función logarítmica del valor futuro:\(t = g(y)\)
Supongamos que Vinh invierte 10000 dólares en una inversión que gana 5% al año. Quiere saber cuánto tardaría su inversión en acumularse a 12000 dólares, y cuánto tiempo tardaría en acumularse a $15000.
Solución
Comenzamos por escribir la función de crecimiento exponencial que modela el valor de esta inversión en función del tiempo desde que se invierten inicialmente los $10000
\[y=10000(1.05)^{t} \nonumber \]
Dividimos ambos lados por 10000 para aislar la expresión exponencial en un lado.
\[\frac{y}{10000}=1.05^{t} \nonumber \]
A continuación reescribimos esto en forma logarítmica para expresar el tiempo en función del valor futuro acumulado. Usaremos notación de función y llamaremos a esta función\(g(y)\).
\[\mathrm{t}=\mathrm{g}(\mathrm{y})=\log _{1.05}\left(\frac{\mathrm{y}}{10000}\right) \nonumber \]
Utilice la fórmula de cambio de base para expresar\(t\) como una función del\(y\) uso del logaritmo natural:
\[\mathrm{t}=\mathrm{g}(\mathrm{y})=\frac{\ln \left(\frac{\mathrm{y}}{10000}\right)}{\ln (1.05)} \nonumber \]
Ahora podemos usar esta función para responder a las preguntas de Vinh.
Para encontrar el número de años hasta que el valor de esta inversión sea de $12,000, sustituimos\(y\) = $12,000 en función\(g\) y evaluamos\(t\):
\[\mathrm{t}=\mathrm{g}(12000)=\frac{\ln \left(\frac{12000}{10000}\right)}{\ln (1.05)}=\frac{\ln (1.2)}{\ln (1.05)}=3.74 \text { years } \nonumber \]
Para encontrar el número de años hasta que el valor de esta inversión sea de $15,000, sustituimos\(y\) = $15,000 en función\(g\) y evaluamos\(t\):
\[\mathrm{t}=\mathrm{g}(15000)=\frac{\ln \left(\frac{15000}{10000}\right)}{\ln (1.05)}=\frac{\ln (1.5)}{\ln (1.05)}=8.31 \text { years } \nonumber \]
Antes de terminar esta sección, investigamos la gráfica de la función\(\mathrm{t}=\mathrm{g}(\mathrm{y})=\frac{\ln \left(\frac{\mathrm{y}}{10000}\right)}{\ln (1.05)}\). Vemos que la función tiene la forma general de funciones logarítmicas que examinamos en la sección 5.5. A partir de los puntos trazados en la gráfica, vemos que la función\(g\) es una función creciente pero aumenta muy lentamente.
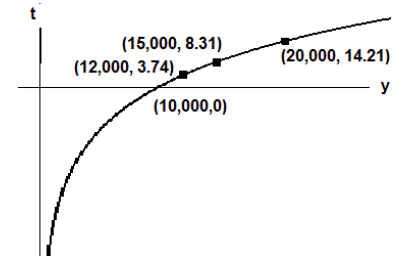
Si consideramos solo la función\(\mathrm{t}=\mathrm{g}(\mathrm{y})=\frac{\ln \left(\frac{\mathrm{y}}{10000}\right)}{\ln (1.05)}\), entonces el dominio de la función sería\(y > 0\), todos los números reales positivos, y el rango para\(t\) sería todos los números reales.
En el contexto de este problema de inversión, la inversión inicial en tiempo\(t\) = 0 es\(y\) =$10,000. Los valores negativos para el tiempo no tienen sentido. Los valores de la inversión que son inferiores al monto inicial de 10,000 dólares tampoco tienen sentido para una inversión que está aumentando de valor.
Por lo tanto, la función y la gráfica en lo que respecta a este problema relativo a las inversiones tiene
dominio\(y ≥ 10,000\) y rango\(t ≥ 0\).
La gráfica a continuación se restringe al dominio y rango que tengan sentido práctico para la inversión en este problema.