8.1: Espacios de muestreo y probabilidad
- Page ID
- 113737
En esta sección, aprenderás a:
- Escribir espacios de muestra.
- Calcular probabilidades examinando eventos simples en espacios de muestra.
Si se tiran dos monedas, ¿cuál es la probabilidad de que ambas monedas caigan cabezas? El problema parece bastante sencillo, pero no es raro escuchar la respuesta incorrecta 1/3. Un estudiante puede razonar incorrectamente que si se tiran dos monedas hay tres posibilidades, una cabeza, dos cabezas, o ninguna cabeza. Por lo tanto, la probabilidad de dos cabezas es una de cada tres. La respuesta es incorrecta porque si tiramos dos monedas hay cuatro posibilidades y no tres. Para mayor claridad, supongamos que una moneda es un centavo y la otra una moneda de níquel. Entonces tenemos las siguientes cuatro posibilidades.
HH HT TH TT
La posibilidad HT, por ejemplo, indica una cabeza en el centavo y una cola en el níquel, mientras que TH representa una cola en el centavo y una cabeza en el níquel. Es por esta razón, enfatizamos la necesidad de comprender los espacios muestrales.
Espacios de muestra
Un acto de voltear monedas, rodar dados, dibujar cartas o encuestar a personas se conoce como un experimento de probabilidad. Un espacio muestral de un experimento es el conjunto de todos los resultados posibles.
Si se enrolla una matriz, escriba un espacio de muestra.
Solución
Un dado tiene seis caras cada una con una probabilidad igual de probable de aparecer. Por lo tanto, el conjunto de todos los resultados posibles\(S\) es
{1, 2, 3, 4, 5, 6}.
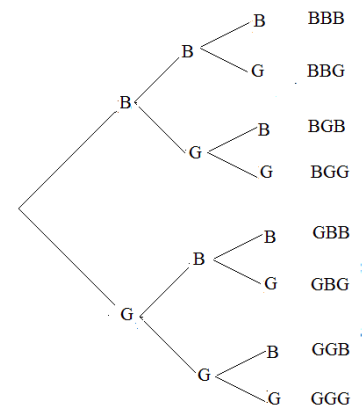
Una familia tiene tres hijos. Escribir un espacio de muestra.
Solución
El espacio muestral consta de ocho posibilidades.
{BBB, BBG, BGB, BGG, GBB, GBG, GGB, GGG}
La posibilidad BGB, por ejemplo, indica que el primogénito es un niño, el segundo nacido una niña, y el tercero un niño.
Ilustramos estas posibilidades con un diagrama de árbol.
Se rotan dos dados. Escriba el espacio de muestra.
Solución
Asumimos que uno de los dados es rojo, y el otro verde. Tenemos las siguientes 36 posibilidades.
| Verde | ||||||
| Rojo | 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | (1, 1) | (1, 2) | (1, 3) | (1, 4) | (1, 5) | (1, 6) |
| 2 | (2, 1) | (2, 2) | (2, 3) | (2, 4) | (2, 5) | (2, 6) |
| 3 | (3, 1) | (3, 2) | (3, 3) | (3, 4) | (3, 5) | (3, 6) |
| 4 | (4, 1) | (4, 2) | (4, 3) | (4, 4) | (4, 5) | (4, 6) |
| 5 | (5, 1) | (5, 2) | (5, 3) | (5, 4) | (5, 5) | (5, 6) |
| 6 | (6, 1) | (6, 2) | (6, 3) | (6, 4) | (6, 5) | (6, 6) |
La entrada (2, 5), por ejemplo, indica que el dado rojo muestra un 2, y el verde un 5.
Probabilidad
Ahora que entendemos el concepto de un espacio muestral, definiremos la probabilidad.
Para un espacio de muestra\(S\), y un resultado\(A\) de\(S\), se satisfacen las siguientes dos propiedades.
- Si\(A\) es un resultado de un espacio muestral, entonces la probabilidad de\(A\), denotada por\(P(A)\), está entre 0 y 1, inclusive. \[0 ≤ P(A) ≤ 1 \nonumber \]
- La suma de las probabilidades de todos los resultados en\(S\) igual a 1.
La probabilidad\(P(A)\) de un evento\(A\) describe la probabilidad o probabilidad de que ocurra ese evento.
- Si\(P(A) = 0\), el evento A es seguro que no ocurrirá. Si\(P(A) = 1\), el evento\(A\) es seguro que ocurrirá.
- Si\(P(A) = 0.5\), entonces el evento A es igualmente probable que ocurra o no ocurra.
- Si tiramos una moneda justa que es igualmente probable que aterrice sobre la cabeza o la cola, entonces P (Cabeza) = 0.50.
- Si el pronóstico del tiempo dice que hoy hay un 70% de probabilidad de lluvia, entonces P (Lluvia) = 0.70, lo que indica que es más probable que llueva que no llueva.
Si se tiran dos dados, uno rojo y otro verde, encuentra la probabilidad de que el dado rojo muestre un 3 y el verde muestre un seis.
Solución
Ya que se rodan dos dados, hay 36 posibilidades. La probabilidad de cada resultado, enumerado en Ejemplo\(\PageIndex{3}\), es igualmente probable.
Dado que (3, 6) es uno de esos resultados, la probabilidad de obtener (3, 6) es 1/36.
El ejemplo que acabamos de considerar consistió en un solo resultado del espacio muestral. A menudo nos interesa encontrar probabilidades de varios resultados representados por un evento.
Un evento es un subconjunto de un espacio de muestra. Si un evento consiste en un solo resultado, se llama un evento simple.
Si se tiran dos dados, encuentra la probabilidad de que la suma de las caras de los dados sea 7.
Solución
Que E represente el evento de que la suma de las caras de dos dados es 7.
Los casos posibles para que la suma sea igual a 7 son: (1, 6), (2,5), (3, 4), (4, 3), (5, 2)
y (6, 1), por lo que el evento E es
E = {(1, 6), (2,5), (3, 4), (4, 3), (5, 2), (6, 1)}
La probabilidad del evento E es
P (E) = 6/36 o 1/6.
Un frasco contiene 3 canicas rojas, 4 blancas y 3 azules. Si se elige una canica al azar, ¿cuál es la probabilidad de que la canica sea una canica roja o una canica azul?
Solución
Asumimos que las canicas son\(r_1\)\(r_2\),\(r_3\),\(w_1\),\(w_2\),\(w_3\),,\(w_4\),\(b_1\),\(b_2\),\(b_3\). Que el evento\(\mathrm{C}\) represente que el mármol es rojo o azul.
El espacio muestral\(\mathrm{S}=\left\{\mathrm{r}_{1}, \mathrm{r}_{2}, \mathrm{r}_{3}, \mathrm{w}_{1}, \mathrm{w}_{2}, \mathrm{w}_{3}, \mathrm{w}_{4}, \mathrm{b}_{1}, \mathrm{b}_{2}, \mathrm{b}_{3}\right\} \).
Y el evento\(\mathrm{C}=\left\{\mathrm{r}_{1}, \mathrm{r}_{2}, \mathrm{r}_{3}, \mathrm{b}_{1}, \mathrm{b}_{2}, \mathrm{b}_{3}\right\}\)
Por lo tanto, la probabilidad de\(\mathrm{C}\),
\[\mathrm{P}(\mathrm{C})=6 / 10 \text { or } 3 / 5 \nonumber \]
Un frasco contiene tres canicas numeradas 1, 2 y 3. Si se dibujan dos canicas sin reemplazo, ¿cuál es la probabilidad de que la suma de los números sea 5?
Nota: Las dos canicas de este ejemplo se dibujan consecutivamente sin reemplazo. Eso significa que después de dibujar una canica no se reemplaza en el frasco, y por lo tanto ya no está disponible para seleccionar en el segundo sorteo.
Solución
Dado que se dibujan dos canicas sin reemplazo, el espacio muestral consta de las siguientes seis posibilidades.
\[\mathrm{S}=\{(1,2),(1,3),(2,1),(2,3),(3,1),(3,2)\} \nonumber \]
Tenga en cuenta que (1,1), (2,2) y (3,3) no están listados en el espacio muestral. Estos resultados no son posibles al dibujar sin reemplazo, ya que una vez que se dibuja el primer mármol pero no se reemplaza en el frasco, ese mármol no está disponible en el frasco para ser seleccionado nuevamente en el segundo sorteo.
Que el evento\(\mathrm{E}\) represente que la suma de los números es cinco. Entonces
\[\mathrm{E}=\{(2,3),(3,2)\} \nonumber \]
Por lo tanto, la probabilidad de\(\mathrm{E}\) es
\[\mathrm{P}(\mathrm{E})=2 / 6 \text { or } 1 / 3 \nonumber. \nonumber \]
Un frasco contiene tres canicas numeradas 1, 2 y 3. Si se dibujan dos canicas sin reemplazo, ¿cuál es la probabilidad de que la suma de los números sea al menos 4?
Solución
El espacio muestral, como en Ejemplo\(\PageIndex{7}\), consta de las siguientes seis posibilidades.
\[\mathrm{S}=\{(1,2),(1,3),(2,1),(2,3),(3,1),(3,2)\} \nonumber \]
Que el evento\(\mathrm{F}\) represente que la suma de los números es de al menos cuatro. Entonces
\[\mathrm{F}=\{(1,3),(3,1),(2,3),(3,2)\} \nonumber \]
Por lo tanto, la probabilidad de\(\mathrm{F}\) es
\[\mathrm{P}(\mathrm{F})=4 / 6 \text { or } 2 / 3 \nonumber \]
Un frasco contiene tres canicas numeradas 1, 2 y 3. Si se dibujan dos canicas con reemplazo, ¿cuál es la probabilidad de que la suma de los números sea 5?
Nota: Las dos canicas de este ejemplo se dibujan consecutivamente con reemplazo. Eso significa que después de dibujar un mármol se reemplaza en el frasco, y por lo tanto está disponible para seleccionar nuevamente en el segundo sorteo.
Solución
Cuando se dibujan dos canicas con reemplazo, el espacio muestral consta de las siguientes nueve posibilidades.
\[\mathrm{S}=\{(1,1),(1,2),(1,3),(2,1),(2,2),(2,3),(3,1),(3,2),(3,3)\} \nonumber \]
Tenga en cuenta que (1,1), (2,2) y (3,3) se enumeran en el espacio muestral. Estos resultados son posibles al dibujar con reemplazo, ya que una vez que se dibuja y reemplaza el primer mármol, ese mármol no está disponible en el frasco para ser dibujado nuevamente.
Que el evento E represente que la suma de los números es cuatro. Entonces
\[ \mathrm{E} = {(2, 3), (3, 2) } \nonumber \]
Por lo tanto, la probabilidad de\(\mathrm{F}\) es\(\mathrm{P}(\mathrm{E}) = 2/9\)
Tenga en cuenta que en Ejemplo\(\PageIndex{9}\) cuando seleccionamos canicas con reemplazo, la probabilidad ha cambiado de Ejemplo\(\PageIndex{7}\) donde seleccionamos canicas sin reemplazo.
Un frasco contiene tres canicas numeradas 1, 2 y 3. Si se dibujan dos canicas con reemplazo, ¿cuál es la probabilidad de que la suma de los números sea al menos 4?
Solución
El espacio muestral al dibujar con reemplazo consta de las siguientes nueve posibilidades.
\[ \mathrm{S} = {(1,1), (1, 2), (1, 3), (2, 1), (2, 2), (2, 3), (3, 1), (3, 2), (3,3)} \nonumber \]
Que el evento\(\mathrm{F}\) represente que la suma de los números es de al menos cuatro. Entonces
\[ \mathrm{F} = {(1, 3), (3, 1), (2, 3), (3, 2), (2,2), (3,3)} \nonumber \]
Por lo tanto, la probabilidad de\(\mathrm{F}\) es
\[\mathrm{P}(\mathrm{F}) = 6/9 \text{ or } 2/3 \nonumber. \nonumber \]
Tenga en cuenta que en Ejemplo\(\PageIndex{10}\) cuando seleccionamos canicas con reemplazo, la probabilidad es la misma que en Ejemplo\(\PageIndex{8}\) donde seleccionamos canicas sin reemplazo.
Así, el muestreo con o sin reemplazo PUEDE cambiar las probabilidades, pero no, dependiendo de la situación en el problema particular que se esté considerando. Reexaminaremos los conceptos de muestreo con y sin reemplazo en la Sección 8.3.
Un troquel de 6 lados se enrolla una vez. Encuentra la probabilidad de que el resultado sea mayor a 4.
Solución
El espacio muestral consta de las siguientes seis posibilidades en conjunto\(\mathrm{S}\):\(\mathrm{S}={1,2,3,4,5,6}\)
\(\mathrm{E}\)Sea el evento de que el número rodado sea mayor a cuatro:\(\mathrm{E}={5,6} \)
Por lo tanto, la probabilidad de\(\mathrm{E}\) es:\(\mathrm{P}(\mathrm{E}) = 2/6 \text{ or } 1/3\).