9.1: Probabilidad binomial

Última actualización
Guardar como PDF

Page ID: 113886

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de aprendizaje

En esta sección, aprenderás a:

Reconocer cuándo usar la distribución binomial de probabilidad
Derivar la fórmula para la distribución binomial de probabilidad
Calcular probabilidades para un experimento de probabilidad binomial

En esta sección, consideramos problemas que involucran una secuencia de ensayos, donde cada ensayo tiene sólo dos resultados, un éxito o un fracaso. Estos juicios son independientes, es decir, el resultado de uno no afecta el resultado de ningún otro juicio. La probabilidad de éxito$p$, y la probabilidad de fracaso$(1 - p)$, siguen siendo las mismas a lo largo del experimento. Estos problemas se denominan problemas binomiales de probabilidad. Dado que estos problemas fueron investigados por el matemático suizo Jacques Bernoulli alrededor de 1700, también se les llama ensayos de Bernoulli.

Damos la siguiente definición:

Experimento binomial

Un experimento binomial satisface las siguientes cuatro condiciones:

Solo hay dos resultados, un éxito o un fracaso, para cada ensayo.
El mismo experimento se repite varias veces.
Los juicios son independientes; es decir, el resultado de un juicio en particular no afecta el resultado de ningún otro juicio.
La probabilidad de éxito sigue siendo la misma para cada ensayo.

Este modelo de probabilidad que nos dará las herramientas para resolver muchos problemas de la vida real, tales como:

Si una moneda es volteada 10 veces, ¿cuál es la probabilidad de que caiga cabezas 3 veces?
Si un basquetbolista hace 3 de cada 4 tiros libres, ¿cuál es la probabilidad de que haga 7 de 10 tiros libres en un juego?
Si un medicamento cura al 80% de las personas que lo toman, ¿cuál es la probabilidad de que entre las diez personas que toman el medicamento, 6 se curen?
Si un fabricante de microchips afirma que solo 4% de sus chips son defectuosos, ¿cuál es la probabilidad de que entre los 60 chips elegidos, exactamente tres sean defectuosos?
Si un ejecutivo de telemarketing ha determinado que 15% de las personas contactadas comprarán el producto, ¿cuál es la probabilidad de que entre las 12 personas que son contactadas, 2 compren el producto?

Consideramos ahora el siguiente ejemplo para desarrollar una fórmula para encontrar la probabilidad de$k$ éxitos en los ensayos de$n$ Bernoulli.

Ejemplo$\PageIndex{1}$

Un beisbolista tiene un promedio de bateo de .300. Si bate cuatro veces en un juego, encuentra la probabilidad de que tenga

4 hits
3 hits
2 hits
1 hit
sin aciertos.

Solución

Que S denote que el jugador recibe un hit, y F denota que no recibe un hit.

Este es un experimento binomial porque cumple las cuatro condiciones. Primero, solo hay dos resultados, S o F. Claramente el experimento se repite cuatro veces. Por último, si asumimos que la habilidad del jugador para obtener un hit no cambia cada vez que llega al bate, las pruebas son independientes con una probabilidad de .3 de obtener un hit durante cada prueba.

Dibujamos un diagrama de árbol para mostrar todas las situaciones.

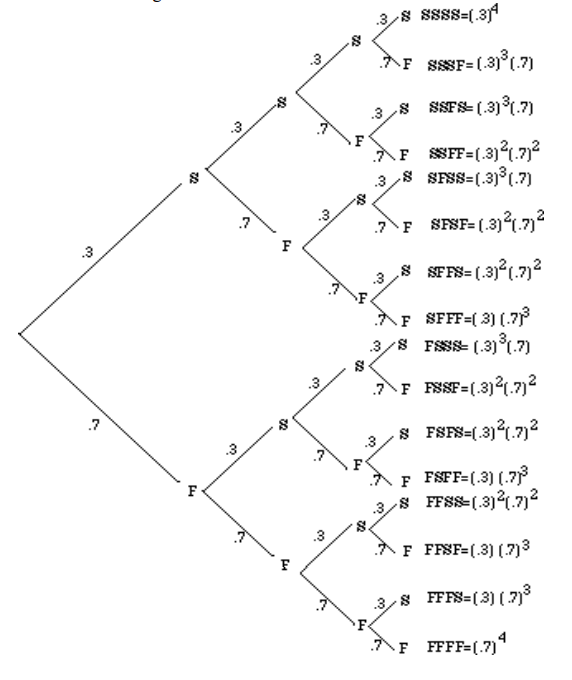
$Ejemplo9.1.1.png$

Primero encontremos la probabilidad de conseguir, por ejemplo, dos hits. Habrá que considerar las seis posibilidades, SSFF, SFSF, SFFS, FSSF, FSFS, FFSS, como se muestra en el diagrama de árbol anterior. A continuación enumeramos las probabilidades de cada uno.

\ [\ begin {array} {l}
\ mathrm {P} (\ mathrm {SSFF}) =( .3) (.3) (.7) (.7) = (.3) ^ {2} (.7) ^ {2}\
\ mathrm {P} (\ mathrm {SFSF}) =( .3) (.7) (.3) =( .3) ^ {2} (.7) ^ {2}\\\ mathrm {P} (
\ mathrm {SFFS}) =( .3) (.7) (.7) (.3) =( .3) ^ {2} (.7) ^ {2}\\ mathrm {P} (
\ mathrm {FSSF}) =( .7) (.3) (.3) (.7) =( .3) =( .3) =( .3) ) ^ {2} (.7) ^ {2}\\
\ mathrm {P} (\ mathrm {FSFS}) =( .7) (.3) (.7) (.3) = (.3) ^ {2} (.7) ^ {2}
\\ mathrm {P} (\ mathrm {FFSS}) =( .7) (.7) (.3) =( .3) ^ {2} (.7) ^ {2}
\ end {array}\ nonumber\]

Dado que la probabilidad de cada uno de estos seis resultados es$(.3)^2(.7)^2$, la probabilidad de obtener dos éxitos es$6(.3)^2(.7)^2$.

La probabilidad de obtener un golpe se puede obtener de la misma manera. Dado que cada permutación tiene una S y tres F, hay cuatro resultados de este tipo: SFFF, FSFF, FFSF y FFFS.

Y como la probabilidad de cada uno de los cuatro resultados es$(.3)(.7)^3$, la probabilidad de obtener un hit es$4(.3)(.7)^3$.

La siguiente tabla enumera las probabilidades para todos los casos, y muestra una comparación con la expansión binomial de cuarto grado. Nuevamente,$p$ denota la probabilidad de éxito, y$q = (1 - p)$ la probabilidad de fracaso.

Resultado	Cuatro Éxitos	Tres Éxitos	Dos Éxitos	Un golpe	Sin Éxitos
Probabilidad	$(.3)^4$	$4 (.3)^3(.7)$	$6 (.3)^2(.7)^2$	$4 (.3)(.7)^3$	$(.7)^4$

\ [\ begin {array} {l}
(.3+.7) ^ {4} = (.3) ^ {4} +4 (.3) ^ {3} (.7) +6 (.3) ^ {2} (.7) ^ {2} +4 (.3) (.7) ^ {3} + (.7) ^ {4}\
(p+q) ^ {4} =p^ {4} =p^ {4} +4 p^ {3} q+6 p^ {2} q^ {2} +4 p q^ {3} +q^ {4}
\ end {array}\ nonumber\]

Esto nos da el siguiente teorema:

Teorema de Probabilidad Binomial

La probabilidad de obtener$k$ éxitos en ensayos$n$ independientes de Bernoulli viene dada por

\[ \mathbf{P}(\mathbf{n}, \mathbf{k} ; \mathbf{p})=\mathbf{n} \mathbf{C} \mathbf{k} \: \mathbf{p}^{\mathbf{k}} \mathbf{q}^{\mathbf{n}-\mathbf{k}} \nonumber \]

donde$p$ denota la probabilidad de éxito y$q = (1 - p) $ la probabilidad de fracaso.

Utilizamos la fórmula de probabilidad binomial para resolver los siguientes ejemplos.

Ejemplo$\PageIndex{2}$

Si una moneda es volteada 10 veces, ¿cuál es la probabilidad de que caiga cabezas 3 veces?

Solución

Que S denote la probabilidad de obtener una cabeza, y F la probabilidad de obtener una cola.

Claramente$n = 10$,$k = 3$,,$p = 1/2$, y$q = 1/2$.

Por lo tanto,$\mathrm{b}(10,3 ; 1 / 2)=10 \mathrm{C} 3 \: (1 / 2)^{3}(1 / 2)^{7}=.1172$

Ejemplo$\PageIndex{3}$

Si un basquetbolista hace 3 de cada 4 tiros libres, ¿cuál es la probabilidad de que logre 6 de 10 tiros libres en un juego?

Solución

La probabilidad de hacer un tiro libre es de 3/4.
Por lo tanto$p = 3/4$,$q = 1/4$,$n = 10$,, y$k = 6$.

Por lo tanto,$b(10, 6; 3/4) = 10\mathrm{C}6 \: (3/4)^6(1/4)^4 = .1460$

Ejemplo$\PageIndex{4}$

Si un medicamento cura al 80% de las personas que lo toman, ¿cuál es la probabilidad de que de las ocho personas que toman el medicamento, 5 se curen?

Solución

Aquí$p =.80$,$q = .20$,$n = 8$, y$k = 5$.

\[ b(8, 5; .80) = 8\mathrm{C}5 \: (.80)^5(.20)^3 = .1468 \nonumber \]

Ejemplo$\PageIndex{5}$

Si un fabricante de microchips afirma que solo 4% de sus chips son defectuosos, ¿cuál es la probabilidad de que entre los 60 chips elegidos, exactamente tres sean defectuosos?

Solución

Si S denota la probabilidad de que el chip esté defectuoso, y F la probabilidad de que el chip no esté defectuoso$p = .04$, entonces$q = .96$,$n = 60$, y$k = 3$.

\[ b(60, 3; .04) = 60 \mathrm{C} 3 \: (.04)^3(.96)^{57} = .2138 \nonumber \]

Ejemplo$\PageIndex{6}$

Un ejecutivo de telemarketing ha determinado que 15% de las personas contactadas comprarán el producto. Se contacta a 12 personas sobre este producto.

Encuentra la probabilidad de que entre 12 personas contactadas, 2 compren el producto.
Encuentra la probabilidad de que entre 12 personas contactadas, a lo sumo 2 compren el producto?

Solución

a. si S denota la probabilidad de que una persona compre el producto, y F la probabilidad de que la persona no compre el producto, entonces$p = .15$,$q = .85$,$n = 12$, y$k = 2$.

\[b(12, 2; .15) = 12 \mathrm{C} 2 \: (.15)^2(.85)^{10} = .2924 \nonumber. \nonumber \]

La probabilidad de que 2 personas compren el producto es de 0.2924.

b. nuevamente$p = .15$,$q = .85$,$n = 12$. Pero para encontrar la probabilidad de que a lo sumo 2 compren el producto, necesitamos encontrar las probabilidades para$k= 0$,$k=1$,$k=2$ y sumarlas juntas.

\ [\ begin {array} {l}
\ mathrm {b} (12,0; .15) =12\ mathrm {C} 0\: (.15) ^ {0} (.85) ^ {12} =.1422\
\ mathrm {b} (12,1; .15) =12\ mathrm {C} 1\: (.15) ^ {1} (.85) ^ {11} =.3012
\ end {array}\ nonumber\]

Sumando las tres probabilidades da: .1422 +0.3012 +.2924 = .7358

La probabilidad de que como máximo 2 personas compren el producto es de 0.7358.

Objetivos de aprendizaje

Experimento binomial

Ejemplo\(\PageIndex{1}\)

Teorema de Probabilidad Binomial

Ejemplo\(\PageIndex{2}\)

Ejemplo\(\PageIndex{3}\)

Ejemplo\(\PageIndex{4}\)

Ejemplo\(\PageIndex{5}\)

Ejemplo\(\PageIndex{6}\)