9.4: Probabilidad usando diagramas de árbol

Última actualización
Guardar como PDF

Page ID: 113887

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de aprendizaje

En esta sección, aprenderás a:

Usar árboles de probabilidad para organizar la información en problemas de probabilidad
Usar árboles de probabilidad para calcular probabilidades

Como ya hemos visto, los diagramas de árbol juegan un papel importante en la resolución de problemas de probabilidad. Un diagrama de árbol nos ayuda no solo a visualizar, sino también a enumerar todos los resultados posibles de manera sistemática. Además, cuando enumeramos varios resultados de un experimento y sus probabilidades correspondientes en un diagrama de árbol, obtenemos una mejor comprensión de cuándo se multiplican las probabilidades y cuándo se agregan.

Los significados de las palabras y y o se aclaran cuando aprendemos a multiplicar las probabilidades horizontalmente a través de las ramas, y agregar probabilidades verticalmente hacia abajo del árbol.

Aunque los diagramas de árbol no son prácticos en situaciones en las que los posibles resultados se vuelven grandes, son una herramienta importante para desglosar el problema de manera esquemática. Consideramos algunos ejemplos que pueden parecer difíciles al principio, pero con la ayuda de un diagrama de árbol, se pueden resolver fácilmente.

Ejemplo$\PageIndex{1}$

Una persona tiene cuatro llaves y sólo una llave cabe a la cerradura de una puerta. ¿Cuál es la probabilidad de que la puerta cerrada se pueda desbloquear en como máximo tres intentos?

Solución

Que U sea el evento de que la puerta haya sido desbloqueada y L sea el evento de que la puerta no haya sido desbloqueada. Ilustramos con un diagrama de árbol.

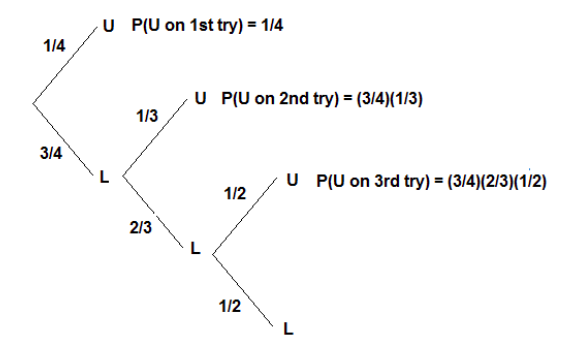
$Ejemplo9.4.1.png$

La probabilidad de desbloquear la puerta en el primer intento = 1/4

La probabilidad de desbloquear la puerta en el segundo intento = (3/4) (1/3) = 1/4

La probabilidad de desbloquear la puerta en el tercer intento = (3/4) (2/3) (1/2) = 1/4

Por lo tanto, la probabilidad de desbloquear la puerta en como máximo tres intentos = 1/4 + 1/4 + 1/4 = 3/4.

Ejemplo$\PageIndex{2}$

Un frasco contiene 3 mármoles negros y 2 blancos. Seguimos dibujando canicas una a la vez hasta que se dibujan dos canicas negras. Si se dibuja un mármol blanco, se registra el resultado y el mármol se vuelve a poner en el frasco antes de dibujar el siguiente mármol. ¿Cuál es la probabilidad de que obtengamos exactamente dos canicas negras en como máximo tres intentos?

Solución

Ilustramos usando un diagrama de árbol.

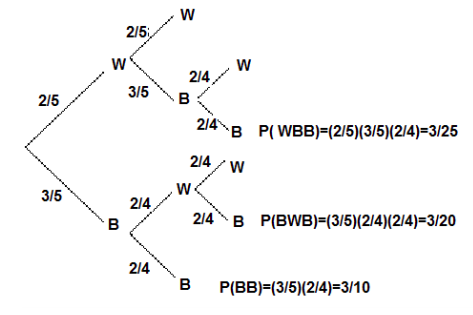
$Ejemplo9.4.2.png$

La probabilidad de que obtengamos dos canicas negras en los dos primeros intentos se enumera adyacente a la rama más baja, y es = 3/10.

La probabilidad de obtener primero negro, segundo blanco y tercer negro = 3/20.

De igual manera, la probabilidad de obtener primero blanco, segundo negro y tercer negro = 3/25.

Por lo tanto, la probabilidad de obtener exactamente dos canicas negras en como máximo tres intentos = 3/10 + 3/20 + 3/25 = 57/100.

Ejemplo$\PageIndex{3}$

Un circuito consta de tres resistencias: resistencia$R_1$$R_2$, resistencia y resistencia$R_3$, unidas en serie. Si una de las resistencias falla, el circuito deja de funcionar. Las probabilidades de que las resistencias$R_1$,$R_2$, o$R_3$ vayan a fallar son. 07,. 10, y. 08, respectivamente. ¿Encuentra la probabilidad de que al menos una de las resistencias falle?

Solución

La probabilidad de que al menos una de las resistencias falle = 1 - ninguna de las resistencias falla.

Es bastante fácil encontrar la probabilidad del suceso de que ninguna de las resistencias falle.
Ni siquiera necesitamos dibujar un árbol porque podemos visualizar la única rama del árbol que asegura este desenlace.

Las probabilidades de que$R_1$,$R_2$,$R_3$ no falle son. 93,. 90, y. 92 respectivamente. Por lo tanto, la probabilidad de que ninguna de las resistencias falle = (. 93) (. 90) (. 92) =. 77.

Así, la probabilidad de que al menos uno de ellos falle = 1 -. 77 =. 23.

Objetivos de aprendizaje

Ejemplo\(\PageIndex{1}\)

Ejemplo\(\PageIndex{2}\)

Ejemplo\(\PageIndex{3}\)