Search

Text Color

Margin Size

Font Type

Enable Dyslexic Font

1.6: Precisión y GPE

Última actualización

30 oct 2022
Guardar como PDF
- 1.5: Precisión y cifras significativas
- 1.7: Fórmulas

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

Precisión

La precisión de un número es el valor posicionar de la cifra significativa más a la derecha. Por ejemplo, $100.45$ es preciso al lugar de las centésimas, y $3,840$ es preciso al lugar de las decenas.

Ejercicios $\PageIndex{1}$

Identificar la precisión (es decir, el valor posicionar de la cifra significativa más a la derecha) de cada número.

1. $63,400$

2. $63,040$

3. $63,004$

4. $8,000$

5. $8,\overline{0}00$

6. $8,0\overline{0}0$

7. $8,00\overline{0}$

8. $0.085$

9. $0.0805$

10. $0.08050$

Responder

1. cientos

2. decenas

3. los

4. miles

5. cientos

6. decenas

7. unos

8. milésimas

9. diez milésimas

10. cien milésimas

Redondeo basado en precisión

En un módulo anterior sobre decimales, utilizamos redondeo basado en precisión porque estábamos redondeando a un valor positorio especificado; por ejemplo, redondeo a la décima más cercana. Practicemos esto con barras superiores y ceros al final.

Redondeo basado en precisión:

Localice el dígito de redondeo en el lugar al que esté redondeando.
Mire el dígito de prueba directamente a la derecha del dígito de redondeo.
Si el dígito de prueba es 5 o mayor, aumente el dígito de redondeo en 1 y deje caer todos los dígitos a su derecha. Si el dígito de prueba es menor que 5, mantenga el dígito de redondeo igual y baje todos los dígitos a su derecha.

Recuerda, cuando el dígito de redondeo de un número entero es a $9$ que se redondea hacia arriba a a $0$ , debemos escribir una barra superior por encima de eso $0$ .

Además, cuando el dígito de redondeo de un número decimal es a $9$ que se redondea hacia arriba a a $0$ , debemos incluir el $0$ en esa posición decimal.

Ejercicios $\PageIndex{1}$

Redondea cada número al valor posicionar indicado. Asegúrese de incluir ceros a la izquierda o una barra superior si es necesario.

11. $13,997$ (miles)

12. $13,997$ (cientos)

13. $13,997$ (decenas)

14. $0.5996$ (décimas)

15. $0.5996$ (centésimas)

16. $0.5996$ (milésimas)

Responder

11. $14,000$

12. $14,\overline{0}00$

13. $14,0\overline{0}0$

14. $0.6$

15. $0.60$

16. $0.600$

Precisión al sumar y restar

Supongamos que la asistencia a un evento grande se estima en $25,000$ personas, pero luego ves que la $3$ gente se va. ¿Es la nueva estimación $24,997$ ? No, porque la estimación original era precisa sólo al mil más cercano. No podemos comenzar con un número impreciso y terminar con un número más preciso. Si estimamos que la $1,000$ gente se había ido, entonces podríamos revisar nuestra estimación de asistencia $24,000$ porque esta estimación mantiene el mismo nivel de precisión que nuestra estimación original.

Al sumar o restar números con diferentes niveles de precisión, la respuesta debe redondearse con la misma precisión que la menos precisa de los números originales.

No redondee los números originales; primero haga los cálculos necesarios, luego redondee la respuesta como último paso.

Ejercicios $\PageIndex{1}$

Sumar o restar como se indica. Redondear al nivel apropiado de precisión.

17. Encuentre el peso combinado de cuatro paquetes con los siguientes pesos: $9.7$ lb, $13$ lb, $10.5$ lb, $6.1$ lb.

18. Encuentre el peso combinado de cuatro paquetes con los siguientes pesos: $9.7$ lb, $13.0$ lb, $10.5$ lb, $6.1$ lb.

19. Al comprar un seguro de inquilinos, Chandra estima el valor de sus posesiones asegurables en $ $10,200$ . Después de vender algunos artículos valorados en $ $375$ , ¿cuál sería la estimación revisada?

20. Chandra sabe que tiene aproximadamente $ $840$ en su cuenta corriente. Después de usar su tarjeta de débito para realizar dos compras de $ $25.95$ y $ $16.38$ , ¿cuánto le quedaría en su cuenta?

Responder

17. $39$ lb

18. $39.3$ lb

19. $ $9,800$

20. $ $8\overline{0}0$

Si estás multiplicando por un número exacto, puedes considerar esto como una adición repetida. Por ejemplo, supongamos que mide el peso de un objeto para ser $4.37$ onzas y quiere saber el peso de tres de estos objetos; multiplicar $4.37$ tiempos $3$ es lo mismo que agregar $4.37 + 4.37 + 4.37 = 13.11$ onzas. La precisión aún está al lugar de las centésimas. El tema de las cifras significativas no se aplica a los números exactos, por lo que sería erróneo tratar $3$ como tener solo una sig fig. (Trate a los números exactos como realeza; su precisión es perfecta y sería un insulto incluso cuestionarlo).

Mayor error de medición posible (GPE)

Supongamos que está pesando a un perro con una báscula que muestra el peso redondeado a la libra más cercana. Si la báscula dice que Sir Barks-A-Lot pesa $23$ libras, podría pesar en cualquier lugar desde $22.5$ libras hasta casi $23.5$ libras. El peso verdadero podría ser tanto como $0.5$ libras por encima o por debajo del peso medido, que podríamos escribir como $23\pm0.5$ .

Ahora suponga que está pesando a Sir Barks-A-Lot con una báscula que muestra el peso redondeado al décimo de libra más cercano. Si la báscula dice que Sir Barks-A-Lot pesa $23.0$ libras, ahora sabemos que podría pesar en cualquier lugar desde $22.95$ libras hasta casi $23.05$ libras. El peso verdadero podría ser tanto como $0.05$ libras por encima o por debajo del peso medido, que podríamos escribir como $23.0\pm0.05$ .

A medida que aumentamos el nivel de precisión en nuestra medición, disminuimos el mayor error de medición posible o GPE. El GPE es siempre la mitad de la precisión; si la precisión es a la décima más cercana, $0.1$ , el GPE es la mitad de una décima, o cinco centésimas, $0.05$ . El GPE siempre estará $5$ en el lugar a la derecha del valor positorio de la precisión del número.

Otra forma de pensar sobre el GPE es que da el rango de valores que redondearían al número en cuestión. Volver al pesaje de Sir Barks-A-Lot: nos $23\pm0.5$ dice un valor inferior y un valor superior. $23-0.5=22.5$ es el peso más bajo que redondearía hasta $23$ . De igual manera, $23+0.5=23.5$ es el peso más alto que redondearía a la baja $23$ . Sí, tal vez deberíamos decir $23.49$ o $23.499$ , etc., para el límite superior aquí, pero es más fácil simplemente decir $23.5$ y estar de acuerdo que $23.5$ es el límite superior aunque redondearía hacia arriba en lugar de hacia abajo. Usando desigualdades, podríamos representar $23\pm0.5$ como el rango de valores $22.5\leq\text{weight}<23.5$ en su lugar.

Cuando se le pide que identifique el GPE, puede ayudar pensar “¿Cuáles son los números mínimos y máximos que redondearían al número dado?” Por ejemplo, supongamos que se estima que la asistencia a un partido de Portland Thorns es de $14,000$ personas. Este número es preciso al mil más cercano. El número mínimo que redondearía a $14,000$ sería $13,500$ (porque $13,449$ redondearía hacia abajo a $13,000$ ), y el número máximo que redondearía a la baja $14,000$ estaría justo por debajo $14,500$ (porque $14,500$ redondearía hasta $15,000$ ). Debido a que estos números están cada uno $500$ lejos de $14,000$ , el GPE es $500$ . Si la estimación de $14,000$ es correcta al mil más cercano, sabemos que la asistencia real está dentro de los $\pm$ 500 de $14,000$ .

Ejercicios $\PageIndex{1}$

21. Un paquete pesa $3.76$ libras. ¿Qué es el GPE?

22. Un rollo de lámina de plástico tiene $0.00031$ pulgadas de grosor. ¿Qué es el GPE en pulgadas?

23. Láminas de plástico $0.00031$ pulgadas de espesor se conoce como $0.31$ mil. ¿Qué es el GPE en mils?

Responder

21. $\pm 0.005$ lb

22. $\pm 0.000005$ en

23. $\pm 0.005$ mil

Recordemos del módulo anterior que la precisión de una medición es el número de cifras significativas. Reunamos las ideas de precisión, precisión y mayor error de medición posible.

Ejercicios $\PageIndex{1}$

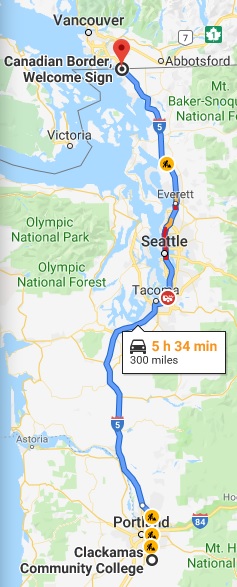
$Mapa de Google que muestra una ruta de 300 millas desde Clackamas Community College al norte hasta la frontera canadiense$

Google Maps dice que la distancia en automóvil desde el campus principal de CCC hasta la frontera canadiense es de $300$ millas. (Nota: esto se redondea a la milla más cercana.)

24. ¿Cuál es la precisión?

25. ¿Cuál es la precisión?

26. ¿Qué es el GPE?

Se espera que un nuevo estadio tenga alrededor de $23,000$ asientos.

27. ¿Cuál es la precisión?

28. ¿Cuál es la precisión?

29. ¿Qué es el GPE?

La capacidad del tanque de gasolina de un automóvil es de $14.2$ galones.

30. ¿Cuál es la precisión?

31. ¿Cuál es la precisión?

32. ¿Qué es el GPE?

Responder

24. tres cifras significativas

25. el lugar de los unos; la $1$ milla más cercana

26. $\pm 0.5$ mi

27. dos cifras significativas

28. miles de lugares; los $1,000$ asientos más cercanos

29. $\pm 500$ asientos

30. tres cifras significativas

31. décimos lugar; el $0.1$ galón más cercano

32. $\pm 0.05$ gal

Aquí un resumen de los términos importantes de estos dos módulos. Es fácil mezclarlos, pero recordar que la “precisión” y el “valor posicionar” ambos comienzan con “p” puede ser útil.

Resumen de Términos

Cifras significativas: los dígitos en un número que confiamos para ser correctos

Precisión: el número de dígitos significativos

Precisión: el valor posicionar del dígito significativo más a la derecha

Mayor error de medición posible (GPE): la mitad de la precisión

Precisión

Ejercicios1.6.1\PageIndex{1}

Redondeo basado en precisión

Ejercicios1.6.1\PageIndex{1}

Precisión al sumar y restar

Ejercicios1.6.1\PageIndex{1}

Mayor error de medición posible (GPE)

Ejercicios1.6.1\PageIndex{1}

Ejercicios1.6.1\PageIndex{1}

Resumen de Términos

Support Center

How can we help?

Ejercicios $\PageIndex{1}$

Ejercicios $\PageIndex{1}$

Ejercicios $\PageIndex{1}$

Ejercicios $\PageIndex{1}$

Ejercicios $\PageIndex{1}$