1.7: Fórmulas
- Page ID
- 110936
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Puede usar una calculadora a lo largo de este módulo si es necesario.
Fórmulas
Una fórmula es una ecuación o conjunto de cálculos que toma un número (o números) como entrada y produce una salida. La salida suele ser un número, pero también podría ser una decisión como sí o no. Los números en una fórmula generalmente se representan con letras del alfabeto, las cuales se llaman variables porque sus valores pueden variar. Para evaluar una fórmula, sustituimos un número (o números) en la fórmula y luego realizamos los pasos usando el orden de las operaciones.
Nota: Cuando se escribe un número directamente junto a una variable, indica multiplicación. Por ejemplo,\(2H\) significa\(2\cdot{H}\).
El costo, en dólares, de enviar un sobre grande que pese\(w\) onzas se calcula mediante la fórmula\(C=0.20w+0.80\). [1]
1. Encuentre el costo de enviar un sobre de\(3\) -onza.
2. Encuentre el costo de enviar un sobre de\(9\) -onza.
Radio Cab cobra las siguientes tarifas por un viaje en taxi: una tarifa fija de $\(3.50\) más una tarifa de $\(2.60\) por milla. El costo total, en dólares, de un viaje de\(m\) millas de largo puede ser representado por la fórmula\(C=3.50+2.60m\). [2]
3. Encuentra el costo de un viaje de\(5\) -milla.
4. Encuentra el costo de un viaje de\(7.5\) -milla.
5. Encuentra el costo de subirte al taxi, luego cambiar de opinión y salir sin viajar a ningún lado.
El número de miembros que tiene un estado en la Cámara de Representantes de Estados Unidos se puede aproximar por la fórmula\(R=P\div{.7}\), [3] donde\(P\) está la población en millones. Las poblaciones de 2010 de tres estados son las siguientes: [4]
| Oregon | \(3.8\text{ million}\) |
| Washington | \(6.7\text{ million}\) |
| California | \(37.2\text{ million}\) |
Redondea todas las respuestas al número entero más cercano.
6. ¿Cuántos Representantes de Estados Unidos tiene Oregon?
7. ¿Cuántos Representantes de Estados Unidos tiene Washington?
8. ¿Cuántos Representantes de Estados Unidos tiene California?
El número de votos electorales que tiene un estado se puede aproximar por la fórmula\(E=P\div{0.7}+2\), donde\(P\) está la población en millones.
9. ¿Cuántos votos electorales tiene Oregon?
10. ¿Cuántos votos electorales tiene Washington?
11. ¿Cuántos votos electorales tiene California?
- Contestar
-
1. $\(1.40\)
2. $\(2.60\)
3. $\(16.50\)
4. $\(23.00\)
5. $\(3.50\)
6. \(5\)representantes (redondeado a partir de\(5.43\))
7. \(10\)representantes (redondeados de\(9.57\))
8. \(53\)representantes (redondeado a partir de\(53.14\))
9. \(7\)votos electorales
10. \(12\)votos electorales
11. \(55\)votos electorales
Algunas fórmulas requieren más de un número para la entrada.
Cuando se revisa la presión arterial de un paciente, generalmente se le indican dos números: la presión arterial sistólica (PAS) y la presión arterial diastólica (DBP). La presión arterial media (MAP) puede estimarse mediante la siguiente fórmula:\(MAP=\dfrac{SBP+2\cdot{DBP}}{3}\). (Las unidades son mm Hg, o milímetros de mercurio). Calcular la presión arterial media para cada paciente.
12. SBP =\(120\), DBP =\(75\)
13. SBP =\(140\), DBP =\(90\)
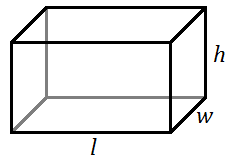UPS utiliza esta fórmula para determinar la “medición” de un paquete con longitud\(l\)\(w\), ancho y altura\(h\):\(m=l+2w+2h\). [5] Determinar la medida de un paquete con las siguientes dimensiones.
14. largo\(18\) pulgadas, ancho\(12\) pulgadas, alto\(14\) pulgadas
15. largo\(16\) pulgadas, ancho\(14\) pulgadas, alto\(15\) pulgadas
- Responder
-
12. \(90\)mm Hg
13. alrededor\(107\) mm Hg
14. \(70\)en
15. \(74\)en
El siguiente conjunto de ejercicios implica una fórmula que da una respuesta de sí o no.
En Australia, un huevo de gallina se designa “grande” si su masa, en gramos, satisface la siguiente fórmula:\(|m-54.1|\leq4.1\). Determinar si cada huevo califica como grande. [6]
16. La masa del huevo 1 es\(57.8\) gramos.
17. La masa del huevo 2 es\(58.3\) gramos.
18. La masa del huevo 3 es\(49.8\) gramos.
19. La masa del huevo 4 es\(50.0\) gramos.
- Responder
-
16. si
17. no; demasiado grande
18. no; demasiado pequeño
19. si
Temperatura
La escala de temperatura Celsius se basa en el punto de congelación del agua (\(0\)°C =\(32\) °F) y el punto de ebullición del agua (\(100\)°C =\(212\) °F). Al restar estos números, podemos ver que una diferencia de\(180\) °F es equivalente a\(100\) °C. La relación se\(\dfrac{180}{100}\) reduce a\(\dfrac{9}{5}\), lo que significa que\(9\) grados en la escala Fahrenheit es equivalente a\(5\) grados en la escala Celsius. (Por supuesto, también\(\dfrac{180}{100}\) es igual a\(1.8\), lo que significa que el\(1\) grado Celsius es equivalente a\(1.8\) grados Fahrenheit.) Debido a que Fahrenheit y Celsius no tienen el mismo punto cero, sin embargo, debemos sumar o restar\(32\) también. Consulte las fórmulas a continuación.
Fórmulas de temperatura
\(F=\dfrac{9}{5}C+32\)o\(F=1.8C+32\)
\(C=\dfrac{5}{9}(F-32)\)o\(C=(F-32)\div{1.8}\)
20. La temperatura en un día frío es de\(10\) °C. Convierte esta temperatura a Fahrenheit.
21. La temperatura corporal normal es de\(98.6\) °F. ¿Cuál es esta temperatura en Celsius?
22. La FDA recomienda que un congelador se establezca por debajo de\(-18\) °C. ¿Cuál es el equivalente Fahrenheit?
23. Un paquete de panqueques congelados de IKEA exige que el horno se ajuste a\(392\) °F Claramente, esto se calculó originalmente en grados centígrados. ¿Cuál es la temperatura Celsius correspondiente?
- Responder
-
20. \(50\)°C
21. \(37\)°C
22. \(-0.4\)°F
23. \(200\)°C
- Pe.usps.com/text/dmm300/notice123.htm #_c037
- [1]https://www.radiocab.net/services-radio-cab/
- [2]https://www.pewresearch.org/fact-tank/2018/05/31/u-s-population-keeps-growing-but-house-of-representatives-is-same-size-as-in-taft-era/
- [3]https://en.Wikipedia.org/wiki/List_of_states_and_territories_of_the_United_States_by_population
- www.ups.com/us/es/help-center/embalaje-y-suministros/prepare-overize.page
- [4]https://en.Wikipedia.org/wiki/Chicken_egg_sizes