1.3: Geometría

Última actualización
Guardar como PDF

Page ID: 112943

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Las formas geométricas, así como el área y los volúmenes, a menudo pueden ser importantes en la resolución de problemas.

Ejemplo$\PageIndex{1}$

Tienes curiosidad por lo alto que es un árbol, pero no tienes forma de treparlo. Describir un método para determinar la altura.

Solución

Hay varios enfoques que podríamos tomar. Usaremos uno basado en triángulos, lo que requiere que sea un día soleado. Supongamos que el árbol está proyectando una sombra, digamos 15 pies de largo. Entonces puedo hacer que un amigo me ayude a medir mi propia sombra. Supongamos que tengo 6 pies de altura y arrojo una sombra de 1.5 pies. Dado que el triángulo formado por el árbol y su sombra tiene los mismos ángulos que el triángulo formado por mí y mi sombra, estos triángulos se llaman triángulos similares y sus lados escalarán proporcionalmente. Es decir, la relación entre la altura y la anchura será la misma en ambos triángulos. Usando esto, podemos encontrar la altura del árbol, que denotaremos por$h$:

\[ \dfrac{6 \text{ ft tall}}{1.5 \text{ ft shadow}} = \dfrac{h \text{ ft tall}}{15 \text{ ft shadow}} \nonumber \]

Multiplicando ambos lados por 15, obtenemos$h$ = 60. El árbol mide aproximadamente 60 pies de altura.

Puede ser útil recordar algunas fórmulas para áreas y volúmenes de algunas formas básicas.

Definición: Áreas

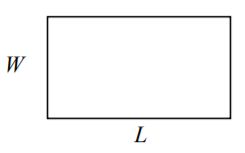
Rectángulo

Área:$L \cdot W$

Perímetro:$2L + 2W$

$clipboard_e5d5868122c3c6e9a11cd5755b93a3618.png$

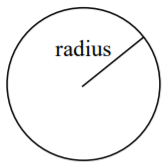
Círculo, radio$r$

Área:$\pi r^2$

Circunferencia:$ 2 \pi r $

$clipboard_e4356d8ca9ba07adcbbd71b698a023bce.png$

Definición: Volúmenes

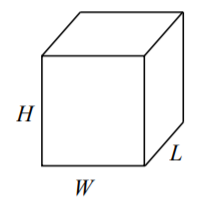
Caja Rectangular

Volumen:$L \cdot W \cdot H$

$clipboard_ed9c29b0190bf6b2391b9385514d7626a.png$

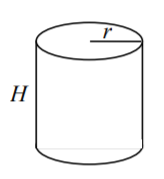
Cilindro

Volumen:$\pi r^2 H$

$clipboard_ec38ffaaca837b6df5351ac5105c1032b.png$

Ejemplo$\PageIndex{2}$

Si una pizza de 12 pulgadas de diámetro requiere 10 onzas de masa, ¿cuánta masa se necesita para una pizza de 16 pulgadas?

Solución

Para responder a esta pregunta, debemos considerar cómo escalará el peso de la masa. El peso se basará en el volumen de la masa. No obstante, dado que ambas pizzas tendrán aproximadamente el mismo grosor, el peso escalará con el área de la parte superior de la pizza. Podemos encontrar el área de cada pizza usando la fórmula para área de círculo,$A = \pi r^2$:

Una pizza de 12 pulgadas tiene un radio de 6 pulgadas, por lo que el área será de pulgadas$\pi \cdot 6^2 ≈ 113$ cuadradas.

Una pizza de 16 pulgadas tiene un radio de 8 pulgadas, por lo que el área será de pulgadas$\pi \cdot 8^2 ≈ 201$ cuadradas.

Observe que si ambas pizzas tuvieran 1 pulgada de grosor, los volúmenes serían 113 pulg$^3$ y 201 pulg$^3$ respectivamente, los cuales están en la misma proporción que las áreas. Como se mencionó anteriormente, dado que el grosor es el mismo para ambas pizzas, podemos ignorarlo con seguridad.

Ahora podemos establecer una proporción para encontrar el peso de la masa para una pizza de 16 pulgadas:

\[ \dfrac{10 \text{ ounces}}{113 \text{ in}^2} = \dfrac{x \text{ ounces}}{201 \text{ in}^2} \nonumber \]

Multiplica ambos lados por 201:$ x = 201 \cdot \dfrac{10}{113} ≈ 17.8 $ onzas de masa para una pizza de 16 pulgadas.

Es interesante señalar que si bien el diámetro es$ \dfrac{16}{12} = 1.33$ veces mayor, la masa requerida, que escala con área, es$1.33^2 = 1.78$ veces mayor.

Ejemplo$\PageIndex{3}$

Una empresa fabrica malvaviscos regulares y jumbo. El malvavisco regular tiene 25 calorías. ¿Cuántas calorías tendrá el malvavisco jumbo?

Solución

Esperaríamos que las calorías escalaran con el volumen. Dado que los malvaviscos tienen formas cilíndricas, podemos usar esa fórmula para encontrar el volumen. A partir de la cuadrícula en la imagen, podemos estimar el radio y la altura de cada malvavisco.

El malvavisco regular parece tener un diámetro de aproximadamente 3.5 unidades, dando un radio de 1.75 unidades, y una altura de aproximadamente 3.5 unidades. El volumen es sobre$ \pi (1.75)^2 (3.5) = 33.7 \text{ units}^3 $.

El malvavisco regular parece tener un diámetro de aproximadamente 5.5 unidades, dando un radio de 2.75 unidades, y una altura de aproximadamente 5 unidades. El volumen es sobre$ \pi (2.75)^2 (5) = 118.8 \text{ units}^3 $.

Ahora podríamos establecer una proporción, o tarifas de uso. El malvavisco regular tiene 25 calorías por 33.7 unidades cúbicas de volumen. El malvavisco jumbo tendrá:

\[ 118.8 \text{ units}^3 \cdot \dfrac{25 \text{ calories}}{33.7 \text{ units}^3 } = 88.1 \text{ calories} \nonumber \]

Es interesante señalar que si bien el diámetro y la altura son aproximadamente 1.5 veces mayores para el malvavisco jumbo, el volumen y las calorías son aproximadamente 1.53 = 3.375 veces mayores.

Pruébalo ahora 5

Un sitio web dice que necesitará 48 bolsas de arena de cincuenta libras para llenar una caja de arena que mida 8 pies por 8 pies por 1 pie. ¿Cuántas bolsas necesitarías para una caja de arena de 6 pies por 4 pies por 1 pie?

Ejemplo\(\PageIndex{1}\)

Solución

Definición: Áreas

Definición: Volúmenes

Ejemplo\(\PageIndex{2}\)

Solución

Ejemplo\(\PageIndex{3}\)

Solución

Pruébalo ahora 5