2.7: Ejercicios

Última actualización
Guardar como PDF

Page ID: 112917

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Habilidades

Tablero de conteo y Quipu

1. En la siguiente tabla de conteo peruana, determine cuántos de cada ítem está representado. Por favor, muestre todos sus cálculos junto con algún tipo de explicación de cómo obtuvo su respuesta. Anote la clave en la parte inferior del dibujo.

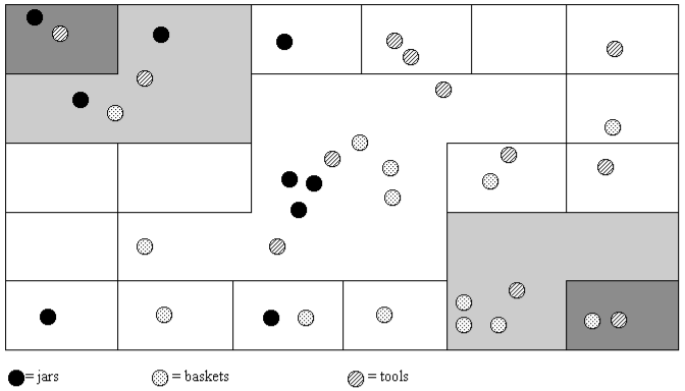
$clipboard_e52bad5879374b11e18cc8e695a22242c.png$

2. Dibuja un quipu con un cordón principal que tenga ramas (cordones H) que muestren cada uno de los siguientes números en ellos. (Debe producir un dibujo para este problema con el cable para la parte a a la izquierda y moviéndose hacia la derecha para las partes b a d.)

a.232 b. 5065

c.23,451 d. 3002

Conversiones básicas básicas

3. 423 en base 5 a base 10 4. 3044 en base 5 a base 10

5. 387 en base 10 a base 5 6. 2546 en base 10 a base 5

7. 110101 en base 2 a base 10 8. 11010001 en base 2 a base 10

9. 100 en base 10 a base 2 10. 2933 en base 10 a base 2

11. Convierta 653 en base 7 a base 10. 12. Convertir 653 en base 10 a base 7

13. 3412 en base 5 a base 2 14. 10011011 en base 2 a base 5

(Pista: convertir primero a la base 10 y luego a la base final deseada)

El Sistema Caidoz

Supongamos que iba a descubrir un antiguo sistema base−12 compuesto por doce símbolos. Llamemos a este sistema base el sistema Caidoz. Aquí están los símbolos para cada uno de los números del 0 al 11:

$clipboard_e1bcddf424fc8372414d881d81014d018.png$

Convierte cada uno de los siguientes números en Caidoz a base 10.

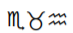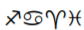
15. $clipboard_e00350f9ea64c6ba10fe9552dd60ebf1e.png$ 16. $clipboard_e03f960f5fc26ed022aa82c9d92f57a8c.png$

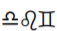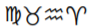
17. $clipboard_e68d8bddcb815705c4dda49f2c7661d31.png$ 18. $clipboard_e8018ff45249c861dbcad7448367ce7e5.png$

Convierte los siguientes números base 10 a Caidoz, usando los símbolos mostrados arriba.

19. 175 20. 3030

21. 10,000 22. 5507

Conversiones Mayas

Convierte los siguientes números a notación maya. Muestra tus cálculos utilizados para obtener tus respuestas.

23. 135 24. 234

25. 360 26. 1,215

27. 10,500 28. 1,100,000

Convierte los siguientes números mayas a números decimales (base-10). Mostrar todos los cálculos.

29. 30. 31. 32.

$clipboard_e3fb2339cf9f73369747d267eb58d94ca.png$ $clipboard_e9d2dc9a4f7d4b59692c734b202c0b2d3.png$ $clipboard_e07b6ec61139b4b27bfe82ebebf8022f6.png$ $clipboard_ed2882b94a7d14ddbca09828d8c8d0985.png$

James Bidwell ha sugerido que la adición maya se hizo “simplemente combinando barras y puntos y llevando al siguiente lugar más alto”. Continúa diciendo: “Después de la combinación de puntos y barras, el segundo paso es intercambiar cada cinco puntos por una barra en la misma posición”. Después de convertir los siguientes números base 10 en notación Maya vertical (en base 20, por supuesto), realice la suma indicada:

33. 32 + 11 34. 82 + 15

35. 35 + 148 36. 2412 + 5000

37. 450 + 844 38. 10,000 + 20,000

39. 4,500 + 3,500 40. 130,000 + 30,000

41. Usa el hecho de que los mayas tenían un sistema de números de base 20 para completar la siguiente tabla de multiplicación. Las entradas de la tabla deben estar en notación maya. Recuerda: Su cero se veía así... $clipboard_ee4b9a9151d1c9420f6786d6e9517ec23.png$ . Xerox y luego recorta la tabla de abajo, rellénala y pégala en tu tarea de tarea si no quieres duplicar la tabla con una regla. (Para pensar pero no escribir: Bidwell afirma que solo estas entradas son necesarias para la “multiplicación maya”. ¿Qué quiere decir?)

×	$clipboard_ecc0fcc19fba1f33e3ff6ff6ab92e9903.png$	$clipboard_e4a69f6f29d4ac994b89c7bbdc9e26b90.png$	$clipboard_e8f8c53e4595fd050c2d61f522607af23.png$	$clipboard_e7914728eae838fa4e156ffeea59d8150.png$	$clipboard_e8a1be9ad3cb7125139f928aac6549fe7.png$	$clipboard_ecc8c8b92e9a29650e52f6083d878ea1c.png$	$clipboard_e9f45277612525cc2def9477bb8660632.png$
$clipboard_e1b5fea820aedab3b112a0cafe858014d.png$
$clipboard_eed14c2045cdcff90295509e40cceb441.png$
$clipboard_e634fe22c8ba0523eb2dcbd660c32df62.png$
$clipboard_e7aa0de355ed821405bb0632a192bf053.png$
$clipboard_e49a7da137092424139836e1233056001.png$
$clipboard_edee3fd7bd094b810a1fd62cebda3c9e9.png$
$clipboard_ed05a163660a289c2cf704da4ab495a8b.png$

Conversiones binarias y hexadecimales

Las computadoras modernas operan en un mundo de interruptores electrónicos “on” y “off”, así que usa un sistema de conteo binario — base 2, que consta de solo dos dígitos: 0 y 1.

Convierta los siguientes números binarios a números decimales (base−10).

42. 1001 43. 1101

44. 110010 45. 101110

Convierta los siguientes números de base 10 a binario.

46. 7 47. 12

48. 36 49. 27

Cuatro dígitos binarios juntos pueden representar cualquier número de base 10 de 0 a 15. Para crear una representación más legible por humanos de números codificados binarios, comúnmente se usan números hexadecimales, base 16. En lugar de usar la notación 8,13,12 ₁₆ utilizada anteriormente, la letra A se usa para representar el dígito 10, B para 11, hasta F para 15, por lo que 8,13,12 ₁₆ se escribiría como 8DC.

Convierta los siguientes números hexadecimales a números decimales (base−10).

50. C3 51. 4D

52. 3A6 53. BC2

Convierta los siguientes números de base 10 a hexadecimales.

54. 152 55. 176

56. 2034 57. 8263

Sumar o restar en base 5 o en base 2.

58. 110 _cinco - 34 _cinco 59. 314 _cinco - 32 _cinco

60. 30 _cinco - 12 _cinco 61. 110 _dos + 10 _dos

62. 10011 _dos + 10000 _dos 63. 20 _cinco + 42 _cinco

64. 14 _cinco + 24 _cinco 65. 44 _cinco - 34 _cinco

Exploración

66. Cuáles son las ventajas y desventajas de bases distintas a las diez.

67. Supongamos que estás encargado de crear un sistema de números base 15. ¿Qué símbolos usarías para tu sistema y por qué? Explica con al menos dos ejemplos específicos cómo convertirías entre tu sistema base−15 y el sistema decimal.

68. Describir un aspecto interesante de la civilización maya que no discutimos en clase. Sus hallazgos deben provenir de alguna fuente, como un artículo de enciclopedia o un sitio de Internet y debe proporcionar referencias de los materiales que utilizó (ya sea la información de publicación o la dirección de Internet).

69. Para una tribu papúa en el sureste de Nueva Guinea, fue necesario traducir el pasaje bíblico Juan 5:5 “Y ahí estaba cierto hombre, que tenía una enfermedad de 30 y 8 años” a “Un hombre yacía enfermo a un hombre, ambas manos, cinco y tres años”. Con base en su propia comprensión de los sistemas de bases (y algún sentido común), proporcionar una explicación de la traducción. Por favor use oraciones completas para hacerlo. (Pista: Para hacer este problema, les pido que piensen en cómo funcionan los sistemas base, de dónde vienen y cómo se usan. No necesariamente encontrarás una “respuesta” en lecturas o tal... tendrás que pensarlo bien y llegar a una respuesta razonable. Solo asegúrate de explicar claramente por qué el pasaje se tradujo de la manera en que era).

70. El calendario maya se discutió ampliamente antes de diciembre de 2012. Investigue cómo funciona el calendario maya y cómo se relacionan los recuentos con el número basado en el uso.