4.4: Argumentos
- Page ID
- 112968
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Un argumento lógico es una afirmación de que un conjunto de premisas sustentan una conclusión. Existen dos tipos generales de argumentos: inductivos y deductivos.
Un argumento inductivo utiliza como premisas una colección de ejemplos específicos y los utiliza para proponer una conclusión general.
Un argumento deductivo utiliza como premisas una colección de declaraciones generales y las utiliza para proponer una situación específica como conclusión.
El argumento “cuando fui a la tienda la semana pasada olvidé mi bolso, y cuando fui hoy olvidé mi bolso. Siempre olvido mi bolso cuando voy a la tienda” es un argumento inductivo.
Solución
Los locales son:
- Olvidé mi bolso la semana pasada
- Hoy olvidé mi bolso
La conclusión es:
- Siempre olvido mi bolso
Observe que las premisas son situaciones específicas, mientras que la conclusión es una declaración general. En este caso, este es un argumento bastante débil, ya que se basa en sólo dos instancias.
El argumento “todos los días del año pasado, un avión sobrevuela mi casa a las 2 de la tarde Un avión sobrevolará mi casa todos los días a las 2 de la tarde” es un argumento inductivo más fuerte, ya que se basa en un conjunto de pruebas más amplio.
Un argumento inductivo nunca es capaz de probar la conclusión verdadera, pero puede proporcionar evidencia débil o fuerte para sugerir que puede ser cierta.
Muchas teorías científicas, como la teoría del big bang, nunca pueden probarse. En cambio, son argumentos inductivos apoyados por una amplia variedad de evidencias. Por lo general en la ciencia, una idea se considera una hipótesis hasta que ha sido bien probada, momento en el que se gradúa a ser considerada una teoría. Las teorías científicas comúnmente conocidas, como la teoría de la gravedad de Newton, han resistido años de pruebas y pruebas, aunque a veces necesitan ser ajustadas con base en nuevas pruebas. Para la gravedad, esto sucedió cuando Einstein propuso la teoría de la relatividad general.
Un argumento deductivo es más claramente válido o no, lo que los hace más fáciles de evaluar.
Un argumento deductivo se considera válido si todas las premisas son verdaderas, y la conclusión se desprende lógicamente de esas premisas. Es decir, las premisas son verdaderas, y la conclusión se desprende necesariamente de esas premisas.
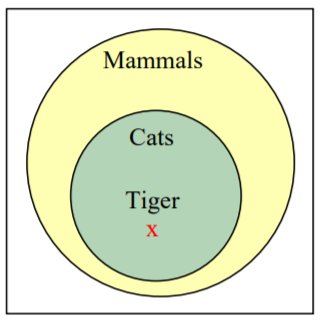
El argumento “Todos los gatos son mamíferos y un tigre es un gato, por lo que un tigre es un mamífero” es un argumento deductivo válido.
Los locales son:
- Todos los gatos son mamíferos
- Un tigre es un gato
La conclusión es:
- Un tigre es un mamífero
Ambas premisas son verdaderas. Para ver que las premisas deben llevar lógicamente a la conclusión, un enfoque sería utilizar un diagrama de Venn. Desde la primera premisa, podemos concluir que el conjunto de gatos es un subconjunto del conjunto de mamíferos. Desde la segunda premisa, se nos dice que un tigre yace dentro del conjunto de gatos. A partir de eso, podemos ver en el diagrama de Venn que el tigre también se encuentra dentro del conjunto de mamíferos, por lo que la conclusión es válida.
Para analizar un argumento con un diagrama de Venn
- Dibuja un diagrama de Venn basado en las premisas del argumento
- Si los locales son insuficientes para determinar qué determina la ubicación de un elemento, indíquelo.
- El argumento es válido si queda claro que la conclusión debe ser verdadera
Premisa: Todos los bomberos conocen RCP
Premisa: Jill conoce la RCP
Conclusión: Jill es bombero
Solución
Desde la primera premisa, sabemos que todos los bomberos se encuentran dentro del conjunto de quienes conocen la RCP. Desde la segunda premisa, sabemos que Jill es miembro de ese conjunto más grande, pero no tenemos suficiente información para saber si ella también es miembro del subconjunto más pequeño que son los bomberos.
Dado que la conclusión no necesariamente se desprende de las premisas, este es un argumento inválido, independientemente de que Jill en realidad sea bombero.
Es importante señalar que si Jill es o no en realidad bombero no es importante para evaluar la validez del argumento; sólo nos preocupa si las premisas son suficientes para probar la conclusión.
Determinar la validez de este argumento:
Premisa: No hay vacas moradas
Premisa: Fido no es una vaca
Conclusión: Fido es morado
Además de estas premisas de estilo categórico de la forma “todos ___”, “algunos ____”, y “no ____”, también es común ver premisas que son implicaciones.
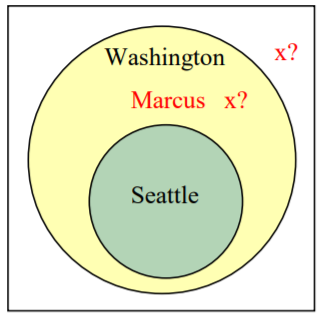Premisa: Si vives en Seattle, vives en Washington.
Premisa: Marcus no vive en Seattle
Conclusión: Marcus no vive en Washington
Solución
Desde la primera premisa, sabemos que el conjunto de personas que viven en Seattle está dentro del conjunto de quienes viven en Washington. Desde la segunda premisa, sabemos que Marcus no miente en el set de Seattle, pero no tenemos suficiente información para saber si Marcus vive o no en Washington o no. Este es un argumento inválido.
Considera el argumento “Eres un hombre casado, entonces debes tener esposa”.
Solución
Este es un argumento inválido, ya que hay, al menos en partes del mundo, hombres que están casados con otros hombres, por lo que la premisa no es insuficiente para implicar la conclusión.
Algunos argumentos se analizan mejor usando tablas de verdad.
Considerar el argumento
Premisa: Si compraste pan, entonces fuiste a la tienda
Premisa: Compraste pan
Conclusión: Fuiste a la tienda
Si bien este ejemplo es ojalá sea bastante obviamente un argumento válido, podemos analizarlo usando una tabla de verdad representando simbólicamente cada una de las premisas. Entonces podemos mirar la implicación de que las premisas juntas implican la conclusión. Si la tabla de verdad es una tautología (siempre verdadera), entonces el argumento es válido.
Conseguiremos\(B\) representar “compraste pan” y\(S\) representaremos “fuiste a la tienda”. Entonces el argumento se convierte en:
Premisa:\(B → S\)
Premisa:\(B\)
Conclusión:\(S\)
Para probar la validez, miramos si la combinación de ambas premisas implica la conclusión; ¿es cierto que\(\left[ (B→S) ⋀ B \right] → S\)?
| B | S | B→S | (B→S) B | [(B→S) B] → S | |||
| T | T | T | T | T | |||
| T | F | F | F | T | |||
| F | T | T | F | T | |||
| F | F | T | F | T | |||
Dado que la tabla de la verdad para siempre\(\left[ (B→S) ⋀ B \right] → S\) es verdadera, este es un argumento válido.
Determina si el argumento es válido:
Premisa: Si tengo una pala puedo cavar un hoyo.
Premisa: cavé un hoyo
Conclusión: Por lo tanto, tenía una pala
Para analizar un argumento con una tabla de verdad:
- Representar simbólicamente cada una de las premisas
- Crear una declaración condicional, uniendo todas las premisas con y para formar el antecedente, y utilizando la conclusión como consecuente.
- Crear una tabla de verdad para esa declaración. Si siempre es cierto, entonces el argumento es válido.
Premisa: Si voy al centro comercial, entonces compraré jeans nuevos
Premisa: Si compro jeans nuevos, compraré una camisa para acompañarlo
Conclusión: Si llego al centro comercial, compraré una playera.
Solución
Let\(M\) = voy al centro comercial,\(J\) = compro jeans, y\(S\) = compro una playera.
Las premisas y conclusión pueden ser declaradas como:
Premisa: M → J
Premisa: J → S
Conclusión: M → S
Podemos construir una tabla de verdad para\([(M→J) ⋀ (J→S)] → (M→S)\)
| M | J | S | M→J | J→S | (M→J) (J→S) | M→S | [(M→J) (J→S)] → (M→S) | |||
| T | T | T | T | T | T | T | T | |||
| T | T | F | T | F | F | F | T | |||
| T | F | T | F | T | F | T | T | |||
| T | F | F | F | T | F | F | T | |||
| F | T | T | T | T | T | T | T | |||
| F | T | F | T | F | F | T | T | |||
| F | F | T | T | T | T | T | T | |||
| F | F | F | T | T | T | T | T | |||
De la tabla de la verdad, podemos ver que este es un argumento válido.
El problema anterior es un ejemplo de silogismo.
Un silogismo es una implicación derivada de otras dos, donde la consecuencia de uno es el antecedente a la otra. La forma general de un silogismo es:
Premisa: p → q
Premisa: q → r
Conclusión: p → r
Esto a veces se llama la propiedad transitiva para su implicación.
Premisa: Si trabajo duro, conseguiré un aumento.
Premisa: Si consigo un aumento, compraré un bote.
Conclusión: Si no compro un barco, no debo haber trabajado duro.
Solución
Si dejamos que W = trabajar duro, R = conseguir un aumento, y B = comprar un barco, entonces podemos representar nuestro argumento simbólicamente:
Premisa: H → R
Premisa: R → B
Conclusión: ~ B → ~ H
Podríamos construir una tabla de verdad para este argumento, pero en su lugar, usaremos la notación del contrapositivo que aprendimos antes para señalar que la implicación ~ B → ~ H es equivalente a la implicación H → B. Reescrito, podemos ver que esta conclusión es efectivamente un silogismo lógico derivado de las premisas.
¿Es válido este argumento?
Premisa: Si voy a la fiesta, mañana estaré muy cansada.
Premisa: Si voy a la fiesta, podré ver amigos.
Conclusión: Si no veo amigos, mañana no me cansaré.
Lewis Carroll, autor de Alicia en el país de las maravillas, fue profesor de matemáticas y lógica, y escribió dos libros sobre lógica. En ellas, propondría premisas como rompecabezas, para ser conectadas mediante silogismos.
Resuelve el rompecabezas. Es decir, encontrar una conclusión lógica a partir de estas premisas.
- Todos los bebés son ilógicos.
- No se desprecia a nadie que pueda manejar a un cocodrilo.
- Personas ilógicas son despreciadas
Solución
Que B = es un bebé, D = es despreciado, I = es ilógico, y M = puede manejar un cocodrilo.
Entonces podemos escribir las premisas como:
B → I
M → ~D
I → D
Desde la primera y tercera premisas, podemos concluir que B → D; que los bebés son despreciados. Usando el contrapositivo del segundo premisado, D → ~M, podemos concluir que B → ~M; que los bebés no pueden manejar cocodrilos.
Si bien tonta, esta es una conclusión lógica desde las premisas dadas.