4.9: Resolver ecuaciones con fracciones
- Page ID
- 113451
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Deshacer la resta
Todavía podemos agregar la misma cantidad a ambos lados de una ecuación sin cambiar la solución.
Ejemplo 1
Resolver para x:\(x - \frac{5}{6} = \frac{1}{3}\).
Solución
Para “deshacer” restando 5/6, agregue 5/6 a ambos lados de la ecuación y simplifique.
\[ \begin{aligned} x - \frac{5}{6} = \frac{1}{3} ~ & \textcolor{red}{ \text{ Original equation.}} \\ x - \frac{5}{6} + \frac{5}{6} = \frac{1}{3} + \frac{5}{6} ~ & \textcolor{red}{ \text{ Add } \frac{5}{6} \text{ to both sides.}} \\ x = \frac{1 \cdot 2}{3 \cdot 2} + \frac{5}{6} ~ & \textcolor{red}{ \text{ Equivalent fractions, LCD = 6.}} \\ x = \frac{2}{6} + \frac{5}{6} ~ & \textcolor{red}{ \text{ Simplify.}} \\ x = \frac{7}{6} ~ & \textcolor{red}{ \text{ Add.}} \end{aligned}\nonumber \]
Es perfectamente aceptable dejar tu respuesta como una fracción impropia. Si lo deseas, o si te indican hacerlo, puedes cambiar tu respuesta a una fracción mixta (7 dividido por 6 es 1 con un resto de 1). Eso es\(x = 1 \frac{1}{6}\).
Comprobación de la solución
Sustituye 7/6 por x en la ecuación original y simplifica.
\[ \begin{aligned} x - \frac{5}{6} = \frac{1}{3} ~ & \textcolor{red}{ \text{ Original equation.}} \\ \frac{7}{6} - \frac{5}{6} = \frac{1}{3} ~ & \textcolor{red}{ \text{ Substitute 7/6 for } x.} \\ \frac{2}{6} = \frac{1}{3} ~ & \textcolor{red}{ \text{ Subtract.}} \\ \frac{1}{3} = \frac{1}{3} ~ & \textcolor{red}{ \text{ Reduce.}} \end{aligned}\nonumber \]
Debido a que la última afirmación es cierta, concluimos que 7/6 es una solución de la ecuación x − 5/6 = 1/3.
Adición de deshacer
Aún se puede restar la misma cantidad de ambos lados de una ecuación sin cambiar la solución.
Ejemplo 2
Resolver para x:\(x + \frac{2}{3} = - \frac{3}{5}\).
Solución
Para “deshacer” sumando 2/3, restar 2/3 de ambos lados de la ecuación y simplificar.
\[ \begin{aligned} x + \frac{2}{3} = - \frac{3}{5} ~ & \textcolor{red}{ \text{ Original equation.}} \\ x + \frac{2}{3} - \frac{2}{3} = - \frac{3}{5} - \frac{2}{3} ~ & \textcolor{red}{ \text{ Subtract } \frac{2}{3} \text{ from both sides.}} \\ x = - \frac{3 \cdot 3}{5 \cdot 3} - \frac{2 \cdot 5}{3 \cdot 5} ~ & \textcolor{red}{ \text{ Equivalent fractions, LCD = 15.}} \\ x = - \frac{9}{15} - \frac{10}{15} ~ & \textcolor{red}{ \text{ Simplify.}} \\ x = - \frac{19}{15} ~ & \textcolor{red}{ \text{ Subtract.}} \end{aligned}\nonumber \]
Se anima a los lectores a verificar esta solución en la ecuación original.
Ejercicio
Resolver para x:\(x + \frac{3}{4} = - \frac{1}{2}\)
- Responder
-
−5/4
Deshacer multiplicación
Nosotros “deshacemos” la multiplicación dividiendo. Por ejemplo, para resolver la ecuación 2 x = 6, dividiríamos ambos lados de la ecuación por 2. De manera similar, podríamos dividir ambos lados de la ecuación
\[ \frac{3}{5} x = \frac{4}{10}\nonumber \]
por 3/5. No obstante, es más eficiente aprovechar los recíprocos. Para mayor comodidad, recordamos a los lectores la Propiedad Multiplicativa Inversa.
Propiedad inversa multiplicativa
Que a/b sea cualquier fracción. El número b/a se llama el inverso multiplicativo o recíproco de a/b. El producto de los recíprocos es 1.
\[ \frac{a}{b} \cdot \frac{b}{a} = 1.\nonumber \]
Pongamos a trabajar nuestro conocimiento de los recíprocos.
Ejemplo 3
Resolver para x:\(\frac{3}{5}x = \frac{4}{10}\).
Solución
Para “deshacer” multiplicando por 3/5, multiplicar ambos lados por el recíproco 5/3 y simplificar.
\[ \begin{aligned} \frac{3}{5} x = \frac{4}{10} ~ & \textcolor{red}{ \text{ Original equation.}} \\ \frac{5}{3} \left( \frac{3}{5} x \right) = \frac{5}{3} \left( \frac{4}{10} \right) & ~ \textcolor{red}{ \text{ Multiply both sides by 5/3.}} \\ \left( \frac{5}{3} \cdot \frac{3}{5} \right) x = \frac{20}{30} ~ & \textcolor{red}{ \begin{array}{l} \text{ On the left, use the associative property to regroup.} \\ \text{ On the right, multiply.} \end{array}} \\ 1x = \frac{2}{3} ~ & \textcolor{red}{ \begin{array}{l} \text{ On the left, } \frac{5}{3} \cdot \frac{3}{5} = 1. \\ \text{ On the right, reduce: } \frac{20}{30} = \frac{2}{3}. \end{array}} \\ x = \frac{2}{3} ~ & \textcolor{red}{ \text{ On the left, } 1x = x.} \end{aligned}\nonumber \]
Comprobación de la solución
Sustituye 2/3 por x en la ecuación original y simplifica.
\[ \begin{aligned} \frac{3}{5} x = \frac{4}{10} ~ & \textcolor{red}{ \text{ Original equation.}} \\ \frac{3}{5} \left( \frac{2}{3} \right) = \frac{4}{10} ~ & \textcolor{red}{ \text{ Substitute 2/3 for }x.} \\ \frac{6}{15} = \frac{4}{10} ~ & \textcolor{red}{ \text{ Multiply numerators; multiply denominators.}} \\ \frac{2}{5} = \frac{2}{5} ~ & \textcolor{red}{ \text{ Reduce both sides to lowest terms.}} \end{aligned}\nonumber \]
Debido a que esta última afirmación es cierta, concluimos que 2/3 es una solución de la ecuación (3/5) x = 4/10.
Ejercicio
Resolver para y:\( \frac{2}{3} y = \frac{4}{5}\)
- Responder
-
6/5
Ejemplo 4
Resolver para x:\(- \frac{8}{9} x = \frac{5}{18}\).
Solución
Para “deshacer” multiplicando por −8/9, multiplique ambos lados por el recíproco −9/8 y simplifique.
\[ \begin{aligned} - \frac{8}{9} x = \frac{5}{18} ~ & \textcolor{red}{ \text{ Original equation.}} \\ - \frac{9}{8} \left( - \frac{8}{9} x \right) = - \frac{9}{8} \left( \frac{5}{18} \right) ~ & \textcolor{red}{ \text{ Multiply both sides by } -9/8.} \\ \left[ - \frac{9}{8} \cdot \left( - \frac{8}{9} \right) \right] x = - \frac{3 \cdot 3}{2 \cdot 2 \cdot 2} \cdot \frac{5}{2 \cdot 3 \cdot 3} ~ & \textcolor{red}{ \begin{array}{l} \text{ On the left, use the associative property to regroup.} \\ \text{ On the right, prime factor.} \end{array}} 1x = \frac{ \cancel{3} \cdot \cancel{3}}{2 \cdot 2 \cdot 2} \cdot \frac{5}{2 \cdot \cancel{3} \cdot \cancel{3}} ~ & \textcolor{red}{ \begin{array}{l} \text{ On the left, } - \frac{9}{8} \cdot \left( - \frac{8}{9} \right) = 1. \\ \text{ On the right, cancel common factors.} \end{array}} \\ x = - \frac{5}{16} ~ & \textcolor{red}{ \text{ On the left, } 1x = x. \text{ Multiply on the right.}} \end{aligned}\nonumber \]
Se anima a los lectores a verificar esta solución en la ecuación original.
Ejercicio
Resolver para z:\(− \frac{2}{7} z = \frac{4}{21}\)
- Responder
-
−2/3
Borrar Fracciones de la Ecuación
Si bien la técnica demostrada en los ejemplos anteriores es una técnica matemática sólida, trabajar con fracciones en una ecuación no siempre es el uso más eficiente de tu tiempo.
Borrar fracciones de la ecuación
Para borrar todas las fracciones de una ecuación, multiplique ambos lados de la ecuación por el mínimo denominador común de las fracciones que aparecen en la ecuación.
Pongamos a trabajar esta idea.
Ejemplo 5
En el Ejemplo 1, se nos pidió resolver la siguiente ecuación para x:
\[x - \frac{5}{6} = \frac{1}{3}.\nonumber \]
Tómese un momento para revisar la técnica de solución en el Ejemplo 1. Ahora resolveremos esta ecuación limpiando primero todas las fracciones de la ecuación.
Solución
Multiplique ambos lados de la ecuación por el mínimo denominador común para las fracciones que aparecen en la ecuación.
\[ \begin{aligned} x - \frac{5}{6}= \frac{1}{3} ~ & \textcolor{red}{ \text{ Original equation.}} \\ 6 \left( x - \frac{5}{6} \right) = 6 \left( \frac{1}{3} \right) ~ & \textcolor{red}{ \text{ Multiply both sides by 6.}} \\ 6x - 6 \left( \frac{5}{6} \right) = 6 \left( \frac{1}{3} \right) ~ & \textcolor{red}{ \text{ Distribute the 6.}} \\ 6x-5 = 2 ~ & \textcolor{red}{ \text{ On each side, multiply first.}} \\ ~ & \textcolor{red}{6 \left( \frac{5}{6} \right) = 5 \text{ and } 6 \left( \frac{1}{3} \right) = 2.} \end{aligned}\nonumber \]
Tenga en cuenta que la ecuación ahora está completamente clara de fracciones, lo que la convierte en una ecuación mucho más simple de resolver.
\[ \begin{aligned} 6x - 5 + 5 = 2 + 5 ~ & \textcolor{red}{ \text{ Add 5 to both sides.}} \\ 6x = 7 ~ & \textcolor{red}{ \text{ Simplify both sides.}} \\ \frac{6x}{6} = \frac{7}{6} ~ & \textcolor{red}{ \text{ Divide both sides by 6.}} \\ x = \frac{7}{6} ~ & \textcolor{red}{ \text{ Simplify.}} \end{aligned}\nonumber \]
Tenga en cuenta que esta es la misma solución que se encuentra en el Ejemplo 1.
Ejercicio
Resolver para t:\(t - \frac{2}{7} = - \frac{1}{4}\)
- Responder
-
1/28
Ejemplo 6
En el Ejemplo 4, se nos pidió resolver la siguiente ecuación para x.
\[- \frac{8}{9}x = \frac{5}{18}\nonumber \]
Tómese un momento para revisar la solución en el Ejemplo 4. Ahora resolveremos esta ecuación limpiando primero todas las fracciones de la ecuación.
Solución
Multiplique ambos lados de la ecuación por el mínimo denominador común para las fracciones que aparecen en la ecuación.
\[ \begin{aligned} - \frac{8}{9} x = \frac{5}{18} ~ & \textcolor{red}{ \text{ Original equation.}} \\ 18 \left( - \frac{8}{9} x \right) = 18 \left( \frac{5}{18} \right) ~ & \textcolor{red}{ \text{ Multiply both sides by 18.}} \\ -16x=5 ~ & \textcolor{red}{ \text{ On each side, cancel and multiply.}} \\ ~ & \textcolor{red}{ 18 \left( - \frac{8}{9} \right) = -16 \text{ and } 18 \left( \frac{5}{18} \right) = 5.} \end{aligned}\nonumber \]
Tenga en cuenta que la ecuación ahora está completamente libre de fracciones. Continuando,
\[ \begin{aligned} \frac{-16x}{-16} = \frac{5}{-16} ~ & \textcolor{red}{ \text{ Divide both sides by } -16.} \\ x = - \frac{5}{16} ~ & \textcolor{red}{ \text{ Simplify.}} \end{aligned}\nonumber \]
Tenga en cuenta que esta es la misma que la solución que se encuentra en el Ejemplo 4.
Ejercicio
Resolver para u:
\[ - \frac{7}{9} u = \frac{14}{27}\nonumber \]
- Responder
-
−2/3
Ejemplo 7
Resolver para x:\(\frac{2}{3}x + \frac{3}{4} = \frac{1}{2}\).
Solución
Multiplique ambos lados de la ecuación por el mínimo denominador común para las fracciones que aparecen en la ecuación.
\[ \begin{aligned} \frac{2}{3} x + \frac{3}{4} = \frac{1}{2} ~ & \textcolor{red}{ \text{ Original equation.}} \\ 12 \left( \frac{2}{3} x + \frac{3}{4} = \right) = 12 \left( \frac{1}{2} \right) ~ & \textcolor{red}{ \text{ Multiply both sides by 12.}} \\ 12 \left( \frac{2}{3}x \right) + 12 \left( \frac{3}{4} \right) = 12 \left( \frac{1}{2} \right) ~ & \textcolor{red}{ \text{ On the left, distribute 12.}} \\ 8x + 9 = 6 ~ & \textcolor{red}{ \text{ Multiply: } 12 \left( \frac{2}{3} x \right) = 8x, ~ 12 \left( \frac{3}{4} \right) = 9,} \\ ~ & \textcolor{red}{ \text{ and } 12 \left( \frac{1}{2} \right) = 6.} \end{aligned}\nonumber \]
Tenga en cuenta que la ecuación ahora está completamente libre de fracciones. Necesitamos aislar los términos que contienen x en un lado de la ecuación.
\[ \begin{aligned} 8x + 9 - 9 = 6 - 9 ~ & \textcolor{red}{ \text{ Subtract 9 from both sides.}} \\ 8x = - 3 ~ & \textcolor{red}{ \text{ Simplify both sides.}} \\ \frac{8x}{8} = \frac{-3}{8} ~ & \textcolor{red}{ \text{ Divide both sides by 8.}} \\ x = - \frac{3}{8} ~ & \textcolor{red}{ \text{ Simplify both sides.}} \end{aligned}\nonumber \]
Se anima a los lectores a verificar esta solución en la ecuación original.
Ejercicio
Resolver para r:\(\frac{3}{4} r + \frac{2}{3} = \frac{1}{2}\)
- Responder
-
−2/9
Ejemplo 8
Resolver para x:\( \frac{2}{3} - \frac{3x}{4} = \frac{x}{2} - \frac{1}{8}.\)
Solución
Multiplique ambos lados de la ecuación por el mínimo denominador común para las fracciones de la ecuación.
\[ \begin{aligned} \frac{2}{3} - \frac{3x}{4} = \frac{x}{2} - \frac{1}{8} ~ & \textcolor{red}{ \text{ Original equation.}} \\ 24 \left( \frac{2}{3} - \frac{3x}{4} \right) = 24 \left( \frac{x}{2} - \frac{1}{8} \right) ~ & \textcolor{red}{ \text{ Multiply both sides by 24.}} \\ 24 \left( \frac{2}{3} \right) - 24 \left( \frac{3x}{4} \right) = 24 \left( \frac{x}{2} \right) - 24 \left( \frac{1}{8} \right) ~ & \textcolor{red}{ \text{ On both sides, distribute 24.}} \\ 16 - 18x = 12x - 3 ~ & \textcolor{red}{ \text{ Left: } 24 \left( \frac{2}{3} \right) = 16, ~ 24 \left( \frac{3x}{4} \right) = 18x.} \\ ~ & \textcolor{red}{ \text{ Right: } 24 \left( \frac{x}{2} \right) = 12x, ~ 24 \left( \frac{1}{8} \right) = 3.} \end{aligned}\nonumber \]
Tenga en cuenta que la ecuación ahora está completamente libre de fracciones. Necesitamos aislar los términos que contienen x en un lado de la ecuación.
\[ \begin{aligned} 16 - 18x - 12x = 12x - 3 - 12x ~ & \textcolor{red}{ \text{ Subtract } 12x \text{ from both sides.}} \\ 16 - 30x = -3 ~ & \textcolor{red}{ \begin{aligned} \text{ Left: } -18x - 12x = -30x. \\ \text{ Right: } 12x - 12x = 0. \end{aligned}} \\ 16 - 30x - 16 = -3 - 16 ~ & \textcolor{red}{ \text{ Subtract 16 from both sides.}} \\ -30x = -19 ~ & \textcolor{red}{ \begin{aligned} \text{ Left: } 16-16=0. \\ \text{ Right: } -3 - 16 = -19. \end{aligned}} \\ \frac{-30x}{-30} = \frac{-19}{-30} ~ & \textcolor{red}{ \text{ Divide both sides by } -30.} \\ x = \frac{19}{30} ~ & \textcolor{red}{ \text{ Simplify both sides.}} \end{aligned}\nonumber \]
Se anima a los lectores a verificar esta solución en la ecuación original.
Ejercicio
Resolver para s:\( \frac{3}{2} - \frac{2s}{5} = \frac{s}{3} - \frac{1}{5}\).
- Responder
-
Agrega textos aquí. No elimine primero este texto.
Aplicaciones
Veamos algunas aplicaciones que involucran ecuaciones que contienen fracciones. Para mayor comodidad, repetimos los Requisitos para Soluciones de Problemas de Word.
Requisitos para soluciones de problemas de Word
- Configura un Diccionario de Variables. Debes dejar saber a tus lectores qué representa cada variable en tu problema. Esto se puede lograr de varias maneras:
- Declaraciones como “Que P represente el perímetro del rectángulo”.
- Etiquetar valores desconocidos con variables en una tabla.
- Etiquetar cantidades desconocidas en un boceto o diagrama.
- Configura una Ecuación. Toda solución a un problema verbal debe incluir una ecuación cuidadosamente elaborada que describa con precisión las restricciones en la declaración del problema.
- Resuelve la Ecuación. Siempre debes resolver la ecuación establecida en el paso anterior.
- Responda a la Pregunta. Este paso se pasa por alto fácilmente. Por ejemplo, el problema podría preguntar por la edad de Jane, pero la solución de tu ecuación da la edad de la hermana de Jane, Liz. Asegúrate de responder la pregunta original hecha en el problema. Su solución debe escribirse en una oración con las unidades correspondientes. 5. Mira hacia atrás. Es importante señalar que este paso no implica que simplemente deba verificar su solución en su ecuación. Después de todo, es posible que tu ecuación modele incorrectamente la situación del problema, por lo que podrías tener una solución válida a una ecuación incorrecta. La pregunta importante es: “¿Tiene sentido tu respuesta con base en las palabras de la declaración original del problema”.
Ejemplo 9
En el tercer cuarto de un juego de basquetbol, los locutores informaron a la multitud que la asistencia al juego fue de 12,250. Si esto es dos tercios de la capacidad, encuentra la capacidad total de asientos para la arena de básquetbol.
Solución
Seguimos los Requisitos para Soluciones de Problemas de Word.
1. Configura un Diccionario de Variables. Deje que F represente la capacidad total de asientos. Nota: Es mucho mejor usar una variable que “suene como” la cantidad que representa. En este caso, dejar que F represente la capacidad total de asientos es mucho más descriptivo que usar x para representar la capacidad total de asientos.
2. Configura una Ecuación. Dos tercios de la capacidad total de asientos es de 12,250.
\[ \begin{aligned} \colorbox{cyan}{Two-thirds} & \text{ of } & \colorbox{cyan}{Full Seating Capacity} & \text{ is } & 12,250 \\ \frac{2}{3} & \cdot & F & = & 12,250 \end{aligned}\nonumber \]
Por lo tanto, la ecuación es
\[ \frac{2}{3} F = 12250.\nonumber \]
3. Resuelve la Ecuación. Multiplica ambos lados por 3 para despejar fracciones, luego resuelve.
\[ \begin{aligned} \frac{2}{3} F = 12250 ~ & \textcolor{red}{ \text{ Original equation.}} \\ 3 \left( \frac{2}{3} F \right) = 3(12250) ~ & \textcolor{red}{ \text{ Multiply both sides by 3.}} \\ 2F = 36750 ~ & \textcolor{red}{ \text{ Simplify both sides.}} \\ \frac{2F}{2} = \frac{36750}{2} ~ & \textcolor{red}{ \text{ Divide both sides by 2.}} \\ F = 18375 ~ & \textcolor{red}{ \text{ Simplify both sides.}} \end{aligned}\nonumber \]
4. Responda a la Pregunta. La capacidad total de asientos es de 18,375.
5. Mira hacia atrás. Las palabras del problema indican que 2/3 de la capacidad de asientos es de 12,250. Tomemos dos tercios de nuestra respuesta y veamos qué obtenemos.
\[ \begin{aligned} \frac{2}{3} \cdot 18375 & = \frac{2}{3} \cdot \frac{18375}{1} \\ & = \frac{2}{3} \cdot \frac{3 \cdot 6125}{1} \\ & = \frac{2}{ \cancel{3}} \cdot \frac{ \cancel{3} \cdot 6125}{1} \\ & = 12250 \end{aligned}\nonumber \]
Esta es la asistencia correcta, por lo que nuestra solución es correcta.
Ejercicio
La asistencia para el juego de los Celtics fue de 9,510. Si esto es 3/4 de capacidad, ¿cuál es la capacidad de la arena de los celtas?
- Responder
-
12,680
Ejemplo 10
El área de un triángulo es de 20 pulgadas cuadradas. Si la longitud de la base es\(2 \frac{1}{2}\) pulgadas, encuentra la altura (altitud) del triángulo.
Solución
Seguimos los Requisitos para Soluciones de Problemas de Word.
1. Configura un Diccionario de Variables. Nuestro diccionario de variables tomará la forma de un diagrama bien etiquetado.
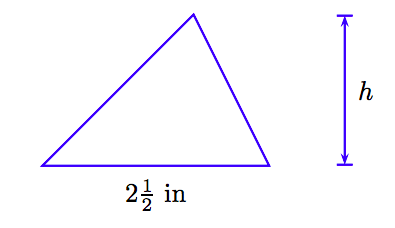
2. Configura una Ecuación. El área A de un triángulo con base b y altura h es
\[A = \frac{1}{2} bh.\nonumber \]
Sustituto A = 20 y b =\(2 \frac{1}{2}\).
\[20 = \frac{1}{2} \left( 2 \frac{1}{2} \right) h.\nonumber \]
3. Resuelve la Ecuación. Cambie la fracción mixta a una fracción impropia, luego simplifique.
\[ \begin{aligned} 20 = \frac{1}{2} \left( 2 \frac{1}{2} \right) h ~ & \textcolor{red}{ \text{ Original equation.}} \\ 20 = \frac{1}{2} \left( \frac{5}{2} \right) h ~ & \textcolor{red}{ \text{ Mixed to improper: } 2 \frac{1}{2} = \frac{5}{2}.} \\ 20 = \left( \frac{1}{2} \cdot \frac{5}{2} \right) h ~ & \textcolor{red}{ \text{ Associative property.}} \\ 20 = \frac{5}{4} h ~ & \textcolor{red}{ \text{ Multiply: } \frac{1}{2} \cdot \frac{5}{2} = \frac{5}{4}.} \end{aligned}\nonumber \]
Ahora, multiplica ambos lados por 4/5 y resuelve.
\[ \begin{aligned} \frac{4}{5} (20) = \frac{4}{5} \left( \frac{5}{4} h \right) ~ & \textcolor{red}{ \text{ Multiply both sides by 4/5.}} \\ 16 = h ~ & \textcolor{red}{ \text{ Simplify: } \frac{4}{5} (20) = 16} \\ ~ & \textcolor{red}{ \text{ and } \frac{4}{5} \cdot \frac{5}{4} = 1.} \end{aligned}\nonumber \]
4. Responda a la Pregunta. La altura del triángulo es de 16 pulgadas.
5. Mira hacia atrás. Si la altura es de 16 pulgadas y la base es\(2 \frac{1}{2}\) pulgadas, entonces el área es
\[ \begin{aligned} A & = \frac{1}{2} \left( 2 \frac{1}{2} \right) (16) \\ & = \frac{1}{2} \cdot \frac{5}{2} \cdot \frac{16}{1} \\ & = \frac{5 \cdot 16}{2 \cdot 2} \\ & = \frac{(5) \cdot (2 \cdot 2 \cdot 2 \cdot 2)}{(2) \cdot (2)} \\ & = \frac{5 \cdot \cancel{2} \cdot \cancel{2} \cdot 2 \cot 2}{ \cancel{2} \cdot \cancel{2}} & = 20 \end{aligned}\nonumber \]
Esta es el área correcta (20 pulgadas cuadradas), por lo que nuestra solución es correcta.
Ejercicio
El área de un triángulo es de 161 pies cuadrados. Si la base del triángulo mide\(40 \frac{1}{4}\) pies, encuentra la altura del triángulo.
- Responder
-
8 pies
Ejercicios
1. ¿1/4 es una solución de la ecuación\(x + \frac{5}{8} = \frac{5}{8}\)?
2. ¿1/4 es una solución de la ecuación\(x + \frac{1}{3} = \frac{5}{12}\)?
3. ¿Es −8/15 una solución de la ecuación\(\frac{1}{4} x = − \frac{1}{15}\)?
4. ¿Es −18/7 una solución de la ecuación\(− \frac{3}{8} x = \frac{25}{28}\)?
5. ¿1/2 es una solución de la ecuación\(x + \frac{4}{9} = \frac{17}{18}\)?
6. ¿1/3 es una solución de la ecuación\(x + \frac{3}{4} = \frac{13}{12}\)?
7. ¿3/8 es una solución de la ecuación\(x − \frac{5}{9} = − \frac{13}{72}\)?
8. ¿1/2 es una solución de la ecuación\(x − \frac{3}{5} = − \frac{1}{10}\)?
9. ¿Es 2/7 una solución de la ecuación\(x − \frac{4}{9} = − \frac{8}{63}\)?
10. ¿El 1/9 es una solución de la ecuación\(x − \frac{4}{7} = − \frac{31}{63}\)?
11. ¿El 8/5 es una solución de la ecuación\( \frac{11}{14}x = \frac{44}{35}\)?
12. ¿Es 16/9 una solución de la ecuación\(\frac{13}{18} x = \frac{104}{81}\)?
En Ejercicios 13-24, resuelve la ecuación y simplifica tu respuesta.
13. \(2x − 3=6x + 7\)
14. \(9x − 8 = −9x − 3\)
15. \(−7x +4=3x\)
16. \(6x +9= −6x\)
17. \(−2x = 9x − 4\)
18. \(−6x = −9x + 8\)
19. \(−8x = 7x − 7\)
20. \(−6x = 5x + 4\)
21. \(−7x +8=2x\)
22. \(−x − 7=3x\)
23. \(−9x +4=4x − 6\)
24. \(−2x +4= x − 7\)
En Ejercicios 25-48, resuelve la ecuación y simplifica tu respuesta.
25. \(x + \frac{3}{2 = \frac{1}{2}\)
26. \(x − \frac{3}{4} = \frac{1}{4}\)
27. \(− \frac{9}{5} x = \frac{1}{2}\)
28. \(\frac{7}{3} x = − \frac{7}{2}\)
29. \(\frac{3}{8} x = \frac{8}{7}\)
30. \(− \frac{1}{9} x = − \frac{3}{5}\)
31. \(\frac{2}{5} x = − \frac{1}{6}\)
32. \(\frac{1}{6} x = \frac{2}{9}\)
33. \(− \frac{3}{2} x = \frac{8}{7}\)
34. \(− \frac{3}{2} x = − \frac{7}{5}\)
35. \(x + \frac{3}{4} = \frac{5}{9}\)
36. \(x − \frac{1}{9} = − \frac{3}{2}\)
37. \(x − \frac{4}{7} = \frac{7}{8}\)
38. \(x + \frac{4}{9} = − \frac{3}{4}\)
39. \(x + \frac{8}{9} = \frac{2}{3}\)
40. \(x − \frac{5}{6} = \frac{1}{4}\)
41. \(x + \frac{5}{2} = − \frac{9}{8}\)
42. \(x + \frac{1}{2} = \frac{5}{3}\)
43. \(− \frac{8}{5} x = \frac{7}{9}\)
44. \(− \frac{3}{2} x = − \frac{5}{9}\)
45. \(x − \frac{1}{4} = − \frac{1}{8}\)
46. \(x − \frac{9}{2} = − \frac{7}{2}\)
47. \(− \frac{1}{4} x = \frac{1}{2}\)
48. \(− \frac{8}{9} x = − \frac{8}{3}\)
En Ejercicios 49-72, resuelve la ecuación y simplifica tu respuesta.
49. \(− \frac{7}{3} x − \frac{2}{3} = \frac{3}{4} x + \frac{2}{3}\)
50. \(\frac{1}{2} x − \frac{1}{2} = \frac{3}{2} x + \frac{3}{4}\)
51. \(− \frac{7}{2} x − \frac{5}{4} = \frac{4}{5}\)
52. \(− \frac{7}{6} x + \frac{5}{6} = − \frac{8}{9}\)
53. \(− \frac{9}{7} x + \frac{9}{2} = − \frac{5}{2}\)
54. \(\frac{5}{9} x − \frac{7}{2} = \frac{1}{4}\)
55. \(\frac{1}{4} x − \frac{4}{3} = − \frac{2}{3}\)
56. \(\frac{8}{7} x + \frac{3}{7} = \frac{5}{3}\)
57. \(\frac{5}{3} x + \frac{3}{2} = − \frac{1}{4}\)
58. \(\frac{1}{2} x − \frac{8}{3} = − \frac{2}{5}\)
59. \(− \frac{1}{3} x + \frac{4}{5} = − \frac{9}{5} x − \frac{5}{6}\)
60. \(− \frac{2}{9} x − \frac{3}{5} = \frac{4}{5} x − \frac{3}{2}\)
61. \(− \frac{4}{9} x − \frac{8}{9} = \frac{1}{2} x − \frac{1}{2}\)
62. \(− \frac{5}{4} x − \frac{5}{3} = \frac{8}{7} x + \frac{7}{3}\)
63. \(\frac{1}{2} x − \frac{1}{8} = − \frac{1}{8} x + \frac{5}{7}\)
64. \(− \frac{3}{2} x + \frac{8}{3} = \frac{7}{9} x − \frac{1}{2}\)
65. \(− \frac{3}{7} x − \frac{1}{3} = − \frac{1}{9}\)
66. \(\frac{2}{3} x + \frac{2}{9} = − \frac{9}{5}\)
67. \(− \frac{3}{4} x + \frac{2}{7} = \frac{8}{7} x − \frac{1}{3}\)
68. \(\frac{1}{2} x + \frac{1}{3} = − \frac{5}{2} x − \frac{1}{4}\)
69. \(− \frac{3}{4} x − \frac{2}{3} = − \frac{2}{3} x − \frac{1}{2}\)
70. \(\frac{1}{3} x − \frac{5}{7} = \frac{3}{2} x + \frac{4}{3}\)
71. \(− \frac{5}{2} x + \frac{9}{5} = \frac{5}{8}\)
72. \(\frac{9}{4} x + \frac{4}{3} = − \frac{1}{6}\)
73. En un partido de futbol local, los locutores informaron a la multitud que la asistencia al juego fue de 4 mil 302. Si esto es 2/9 de la capacidad, encuentra el aforo completo para el estadio de futbol.
74. En un juego de basquetbol local, los locutores informaron a la multitud que la asistencia al juego fue de 5 mil 394. Si esto es 2/7 de la capacidad, encuentra el aforo completo para el estadio de basquetbol.
75. El área de un triángulo es de 51 pulgadas cuadradas. Si la longitud de la base es\(8 \frac{1}{2}\) pulgadas, encuentra la altura (altitud) del triángulo.
76. El área de un triángulo es de 20 pulgadas cuadradas. Si la longitud de la base es\(2 \frac{1}{2}\) pulgadas, encuentra la altura (altitud) del triángulo.
77. El área de un triángulo es de 18 pulgadas cuadradas. Si la longitud de la base es\(4 \frac{1}{2}\) pulgadas, encuentra la altura (altitud) del triángulo.
78. El área de un triángulo es de 44 pulgadas cuadradas. Si la longitud de la base es\(5 \frac{1}{2}\) pulgadas, encuentra la altura (altitud) del triángulo.
79. En un partido de hockey local, los locutores informaron a la multitud que la asistencia al juego fue de 4 mil 536. Si esto es 2/11 de la capacidad, encuentra el aforo completo para el estadio de hockey.
80. En un partido de futbol local, los locutores informaron a la multitud que la asistencia al juego fue de 6 mil 970. Si esto es 2/7 de la capacidad, encuentra el aforo completo para el estadio de futbol.
81. Piratas. Alrededor de un tercio de los ataques piratas del mundo en 2008 ocurrieron frente a la costa somalí. Si hubo 111 ataques piratas frente a la costa somalí, estime el número de ataques piratas a nivel mundial en 2008.
82. Arsenal nuclear. Estados Unidos y Rusia acordaron recortar los arsenales nucleares de armas nucleares de largo alcance en aproximadamente un tercio, hasta llegar a 1.550. ¿Cuántas armas nucleares de largo alcance hay ahora? Associated Press-Times-Standard 04/04/10 Corazón nuclear ansioso por los cortes de misiles.
83. Bóveda de semillas. La bóveda global de semillas de Svalbard ha acumulado medio millón de muestras de semillas y ahora alberga al menos un tercio de las semillas de cultivo del mundo. Estimar el número total de semillas de cultivo del mundo. Associated Press-Times-Standard 15/03/10 La bóveda de semillas del fin del mundo de Noruega alcanza la marca de medio millón.
84. Tren de carga. El tren Union Pacific de tres millas y media de largo tiene aproximadamente 2 1 2 veces la longitud de un tren de carga típico. ¿Cuánto dura un tren de carga típico? Associated Press-Times-Standard 01/13/10 Tren inútilmente largo plantea preocupaciones de seguridad.
RESPUESTAS
1. No
3. No
5. Sí
7. Sí
9. No
11. Sí
13. \(− \frac{5}{2}\)
15. \(\frac{2}{5}\)
17. \(\frac{4}{11}\)
19. \(\frac{7}{15}\)
21. \(\frac{8}{9}\)
23. \(\frac{10}{13}\)
25. \(−1\)
27. \(− \frac{5}{18}\)
29. \(\frac{64}{21}\)
31. \(− \frac{5}{12}\)
33. \(− \frac{16}{21}\)
35. \(− \frac{7}{36}\)
37. \(\frac{81}{56}\)
39. \(− \frac{2}{9}\)
41. \(− \frac{29}{8}\)
43. \(− \frac{35}{72}\)
45. \(\frac{1}{8}\)
47. \(−2\)
49. \(− \frac{16}{37}\)
51. \(− \frac{41}{70}\)
53. \(\frac{49}{9}\)
55. \(\frac{8}{3}\)
57. \(− \frac{21}{20}\)
59. \(− \frac{49}{44}\)
61. \(− \frac{7}{17}\)
63. \(\frac{47}{35}\)
65. \(− \frac{14}{27}\)
67. \(\frac{52}{159}\)
69. \(− 2\)
71. \(\frac{47}{100}\)
73. 19,359
75. 12
77. 8
79. 24.948
81. Hubo alrededor de 333 ataques piratas en todo el mundo.
83. 1,500,000


