4.6: Multiplicar y dividir fracciones mixtas
- Page ID
- 113456
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Comenzamos con definiciones de fracciones propias e impropias.
Fracciones propias e impropias
Una fracción propia es una fracción cuyo numerador es menor que su denominador. Una fracción impropia es una fracción cuyo numerador es mayor que su denominador.
Por ejemplo,
\[ \frac{2}{3}, ~ - \frac{23}{39}, \text{ and } \frac{ 119}{127}\nonumber \]
son todos ejemplos de fracciones propias. Por otra parte,
\[ \frac{4}{3},~ - \frac{317}{123}, \text{ and } - \frac{233}{101}\nonumber \]
son todos ejemplos de fracciones impropias.
Una fracción mixta 1 es parte número entero, fracción parcial.
Fracciones Mixtas
El número
\[ 5 \frac{3}{4}\nonumber \]
se llama fracción mixta. Se define como
\[5 \frac{3}{4} = 5 + \frac{3}{4}.\nonumber \]
En la fracción mixta\(5 \frac{3}{4}\), el 5 es la parte del número entero y el 3/4 es la parte fraccionaria.
Cambio de fracciones mixtas a fracciones impropias
Tenemos todas las herramientas necesarias para cambiar una fracción mixta en una fracción impropia. Comenzamos con un ejemplo.
Ejemplo 1
Cambiar la fracción mixta\(4 \frac{7}{8}\) en una fracción impropia.
Solución
Empleamos la definición de una fracción mixta, hacemos una fracción equivalente para la parte del número entero, luego agregamos.
\[ \begin{aligned} 4 \frac{7}{8} = 4 + \frac{7}{8} ~ & \textcolor{red}{ \text{ By definition.}} \\ = \frac{4 \cdot \textcolor{red}{8}}{ \textcolor{red}{8}} + \frac{7}{8} ~ & \textcolor{red}{ \text{ Equivalent fraction with LCD = 8.}} \\ = \frac{4 \cdot 8 + 7}{8} ~ & \textcolor{red}{ \text{ Add numerators over common denominator.}} \\ = \frac{39}{8} ~ & \textcolor{red}{ \text{ Simplify the numerator.}} \end{aligned}\nonumber \]
Así,\(4 \frac{7}{8}\) es igual a 39/8.
Ejercicio
Cambiar\(5 \frac{3}{4}\) a una fracción impropia.
- Contestar
-
23/4
Existe una técnica rápida que puedes usar para cambiar una fracción mixta en una fracción impropia.
Manera Rápida de Cambiar una Fracción Mixta a una Fracción Inapropiada
Para cambiar una fracción mixta a una fracción impropia, multiplique la parte del número entero por el denominador, agregue el numerador, luego coloque el resultado sobre el denominador.
Así, para cambiar rápidamente\(4 \frac{7}{8}\) a una fracción impropia, multiplicar el número entero 4 por el denominador 8, sumar el numerador 7, luego colocar el resultado sobre el denominador. En símbolos, esto se vería así:
\[ 4 \frac{7}{8} = \frac{4 \cdot 8 + 7}{8}.\nonumber \]
Así es precisamente como se ve el tercer paso del Ejemplo 1; simplemente estamos eliminando gran parte del trabajo.
Ejemplo 2
Cambiar\(4 \frac{2}{3}\) a una fracción impropia.
Solución
Toma\(4 \frac{2}{3}\), multiplica la parte del número entero por el denominador, suma el numerador, luego pon el resultado sobre el denominador.
\[4 \frac{2}{3} = \frac{4 \cdot 3 + 2}{3}\nonumber \]
Así, el resultado es
\[4 \frac{2}{3} = \frac{14}{3}.\nonumber \]
Ejercicio
Cambiar\(7 \frac{3{8}\) a una fracción impropia.
- Contestar
-
59/8
Es muy fácil hacer el paso intermedio en el Ejemplo 2 mentalmente, permitiéndote saltarte el paso intermedio e ir directamente de la fracción mixta a la fracción impropia sin anotar ni un solo poco de trabajo.
Ejemplo 3
Sin anotar ningún trabajo, utilizar la aritmética mental para cambiar\(-2 \frac{3}{5}\) a una fracción impropia.
Solución
Para cambiar\(−2 \frac{3}{5}\) a una fracción impropia, ignore el signo menos, proceda como antes, luego prefija el signo menos a la fracción impropia resultante. Entonces, multiplica 5 veces 2 y suma 3. Ponga el resultado 13 sobre el denominador 5, luego prefija la fracción impropia resultante con un signo menos. Es decir,
\[-2 \frac{3}{5} = - \frac{13}{5}.\nonumber \]
Ejercicio
Cambiar\(-3 \frac{5}{12}\) a una fracción impropia.
- Contestar
-
−41/12
Cambio de fracciones impropias a fracciones mixtas
El primer paso para cambiar la fracción impropia 27/5 por una fracción mixta es escribir la fracción impropia como suma.
\[\frac{27}{5} = \frac{25}{5} + \frac{2}{5}\nonumber \]
Simplificando la ecuación 4.1, obtenemos
\[ \begin{aligned} \frac{27}{5} = 5 + \frac{2}{5} \\ = 5 \frac{2}{5} \end{aligned}\nonumber \]
Comentario. No se puede simplemente elegir cualquier suma. La suma utilizada en la ecuación 4.1 se construye de manera que la primera fracción sea igual a un número entero y la segunda fracción sea propia. Cualquier otra suma no logrará producir la fracción mixta correcta. Por ejemplo, la suma
\[ \frac{27}{5} = \frac{23}{5} + \frac{4}{5}\nonumber \]
es inútil, porque 23/5 no es un número entero. Asimismo, la suma
\[ \frac{27}{5} = \frac{20}{5} + \frac{7}{5}\nonumber \]
no es bueno. A pesar de que 20/5 = 4 es un número entero, la segunda fracción 7/5 sigue siendo impropia.
Ejemplo 4
Cambiar 25/9 a una fracción mixta.
Solución
Romper 25/9 en la suma correspondiente.
\[ \begin{aligned} \frac{25}{9} = \frac{18}{9} + \frac{7}{9} \\ = 2 + \frac{7}{9} \\ = 2 \frac{7}{9} \end{aligned}\nonumber \]
Ejercicio
Cambiar 25/7 a una fracción mixta.
- Contestar
-
\(3 \frac{4}{7}\).
Comentar. Está surgiendo un patrón. • En el caso de 27/5, tenga en cuenta que 27 dividido por 5 es igual a 5 con un resto de 2. Compare esto con el resultado de la fracción mixta: 27/5=5 2 5. • En el caso del Ejemplo 4, nótese que 25 dividido por 9 es 2 con un resto de 7. Compárelo con el resultado de la fracción mixta: 25/9=2 7 9. Estas observaciones motivan la siguiente técnica.
Manera Rápida de Cambiar una Fracción Inapropiada a una Fracción Mixta
Para cambiar una fracción impropia a una fracción mixta, divida el numerador por el denominador. El cociente será la parte numérica entera de la fracción mixta. Si colocas el resto sobre el denominador, esta será la parte fraccionaria de la fracción mixta.
Ejemplo 5
Cambiar 37/8 a una fracción mixta.
Solución
37 dividido por 8 es 4, con un resto de 5. Es decir:
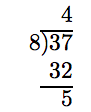
El cociente se convierte en la parte del número entero y ponemos el resto sobre el divisor. Por lo tanto,
\[ \frac{37}{8} = 4 \frac{5}{8}.\nonumber \]
Nota: Puedes verificar tu resultado con la “Manera Rápida de Cambiar una Fracción Mixta a una Fracción Inadecuada”. 8 veces 4 más 5 es 37. Pon esto sobre 8 para obtener 37/8.
Ejercicio
Cambiar 38/9 a una fracción mixta.
- Contestar
-
\(4 \frac{2}{9}\)
Ejemplo 6
Cambiar −43/5 a una fracción mixta.
Solución
Ignorar el signo menos y proceder de la misma manera que en el Ejemplo 5. 43 dividido por 5 es 8, con un resto de 3.
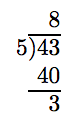
El cociente es la parte del número entero, luego ponemos el resto sobre el divisor. Por último, prefijo el signo menos.
\[ -\frac{43}{5} = -8 \frac{3}{5}\nonumber \]
Multiplicar y dividir fracciones mixtas
Tienes todas las herramientas necesarias para multiplicar y dividir fracciones mixtas. Primero, cambia las fracciones mixtas a fracciones impropias, luego multiplica o divide como hiciste en las secciones anteriores.
1 Una fracción mixta a veces se denomina número mixto.
Ejemplo 7
Simplificar:\(-2 \frac{1}{12} \cdot 2 \frac{4}{5}\).
Solución
Cambiar a fracciones impropias, factorizar, cancelar y simplificar.
\[ \begin{aligned} -2 \frac{1}{12} \cdot 2 \frac{4}{5} = - \frac{25}{12} \cdot \frac{14}{5} ~ & \textcolor{red}{ \text{ Change to improper fractions.}} \\ = - \frac{25 \cdot 14}{12 \cdot 5} ~ & \textcolor{red}{ \begin{aligned} \text{ Multiply numerators; multiply denominators.} \\ \text{ Unlike signs; product is negative.} \end{aligned}} \\ = - \frac{(5 \cdot 5) \cdot (2 \cdot 7)}{2 \cdot 2 \cdot 3) \cdot (5)} ~ & \textcolor{red}{ \text{ Prime factor.}} \\ = - \frac{ \cancel{5} \cdot 5 \cdot \cancel{2} \cdot 7}{ \cancel{2} \cdot 2 \cdot 3 \cdot \cancel{5}} ~ & \textcolor{red}{ \text{ Cancel common factors.}} \\ = - \frac{35}{6} ~ & \textcolor{red}{ \text{ Multiply numerators and denominators.}} \end{aligned}\nonumber \]
Esta es una respuesta perfectamente buena, pero si quieres una respuesta de fracción mixta, 35 dividido por 6 es 5, con un resto de 5. Por lo tanto,
\[ -2 \frac{1}{12} \cdot 2 \frac{4}{5} = -5 \frac{5}{6}.\nonumber \]
Ejercicio\(\PageIndex{1}\)
Simplificar:
\[-3 \frac{3}{4} \cdot 2 \frac{2}{5}\nonumber \]
- Contestar
-
−9
Ejemplo 8
Simplificar:
\[-4 \frac{4}{5} \div 5 \frac{3}{5}.\nonumber \]
Solución
Cambiar a fracciones impropias, invertir y multiplicar, factorizar, cancelar y simplificar.
\[ \begin{aligned} -4 \frac{4}{5} \div 5 \frac{3}{5} = - \frac{24}{5} \div \frac{28}{5} ~ & \textcolor{red}{ \text{ Change to improper fractions.}} \\ = - \frac{24}{5} \cdot \frac{5}{28} ~ & \textcolor{red}{ \text{ Invert and multiply.}} \\ = - \frac{2 \cdot 2 \cdot 2 \cdot 3}{5} \cdot \frac{5}{2 \cdot 2 \cdot 7} ~ & \textcolor{red}{ \text{ Prime factor.}} \\ = - \frac{ \cancel{2} \cdot \cancel{2} \cdot 2 \cdot 3}{ \cancel{3}} \cdot \frac{ \cancel{5}}{ \cancel{2} \cdot \cancel{2} \cdot 7} ~ & \textcolor{red}{ \text{ Cancel common factors.}} \\ = - \frac{6}{7} ~ & \textcolor{red}{ \text{ Multiply numerators and denominators.}} \cdot \end{aligned}\nonumber \]
Ejercicio
Simplificar:
\[-2 \frac{4}{9} \cdot 3 \frac{2}{3}\nonumber \]
- Contestar
-
−2/3
Ejercicios
En los Ejercicios 1-12, convertir la fracción mixta en una fracción impropia.
1. \(2 \frac{1}{3}\)
2. \(1 \frac{8}{11}\)
3. \(1 \frac{1}{19}\)
4. \(−1 \frac{1}{5}\)
5. \(−1 \frac{3}{7}\)
6. \(1 \frac{3}{17}\)
7. \(1 \frac{1}{9}\)
8. \(1 \frac{5}{11}\)
9. \(−1 \frac{1}{2}\)
10. \(−1 \frac{5}{8}\)
11. \(1 \frac{1}{3}\)
12. \(−1 \frac{5}{7}\)
En Ejercicios 13-24, convertir la fracción impropia en una fracción mixta.
13. \(\frac{13}{7}\)
14. \(\frac{−17}{9}\)
15. \(\frac{−13}{5}\)
16. \(\frac{−10}{3}\)
17. \(\frac{−16}{5}\)
18. \(\frac{16}{13}\)
19. \(\frac{9}{8}\)
20. \(\frac{16}{5}\)
21. \(\frac{−6}{5}\)
22. \(\frac{−17}{10}\)
23. \(\frac{−3}{2}\)
24. \(\frac{−7}{4}\)
En Ejercicios 25-48, multiplica los números y expresa tu respuesta como una fracción mixta.
25. \(1 \frac{1}{7} \cdot 2 \frac{1}{2}\)
26. \(1 \frac{1}{8} \cdot 1 \frac{1}{6}\)
27. \(4 \cdot 1 \frac{1}{6}\)
28. \(1 \frac{7}{10} \cdot 4\)
29. \( \left( −1 \frac{1}{12} \right) \left( 3 \frac{3}{4} \right)\)
30. \( \left( −3 \frac{1}{2} \right) \left( 3 \frac{1}{3} \right)\)
31. \(7 \frac{1}{2} \cdot 1 \frac{1}{13}\)
32. \(2 \frac{1}{4} \cdot 1 \frac{5}{11}\)
33. \( \left( 1 \frac{2}{13} \right) \left( −4 \frac{2}{3} \right)\)
34. \( \left( 1 \frac{1}{14} \right) \left( −2 \frac{2}{5} \right)\)
35. \( \left( 1 \frac{3}{7} \right) \left( −3 \frac{3}{4} \right)\)
36. \( \left( 1 \frac{4}{5} \right) \left( −3 \frac{3}{4} \right)\)
37. \(9 \cdot \left( −1 \frac{2}{15} \right)\)
38. \(4 \cdot \left( −2 \frac{5}{6} \right)\)
39. \( \left( −2 \frac{1}{8} \right) (−6)\)
40. \((−9) \left( −3 \frac{1}{6} \right)\)
41. \( \left( −4 \frac{1}{2} \right) \left( −2 \frac{2}{5} \right)\)
42. \( \left( −1 \frac{3}{7} \right) \left( −3 \frac{3}{4} \right)\)
43. \( \left( −2 \frac{1}{6} \right) \cdot 4\)
44. \((−6) \cdot \left( 1 \frac{1}{9} \right)\)
45. \( \left( −1 \frac{4}{15} \right) \left( 2 \frac{1}{2} \right)\)
46. \( \left( −1 \frac{1}{5} \right) \left( 1 \frac{5}{9} \right)\)
47. \( \left( −2 \frac{1}{2} \right) \left( −1 \frac{7}{11} \right)\)
48. \( \left( −1 \frac{7}{11} \right) \left( −1 \frac{7}{12} \right)\)
En los Ejercicios 49-72, divide las fracciones mixtas y expresa tu respuesta como una fracción mixta.
49. \(8 \div 2 \frac{2}{9}\)
50. \(4 \frac{2}{3} \div 4\)
51. \( \left( −3 \frac{1}{2} \right) \div \left( 1 \frac{1}{16} \right)\)
52. \( \left( −1 \frac{2}{5} \right) \div \left( 1 \frac{1}{15} \right)\)
53. \(6 \frac{1}{2} \div 1 \frac{7}{12}\)
54. \(5 \frac{1}{2} \div 1 \frac{9}{10}\)
55. \((−4) \div \left( 1 \frac{5}{9} \right)\)
56. \( \left( −4 \frac{2}{3} \right) \div 4\)
57. \( \left( −5 \frac{2}{3} \right) \div \left( −2 \frac{1}{6} \right)\)
58. \( \left( −2 \frac{1}{2} \right) \div \left( −2 \frac{2}{9} \right)\)
59. \( \left( −6 \frac{1}{2} \right) \div \left( 4 \frac{1}{4} \right)\)
60. \( \left( −1 \frac{1}{6} \right) \div \left( 1 \frac{1}{8} \right)\)
61. \((−6) \div \left( −1 \frac{3}{11} \right)\)
62. \( \left( −6 \frac{2}{3} \right) \div (−6)\)
63. \( \left( 4 \frac{2}{3} \right) \div (−4)\)
64. \( \left( 6 \frac{2}{3} \right) \div (−6)\)
65. \( \left( 1 \frac{3}{4} \right) \div \left( −1 \frac{1}{12} \right)\)
66. \( \left( 2 \frac{4}{7} \right) \div \left( −1 \frac{1}{5} \right)\)
67. \( \left( 5 \frac{2}{3} \right) \div 1 \frac{1}{9}\)
68. \( 1 \frac{2}{3} \div 1 \frac{2}{9}\)
69. \( \left( −7 \frac{1}{2} \right) \div \left( −2 \frac{2}{5} \right)\)
70. \( \left( −5 \frac{1}{3} \right) \div \left( −2 \frac{5}{6} \right)\)
71. \( \left( 3 \frac{2}{3} \right) \div \left( −1 \frac{1}{9} \right)\)
72. \( \left( 8 \frac{1}{2} \right) \div \left( −1 \frac{3}{4} \right)\)
73. Lotes Pequeños. ¿Cuántos lotes de cuarto de acre se pueden hacer con\(6 \frac{1}{2}\) acres de tierra?
74. Campo Grande. Se formó un campo a partir de lotes de\(17 \frac{1}{2}\) medio acre. ¿Cuántos acres fue el campo resultante?
75. Joyería. Para hacer algunas joyas, se cortó una barra de plata de\(4 \frac{1}{2}\) pulgadas de largo en trozos de\( \frac{1}{12}\) pulgada de largo. ¿Cuántas piezas se hicieron?
76. Muffins. Esta receta hará 6 magdalenas: 1 taza de leche,\(1 \frac{2}{3}\) tazas de harina, 2 huevos, 1/2 cucharadita de sal,\(1 \frac{1}{2}\) cucharaditas de polvo de hornear. Escribe la receta de seis docenas de magdalenas.
RESPUESTAS
1. \( \frac{7}{3}\)
3. \( \frac{20}{19}\)
5. \(− \frac{10}{7}\)
7. \( \frac{10}{9}\)
9. \(− \frac{3}{2}\)
11. \( \frac{4}{3}\)
13. \(1 \frac{6}{7}\)
15. \(−2 \frac{3}{5}\)
17. \(−3 \frac{1}{5}\)
19. \(1 \frac{1}{8}\)
21. \(−1 \frac{1}{5}\)
23. \(−1 \frac{1}{2}\)
25. \(2 \frac{6}{7}\)
27. \(4 \frac{2}{3}\)
29. \(−4 \frac{1}{16}\)
31. \(8 \frac{1}{13}\)
33. \(−5 \frac{5}{13}\)
35. \(−5 \frac{5}{14}\)
37. \(−10 \frac{1}{5}\)
39. \(12 \frac{3}{4}\)
41. \(10 \frac{4}{5}\)
43. \(− 8 \frac{2}{3}\)
45. \(− 3 \frac{1}{6}\)
47. \(4 \frac{1}{11}\)
49. \(3 \frac{3}{5}\)
51. \(− 3 \frac{5}{17}\)
53. \(4 \frac{2}{19}\)
55. \(− 2 \frac{4}{7}\)
57. \(2 \frac{8}{13}\)
59. \(− 1 \frac{9}{17}\)
61. \(4 \frac{5}{7}\)
63. \(− 1 \frac{1}{6}\)
65. \(− 1 \frac{8}{13}\)
67. \(5 \frac{1}{10}\)
69. \(3 \frac{1}{8}\)
71. \(− 3 \frac{3}{10}\)
73. 26 lotes de cuarto de acre
75. 54 piezas


