4.3: Multiplicar fracciones
- Page ID
- 113452
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Considere la imagen en la Figura 4.5, donde las líneas verticales dividen la región rectangular en tres piezas iguales. Si sombreamos una de las tres piezas iguales, el área sombreada representa 1/3 de toda la región rectangular.

Nos gustaría visualizar tomando 1/2 de 1/3. Para ello, dibujamos una línea horizontal adicional que divide la región sombreada por la mitad horizontalmente. Esto se muestra en la Figura 4.6. La región sombreada que representaba 1/3 ahora se divide en dos regiones rectangulares más pequeñas, una de las cuales está sombreada con un color diferente. Esta región representa 1/2 de 1/3.

A continuación, extender la línea horizontal todo el ancho de la región rectangular, como se muestra en la Figura 4.7.

Tenga en cuenta que dibujar la línea horizontal, junto con las tres líneas verticales originales, ha logrado dividir la región rectangular completa en seis piezas más pequeñas pero iguales, solo una de las cuales (la que representa 1/2 de 1/3) está sombreada en un nuevo color. De ahí que esta pieza recién sombreada representa 1/6 de toda la región. La conclusión de nuestro argumento visual es el hecho de que 1/2 de 1/3 equivale a 1/6. En símbolos,
\[ \frac{1}{2} \cdot \frac{1}{3} = \frac{1}{6} .\nonumber \]
Ejemplo 1
Crea un argumento visual que muestre que 1/3 de 2/5 es 2/15.
Solución
Primero, divida una región rectangular en cinco piezas iguales y sombree dos de ellas. Esto representa la fracción 2/5.
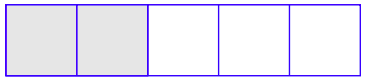
A continuación, dibuje dos líneas horizontales que dividen la región sombreada en tres piezas iguales y sombrean 1 de las tres piezas iguales. Esto representa tomar 1/3 de 2/5.
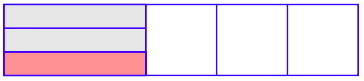
A continuación, extiende las líneas horizontales todo el ancho de la región y devuelve la línea vertical original desde la primera imagen.
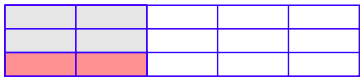
Obsérvese que las tres líneas horizontales, aunadas a las cinco líneas verticales originales, han logrado dividir toda la región en 15 piezas más pequeñas pero iguales, de las cuales sólo dos (las que representan 1/3 de 2/5) están sombreadas en el nuevo color. De ahí que esta pieza recién sombreada representa 2/15 de toda la región. La conclusión de este argumento visual es el hecho de que 1/3 de 2/5 equivale a 2/15. En símbolos,
\[ \frac{1}{3} \cdot \frac{2}{5} = \frac{2}{15}.\nonumber \]
Ejercicio
Crea un argumento visual que muestre que 1/2 de 1/4 es 1/8.
- Contestar
-
Diagrama:

Regla de multiplicación
En la Figura 4.7, vimos que 1/2 de 1/3 equivale a 1/6. Observe lo que sucede cuando multiplicamos los numeradores y multiplicamos los denominadores de las fracciones 1/2 y 1/3.
\[ \begin{aligned} \frac{1}{2} \cdot \frac{1}{3} = \frac{1 \cdot 1}{2 \cdot 3} ~ & \textcolor{red}{ \text{ Multiply numerators; multiply denominators.}} \\ = \frac{1}{6} ~ & \textcolor{red}{ \text{ Simplify numerators and denominators.}} \end{aligned}\nonumber \]
¡Obtenemos 1/6!
¿Podría ser esto una coincidencia o suerte? Intentemos eso nuevamente con las fracciones del Ejemplo 1, donde vimos que 1/3 de 2/5 equivale a 2/15. Nuevamente, multiplicar los numeradores y denominadores de 1/3 y 2/5.
\[ \begin{aligned} \frac{1}{3} \cdot \frac{2}{5} = \frac{1 \cdot 2}{3 \cdot 5} ~ & \textcolor{red}{ \text{ Multiply numerators; multiply denominators.}} \\ = \frac{2}{15} ~ & \textcolor{red}{ \text{ Simplify numerators and denominators.}} \end{aligned}\nonumber \]
De nuevo, ¡obtenemos 2/15!
Estos dos ejemplos motivan la siguiente definición.
Definición: Regla de multiplicación
Para encontrar el producto de las fracciones a/b y c/d, multiplique sus numeradores y denominadores. En símbolos,
\[ \frac{a}{b} \cdot \frac{c}{d} = \frac{a \cdot c}{b \cdot d}\nonumber \]
Ejemplo 2
Multiplica 1/5 y 7/9.
Solución
Multiplicar numeradores y multiplicar denominadores.
\[ \begin{aligned} \frac{1}{5} \cdot \frac{7}{9} = \frac{1 \cdot 7}{5 \cdot 9} ~ & \textcolor{red}{ \text{ Multiply numerators; multiply denominators.}} \\ = \frac{7}{45} ~ & \textcolor{red}{ \text{ Simplify numerators and denominators.}} \end{aligned}\nonumber \]
Ejercicio
Multiplicar:
\[ \frac{1}{3} \cdot \frac{2}{5}\nonumber \]
- Contestar
-
Multiplicar:\( \frac{6}{15}\)
Ejemplo 3
Encuentra el producto de −2/3 y 7/9.
Solución
Las reglas habituales de los signos se aplican a los productos. A diferencia de los signos arrojan un resultado negativo.
\[ \begin{aligned} - \frac{2}{3} \cdot \frac{7}{9} = - \frac{2 \cdot 7}{3 \cdot 9} & \textcolor{red}{ \text{ Multiply numerators; multiply denominators.}} \\ = - \frac{14}{27} ~ & \textcolor{red}{ \text{ Simplify numerators and denominators.}} \end{aligned}\nonumber \]
No se requiere que muestres físicamente el paso medio. Si quieres hacerlo mentalmente, entonces simplemente puedes escribir
\[ - \frac{2}{3} \cdot \frac{7}{9} = - \frac{14}{27}.\nonumber \]
Ejercicio
Multiplicar:
\[ - \frac{3}{5} \cdot \frac{2}{7}\nonumber \]
- Contestar
-
\[ - \frac{6}{35}\nonumber \]
Multiplicar y reducir
Después de multiplicar dos fracciones, asegúrate de que tu respuesta se reduzca a los términos más bajos (ver Sección 4.1).
Ejemplo 4
Multiplicar 3/4 veces 8/9.
Solución
Después de multiplicar, divide el numerador y el denominador por el mayor divisor común del numerador y denominador.
\[ \begin{aligned} \frac{3}{4} \cdot \frac{8}{9} = \frac{3 \cdot 8}{4 \cdot 9} ~ & \textcolor{red}{ \text{ Multiply numerators and denominators.}} \\ = \frac{24}{36} ~ & \textcolor{red}{ \text{ Simplify numerator and denominator.}} \\ = \frac{24 \div 12}{36 \div 12} ~ & \textcolor{red}{ \text{ Divide numerator and denominator by GCD.}} \\ = \frac{2}{3} ~ & \textcolor{red}{ \text{ Simplify numerator and denominator.}} \end{aligned}\nonumber \]
Alternativamente, después de multiplicar, puede factorizar tanto el numerador como el denominador, luego cancelar los factores comunes.
\[ \begin{aligned} \frac{3}{4} \cdot \frac{8}{9} = \frac{24}{36} ~ & \textcolor{red}{ \text{ Multiply numerators and denominators.}} \\ = \frac{2 \cdot 2 \cdot 2 \cdot 3}{2 \cdot 2 \cdot 3 \cdot 3} ~ & \textcolor{red}{ \text{ Prime factor numerator and denominator.}} \\ = = \frac{\cancel{2} \cdot \cancel{2} \cdot 2 \cdot \cancel{3}}{\cancel{2} \cdot \cancel{2} \cdot 3 \cdot \cancel{3}} ~ & \textcolor{red}{ \text{ Cancel common factors.}} \\ = \frac{2}{3} ~ \end{aligned}\nonumber \]
Ejercicio
Multiplicar:
\[ \frac{3}{7} \cdot \frac{14}{9}\nonumber \]
- Contestar
-
\[ \frac{2}{3}\nonumber \]
Ejemplo 5
Multiplica −7x/2 y 5/ (14x 2).
Solución
Después de multiplicar, factor primo tanto numerador como denominador, luego cancelar factores comunes. Tenga en cuenta que a diferencia de los signos produce un producto negativo.
\[ \begin{aligned} - \frac{7x}{2} \cdot \frac{5}{14x^2} = - \frac{35x}{28x^2} ~ & \textcolor{red}{ \text{ Multiply numerators and denominators.}} \\ = - \frac{5 \cdot 7 \cdot x}{2 \cdot 2 \cdot 7 \cdot x \cdot x} ~ & \textcolor{red}{ \text{ Prime factor numerator and denominator.}} \\ = - \frac{5 \cdot \cancel{7} \cdot \cancel{x}}{2 \cdot 2 \cdot \cancel{7} \cdot \cancel{x} \cdot x} ~ & \textcolor{red}{ \text{ Cancel common factors.}} \\ = - \frac{5}{4x} \end{aligned}\nonumber \]
Ejercicio
Multiplicar:
\[ - \frac{3x}{2} \cdot \frac{6}{21x^3}\nonumber \]
- Contestar
-
\[ - \frac{3}{7x^2}\nonumber \]
Multiplicar y cancelar o cancelar y multiplicar
Cuando se trabaja con números más grandes, se vuelve un poco más difícil de multiplicar, factorizar y cancelar. Considera el siguiente argumento.
\[ \begin{aligned} \frac{18}{30} \cdot \frac{35}{6} = \frac{630}{180} ~ & \textcolor{red}{ \text{ Multiply numerators; multiply denominators.}} \\ = \frac{2 \cdot 3 \cdot 3 \cdot 5 \cdot 7}{2 \cdot 2 \cdot 3 \cdot 3 \cdot 5} ~ & \textcolor{red}{ \text{ Prime factor numerators and denominators.}} \\ = \frac{ \cancel{2} \cdot \cancel{3} \cdot \cancel{3} \cdot \cancel{5} \cdot 7}{2 \cdot \cancel{2} \cdot \cancel{3} \cdot \cancel{3} \cdot \cancel{5}} ~ & \textcolor{red}{ \text{ Cancel common factors.}} \\ = \frac{7}{2} ~ & \textcolor{red}{ \text{ Remaining factors.}} \end{aligned}\nonumber \]
Hay una serie de dificultades con este enfoque. Primero, hay que multiplicar números grandes, y en segundo lugar, hay que factorizar los resultados aún mayores.
Una posible alternativa es no molestarse en multiplicar numeradores y denominadores, dejándolos en forma factorizada.
\[ \begin{aligned} \frac{18}{30} \cdot \frac{35}{6} = \frac{18 \cdot 35}{30 \cdot 6} ~ & \textcolor{red}{ \text{ Multiply numerators; multiply denominators.}} \end{aligned}\nonumber \]
Encontrar la factorización principal de estos factores más pequeños es más fácil.
\[ \begin{aligned} = \frac{(2 \cdot 3 \cdot 3) \cdot (5 \cdot 7)}{(2 \cdot 3 \cdot 5) \cdot (2 \cdot 3)} ~ & \textcolor{red}{ \text{ Prime factor.}} \end{aligned}\nonumber \]
Ahora podemos cancelar factores comunes. Ya no se necesitan paréntesis en el numerador y denominador porque ambos contienen un producto de factores primos, por lo que el orden y la agrupación no importan.
\[ \begin{aligned} = \frac{ \cancel{2} \cdot \cancel{3} \cdot \cancel{3} \cdot \cancel{5} \cdot \cancel{7}}{ \cancel{2} \cdot \cancel{3} \cdot \cancel{5} \cdot 2 \cdot \cancel{3}} ~ & \textcolor{red}{ \text{ Cancel common factors.}} \\ = \frac{7}{2} ~ & \textcolor{red}{ \text{ Remaining factors.}} \end{aligned}\nonumber \]
Otro enfoque es factorizar numeradores y denominadores en su lugar, cancelar factores comunes, luego multiplicar.
\[ \begin{aligned} \frac{18}{30} \cdot \frac{35}{6} = \frac{2 \cdot 3 \cdot 3}{2 \cdot 3 \cdot 5} \cdot \frac{5 \cdot 7}{2 \cdot 3} ~ & \textcolor{red}{ \text{ Factor numerators and denominators.}} \\ = \frac{ \cancel{2} \cdot \cancel{3} \cdot \cancel{3} \cdot \cancel{3}}{ \cancel{2} \cdot \cancel{3} \cdot \cancel{5}} \cdot \frac{ \cancel{5} \cdot 7}{2 \cdot \cancel{3}} ~ & \textcolor{red}{ \text{ Cancel common factors.}} \\ = \frac{7}{2} ~ & \textcolor{red}{ \text{ Remaining factors.}} \end{aligned}\nonumber \]
Tenga en cuenta que esto arroja exactamente el mismo resultado, 7/2.
Regla de Cancelación
Al multiplicar fracciones, cancele los factores comunes de acuerdo con la siguiente regla: “Cancelar un factor en un numerador por un factor idéntico en un denominador”.
Ejemplo 6
Encuentre el producto de 14/15 y 30/140.
Solución
Multiplicar numeradores y multiplicar denominadores. Factor primo, cancelar factores comunes, luego multiplicar.
\[ \begin{aligned} \frac{14}{15} \cdot \frac{30}{140} = \frac{14 \cdot 30}{15 \cdot 140} ~ & \textcolor{red}{ \text{ Multiply numerators; multiply denominators.}} \\ = \frac{(2 \cdot 7) \cdot (2 \cdot 3 \cdot 5)}{(3 \cdot 5) \cdot (2 \cdot 2 \cdot 5 \cdot 7)} ~ & \textcolor{red}{ \text{ Prime factor numerators and denominators.}} \\ = \frac{ \cancel{2} \cdot \cancel{7} \cdot \cancel{2} \cdot \cancel{3} \cdot \cancel{5}}{ \cancel{3} \cdot 5 cdot \cancel{2} \cdot \cancel{2} \cdot \cancel{5} \cdot \cancel{7}} ~ & \textcolor{red}{ \text{ Cancel common factors.}} \\ = \frac{1}{5} ~ & \textcolor{red}{ \text{ Multiply.}} \end{aligned}\nonumber \]
Nota: Todo en el numerador cancela porque has dividido el numerador por sí mismo. De ahí que la respuesta tenga un 1 en su numerador.
Ejercicio
Multiplicar:
\[ \frac{6}{35} \cdot \frac{70}{36}\nonumber \]
- Contestar
-
\(\frac{1}{3}\)
Cuando todo se cancela
Cuando todos los factores en el numerador cancelan, esto significa que estás dividiendo el numerador por sí mismo. De ahí que te quedes con un 1 en el numerador. La misma regla se aplica al denominador. Si todo en el denominador se cancela, te quedas con un 1 en el denominador.
Ejemplo 7
Simplifica el producto:\ (-\ frac {6x} {55y}\ cdot\ left (-\ frac {110y^2} {105x^2}\ right). \ nonumber\]
Solución
El producto de dos negativos es positivo.
\[ \begin{aligned} - \frac{6x}{55y} \cdot \left( - \frac{110y^2}{105x^2} \right) = \frac{6x}{55y} \cdot \frac{110y^2}{105x^2} ~ & \textcolor{red}{ \text{ Like signs gives a positive.}} \end{aligned}\nonumber \]
Numeradores y denominadores de factores primos, luego cancelan los factores comunes.
\[ \begin{aligned} = \frac{2 \cdot 3 \cdot x}{5 \cdot 11 \cdot y} \cdot \frac{2 \cdot 5 \cdot 11 \cdot y \cdot y}{3 \cdot 5 \cdot 7 \cdot x \cdot x} ~ & \textcolor{red}{ \text{ Prime factor numerators & denominators.}} \\ = \frac{2 \cdot \cancel{3} \cdot \cancel{x}}{5 \cdot \cancel{11} \cdot \cancel{y}} \cdot \frac{2 \cdot \cancel{5} \cdot \cancel{11} \cdot \cancel{y} \cdot y}{ \cancel{3} \cdot \cancel{5} \cdot 7 \cdot \cancel{x} \cdot x} ~ & \textcolor{red}{ \text{ Cancel common factors.}} \\ = \frac{2 \cdot 2 \cdot y}{5 \cdot 7 \cdot x} ~ & \textcolor{red}{ \text{ Remaining factors.}} \\ = \frac{4y}{35x} ~ & \textcolor{red}{ \text{ Multiply numerators; multiply denominators.}} \end{aligned}\nonumber \]
Ejercicio
Simplificar:
\[ \frac{6x}{15b} \cdot \left( - \frac{35b^2}{10a^2} \right)\nonumber \]
- Contestar
-
\[ - \frac{21b}{5a}\nonumber \]
Paralelogramos
En esta sección, vamos a aprender a encontrar el área de un paralelogramo. Comencemos con la definición de un paralelogramo. Recordemos que un cuadrilátero es un polígono que tiene cuatro lados. Un paralelogramo es un tipo muy especial de cuadrilátero.
Paralelogramo
Un paralelogramo es un cuadrilátero cuyos lados opuestos son paralelos.
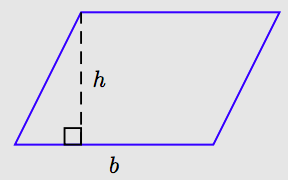
Al lado sobre el que descansa el paralelogramo se le llama su base (etiquetada b en la figura) y la distancia desde su base hasta el lado opuesto se llama su altura (etiquetada h en la figura). Tenga en cuenta que la altitud es perpendicular a la base (se encuentra con la base en un ángulo de 90◦).
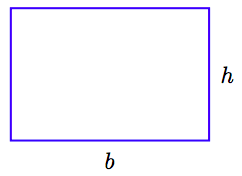
La Figura 4.8 muestra un rectángulo que tiene longitud b y ancho h. Por lo tanto, el área del rectángulo en la Figura 4.8 es A = bh, la cual se encuentra tomando el producto del largo y ancho. Tome un par de tijeras y corte un triángulo desde el extremo derecho del rectángulo como se muestra en la Figura 4.9 (a), luego pegue el triángulo cortado al extremo izquierdo como se muestra en la Figura 4.9 (b). El resultado, visto en la Figura 4.9 (b), es un paralelogramo que tiene base b y altura h.
Debido a que no hemos tirado ningún material al crear el paralelogramo del rectángulo, el paralelogramo tiene la misma área que el rectángulo original. Es decir, el área del paralelogramo es A = bh.
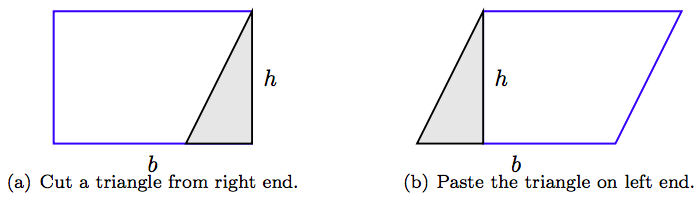
Área de un paralelogramo
Un paralelogramo que tiene base b y altura h tiene área A = bh. Es decir, para encontrar el área de un paralelogramo, tomar el producto de su base y altura.
Ejemplo 8
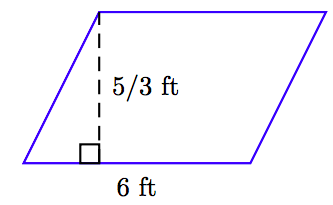
Encuentra el área del paralelogramo que se muestra a continuación.
Solución
El área del paralelogramo es igual al producto de su base y altura. Es decir,
\[ \begin{aligned} A = bh ~ & \textcolor{red}{ \text{ Area formula for a parallelogram.}} \\ = (6 \text{ ft}) \left( \frac{5}{3} \text{ ft} \right) ~ & \textcolor{red}{ \text{ Substitute: 6 ft for }b, \text{ 5/3 ft for } h.} \\ = \frac{30}{3} \text{ ft}^2. ~ & \textcolor{red}{ \text{ Multiply numerators and denominators.}} \\ = 10 \text{ ft}^2. ~ & \textcolor{red}{ \text{ Divide.}} \end{aligned}\nonumber \]
Así, el área del paralelogramo es de 10 pies cuadrados.
Ejercicio
La base de un paralelogramo mide 14 pulgadas. La altura es de 8/7 de pulgada. ¿Cuál es el área del paralelogramo?
- Contestar
-
16 pulgadas cuadradas
Triángulos
Volvamos nuestra atención a aprender a encontrar el área de un triángulo.
Triángulo
Un triángulo es un polígono de tres lados. Se forma trazando tres puntos y conectándolos con tres segmentos de línea. A cada uno de los tres puntos se le llama vértice del triángulo y a cada uno de los tres segmentos de línea se le llama lado del triángulo.
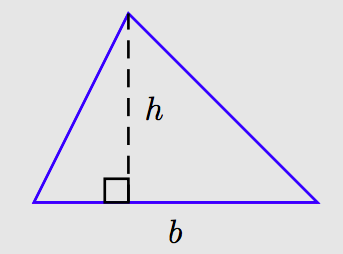
El lado sobre el que descansa el triángulo se llama su base, y la distancia entre su base y vértice opuesto se llama su altura de altitud. La altitud siempre es perpendicular a la base; es decir, forma un ángulo de 90◦ con la base.
Se ve fácilmente que un triángulo tiene la mitad del área de un paralelogramo.
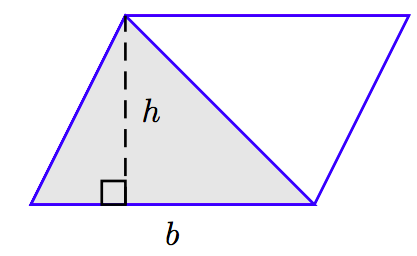
El paralelogramo tiene área A = bh. Por lo tanto, el triángulo tiene la mitad de esa área. Es decir, el área del triángulo es A = (1/2) bh.
Área de un Triángulo
Un triángulo que tiene base b y altura h tiene área A = (1/2) bh. Es decir, para encontrar el área de un triángulo, tomar la mitad del producto de la base y la altura.
Ejemplo 9
Encuentra el área del triángulo que se muestra a continuación.
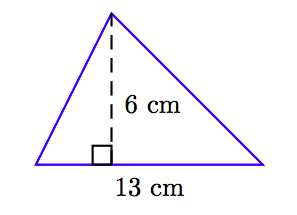
Solución
Para encontrar el área del triángulo, toma la mitad del producto de la base y la altura.
\[ \begin{aligned} A = \frac{1}{2} bh ~ & \textcolor{red}{ \text{ Area of a triangle formula.}} \\ = \frac{1}{2} (13 \text{ cm}) (6 \text{ cm}) ~ & \textcolor{red}{ \text{ Substitute: 13 cm for } b,~ \text{6 cm for } h.} \\ = \frac{78 \text{ cm}^2}{2} ~ & \textcolor{red}{ \text{ Multiply numerators; multiply denominators.}} \\ = 39 \text{ cm}^2. ~ & \textcolor{red}{ \text{ Simplify.}} \end{aligned}\nonumber \]
Por lo tanto, el área del triángulo es de 39 centímetros cuadrados.
Ejercicio
La base de un triángulo mide 15 metros. La altura es de 12 metros. ¿Cuál es el área del triángulo?
- Contestar
-
90 metros cuadrados
Identificar la Base y Altitud
A veces puede ser un poco difícil determinar la base y la altitud (altura) de un triángulo. Por ejemplo, considere el triángulo en la Figura 4.10 (a). Digamos que elegimos el borde inferior del triángulo como base y denotamos su longitud con la variable b, como se muestra en la Figura 4.10 (a).
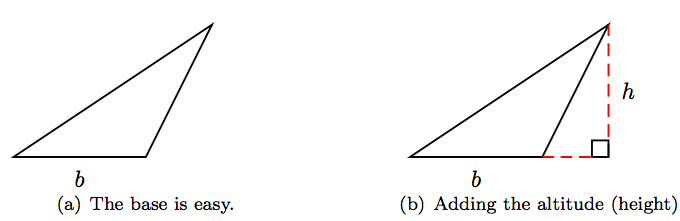
La altitud (altura) del triángulo se define como la distancia entre la base del triángulo y su vértice opuesto. Para identificar esta altitud, primero debemos extender la base, como se ve en la extensión discontinua en la Figura 4.10 (b), luego dejar caer una línea discontinua perpendicular desde el vértice opuesto a la base extendida, también mostrada en la Figura 4.10 (b). Esta perpendicular es la altitud (altura) del triángulo y denotamos su longitud por h.
Pero podemos ir más allá. Cualquiera de los tres lados de un triángulo puede ser designado como la base del triángulo. Supongamos que, como se muestra en la Figura 4.11 (a), identificamos un lado diferente como la base, con longitud denotada por la variable b.
La altitud a esta nueva base será un segmento desde el vértice opuesto, perpendicular a la base. Su longitud en la Figura 4.11 (b) se denota por h.
De igual manera, hay un tercer lado del triángulo que también podría usarse como base. La altitud a este tercer lado se encuentra al caer una perpendicular desde el vértice del triángulo directamente opuesto a esta base. Esto también requeriría extender la base. Dejamos esto a nuestros lectores para que lo exploren.
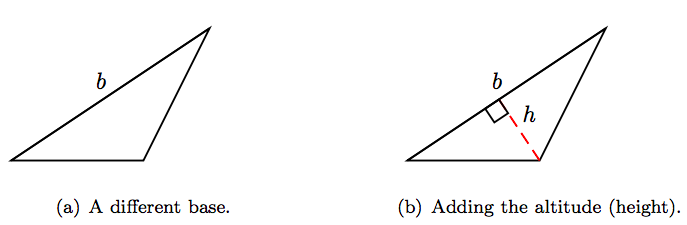
Punto Clave
Cualquiera de los tres lados de un triángulo puede ser utilizado como base. La altitud se dibuja dejando caer una perpendicular desde el vértice opuesto a la base elegida. Esto a veces requiere que extendamos la base. Independientemente del lado que usemos para la base, la fórmula A = bh /2 producirá el mismo resultado de área.
Ejercicios
1. Crear un diagrama, como el que se muestra en la Figura 4.7, para mostrar que 1/3 de 1/3 es 1/9.
2. Crear un diagrama, como el que se muestra en la Figura 4.7, para mostrar que 1/2 de 1/4 es 1/8.
3. Crear un diagrama, como el que se muestra en la Figura 4.7, para mostrar que 1/3 de 1/4 es 1/12.
4. Crear un diagrama, como el que se muestra en la Figura 4.7, para mostrar que 2/3 de 1/3 es 2/9.
En Ejercicios 1-28, multiplica las fracciones, y simplifica tu resultado.
5. \(\frac{−21}{4} \cdot \frac{22}{19}\)
6. \(\frac{−4}{19} \cdot \frac{21}{8}\)
7. \(\frac{20}{11} \cdot \frac{−17}{22}\)
8. \(\frac{−9}{2} \cdot \frac{6}{7}\)
9. \(\frac{21}{8} \cdot \frac{−14}{15}\)
10. \(\frac{−17}{18} \cdot \frac{−3}{4}\)
11. \(\frac{−5}{11} \cdot \frac{7}{20}\)
12. \(\frac{−5}{2} \cdot \frac{−20}{19}\)
13. \(\frac{8}{13} \cdot \frac{−1}{6}\)
14. \(\frac{−12}{7} \cdot \frac{5}{9}\)
15. \(\frac{2}{15} \cdot \frac{−9}{8}\)
16. \(\frac{2}{11} \cdot \frac{−21}{8}\)
17. \(\frac{17}{12} \cdot \frac{3}{4}\)
18. \(\frac{7}{13} \cdot \frac{10}{21}\)
19. \(\frac{−6}{23} \cdot \frac{9}{10}\)
20. \(\frac{12}{11} \cdot \frac{−5}{2}\)
21. \(\frac{−23}{24} \cdot \frac{−6}{17}\)
22. \(\frac{4}{9} \cdot \frac{−21}{19}\)
23. \(\frac{24}{7} \cdot \frac{5}{2}\)
24. \(\frac{−20}{23} \cdot \frac{−1}{2}\)
25. \(\frac{1}{2} \cdot \frac{−8}{11}\)
26. \(\frac{−11}{18} \cdot \frac{−20}{3}\)
27. \(\frac{−24}{13} \cdot \frac{−7}{18}\)
28. \(\frac{21}{20} \cdot \frac{−4}{5}\)
En los Ejercicios 29-40, multiplica las fracciones, y simplifica tu resultado.
29. \(\frac{−12y^3}{13} \cdot \frac{2}{9y^6}\)
30. \(\frac{−8x^3}{3} \cdot \frac{−6}{5x^5}\)
31. \(\frac{11y^3}{24} \cdot \frac{6}{5y^5}\)
32. \(\frac{11y}{18} \cdot \frac{21}{17y^6}\)
33. \(\frac{−8x^2}{21} \cdot \frac{−18}{19x}\)
34. \(\frac{2y^4}{11} \cdot \frac{−7}{18y}\)
35. \(\frac{13x^6}{15} \cdot \frac{9}{16x^2}\)
36. \(\frac{−22x^6}{15} \cdot \frac{17}{16x^3}\)
37. \(\frac{−6y^3}{5} \cdot \frac{−20}{7y^6}\)
38. \(\frac{−21y}{5} \cdot \frac{−8}{3y^2}\)
39. \(\frac{−3y^3}{4} \cdot \frac{23}{12y}\)
40. \(\frac{−16y^6}{15} \cdot \frac{−21}{13y^4}\)
En los Ejercicios 41-56, multiplica las fracciones, y simplifica tu resultado.
41. \(\frac{13y^6}{20x^4} \cdot \frac{2x}{7y^2}\)
42. \(\frac{−8y^3}{13x^6} \cdot \frac{7x^2}{10y^2}\)
43. \(\frac{23y^4}{21x} \cdot \frac{−7x^6}{4y^2}\)
44. \(\frac{−2x^6}{9y^4} \cdot \frac{y^5}{20x}\)
45. \(\frac{11y^6}{12x^6} \cdot \frac{−2x^4}{7y^2}\)
46. \(\frac{16x^3}{13y^4} \cdot \frac{11y^2}{18x}\)
47. \(\frac{x^6}{21y^3} \cdot \frac{−7y^4}{9x^5}\)
48. \(\frac{−3y^3}{5x} \cdot \frac{14x^5}{15y^2}\)
49. \(\frac{19y^2}{18x} \cdot \frac{10x^3}{7y^3}\)
50. \(\frac{−20x}{9y^3} \cdot \frac{−y^6}{4x^3}\)
51. \(\frac{−4y^3}{5x^5} \cdot \frac{−10x}{21y^4}\)
52. \(\frac{11y^2}{14x^4} \cdot \frac{−22x}{21y^3}\)
53. \(\frac{−16x}{21y^2} \cdot \frac{−7y^3}{5x^2}\)
54. \(\frac{−4y}{5x} \cdot \frac{10x^3}{7y^6}\)
55. \(\frac{17x^3}{3y^6} \cdot \frac{−12y^2}{7x^4}\)
56. \(\frac{−6x^4}{11y^3} \cdot \frac{13y^2}{8x^5}\)
En los Ejercicios 57-62, encuentra el área del paralelogramo que tiene la base y altitud dadas.
57. base = 8 cm, altitud = 7 cm
58. base = 2 cm, altitud = 11 cm
59. base = 6 cm, altitud = 13 cm
60. base = 2 cm, altitud = 6 cm
61. base = 18 cm, altitud = 14 cm
62. base = 20 cm, altitud = 2 cm
En Ejercicios 63-68, encuentra el área del triángulo que se muestra en la figura. (Nota: Las figuras no están dibujadas a escala.)
63.
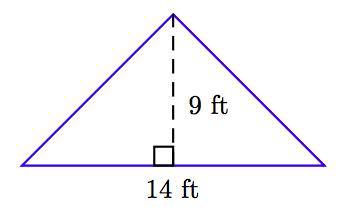
64.
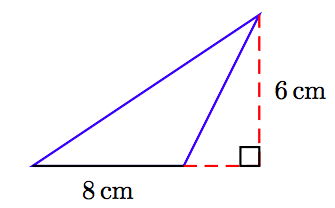
65.
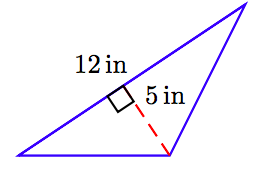
66.
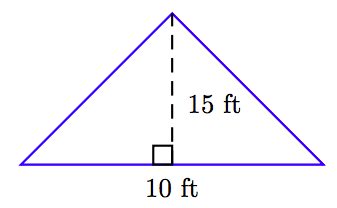
67.
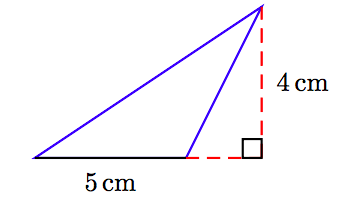
68.
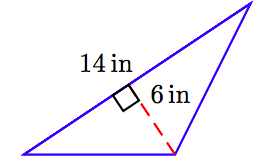
69. Peso en la Luna. En la luna, solo pesarías 1/6 de lo que pesas en la tierra. Si pesas 138 libras en la tierra, ¿cuál sería tu peso en la luna?
RESPUESTAS
1. Esto demuestra que 1/3 de 1/3 es 1/9.

3. Esto demuestra que 1/3 de 1/4 es 1/12.
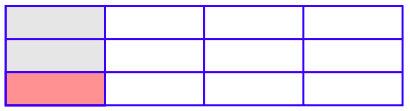
5. \(\frac{−231}{38}\)
7. \(\frac{−170}{121}\)
9. \(\frac{−49}{20}\)
11. \(\frac{−7}{44}\)
13. \(\frac{−4}{39}\)
15. \(\frac{−3}{20}\)
17. \(\frac{17}{16}\)
19. \(\frac{−27}{115}\)
21. \(\frac{23}{68}\)
23. \(\frac{60}{7}\)
25. \(\frac{−4}{11}\)
27. \(\frac{28}{39}\)
29. \(− \frac{8}{39y^3}\)
31. \(\frac{11}{20y^2}\)
33. \(\frac{48x}{133}\)
35. \(\frac{39x^4}{80}\)
37. \(\frac{24}{7y^3}\)
39. \(− \frac{23y^2}{16}\)
41. \(\frac{13y^4}{70x^3}\)
43. \(− \frac{23y^2x^5}{12}\)
45. \(− \frac{11y^4}{42x^2}\)
47. \(− \frac{xy}{27}\)
49. \(\frac{95x^2}{63y}\)
51. \(\frac{8}{21yx^4}\)
53. \(\frac{16y}{15x}\)
55. \(− \frac{68}{7xy^4}\)
57. 56 cm 2
59. 78 cm 2
61. 252 cm 2
63. 63 ft 2
65. 30 en 2
67. 10 cm 2
69. 23 libras


