4.4: Dividir fracciones
- Page ID
- 113450
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Supongamos que tienes cuatro pizzas y cada una de las pizzas se ha cortado en ocho rebanadas iguales. Por lo tanto, cada rebanada de pizza representa 1/8 de una pizza entera.
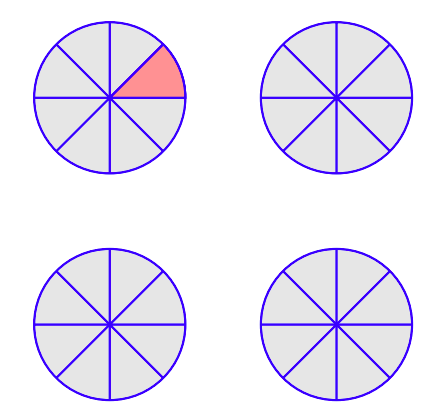
Ahora para la pregunta: ¿Cuántos octavos hay en cuatro? Esta es una declaración de división. Para saber cuántos octavos hay en 4, divide 4 por 1/8. Es decir,
Número de octavos en cuatro = 4 ÷\(\frac{1}{8}\).
Por otro lado, para encontrar el número de uno-ocho en cuatro, Figura demuestra\(\PageIndex{1}\) claramente que esto equivale a preguntar cuántas rebanadas de pizza hay en cuatro pizzas. Dado que hay 8 rebanadas por pizza y cuatro pizzas,
Número de rebanadas de pizza = 4 · 8.
La conclusión es el hecho de que 4 ÷ (1/8) equivale a 4 · 8. Es decir,
\[\begin{align*} 4 ÷ 1/8 &= 4 \cdot 8 \\[4pt] &= 32. \end{align*}\]
Por lo tanto, concluimos que hay 32 octavos en 4.
Reciprocales
El número 1 sigue siendo la identidad multiplicativa para las fracciones.
Propiedad de Identidad Multiplicativa
Deja que a/b sea cualquier fracción. Entonces,
\[ \frac{a}{b} \cdot 1 = \frac{a}{b} \text{ and } 1 \cdot \frac{a}{b} = \frac{a}{b}.\nonumber \]
El número 1 se llama la identidad multiplicativa porque el número idéntico se devuelve cuando se multiplica por 1.
A continuación, si invertimos 3/4, es decir, si volteamos 3/4 boca abajo, obtenemos 4/3. Tenga en cuenta lo que sucede cuando multiplicamos 3/4 por 4/3.
Al número 4/3 se le llama el inverso multiplicativo o recíproco de 3/4. El producto de los recíprocos es siempre 1.
Propiedad inversa multiplicativa
Deja que a/b sea cualquier fracción. El número b/a se llama el inverso multiplicativo o recíproco de a/b. El producto de los reciprocales es 1.
\[ \frac{a}{b} \cdot \frac{b}{a} = 1\nonumber \]
Nota: Para encontrar el inverso multiplicativo (recíproco) de un número, simplemente invierta el número (darle la vuelta).
Por ejemplo, el número 1/8 es el inverso multiplicativo (recíproco) de 8 porque
\[ 8 \cdot \frac{1}{8} = 1.\nonumber \]
Tenga en cuenta que 8 se puede considerar como 8/1. Invertir este número (darle la vuelta) para encontrar su multiplicativo inverso (recíproco) 1/8.
Ejemplo\(\PageIndex{1}\)
Encuentra las inversas multiplicativas (recíprocas) de: (a) 2/3, (b) −3/5, y (c) −12.
Solución
a) Porque
\[ \frac{2}{3} \cdot \frac{3}{2} = 1,\nonumber \]
el inverso multiplicativo (recíproco) de 2/3 es 3/2.
b) Porque
\[ - \frac{3}{5} \cdot \left( - \frac{5}{3} \right) = 1,\nonumber \]
el inverso multiplicativo (recíproco) de −3/5 es −5/3. Nuevamente, tenga en cuenta que simplemente invertimos el número −3/5 para obtener su recíproco −5/3.
c) Porque
\[ -12 \cdot \left( - \frac{1}{12} \right) = 1, \nonumber \]
el inverso multiplicativo (recíproco) de −12 es −1/12. Nuevamente, tenga en cuenta que simplemente invertimos el número −12 (entendido como igual a −12/1) para obtener su recíproco −1/12.
Ejercicio\(\PageIndex{1}\)
Encuentra los recíprocos de: (a) −3/7 y (b) 15
- Contestar
-
(a) −7/3, (b) 1/15
División
Recordemos que calculamos el número de una octava en cuatro haciendo este cálculo:
\[ \begin{align*} 4 ÷ \frac{1}{8} &= 4 · 8 \\[4pt] &= 32.\end{align*}\]
Observe cómo invertimos el divisor (segundo número), luego cambiamos la división a multiplicación. Esto motiva la siguiente definición de división.
Definición de División
Si a/b y c/d son fracciones, entonces
\[ \frac{a}{b} \div \frac{c}{d} = \frac{a}{b} \cdot \frac{d}{c}.\nonumber \]
Es decir, invertimos el divisor (segundo número) y cambiamos la división a multiplicación. Nota: Nos gusta usar la frase “invertir y multiplicar” como ayuda de memoria para esta definición.
Ejemplo\(\PageIndex{2}\)
Divide 1/2 por 3/5.
Solución
Para dividir 1/2 por 3/5, invierte el divisor (segundo número), luego multiplica.
\[ \begin{align*} \frac{1}{2} \div \frac{3}{5} &= \frac{1}{2} \cdot \frac{5}{3} ~ && \textcolor{red}{ \text{ Invert the divisor (second number).}} \\[4pt] &= \frac{5}{6} ~&& \textcolor{red}{ \text{ Multiply.}} \end{align*}\]
Ejercicio\(\PageIndex{2}\)
Dividir:
\[ \frac{2}{3} \div \frac{10}{3}\nonumber \]
- Contestar
-
1/5
Ejemplo\(\PageIndex{3}\)
Simplifica las siguientes expresiones: (a) 3 ÷\(\frac{2}{3}\) y (b)\(\frac{4}{5}\) ÷ 5.
Solución
En cada caso, invierte el divisor (segundo número), luego multiplica.
a) Obsérvese que 3 se entiende como 3/1.
\[ \begin{align*} 3 \div \frac{2}{3} &= \frac{3}{1} \cdot \frac{3}{2} ~ && \textcolor{red}{ \text{ Invert the divisor (second number).}} \\[4pt] &= \frac{9}{2} ~ && \textcolor{red}{ \text{ Multiply numerators; multiply denominators.}} \end{align*} \]
b) Obsérvese que 5 se entiende como 5/1.
\[ \begin{align*} \frac{4}{5} \div 5 &= \frac{4}{5} \cdot \frac{1}{5} ~ && \textcolor{red}{ \text{ Invert the divisor (second number).}} \\[4pt] &= \frac{4}{25} ~ && \textcolor{red}{ \text{ Multiply numerators; multiply denominators.}} \end{align*}\]
Ejercicio\(\PageIndex{3}\)
Dividir:
\[ \frac{15}{7} \div 5\nonumber \]
Contestar
-
\(\frac{3}{7}\)
Después de invertir, es posible que deba factorial y cancelar, como aprendimos a hacer en la Sección 4.2.
Ejemplo\(\PageIndex{4}\)
Divida −6/35 por 33/55.
Solución
Invertir, multiplicar, faccionar y cancelar factores comunes.
\[ \begin{aligned} - \frac{6}{35} \div \frac{33}{55} = - \frac{6}{35} \cdot \frac{55}{33} ~ & \textcolor{red}{ \text{ Invert the divisor (second number).}} \\ = - \frac{6 \cdot 55}{35 \cdot 33} ~ & \textcolor{red}{ \text{ Multiply numerators; multiply denominators.}} \\ = - \frac{(2 \cdot 3) \cdot (5 \cdot 11)}{(5 \cdot 7) \cdot (3 \cdot 11)} ~ & \textcolor{red}{ \text{ Factor numerators and denominators.}} \\ = - \frac{2 \cdot \cancel{3} \cdot \cancel{5} \cdot \cancel{11}}{ \cancel{5} \cdot 7 \cdot \cancel{3} \cdot \cancel{11}} ~ & \textcolor{red}{ \text{ Cancel common factors.}} \\ = - \frac{2}{7} ~ & \textcolor{red}{ \text{ Remaining factors.}} \end{aligned}\nonumber \]
Tenga en cuenta que a diferencia de los signos producen una respuesta negativa.
Ejercicio\(\PageIndex{4}\)
Dividir:
\[ \frac{6}{15} \div \left( - \frac{42}{35} \right)\nonumber \]
- Contestar
-
-1/3
Por supuesto, también puedes optar por facturar numeradores y denominadores en su lugar, luego cancelar factores comunes.
Ejemplo\(\PageIndex{5}\)
Dividir\(−6/x\) por\(−12/x^2\).
Solución
Invertir, faccionar numeradores y denominadores, cancelar factores comunes, luego multiplicar.
\[ \begin{align*} - \frac{6}{x} \div \left( - \frac{12}{x^2} \right) &= - \frac{6}{x} \cdot \left( - \frac{x^2}{12} \right) ~ && \textcolor{red}{ \text{ Invert second number.}} \\[4pt] &= - \frac{2 \cdot 3}{x} \cdot - \frac{x \cdot x}{2 \cdot 2 \cdot 3} ~ && \textcolor{red}{ \text{ Factor numerators and denominators.}} \\[4pt] &= - \frac{ \cancel{2} \cdot \cancel{3}}{ \cancel{x}} \cdot - \frac{ \cancel{x} \cdot x}{2 \cdot \cancel{2} \cdot \cancel{3}} ~ && \textcolor{red}{ \text{ Cancel common factors.}} \\[4pt] &= \frac{x}{2} ~ && \textcolor{red}{ \text{ Multiply.}} \end{align*}\]
Tenga en cuenta que los signos similares producen una respuesta positiva.
Ejercicio\(\PageIndex{5}\)
Dividir:
\[ - \frac{12}{a} \div \left( - \frac{15}{a^3} \right)\nonumber \]
- Contestar
-
\[ - \frac{4 a^2}{5}\nonumber \]
Ejercicios
En los Ejercicios 1-16, encuentra el recíproco del número dado.
1. −16/5
2. −3/20
3. −17
4. −16
5. 15/16
6. 7/9
7. 30
8. 28
9. −46
10. −50
11. −9/19
12. −4/7
13. 3/17
14. 3/5
15. 11
16. 48
En los Ejercicios 17-32, determinar qué propiedad de multiplicación es representada por la identidad dada.
17. \(\frac{2}{9} \cdot \frac{9}{2} = 1\)
18. \(\frac{12}{19} \cdot \frac{19}{12} = 1\)
19. \( \frac{−19}{12} \cdot 1 = \frac{−19}{12}\)
20. \(\frac{−19}{8} \cdot 1 = \frac{−19}{8}\)
21. \(−6 \cdot \left( − \frac{1}{6} \right) = 1\)
22. \(−19 \cdot \left( − \frac{1}{19} \right) = 1\)
23. \( \frac{−16}{11} \cdot 1 = \frac{−16}{11}\)
24. \(\frac{−7}{6} \cdot 1 = \frac{−7}{6}\)
25. \(− \frac{4}{1} \cdot \left( − \frac{1}{4} \right) = 1\)
26. \(− \frac{9}{10} \cdot \left( − \frac{10}{9} \right) = 1\)
27. \( \frac{8}{1} \cdot 1 = \frac{8}{1}\)
28. \(\frac{13}{15} \cdot 1 = \frac{13}{15}\)
29. \(14 \cdot \frac{1}{14} = 1\)
30. \(4 \cdot \frac{1}{4} = 1\)
31. \( \frac{13}{8} \cdot 1 = \frac{13}{8}\)
32. \(\frac{1}{13} \cdot 1 = \frac{1}{13}\)
En Ejercicios 33-56, divide las fracciones, y simplifica tu resultado.
33. \(\frac{8}{23} \div \frac{−6}{11}\)
34. \(\frac{−10}{21} \div \frac{−6}{5}\)
35. \(\frac{18}{19} \div \frac{−16}{23}\)
36. \(\frac{13}{10} \div \frac{17}{18}\)
37. \(\frac{4}{21} \div \frac{−6}{5}\)
38. \(\frac{2}{9} \div \frac{−12}{19}\)
39. \(\frac{−1}{9} \div \frac{8}{3}\)
40. \(\frac{1}{2} \div \frac{−15}{8}\)
41. \(\frac{−21}{11} \div \frac{3}{10}\)
42. \(\frac{7}{24} \div \frac{−23}{2}\)
43. \(\frac{−12}{7} \div \frac{2}{3}\)
44. \(\frac{−9}{16} \div \frac{6}{7}\)
45. \(\frac{2}{19} \div \frac{24}{23}\)
46. \(\frac{7}{3} \div \frac{−10}{21}\)
47. \(\frac{−9}{5} \div \frac{−24}{19}\)
48. \(\frac{14}{17} \div \frac{−22}{21}\)
49. \(\frac{18}{11} \div \frac{14}{9}\)
50. \(\frac{5}{6} \div \frac{20}{19}\)
51. \(\frac{13}{18} \div \frac{4}{9}\)
52. \(\frac{−3}{2} \div \frac{−7}{12}\)
53. \(\frac{11}{2} \div \frac{−21}{10}\)
54. \(\frac{−9}{2} \div \frac{−13}{22}\)
55. \(\frac{3}{10} \div \frac{12}{5}\)
56. \(\frac{−22}{7} \div \frac{−18}{17}\)
En Ejercicios 57-68, divide las fracciones, y simplifica tu resultado.
57. \(\frac{20}{17} \div 5\)
58. \(\frac{21}{8} \div 7\)
59. \(−7 \div \frac{21}{20}\)
60. \(−3 \div \frac{12}{17}\)
61. \(\frac{8}{21} \div 2\)
62. \(\frac{−3}{4} \div (−6)\)
63. \(8 \div \frac{−10}{17}\)
64. \(−6 \div \frac{20}{21}\)
65. \(−8 \div \frac{18}{5}\)
66. \(6 \div \frac{−21}{8}\)
67. \(\frac{3}{4} \div (−9)\)
68. \(\frac{2}{9} \div (−8)\)
En Ejercicios 69-80, divide las fracciones, y simplifica tu resultado.
69. \(\frac{11x^2}{12} \div \frac{8x^4}{3}\)
70. \(\frac{−4x^2}{3} \div \frac{11x^6}{6}\)
71. \(\frac{17y}{9} \div \frac{10y^6}{3}\)
72. \(\frac{−5y}{12} \div \frac{−3y^5}{2}\)
73. \(\frac{−22x^4}{13} \div \frac{12x}{11}\)
74. \(\frac{−9y^6}{4} \div \frac{24y^5}{13}\)
75. \(\frac{−3x^4}{10} \div \frac{−4x}{5}\)
76. \(\frac{18y^4}{11} \div \frac{4y^2}{7}\)
77. \(\frac{−15y^2}{14} \div \frac{−10y^5}{13}\)
78. \(\frac{3x}{20} \div \frac{2x^3}{5}\)
79. \(\frac{−15x^5}{13} \div \frac{20x^2}{19}\)
80. \(\frac{18y^6}{7} \div \frac{14y^4}{9}\)
En Ejercicios 81-96, divide las fracciones, y simplifica tu resultado.
81. \(\frac{11y^4}{14x^2} \div \frac{−9y^2}{7x^3}\)
82. \(\frac{−5x^2}{12y^3} \div \frac{−22x}{21y^5}\)
83. \(\frac{10x^4}{3y^4} \div \frac{7x^5}{24y^2}\)
84. \(\frac{20x^3}{11y^5} \div \frac{5x^5}{6y^3}\)
85. \(\frac{22y^4}{21x^5} \div \frac{−5y^2}{6x^4}\)
86. \(\frac{−7y^5}{8x^6} \div \frac{21y}{5x^5}\)
87. \(\frac{−22x^4}{21y^3} \div \frac{−17x^3}{3y^4}\)
88. \(\frac{−7y^4}{4x} \div \frac{−15y}{22x^4}\)
89. \(\frac{−16y^2}{3x^3} \div \frac{2y^6}{11x^5}\)
90. \(\frac{−20x}{21y^2} \div \frac{−22x^5}{y^6}\)
91. \(\frac{−x}{12y^4} \div \frac{−23x^3}{16y^3}\)
92. \(\frac{20x^2}{17y^3} \div \frac{8x^3}{15y}\)
93. \(\frac{y^2}{4x} \div \frac{−9y^5}{8x^3}\)
94. \(\frac{−10y^4}{13x^2} \div \frac{−5y^6}{6x^3}\)
95. \(\frac{−18x^6}{13y^4} \div \frac{3x}{y^2}\)
96. \(\frac{20x^4}{9y^6} \div \frac{14x^2}{17y^4}\)
RESPUESTAS
1. \(− \frac{5}{16}\)
3. \(− \frac{1}{17}\)
5. \(\frac{16}{15}\)
7. \(\frac{1}{30}\)
9. \(− \frac{1}{46}\)
11. \(− \frac{19}{9}\)
13. \(\frac{17}{3}\)
15. \(\frac{1}{11}\)
17. propiedad inversa multiplicativa
19. propiedad de identidad multiplicativa
21. propiedad inversa multiplicativa
23. propiedad de identidad multiplicativa
25. propiedad inversa multiplicativa
27. propiedad de identidad multiplicativa
29. propiedad inversa multiplicativa
31. identidad multiplicativa propiedad
33. \(− \frac{44}{69}\)
35. \(− \frac{207}{152}\)
37. \(− \frac{10}{63}\)
39. \(− \frac{1}{24}\)
41. \(− \frac{70}{11}\)
43. \(− \frac{18}{7}\)
45. \( \frac{23}{228}\)
47. \( \frac{57}{40}\)
49. \(\frac{81}{77}\)
51. \(\frac{13}{8}\)
53. \(− \frac{55}{21}\)
55. \(\frac{1}{8}\)
57. \(\frac{4}{17}\)
59. \(− \frac{20}{3}\)
61. \(\frac{4}{21}\)
63. \(− \frac{68}{5}\)
65. \(− \frac{20}{9}\)
67. \(− \frac{1}{12}\)
69. \(\frac{11}{32x^2}\)
71. \(\frac{17}{30y^5}\)
73. \(− \frac{121x^3}{78}\)
75. \(\frac{3x^3}{8}\)
77. \( \frac{39}{28y^3}\)
79. \(− \frac{57x^3}{52}\)
81. \(− \frac{11y^2x}{18}\)
83. \(\frac{80}{7xy^2}\)
85. \(− \frac{44y^2}{35x}\)
87. \(\frac{22xy}{119}\)
89. \(− \frac{88x^2}{3y^4}\)
91. \(\frac{4}{69x^2y}\)
93. \(− \frac{2x^2}{9y^3}\)
95. \(− \frac{6x^5}{13y^2}\)


