5.6: Fracciones y Decimales
- Page ID
- 113426
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Al convertir una fracción a decimal, solo puede suceder una de dos cosas. O el proceso terminará o la representación decimal comenzará a repetir un patrón de dígitos. En cada caso, el procedimiento para cambiar una fracción a un decimal es el mismo.
Cambio de una Fracción a Decimal
Para cambiar una fracción a decimal, divida el numerador por el denominador. Pista: Si primero reduce la fracción a términos más bajos, los números serán más pequeños y la división será un poco más fácil como resultado.
Terminación de decimales
Terminación de decimales
Primero reducir la fracción a los términos más bajos. Si el denominador de la fracción resultante tiene una factorización prima que consiste estrictamente en dos y/o cinco, entonces la representación decimal “terminará”.
Ejemplo 1
Cambiar 15/48 a un decimal.
Solución
Primero, reducir la fracción a los términos más bajos.
\[ \begin{aligned} \frac{15}{48} = \frac{3 \cdot 5}{3 \cdot 16} \\ = \frac{5}{16} \end{aligned}\nonumber \]
A continuación, tenga en cuenta que el denominador de 5/16 tiene factorización prima 16 = 2·2·2·2. Consiste sólo en dos. De ahí que la representación decimal de 5/16 deba terminar.
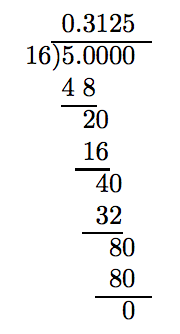
El resto cero termina el proceso. De ahí, 5/16 = 0.3125.
Ejercicio
Cambiar 10/16 a un decimal.
- Contestar
-
0.625
Ejemplo 2
Cambiar\(3 \frac{7}{20}\) a un decimal.
Solución
Tenga en cuenta que 7/20 se reduce a términos más bajos y su denominador tiene factorización de primos 20 = 2 · 2 · 5. Consiste sólo en dos y cinco. De ahí que la representación decimal de 7/20 deba terminar.
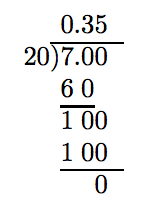
El resto cero termina el proceso. De ahí, 7/20 = 0.35. Por lo tanto,\(3 \frac{7}{20}\) = 3.35.
Ejercicio
Cambiar\(7 \frac{11}{20}\) a un decimal.
- Contestar
-
7.55
Decimales repetidos
Decimales repetidos
Primero reducir la fracción a los términos más bajos. Si la factorización prima del denominador resultante no consiste estrictamente en dos y cinco, entonces el proceso de división nunca tendrá un resto de cero. Sin embargo, los patrones repetidos de dígitos deben revelarse eventualmente.
Ejemplo 3
Cambiar 1/12 a un decimal.
Solución
Tenga en cuenta que 1/12 se reduce a términos más bajos y el denominador tiene una factorización prima 12 = 2 · 2 · 3 que no consiste estrictamente en dos y cinco. De ahí que la representación decimal de 1/12 no “terminará”. Tenemos que llevar a cabo la división hasta que reaparezca un resto por segunda ocasión. Esto indicará que la repetición está comenzando.
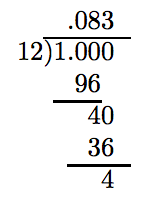
Obsérvese la segunda aparición de 4 como resto en la división anterior. Esto es un indicio de que la repetición está comenzando. No obstante, para estar seguros, llevemos a cabo la división por un par de lugares más.
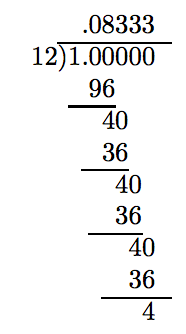
Observe cómo el resto 4 se repite una y otra vez. En el cociente, anote cómo el dígito 3 se repite una y otra vez. Es bastante evidente que si lleváramos a cabo la división unos cuantos lugares más, obtendríamos
\[\frac{1}{12} = 0.833333 \cdots\nonumber \]
La elipsis es una manera simbólica de decir que los tres se repetirán para siempre. Es el equivalente matemático de la palabra “etcétera”.
Ejercicio
Cambiar 5/12 a un decimal.
- Contestar
-
0.41666...
Hay una notación alternativa a los puntos suspensivos, a saber
\[ \frac{1}{12} = 0.08 \overline{3}.\nonumber \]
La barra sobre la 3 (llamada “barra repetitiva”) indica que la 3 se repetirá indefinidamente. Es decir,
\[0.08 \overline{3} = 0.083333 ....\nonumber \]
Uso de la barra de repetición
Para usar la notación de barras repetitivas, tome cualquier bloque de dígitos que esté debajo de la barra de repetición y duplique ese bloque de dígitos infinitamente a la derecha.
Así, por ejemplo:
- \(5. \overline{345} = 5.3454545 ....\)
- \(0. \overline{142857} = 0.142857142857142857 ....\)
Observación Importante
Aunque también\(0.8 \overline{33}\) producirá 0.8333333..., como regla debemos usar el menor número posible de dígitos debajo de la barra repetitiva. Por lo tanto,\(0.8 \overline{3}\) se prefiere sobre\(0.8 \overline{33}\).
Ejemplo 4
Cambiar 23/111 a decimal.
Solución
El denominador de 23/111 tiene factorización prima 111 = 3 ·37 y no consiste estrictamente en dos y cinco. De ahí que la representación decimal no “termine”. Tenemos que realizar la división hasta que detectemos un resto repetido.
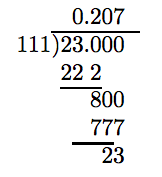
Anote el retorno de 23 como remanente. Así, el patrón de dígitos en el cociente debería comenzar de nuevo, pero agreguemos algunos lugares más a nuestra división para estar seguros.
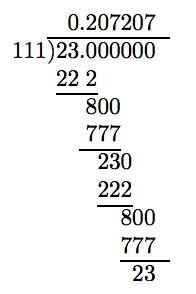
¡Ajá! Nuevamente un resto de 23. ¡Repetición! En este punto, confiamos en que
\[ \frac{23}{111} = 0.207207 ....\nonumber \]
Usando una “barra repetitiva”, se puede escribir este resultado
\[ \frac{23}{111} = 0. \overline{207}.\nonumber \]
Ejercicio
Cambiar 5/33 a un decimal.
- Contestar
-
0.151515...
Expresiones que contienen decimales y fracciones
En este punto podemos convertir fracciones a decimales, y viceversa, podemos convertir decimales en fracciones. Por lo tanto, deberíamos poder evaluar expresiones que contengan una mezcla de números de fracción y decimales.
Ejemplo 5
Simplificar:\(- \frac{3}{8} - 1.25\).
Solución
Cambiemos 1.25 a una fracción impropia.
\[ \begin{aligned} 1.25 = \frac{125}{100} ~ & \textcolor{red}{ \text{ Two decimal places } \Rightarrow \text{ two zeroes.} \\ = \frac{5}{4} ~ & \textcolor{red}{ \text{ Reduce to lowest terms.}} \end{aligned}\nonumber \]
En el problema original, sustituir 1.25 por 5/4, hacer fracciones equivalentes con un denominador común, luego restar.
\[ \begin{aligned} - \frac{3}{8} - 1.25 = - \frac{3}{8} - \frac{5}{4} ~ & \textcolor{red}{ \text{ Replace 1.25 with 5/4.}} \\ = - \frac{3}{8} - \frac{5 \cdot \textcolor{red}{2}}{4 \cdot \textcolor{red}{2}} ~ & \textcolor{red}{ \text{ Equivalent fractions, LCD = 8.}} \\ = - \frac{3}{8} - \frac{10}{8} ~ & \textcolor{red}{ \text{ Simplify the numerator and denominator.}} \\ = - \frac{3}{8} + \left( - \frac{10}{8} \right) ~ & \textcolor{red}{ \text{ Add the opposite.}} \\ = = \frac{13}{8} ~ & \textcolor{red}{ \text{ Add.}} \end{aligned}\nonumber \]
Así, −3/8 − 1.25 = −13/8.
Solución alternativa
Debido a que −3/8 se reduce a términos más bajos y 8 = 2 ·2 ·2 consiste solo en dos, la representación decimal de −3/8 terminará.
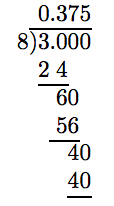
De ahí que −3/8 = −0.375. Ahora, reemplace −3/8 en el problema original por −0.375, luego simplifique.
\[ \begin{aligned} - \frac{3}{8} - 1.25 = -0.375 - 1.25 ~ & \textcolor{red}{ \text{ Replace } -3/8 \text{ with } -0.375.} \\ =-0.375 + (-1.25) ~ & \textcolor{red}{ \text{ Add the opposite.}} \\ = -1.625 ~ & \textcolor{red}{ \text{ Add.}} \end{aligned}\nonumber \]
Así, −3/8 − 1.25 = −1.625.
¿Son lo mismo?
El primer método produjo −13/8 como respuesta; el segundo método produjo −1.625. ¿Son estos los mismos resultados? Una forma de averiguarlo es cambiar −1.625 a una fracción impropia.
\[ \begin{aligned} -1.625 = - \frac{1625}{1000} ~ & \textcolor{red}{ \text{ Three places } \Rightarrow \text{ three zeroes.}} \\ = - \frac{5 \cdot 5 \cdot 5 \cdot 5 \cdot 13}{2 \cdot 2 \cdot 2 \cdot 5 \cdot 5 \cdot 5} ~ & \textcolor{red}{ \text{ Prime factor.}} \\ = - \frac{13}{2 \cdot 2 \cdot 2} ~ & \textcolor{red}{ \text{ Cancel common factors.}} \\ = - \frac{13}{8} ~ & \textcolor{red}{ \text{ Simplify.}} \end{aligned}\nonumber \]
Así, las dos respuestas son las mismas.
Ejercicio
Simplificar:\(− \frac{7}{8} − 6.5\)
- Contestar
-
\(−7 \frac{3}{8}\)o −7.375
Ejemplo 6
Simplificar:\(-\frac{2}{3} + 0.35\).
Solución
Atacemos esta expresión cambiando primero 0.35 a una fracción.
\[ \begin{aligned} - \frac{2}{3} + 0.35 = - \frac{2}{3} + \frac{35}{100} ~ & \textcolor{red}{ \text{ Change 0.35 to a fraction.}} \\ = - \frac{2}{3} + \frac{7}{20} ~ & \textcolor{red}{ \text{ Reduce 35/100 to lowest terms.}} \end{aligned}\nonumber \]
Encuentra una pantalla LCD, haz fracciones equivalentes y luego agrega.
\[ \begin{aligned} = - \frac{2 \cdot 20}{3 \cdot 20} + \frac{7 \cdot 3}{20 \cdot 3} ~ & \textcolor{red}{ \text{ Equivalent fractions with LCD = 60.}} \\ = - \frac{40}{60} + \frac{21}{60} ~ & \textcolor{red}{ \text{ Simplify numerators and denominators.}} \\ = - \frac{19}{60} ~ & \textcolor{red}{ \text{ Add.}} \end{aligned}\nonumber \]
Entonces,\(-\frac{2}{3} +0.35 = - \frac{19}{60}\).
Ejercicio
Simplificar:\(-\frac{4}{9} + 0.25\)
- Contestar
-
−7/36
En el Ejemplo 6, nos encontramos con problemas si tratamos de cambiar −2/3 a un decimal. La representación decimal para −2/3 es un decimal repetido (el denominador no se compone solo de dos y cinco). En efecto, −2/3 =\(−0. \overline{6}\). Para sumar\(−0. \overline{6}\) y 0.35, tenemos que alinear los puntos decimales, luego comenzar a sumar en el extremo derecho. ¡Pero no\(−0. \overline{6}\) tiene fin correcto! Esta observación lleva al siguiente consejo.
Observación Importante
Cuando se presenta un problema que contiene tanto decimales como fracciones, si la representación decimal de cualquier fracción se repite, lo mejor es cambiar primero todos los números a fracciones, luego simplificar.
Ejercicios
En Ejercicios 1-20, convierte la fracción dada a un decimal de terminación.
1. \(\frac{59}{16}\)
2. \(\frac{19}{5}\)
3. \(\frac{35}{4}\)
4. \(\frac{21}{4}\)
5. \(\frac{1}{16}\)
6. \(\frac{14}{5}\)
7. \(\frac{6}{8}\)
8. \(\frac{7}{175}\)
9. \(\frac{3}{2}\)
10. \(\frac{15}{16}\)
11. \(\frac{119}{175}\)
12. \(\frac{4}{8}\)
13. \(\frac{9}{8}\)
14. \(\frac{5}{2}\)
15. \(\frac{78}{240}\)
16. \(\frac{150}{96}\)
17. \(\frac{25}{10}\)
18. \(\frac{2}{4}\)
19. \(\frac{9}{24}\)
20. \(\frac{216}{150}\)
En los Ejercicios 21-44, convierta la fracción dada a un decimal repetido. Utilice la notación de “barra repetitiva”.
21. \(\frac{256}{180}\)
22. \(\frac{268}{180}\)
23. \(\frac{364}{12}\)
24. \(\frac{292}{36}\)
25. \(\frac{81}{110}\)
26. \(\frac{82}{99}\)
27. \(\frac{76}{15}\)
28. \(\frac{23}{9}\)
29. \(\frac{50}{99}\)
30. \(\frac{53}{99}\)
31. \(\frac{61}{15}\)
32. \(\frac{37}{18}\)
33. \(\frac{98}{66}\)
34. \(\frac{305}{330}\)
35. \(\frac{190}{495}\)
36. \(\frac{102}{396}\)
37. \(\frac{13}{15}\)
38. \(\frac{65}{36}\)
39. \(\frac{532}{21}\)
40. \(\frac{44}{60}\)
41. \(\frac{26}{198}\)
42. \(\frac{686}{231}\)
43. \(\frac{47}{66}\)
44. \(\frac{41}{198}\)
En los Ejercicios 45-52, simplifique la expresión dada convirtiendo primero la fracción en un decimal de terminación.
45. \(\frac{7}{4} − 7.4\)
46. \(\frac{3}{2} − 2.73\)
47. \(\frac{7}{5} + 5.31\)
48. \(− \frac{7}{4} + 3.3\)
49. \(\frac{9}{10} − 8.61\)
50. \(\frac{3}{4} + 3.7\)
51. \(\frac{6}{5} − 7.65\)
52. \(− \frac{3}{10} + 8.1\)
En los Ejercicios 53-60, simplifique la expresión dada convirtiendo primero el decimal en una fracción.
53. \(\frac{7}{6} − 2.9\)
54. \(− \frac{11}{6} + 1.12\)
55. \(− \frac{4}{3} − 0.32\)
56. \(\frac{11}{6} − 0.375\)
57. \(− \frac{2}{3} + 0.9\)
58. \(\frac{2}{3} − 0.1\)
59. \(\frac{4}{3} − 2.6\)
60. \(− \frac{5}{6} + 2.3\)
En los Ejercicios 61-64, simplificar la expresión dada.
61. \(\frac{5}{6} + 2.375\)
62. \(\frac{5}{3} + 0.55\)
63. \(\frac{11}{8} + 8.2\)
64. \(\frac{13}{8} + 8.4\)
65. \(− \frac{7}{10} + 1.2\)
66. \(− \frac{7}{5} − 3.34\)
67. \(− \frac{11}{6} + 0.375\)
68. \(\frac{5}{3} − 1.1\)
RESPUESTAS
1. 3.6875
3. 8.75
5. 0.0625
7. 0.75
9. 1.5
11. 0.68
13. 1.125
15. 0.325
17. 2.5
19. 0.375
21. \(1.4 \overline{2}\)
23. \(30. \overline{3}\)
25. \(0.7 \overline{36}\)
27. \(5.0 \overline{6}\)
29. \(0. \overline{50}\)
31. \(4.0 \overline{6}\)
33. \(1. \overline{48}\)
35. \(0. \overline{38}\)
37. \(0.8 \overline{6}\)
39. \(25. \overline{3}\)
41. \(0. \overline{13}\)
43. \(0.7 \overline{12}\)
45. −5.65
47. 6.71
49. −7.71
51. −6.45
53. \(− \frac{26}{15}\)
55. \(− \frac{124}{75}\)
57. \(\frac{7}{30}\)
59. \(− \frac{19}{15}\)
61. \(\frac{77}{24}\)
63. 9.575
65. 0.5
67. \(− \frac{35}{24}\)


