5.4: Multiplicar decimales

Última actualización
Guardar como PDF

Page ID: 113425

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Multiplicar números decimales implica dos pasos: (1) multiplicar los números como números enteros, ignorar el punto decimal y (2) colocar el punto decimal en la posición correcta en el producto o respuesta.

Por ejemplo, consideremos (0.7) (0.08), que nos pide encontrar el producto de “siete décimas” y “ocho centésimas”. Podríamos cambiar estos números decimales a fracciones, luego multiplicar.

\[ \begin{aligned} (0.7)(0.8) & = \frac{7}{10} \cdot \frac{8}{100} \\ & = \frac{56}{100} \\ & = 0.056 \end{aligned}\nonumber \]

El producto es 56/1000, o “cincuenta y seis milésimas”, que como decimal se escribe 0.056.

Observaciones Importantes

Hay dos observaciones muy importantes a realizar sobre el ejemplo (0.7) (0.08).

1. En forma fraccional

\[\frac{7}{10} \cdot \frac{8}{100} = \frac{56}{1000},\nonumber \]

tenga en cuenta que el numerador del producto se encuentra tomando el producto de los números enteros 7 y 8. Es decir, ignoras los decimales en 0.7 y 0.08 y multiplicas 7 y 8 como si fueran números enteros.

2. El primer factor, 0.7, tiene un dígito a la derecha del punto decimal. Su equivalente fraccional, 7/10, tiene un cero en su denominador. El segundo factor, 0.08, tiene dos dígitos a la derecha del punto decimal. Su equivalente fraccional, 8/100, tiene dos ceros en su denominador. Por lo tanto, el producto 56/1000 se ve obligado a tener tres ceros en su denominador y su equivalente decimal, 0.056, debe por lo tanto tener tres dígitos a la derecha del punto decimal.

Veamos otro ejemplo.

Ejemplo 1

Simplificar: (2.34) (1.2).

Solución

Cambiar los números decimales “dos y treinta y cuatro centésimas” y “una y dos décimas” a fracciones, luego multiplica.

\[ \begin{aligned} (2.34)(1.2) = 2 \frac{34}{100} \cdot 1 \frac{2}{10} ~ & \textcolor{red}{ \text{ Change decimals to fractions.}} \\ = \frac{234}{100 \cdot \frac{12}{10} ~ & \textcolor{red}{ \text{ Change mixed to improper fractions.}} \\ = \frac{2808}{1000} ~ & \textcolor{red}{ \text{ Multiply numerators and denominators.}} \\ = 2 \frac{808}{1000} ~ & \textcolor{red}{ \text{ Change to mixed fraction.}} \\ = 2.808 ~ & \textcolor{red}{ \text{ Change back to decimal form.}} \end{aligned}\nonumber \]

Ejercicio

Multiplicar: (1.86) (9.5)

Contestar: 17.67

Observaciones Importantes

Hacemos las mismas dos observaciones que en el ejemplo anterior.

Si tratamos los números decimales como números enteros sin decimales, entonces (234) (12) = 2808, que es el numerador de la fracción 2808/1000 en la solución que se muestra en el Ejemplo 1. Estos son también los mismos dígitos que se muestran en la respuesta 2.808.
Hay dos dígitos a la derecha del punto decimal en el primer factor 2.34 y un dígito a la derecha del punto decimal en el segundo factor 1.2. Se trata de un total de tres dígitos a la derecha de los puntos decimales en los factores, que es precisamente el mismo número de dígitos que aparecen a la derecha del punto decimal en la respuesta 2.808.

Las observaciones hechas al final de los dos ejemplos anteriores nos llevan al siguiente método.

Multiplicar números decimales

Para multiplicar dos números decimales, realice los siguientes pasos:

Ignorar los puntos decimales en los factores y multiplicar los dos factores como si fueran números enteros.
Contar el número de dígitos a la derecha del punto decimal en cada factor. Suma estos dos números.
Coloque el punto decimal en el producto para que el número de dígitos a la derecha del punto decimal sea igual a la suma que se encuentra en el paso 2.

Ejemplo 2

Siga los pasos descritos en Multiplicar números decimales para encontrar el producto en el Ejemplo 1.

Solución

Seguimos los pasos descritos en Multiplicar números decimales.

1. El primer paso es multiplicar los factores 2.34 y 1.2 como números enteros, ignorando los puntos decimales.

\[ \begin{array}{r} 234 \\ \times 12 \\ \hline 468 \\ 234 \\ \hline 2808 \end{array}\nonumber \]

2. El segundo paso es encontrar la suma del número de dígitos a la derecha de los puntos decimales en cada factor. Tenga en cuenta que 2.34 tiene dos dígitos a la derecha del punto decimal, mientras que 1.2 tiene un dígito a la derecha del punto decimal. Así, tenemos un total de tres dígitos a la derecha de los puntos decimales en los factores.

3. El tercer y último paso es colocar el punto decimal en el producto o respuesta para que haya un total de tres dígitos a la derecha del punto decimal. Por lo tanto,

(2.34) (1.2) = 2.808.

Tenga en cuenta que esta es precisamente la misma solución que se encuentra en el Ejemplo 1.

Lo que sigue es una manera conveniente de organizar tu trabajo en formato vertical.

\[ \begin{array}{r} 2.34 \\ \times 1.2 \\ \hline 468 \\ 2 ~ 34 \\ \hline 2.808 \end{array}\nonumber \]

Ejercicio

Multiplicar: (5.98) (3.7)

Contestar: 22.126

Ejemplo 3

Simplificar: (8.235) (2.3).

Solución

Utilizamos el conveniente formato vertical introducido al final del Ejemplo 2.

\[ \begin{array}{r} 8.235 \\ \times 2.3 \\ \hline 2~4705 \\ 16 ~ 470 \\ \hline 18.9405 \end{array}\nonumber \]

El factor 8.235 tiene tres dígitos a la derecha del punto decimal; el factor 2.3 tiene un dígito a la derecha del punto decimal. Por lo tanto, debe haber un total de cuatro dígitos a la derecha del punto decimal en el producto o respuesta.

Ejercicio

Multiplicar: (9.582) (8.6)

Contestar: 82.4052

Multiplicar números decimales firmados

Las reglas que rigen la multiplicación de números decimales firmados son idénticas a las reglas que rigen la multiplicación de enteros.

Como Signos. El producto de dos números decimales con signos similares es positivo. Es decir:

(+) (+) = + y (−) (−) = +

A diferencia de Signos. El producto de dos números decimales con signos diferentes es negativo. Es decir:

(+) (−) = − y (−) (+) = −

Ejemplo 4

Simplificar: (−2.22) (−1.23).

Solución

Ignorar las señales para hacer la multiplicación, luego considerar las señales en la respuesta final detrás.

Como cada factor tiene dos dígitos a la derecha del punto decimal, debe haber un total de 4 decimales a la derecha del punto decimal en el producto.

\[ \begin{array}{r} 2.22 \\ \times 1.23 \\ \hline \\ 666 \\ 444 \\ 1~11 \\ \hline 1.6206 \end{array}\nonumber \]

Los signos similares dan un producto positivo. Por lo tanto:

(−2.22) (−1.23) = 1.6206

Ejercicio

Multiplicar: (−3.86) (−5.77)

Contestar: 22.2722

Ejemplo 5

Simplificar: (5.68) (−0.012).

Solución

Ignora las señales para hacer la multiplicación, luego considere las señales en la respuesta final a continuación.

El primer factor tiene dos dígitos a la derecha del punto decimal, el segundo factor tiene tres. Por lo tanto, debe haber un total de cinco dígitos a la derecha del punto decimal en el producto o respuesta. Esto requiere anteponer un cero extra frente a nuestro producto.

\[ \begin{array}{r} 5.68 \\ \times 0.012 \\ \hline 1136 \\ 568 \\ \hline 0.06816 \end{array}\nonumber \]

A diferencia de los signos dan un producto negativo. Por lo tanto:

(5.68) (−0.012) = −0.06816

Ejercicio

Multiplicar: (9.23) (−0.018)

Contestar: −0.16614

Orden de Operaciones

También se aplican a los números decimales las mismas Reglas Guía Orden de Operaciones.

Reglas que guían el orden de operaciones

Al evaluar expresiones, proceda en el siguiente orden.

Evalúe primero las expresiones contenidas en los símbolos de agrupación. Si los símbolos de agrupación están anidados, evalúe primero la expresión en el par más interno de símbolos de agrupación.
Evaluar todos los exponentes que aparecen en la expresión.
Realizar todas las multiplicaciones y divisiones en el orden en que aparezcan en la expresión, moviéndose de izquierda a derecha.
Realizar todas las sumas y restaciones en el orden en que aparezcan en la expresión, moviéndose de izquierda a derecha.

Ejemplo 6

Si a = 3.1 y b = −2.4, evalúe a ² − 3.2 b ²

Solución

Preparar la expresión para sustitución usando paréntesis.

\[a^2 − 3.2b^2 = (~)^2 − 3.2(~)^2\nonumber \]

Sustituir 3.1 por a y −2.4 por b y simplificar.

\[ \begin{aligned} a^2 - 3.2b^2 = (3.1)^2 -3.2(-2.4)^2 ~ & \textcolor{red}{ \text{ Substitute: 3.1 for } a, ~ -2.4 \text{ for } b.} \\ =9.61 - 3.2(5.76) ~ & \textcolor{red}{ \text{ Exponents first: } (3.1)^2 = 9.61,~ (-2.4)^2 = 5.76} \\ =9.61 - 18.432 ~ & \textcolor{red}{ \text{ Multiply: } 3.2(5.76)=18.432} \\ = -8.822 ~ & \textcolor{red}{ \text{ Subtract: } 9.61 - 18.432 = -8.822} \end{aligned}\nonumber \]

Ejercicio

Si a = 3.8 y b = −4.6, evalúe la expresión: 2.5 a ² − b ²

Contestar: 14.94

Poderes de Diez

Considerar:

\[ \begin{array}{l}10^1 = 10 \\ 10^2 = 10 \cdot 10 = 100 \\ 10^3 = 10 \cdot 10 \cdot 10 = 1,000 \\ 10^4 = 10 \cdot 10 \cdot 10 \cdot 10 = 10,000 \end{array}\nonumber \]

¡Anote la respuesta para 10 ⁴, un uno seguido de cuatro ceros! ¿Ves el patrón?

Poderes de Diez

En la expresión 10 ⁿ, el exponente coincide con el número de ceros en la respuesta. De ahí que 10 ⁿ será un 1 seguido de n ceros.

Ejemplo 7

Simplificar: 10 ⁹.

Solución

10 ⁹ debe ser un 1 seguido de 9 ceros. Es decir,

\[10^9 = 1, 000, 000, 000,\nonumber \]

o “mil millones”.

Ejercicio

Simplificar: 10 ⁶

Contestar: 1,000,000

Multiplicar números decimales por potencias de diez

Multipliquemos 1.234567 por 10 ³, o equivalentemente, por 1,000. Ignorar el punto decimal y multiplicar los números como números enteros.

\[ \begin{array}{r} 1.234567 \\ \times 1000 \\ \hline 1234.567000 \end{array}\nonumber \]

La suma total de dígitos a la derecha del punto decimal en cada factor es 6. Por lo tanto, colocamos el punto decimal en el producto para que haya seis dígitos a la derecha del punto decimal.

Sin embargo, los ceros finales pueden eliminarse sin cambiar el valor del producto. Es decir, 1.234567 veces 1000 es 1234.567. Tenga en cuenta que el punto decimal en el producto está tres lugares más a la derecha que en el factor original. Esta observación lleva al siguiente resultado.

Multiplicar un número decimal por una potencia de diez

Multiplicar un número decimal por 10 ⁿ moverá el punto decimal n lugares hacia la derecha.

Ejemplo 8

Simplificar: 1.234567 · 10 ⁴

Solución

Multiplicando por 104 (o equivalentemente, por 10,000) mueve los decimales 4 lugares a la derecha. Así, 1.234567 · 10, 000 = 12345.67.

Ejercicio

Simplificar: 1.234567 · 10 ²

Contestar: 123.4567

El Círculo

Empecemos con una definición.

El Círculo

Un círculo es la colección de todos los puntos equidistantes de un punto O dado, llamado el centro del círculo.

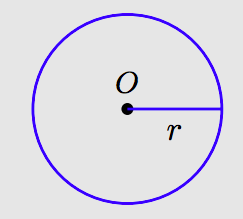
$Screen Shot 2019-09-11 a las 12.14.28 PM.png$

El segmento que une cualquier punto del círculo al centro del círculo se denomina radio del círculo. En la figura anterior, la variable r representa la longitud del radio del círculo

Necesitamos otro término, el diámetro de un círculo.

El diámetro de un círculo

Si dos puntos en un círculo están conectados con un segmento de línea, entonces ese segmento se llama cuerda del círculo. Si el acorde pasa por el centro del círculo, entonces el acorde se llama el diámetro del círculo.

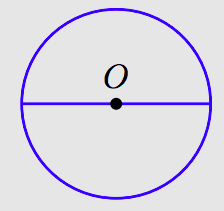
$Screen Shot 2019-09-11 a las 12.18.01 PM.png$

En la figura anterior, la variable d representa la longitud del diámetro del círculo. Tenga en cuenta que el diámetro es el doble de la longitud del radio; en símbolos

\[d=2r.\nonumber \]

La circunferencia de un círculo

Cuando trabajamos con polígonos, el perímetro del polígono se encuentra sumando las longitudes de sus bordes. El círculo usa un nombre diferente para su perímetro.

La circunferencia de un círculo

La longitud del círculo se llama su circunferencia. Usualmente usamos la variable C para denotar la circunferencia de un círculo

Es decir, si uno caminara por el círculo, la distancia total recorrida en una revolución es la circunferencia del círculo.

Los antiguos matemáticos de Egipto y Grecia notaron una relación llamativa entre la circunferencia de un círculo y su diámetro. Descubrieron que cada vez que divides la circunferencia de un círculo por su diámetro, obtienes una constante. Es decir, si tomas un círculo muy grande y divides su circunferencia por su diámetro, obtienes exactamente el mismo número si tomas un círculo muy pequeño y divides su circunferencia por su diámetro. Esta constante común se denominó π (“pi”).

Relacionar la Circunferencia y el Diámetro

Siempre que la circunferencia de un círculo se divide por su diámetro, la respuesta es la constante π. Es decir, si C es la circunferencia del círculo y d es el diámetro del círculo, entonces

\[\frac{C}{d} = \pi.\nonumber \]

En los tiempos modernos, solemos multiplicar ambos lados de esta ecuación por d para obtener la fórmula para la circunferencia de un círculo.

\[C = \pi d\nonumber \]

Debido a que el diámetro de un círculo es el doble de la longitud de su radio, podemos sustituir d = 2 r en la última ecuación para obtener una forma alternativa de la ecuación de circunferencia.

\[C = \pi (2r) = 2 \pi r\nonumber \]

El número π tiene una historia rica e histórica. Geometros antiguos de Egipto, Babilonia, India y Grecia sabían que π era un poco más grande que 3. Las primeras aproximaciones conocidas datan alrededor del 1900 a.C. (Wikipedia); son 25/8 (Babilonia) y 256/81 (Egipto). El texto indio Shatapatha Brahmana da π como 339/108 ≈ 3.139. Arquímedes (287-212 a.C.) fue el primero en estimar π rigurosamente, aproximando la circunferencia de un círculo con polígonos inscritos y circunscritos. Pudo probar que 223/71 < π < 22/7. Tomando el promedio de estos valores arroja π ≈ 3.1419. Los matemáticos modernos han demostrado que π es un número irracional, un decimal infinito que nunca repite ningún patrón. Los matemáticos, con la ayuda de computadoras, producen rutinariamente aproximaciones de π con miles de millones de dígitos después del punto decimal.

Dígitos de Pi

Aquí está π, correcto a los primeros cincuenta dígitos.

π = 3.14159265358979323846264338327950288419716939937510...

El número de dígitos de π utilizados depende de la aplicación. Trabajando a escalas muy pequeñas, uno podría mantener muchos dígitos de π, pero si está construyendo una cerca circular de jardín en su patio trasero, entonces se necesitan menos dígitos de π.

Ejemplo 9

Encuentra la circunferencia de un círculo dado que su radio es de 12 pies.

Solución

La circunferencia del círculo viene dada por la fórmula C = π d, o, porque d = 2 r,

\[C = 2πr.\nonumber \]

Sustituto 12 por r.

\[C = 2πr = 2π(12) = 24π\nonumber \]

Por lo tanto, la circunferencia del círculo es exactamente C = 24π pies.

Podemos aproximar la circunferencia ingresando una aproximación para π. Usemos π ≈ 3.14. Nota: El símbolo ≈ se lee “aproximadamente igual a”.

\[C = 24π ≈ 24(3.14) ≈ 75.36 \text{ feet}\nonumber \]

Es importante entender que la solución C = 24π pies es la circunferencia exacta, mientras que C ≈ 75.36 pies es solo una aproximación.

Ejercicio

Encuentra el radio de un círculo que tiene un radio de 14 pulgadas. Usar π ≈ 3.14

Contestar: 87.92 pulgadas

El área de un círculo

Aquí hay un argumento razonable utilizado para ayudar a desarrollar una fórmula para el área de un círculo. Comience con un círculo de radio r y divídalo en 8 cuñas iguales, como se muestra en la figura que sigue.

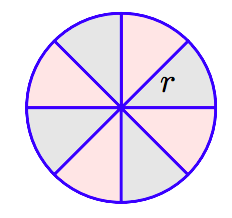
$Screen Shot 2019-09-11 a las 12.31.33 PM.png$

Reorganice las piezas como se muestra en la siguiente figura.

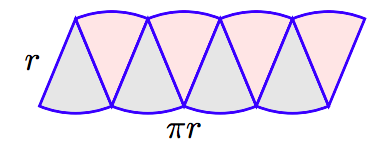
$Screen Shot 2019-09-11 a las 12.31.39 PM.png$

Tenga en cuenta que las piezas reordenadas casi forman un rectángulo con longitud aproximadamente la mitad de la circunferencia del círculo, π r, y ancho aproximadamente r. El área sería aproximadamente A ≈ (largo) (ancho) ≈ (π r) (r) ≈ π r ². Esta aproximación sería aún mejor si duplicamos el número de cuñas del círculo.

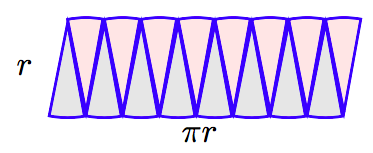
$Screen Shot 2019-09-11 a las 12.31.43 PM.png$

Si volviéramos a duplicar el número de cuñas, la cifra resultante se parecería aún más a un rectángulo con longitud πr y ancho r, lo que lleva a la siguiente conclusión.

El área de un círculo

El área de un círculo de radio r viene dada por la fórmula

\[A = \pi r^2.\nonumber \]

Ejemplo 10

Encuentra el área de un círculo que tiene un diámetro de 12.5 metros. Usa 3.14 para π y redondea la respuesta para el área a la décima de metro cuadrado más cercana.

Solución

El diámetro es el doble del radio.

\[d = 2r\nonumber \]

Sustituir 12.5 por d y resolver por r.

\[ \begin{aligned} 12.5 = 2r ~ & \textcolor{red}{ \text{ Substitute 12.5 for } d.} \\ \frac{12.5}{2} = \frac{2r}{2} ~ & \textcolor{red}{ \text{ Divide both sides by 2.}} \\ 6.25 = r ~ & \textcolor{red}{ \text{ Simplify.}} \end{aligned}\nonumber \]

De ahí que el radio sea de 6.25 metros. Para encontrar el área, usa la fórmula

\[A = \pi r^2\nonumber \]

y sustituto: 3.14 para π y 6.25 para r.

\[ \begin{aligned} A = (3.14)(6.25)^2 ~ & \textcolor{red}{ \text{ Substitute: 3.14 for } \pi, \text{ 6.25 for } r.} \\ = (3.14)(39.0625) ~ & \textcolor{red}{ \text{ Square first: } (6.25)^2 = 39.0625} \\ =122.65625 ~ & \textcolor{red}{ \text{ Multiply: } (3.14)(39.0625) = 122.65625} \end{aligned}\nonumber \]

De ahí que el área aproximada del círculo sea A = 122.65625 metros cuadrados. Para redondear al décimo de metro cuadrado más cercano, identifique el dígito de redondeo y el dígito de prueba.

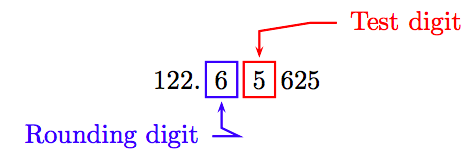
$Screen Shot 2019-09-11 a las 12.36.46 PM.png$

Debido a que el dígito de prueba es mayor o igual a 5, agregue 1 al dígito de redondeo y trunca. Así, correcto a la décima de metro cuadrado más cercana, el área del círculo es aproximadamente

\[A ≈ 122.7 \text{ m}^2.\nonumber \]

Ejercicio

Encuentra el área de un círculo que tiene un radio de 12.2 centímetros. Usar π ≈ 3.14

Contestar: 467.3576 cm ²

Ejercicios

En los Ejercicios 1-28, multiplica los decimales.

1. (6.7) (0.03)

2. (2.4) (0.2)

3. (28.9) (5.9)

4. (33.5) (2.1)

5. (4.1) (4.6)

6. (2.6) (8.2)

7. (75.3) (0.4)

8. (21.4) (0.6)

9. (6.98) (0.9)

10. (2.11) (0.04)

11. (57.9) (3.29)

12. (3.58) (16.3)

13. (47.3) (0.9)

14. (30.7) (0.4)

15. (9.9) (6.7)

16. (7.2) (6.1)

17. (19.5) (7.9)

18. (43.4) (8.9)

19. (6.9) (0.3)

20. (7.7) (0.7)

21. (35.3) (3.81)

22. (5.44) (9.58)

23. (2.32) (0.03)

24. (4.48) (0.08)

25. (3.02) (6.7)

26. (1.26) (9.4)

27. (4.98) (6.2)

28. (3.53) (2.9)

En los Ejercicios 29-56, multiplica los decimales.

29. (−9.41) (0.07)

30. (4.45) (−0.4)

31. (−7.4) (−0.9)

32. (−6.9) (0.05)

33. (−8.2) (3.7)

34. (−7.5) (−6.6)

35. (9.72) (−9.1)

36. (6.22) (−9.4)

37. (−6.4) (2.6)

38. (2.3) (−4.4)

39. (−39.3) (−0.8)

40. (57.7) (−0.04)

41. (63.1) (−0.02)

42. (−51.1) (−0.8)

43. (−90.8) (3.1)

44. (−74.7) (2.9)

45. (47.5) (−82.1)

46. (−14.8) (−12.7)

47. (−31.1) (−4.8)

48. (−28.7) (−6.8)

49. (−2.5) (−0.07)

50. (−1.3) (−0.05)

51. (1.02) (−0.2)

52. (−7.48) (−0.1)

53. (7.81) (−5.5)

54. (−1.94) (4.2)

55. (−2.09) (37.9)

56. (20.6) (−15.2)

En los Ejercicios 57-68, multiplique el decimal por la potencia dada de 10.

57. 24.264 · 10

58. 65.722 · 100

59. 53.867 · 10 ⁴

60. 23.216 · 10 ⁴

61. 5.096 · 10 ³

62. 60.890 · 10 ³

63. 37.968 · 10 ³

64. 43.552 · 10 ³

65. 61.303 · 100

66. 83.837 · 1000

67. 74.896 · 1000

68. 30.728 · 100

En los Ejercicios 69-80, simplificar la expresión dada.

69. (0.36) (7.4) − (−2.8) ²

70. (−8.88) (−9.2) − (−2.3) ²

71. 9.4 − (−7.7) (1.2) ²

72. 0.7 − (−8.7) (−9.4) ²

73. 5.94 − (−1.2) (−1.8) ²

74. −2.6 − (−9.8) (9.9) ²

75. 6.3 − 4.2 (9.3) ²

76. 9.9 − (−4.1) (8.5) ²

77. (6.3) (1.88) − (−2.2) ²

78. (−4.98) (−1.7) − 3.52

79. (−8.1) (9.4) − 1.8 ²

80. (−3.63) (5.2) − 0.8 ²

81. Dado a = −6.24, b = 0.4, y c = 7.2, evaluar la expresión a − bc ².

82. Dado a = 4.1, b = −1.8 y c = −9.5, evaluar la expresión a − bc ².

83. Dado a = −2.4, b = −2.1 y c = −4.6, evalúe la expresión ab − c ².

84. Dado a = 3.3, b = 7.3, y c = 3.4, evaluar la expresión ab − c ².

85. Dado a = −3.21, b = 3.5 y c = 8.3, evaluar la expresión a − bc ².

86. Dado a = 7.45, b = −6.1 y c = −3.5, evaluar la expresión a − bc ².

87. Dado a = −4.5, b = −6.9 y c = 4.6, evaluar la expresión ab − c ².

88. Dado a = −8.3, b = 8.2 y c = 5.4, evaluar la expresión ab − c ².

89. Un círculo tiene un diámetro de 8.56 pulgadas. Usando π ≈ 3.14, encuentra la circunferencia del círculo, correcta a la décima de pulgada más cercana.

90. Un círculo tiene un diámetro de 14.23 pulgadas. Usando π ≈ 3.14, encuentra la circunferencia del círculo, correcta a la décima de pulgada más cercana.

91. Un círculo tiene un diámetro de 12.04 pulgadas. Usando π ≈ 3.14, encuentra la circunferencia del círculo, correcta a la décima de pulgada más cercana.

92. Un círculo tiene un diámetro de 14.11 pulgadas. Usando π ≈ 3.14, encuentra la circunferencia del círculo, correcta a la décima de pulgada más cercana.

93. Un círculo tiene un diámetro de 10.75 pulgadas. Usando π ≈ 3.14, encuentra el área del círculo, correcta a la centésima de pulgada cuadrada más cercana.

94. Un círculo tiene un diámetro de 15.49 pulgadas. Usando π ≈ 3.14, encuentra el área del círculo, correcta a la centésima de pulgada cuadrada más cercana.

95. Un círculo tiene un diámetro de 13.96 pulgadas. Usando π ≈ 3.14, encuentra el área del círculo, correcta a la centésima de pulgada cuadrada más cercana.

96. Un círculo tiene un diámetro de 15.95 pulgadas. Usando π ≈ 3.14, encuentra el área del círculo, correcta a la centésima de pulgada cuadrada más cercana.

97. Sue ha decidido construir un estanque circular para peces cerca de su patio. Ella quiere que tenga 15 pies de diámetro y 1.5 pies de profundidad. ¿Cuál es el volumen de agua que va a contener? Usar π ≈ 3.14. Pista: El volumen de un cilindro viene dado por la fórmula V = πr ² h, que es el área de la base circular multiplicada por la altura del cilindro.

98. John tiene que tomar una decisión con respecto a su empleo. Actualmente tiene trabajo en Taco Loco en Fortuna. Después de impuestos, gana alrededor de $9.20 por hora y trabaja alrededor de 168 horas al mes. Actualmente paga $400 mensuales por renta. Tiene la oportunidad de mudarse a Santa Rosa y tomar un trabajo en Mi Ultimo Refugio que pagaría 10.30 dólares por hora después de impuestos por 168 horas al mes, pero su renta costaría 570 dólares mensuales.

a) Después de pagar la vivienda en Fortuna, ¿cuánto le queda cada mes para otros gastos?

b) Después de pagar la vivienda en Santa Rosa, ¿cuánto le habría sobrado cada mes para otros gastos?

c) ¿Para qué trabajo le quedaría más dinero después de pagar la renta y cuánto sería?

99. John decidió mudarse a Santa Rosa y tomar el trabajo en Mi Ultimo Refugio (ver Ejercicio 98). Pudo incrementar sus ingresos porque podía trabajar 4 domingos al mes a tiempo y medio. Por lo que ahora trabajaba 32 horas al mes a tiempo y medio y 136 horas a la tasa regular de 10.30 dólares (todo después de que se retiraran los impuestos). Nota: Anteriormente había trabajado 168 horas mensuales a $10.30 por hora.

a) ¿Cuál era su nuevo ingreso mensual?

b) ¿Cuánto aumentaron sus ingresos mensuales?

100. Factura eléctrica. En una factura reciente, PGE cobró 0.11531 dólares por Kwh por los primeros 333 Kwh de energía eléctrica utilizada. Si un hogar usaba 312 Kwh de energía, ¿cuál era su factura eléctrica?

101. Cabernet. En el Valle de Napa, un acre de buena tierra puede producir alrededor de 3.5 toneladas de uvas de calidad. A un precio promedio de $3,414 por tonelada para cabernet premium, ¿cuánto dinero podrías generar en un acre de cultivo de cabernet? Associated Press-Times-Standard 03/11/10 La polilla de la uva amenaza el método de cultivo del Valle de

102. Fertilizante. Usando las tarifas personalizadas de Ohio Farm 2008, el costo promedio para esparcir fertilizantes secos a granel es de aproximadamente $4.50 por acre. ¿Cuál es el costo de fertilizar 50 acres?

103. Agronegocios. Enormes agrograneros corporativos albergan a 1000 cerdos cada uno.

a) Si cada cerdo pesa aproximadamente 100 libras, ¿cuántas libras de cerdo hay en cada almacén?

b) A un promedio de $1.29 por libra, ¿cuál es el valor total en efectivo de una agribarn corporativa? Associated Press-Times-Standard 12/29/09 Aumenta la presión para detener los antibióticos en la agricultura.

104. Naufragios. Una docena de naufragios centenarios fueron encontrados en el Mar Báltico por una compañía de gas que construía un oleoducto submarino entre Rusia y Alemania. Los 12 naufragios fueron encontrados en un corredor de 30 millas de largo y 1.2 millas de ancho a una profundidad de 430 pies. Modelar el corredor con un rectángulo y encontrar el área aproximada de la región donde se encontraron las naves. Associated Press-Times-Standard 03/10/10 Naufragios centenarios encontrados en el Mar Báltico.

105. Plato de radio. El diámetro de la “flota de caballos de batalla” de los radiotelescopios, como el de Goldstone, California, es de 230 pies. ¿Cuál es la circunferencia de la antena parabólica del radiotelescopio al décimo más cercano? Associated Press-Times-Standard 03/09/2010 La NASA reparará la antena del espacio profundo en el desierto de California.

RESPUESTAS

1. 0.201

3. 170.51

5. 18.86

7. 30.12

9. 6.282

11. 190.491

13. 42.57

15. 66.33

17. 154.05

19. 2.07

21. 134.493

23. 0.0696

25. 20.234

27. 30.876

29. −0.6587

31. 6.66

33. −30.34

35. −88.452

37. −16.64

39. 31.44

41. −1.262

43. −281.48

45. −3899.75

47. 149.28

49. 0.175

51. −0.204

53. −42.955

55. −79.211

57. 242.64

59. 538670

61. 5096

63. 37968

65. 6130.3

67. 74896

69. −5.176

71. 20.488

73. 9.828

75. −356.958

77. 7.004

79. −79.38

81. −26.976

83. −16.12

85. −244.325

87. 9.89

89. 26.9 pulg.

91. 37.8 pulg.

93. 90.72 pulgadas cuadradas

95. 152.98 pulgadas cuadradas

97. 264.9375 pies cúbicos

99.

a) $1895.20

b) 164.80$

101. $11.949

103.

a) 100, 000 libras

b) 129,000 dólares

105. 722.2 pies

Search

Text Color

Text Size

Margin Size

Font Type