5.7: Ecuaciones con decimales

Última actualización
Guardar como PDF

Page ID: 113428

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Podemos sumar o restar el mismo número decimal de ambos lados de una ecuación sin afectar la solución.

Ejemplo 1

Resolver para x: x − 1.35 = −2.6.

Solución

Para deshacer restando 1.35, suma 1.35 a ambos lados de la ecuación.

\[ \begin{aligned} x - 1.35 = -2.6 ~ & \textcolor{red}{ \text{ Original equation.}} \\ x - 1.35 + 1.35 = -2.6 + 1.35 ~ & \textcolor{red}{ \text{ Add 1.35 to both sides.}} \\ x = -1.25 ~ & \textcolor{red}{ \text{ Simplify: } -2.6 + 1.35 = -1.25.} \end{aligned}\nonumber \]

Ejercicio

Resolver para x:$x+1.25=0.6$

Contestar: −0.65

Todavía podemos multiplicar ambos lados de una ecuación por el mismo número decimal sin afectar la solución.

Ejemplo 2

Resolver para x:$\frac{x}{-0.35} = 4.2$.

Solución

Para deshacer dividiendo por −0.35, multiplica ambos lados de la ecuación por −0.35.

\[ \begin{aligned} \frac{x}{-0.35} = 4.2 ~ & \textcolor{red}{ \text{ Original equation.}} \\ -0.35 \left( \frac{x}{-0.35} \right) = -0.35 (4.2) ~ & \textcolor{red}{ \text{ Multiply both sides by } -0.35.} \\ x = -1.470 ~ & \textcolor{red}{ \text{ Simplify: } -0.35 (4.2) = -1.470.} \end{aligned}\nonumber \]

Ejercicio

Resolver para y:$\frac{y}{0.37} = -1.52$.

Contestar: −0.5624

Todavía podemos dividir ambos lados de una ecuación por el mismo número decimal sin afectar la solución.

Ejemplo 3

Resolver para x:$−1.2x = −4.08$.

Solución

Para deshacer multiplicando por −1.2, divida ambos lados de la ecuación por −1.2.

\[ \begin{aligned} -1.2x = -4.08 ~ & \textcolor{red}{ \text{ Original equation.}} \\ \frac{-1.2x}{-1.2} = \frac{-4.08}{-1.2} ~ & \textcolor{red}{ \text{ Divide both sides by } -1.2} \\ x = 3.4 ~ & \textcolor{red}{ \text{ Simplify: } -4.08/(-1.2)=3.4.} \end{aligned}\nonumber \]

Ejercicio

Resolver para z:$-2.5z=1.4$

Contestar: −0.56

Combinando Operaciones

A veces necesitamos combinar operaciones.

Ejemplo 4

Resolver para x:$−3.8x − 1.7 = −17.28$.

Solución

Para deshacer restar 1.7, suma 1.7 a ambos lados de la ecuación.

\[ \begin{aligned} -3.8x-1.7=-17.28 ~ & \textcolor{red}{ \text{ Original equation.}} \\ -3.8x-1.7+1.7=-17.28+1.7 ~ & \textcolor{red}{ \text{ Add 1.7 to both sides.}} \\ -3.8x=-15.58 ~ & \textcolor{red}{ \text{ Simplify: } -17.28 + 1.7 = -15.58.} \end{aligned}\nonumber \]

A continuación, para deshacer multiplicando por −3.8, divida ambos lados de la ecuación por −3.8.

\[ \begin{aligned} \frac{-3.8x}{-3.8} = \frac{-15.88}{-3.8} ~ & \textcolor{red}{ \text{ Divide both sides by } -3.8.} \\ x = 4.1 ~ & \textcolor{red}{ \text{ Simplify: } -15.58/(-3.8) = 4.1.} \end{aligned}\nonumber \]

Ejercicio

Resolver para u:$-0.02u-3.2=-1.75$.

Contestar: −72.5

Combinando términos similares

La combinación de términos similares con coeficientes decimales se realiza de la misma manera que combinar términos similares con coeficientes enteros.

Ejemplo 5

Simplificar la expresión:$−3.2x + 1.16x$.

Solución

Para combinar estos términos similares debemos sumar los coeficientes.

Para sumar coeficientes con signos diferentes, primero resta el coeficiente con la magnitud menor del coeficiente con la magnitud mayor.

\[\begin{array}{r} 3.20 \\ - 1.16 \\ \hline 2.04 \end{array}\nonumber \]

Prefijo el signo del número decimal que tiene la magnitud mayor. Por lo tanto:

\[−3.2+1.16 = −2.04.\nonumber \]

Ahora podemos combinar términos similares de la siguiente manera:

\[−3.2x + 1.16x = −2.04x\nonumber \]

Ejercicio

Simplificar:$-1.185t+3.2t$

Contestar: 2.015 t

A la hora de resolver ecuaciones, a veces necesitamos combinar términos similares.

Ejemplo 6

Resuelve la ecuación para x:$4.2 − 3.1x + 2x = −7.02$.

Solución

Combina términos similares en el lado izquierdo de la ecuación.

\[ \begin{aligned} 4.2-3.1x+2x=-7.02 ~ & \textcolor{red}{ \text{ Original equation.}} \\ 4.2 - 1.1x = -7.02 ~ & \textcolor{red}{ \text{ Combine like terms: } -3.1x + 2x = -1.1x.} \\ 4.2 - 1.1x - 4.2 = -7.02 - 4.2 ~ & \textcolor{red}{ \text{ Subtract 4.2 from both sides.}} \\ -1.1x = -11.02 ~ & \textcolor{red}{ \text{ Subtract: } -7.02 - 4.2 = -11.22.} \\ \frac{-1.1x}{-1.1} = \frac{-11.22}{-1.1} ~ & \textcolor{red}{ \text{ Divide both sides by } -1.1.} \\ x = 10.2 ~ & \textcolor{red}{ \text{ Divide: } -11.22/(-1.1) = 10.2.} \end{aligned}\nonumber \]

Así, la solución de la ecuación es 10.2.

Cheque

Como todas las ecuaciones, podemos verificar nuestra solución sustituyendo nuestra respuesta en la ecuación original.

\[ \begin{aligned} 4.2 - 3.1x +2x = -7.02 ~ & \textcolor{red}{ \text{ Original equation.}} \\ 4.2 - 3.1(10.2) + 2(10.2) = -7.02 ~ & \textcolor{red}{ \text{ Substitute 10.2 for } x.} \\ 4.2 - 31.62 + 20.4 = -7.02 ~ & \textcolor{red}{ \text{ Multiply: } 3.1(10.2) = 31.62, ~ 2(10.2) = 20.4.} \\ -27.42 + 20.4 = -7.02 ~ & \textcolor{red}{ \text{ Order of Ops: Add, left to right.}} \\ ~ & \textcolor{red}{ ~ 4.2 - 31.62 = -27.42.} \\ -7.02 = -7.02 ~ & \textcolor{red}{ \text{ Add: } -27.42 + 20.4 = -7.02.} \end{aligned}\nonumber \]

Debido a que la última línea es una declaración verdadera, la solución x = 10.2 comprueba.

Ejercicio

Resolver para r:$-4.2 + 3.6r - 4.1r = 1.86$

Contestar: −12.12

Uso de la propiedad distributiva

A veces necesitaremos emplear la propiedad distributiva a la hora de resolver ecuaciones.

Propiedad distributiva

Sea a, b y c cualquier número. Entonces,

\[a(b + c) = ab + ac.\nonumber \]

Ejemplo 7

Resuelve la ecuación para x:$−6.3x − 0.4(x − 1.2) = −0.86$.

Solución

Primero distribuimos −0.4 veces cada término entre paréntesis, luego combinamos términos similares.

\[ \begin{aligned} -6.3x - 0.4(x-1.2) = -0.86 ~ & \textcolor{red}{ \text{ Original equation.}} \\ -6.3x-0.4x+0.48 = -0.86 ~ & \textcolor{red}{ \text{ Distribute. Note that } -0.4(-1.2)=0.48.} \\ -6.7x+0.48=-0.86 ~ & \textcolor{red}{ \text{ Combine like terms.}} \end{aligned}\nonumber \]

A continuación, resta 0.48 de ambos lados, luego divide ambos lados de la ecuación resultante por −6.7.

\[ \begin{aligned} -6.7x+0.48-0.48 = -0.86 - 0.48 ~ & \textcolor{red}{ \text{ Subtract 0.48 from both sides.}} \\ -6.7x = -1.34 ~ & \textcolor{red}{ \text{ Simplify: } -0.86 - 0.48 = -1.34.} \\ \frac{-6.7x}{-6.7} = \frac{-1.34}{-6.7} ~ & \textcolor{red}{ \text{ Divide both sides by } -6.7.} \\ x = 0.2 ~ & \textcolor{red}{ \text{ Simplify: } -1.34/(-6.7)=0.2.} \end{aligned}\nonumber \]

Ejercicio

Resolver para x:$ −2.5x − 0.1(x − 2.3) = 8.03$

Contestar: −3

Soluciones de redondeo

En ocasiones una solución aproximada es adecuada.

Ejemplo$\PageIndex{1}$

Resuelve la ecuación$3.1x+ 4.6=2.5 − 2.2x$ para x. Redondea la respuesta a la décima más cercana.

Solución

Necesitamos aislar los términos que contienen x en un lado de la ecuación. Comenzamos sumando 2.2x a ambos lados de la ecuación.

\[ \begin{aligned} 3.1x + 4.6 = 2.5 - 2.2x ~ & \textcolor{red}{ \text{ Original equation.}} \\ 3.1x + 4.6 + 2.2x = 2.5 - 2.2x + 2.2x ~ & \textcolor{red}{ \text{ Add } 2.2x \text{ to both sides.}} \\ 5.3x + 4.6 = 2.5 ~ & \textcolor{red}{ \text{ Combine terms: } 3.1x + 2.2x = 5.3x.} \end{aligned{\nonumber \]

Necesitamos aislar los términos que contienen x en un lado de la ecuación. Comenzamos sumando 2.2x a ambos lados de la ecuación.

\[ \begin{aligned} 5.3x + 4.6 - 4.6 = 2.5 - 4.6 ~ & \textcolor{red}{ \text{ Subtract 4.6 from both sides.}} \\ 5.3x = -2.1 ~ & \textcolor{red}{ \text{ Simplify: } 2.5 - 4.6 = -2.1.} \end{aligned}\nonumber \]

Para deshacer el efecto de multiplicar por 5.3, divida ambos lados de la ecuación por 5.3.

\[ \begin{aligned} \frac{5.3x}{5.3} = \frac{-2.1}{5.3} ~ & \textcolor{red}{ \text{Divide both side by 5.3.}} \\ x \approx -0.4 ~ & \textcolor{red}{ \text{ Round solution to nearest tenth.}} \end{aligned}\nonumber \]

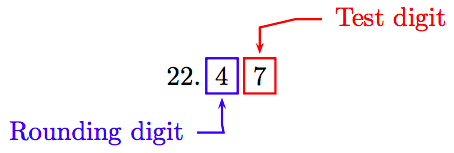
Para redondear la respuesta a la décima más cercana, debemos llevar a cabo la división un lugar adicional.

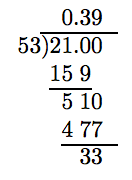
$Screen Shot 2019-09-11 en 4.43.18 PM.png$

Debido a que el “dígito de prueba” es mayor o igual a 5, agregue 1 al dígito de redondeo y trunca.

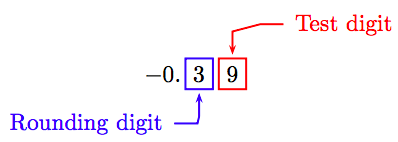
$Screen Shot 2019-09-11 en 4.43.23 PM.png$

Así, −0.39 ≈ −0.4.

Así, −2.1/5.3 ≈ −0.39.

Ejercicio

Resolver para x:$4.2x − 1.25 = 3.4+0.71x$

Contestar: 1.33

Aplicaciones

Veamos algunas aplicaciones que involucran ecuaciones que contienen decimales. Para mayor comodidad, repetimos los Requisitos para Soluciones de Problemas de Word.

Requisitos para soluciones de problemas verbales

Configura un Diccionario de Variables. Debes dejar saber a tus lectores qué representa cada variable en tu problema. Esto se puede lograr de varias maneras:
1. Declaraciones como “Que P represente el perímetro del rectángulo”.
2. Etiquetar valores desconocidos con variables en una tabla.
3. Etiquetar cantidades desconocidas en un boceto o diagrama.
Configura una Ecuación. Toda solución a un problema de palabras debe incluir una ecuación cuidadosamente elaborada que describa con precisión las restricciones en la declaración del problema.
Resuelve la Ecuación. Siempre debes resolver la ecuación establecida en el paso anterior.
Responda a la Pregunta. Este paso se pasa por alto fácilmente. Por ejemplo, el problema podría preguntar por la edad de Jane, pero la solución de tu ecuación da la edad de la hermana de Jane, Liz. Asegúrate de responder la pregunta original hecha en el problema. Su solución debe escribirse en una oración con las unidades correspondientes.
Mira hacia atrás. Es importante señalar que este paso no implica que simplemente deba verificar su solución en su ecuación. Después de todo, es posible que tu ecuación modele incorrectamente la situación del problema, por lo que podrías tener una solución válida a una ecuación incorrecta. La pregunta importante es: “¿Tiene sentido tu respuesta con base en las palabras de la declaración original del problema?”

Empecemos con un problema de jardín rectangular.

Ejemplo 9

Molly necesita crear una parcela de jardín rectangular que cubra 200 metros cuadrados (200 m ²). Si el ancho de la parcela es de 8.9 metros, encuentra la longitud de la parcela correcta a la décima de metro más cercana.

Solución

Seguiremos los Requisitos para Soluciones de Problemas de Word.

1. Configura un Diccionario de Variables. Usaremos un boceto para definir nuestras variables.

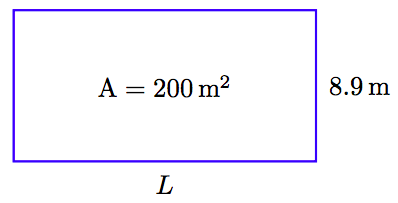
$Screen Shot 2019-09-11 en 4.51.36 PM.png$

Tenga en cuenta que L representa la longitud del rectángulo.

2. Configura una ecuación. El área A de un rectángulo viene dada por la fórmula

\[A = LW,\nonumber \]

donde L y W representan el largo y ancho del rectángulo, respectivamente. Sustituye 200 por A y 8.9 por W en la fórmula para obtener

\[200 = L(8.9),\nonumber \]

o equivalentemente,

\[200 = 8.9L.\nonumber \]

3. Resuelve la Ecuación. Divide ambos lados de la última ecuación por 8.9, luego redondea tu respuesta a la décima más cercana.

\[ \begin{aligned} \frac{200}{8.9} = \frac{8.9L}{8.9} ~ & \textcolor{red}{ \text{ Divide both sides by 8.9.}} \\ 22.5 \approx L ~ & \textcolor{red}{ \text{ Round to nearest tenth.}} \end{aligned}\nonumber \]

Para redondear la respuesta a la décima más cercana, debemos llevar a cabo la división un lugar adicional.

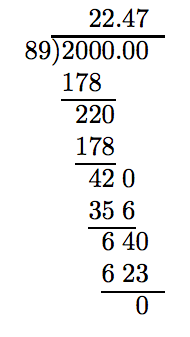
$Screen Shot 2019-09-11 en 4.51.44 PM.png$

Debido a que el “dígito de prueba” es mayor o igual a 5, agregue 1 al dígito de redondeo y trunca.

$Screen Shot 2019-09-11 en 4.51.49 PM.png$

Así, 200/8.9 ≈ 22.5.

4. Responda a la Pregunta. A la décima de metro más cercana, la longitud de la parcela rectangular es L ≈ 22.5 metros.

5. Mira hacia atrás. Tenemos L ≈ 22.5 metros y W = 8.9 metros. Multiplica la longitud y el ancho para encontrar el área.

\[\text{Area} \approx (22.5 \text{ m})(8.9 \text{ m}) ≈ 200.25 \text{ m}^2.\nonumber \]

Tenga en cuenta que esta es muy cerca del área exacta de 200 metros cuadrados. La discrepancia se debe a que encontramos la longitud redondeada a la décima de metro más cercana

Ejercicio

La carrera de perros de Eta tiene la forma de un rectángulo con un área de 500 pies cuadrados. Si el largo de la carrera es de 28 pies, encuentra el ancho de la carrera, correcto a la décima de pie más cercana.

Contestar: 17.9 pies

Ejemplo 10

Boletos infantiles al circo salen a la venta por $6.75. El club Boys and Girls de Eureka tiene $1,000 reservados para adquirir estos boletos. Aproximadamente, ¿cuántos boletos puede adquirir el club Girls and Boys?

Solución

Seguiremos los Requisitos para Soluciones de Problemas de Word.

1. Configura un Diccionario de Variables. Que N represente el número de boletos comprados por el club Boys and Girls de Eureka.

2. Configura una ecuación. Tenga en cuenta que

\[ \begin{matrix} \colorbox{cyan}{Price per ticket} & \text{ times } & \colorbox{cyan}{Number of tickets} & \text{ is } & \colorbox{cyan}{Full Purchase Price} \\ 6.75 & . & N & = & 1,000 \end{matrix}\nonumber \]

De ahí que nuestra ecuación sea 6.75 N = 1000.

3. Resuelve la Ecuación. Divide ambos lados de la ecuación entre 6.75.

\[ \begin{aligned} \frac{6.75N}{6.75} = \frac{1000}{6.75} ~ & \textcolor{red}{ \text{ Divide both sides by 6.75.}} \\ N \approx 148 ~ & \textcolor{red}{ \text{ Truncate to nearest unit.}} \end{aligned}\nonumber \]

Empuje el punto decimal al extremo derecho del divisor y el punto decimal en el dividendo un número igual de lugares.

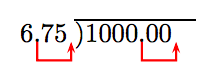
$Captación de pantalla 2019-09-11 al 5.05.02 PM.png$

Detendremos la división en la posición de las unidades.

$Captación de pantalla 2019-09-11 al 5.05.05 PM.png$

4. Responda a la Pregunta. El club Boys and Girls puede adquirir 148 boletos.

5. Mira hacia atrás. Calculemos el costo de 148 boletos a $6.75 cada uno.

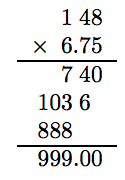
$Screen Shot 2019-09-11 a las 5.06.55 PM.png$

Así, a $6.75 cada uno, 148 boletos costarán $999. Debido a que el club Boys and Girls de Eureka tiene $1,000 para trabajar, tenga en cuenta que al club no le queda suficiente dinero para otro boleto.

Ejercicio

Los boletos para adultos al circo cuestan $12.25 cada uno. Si el club tiene $1,200 reservados para la compra de boletos de adulto, ¿cuántos boletos de adulto pueden comprar?

Contestar: 97

Ejemplo 11

Marta tiene 20 pies de cercado decorativo que utilizará para el borde de un pequeño jardín circular. Encuentra el diámetro del jardín circular, correcto a la centésima de pie más cercana. Usar π ≈ 3.14.

Solución

La fórmula que rige la relación entre la circunferencia y el diámetro de un círculo es

\[C = \pi d\nonumber \]

Los 20 pies de cercado decorativo serán la circunferencia del jardín circular. Sustituir 20 por C y 3.14 por π.

\[20 = 3.14d\nonumber \]

Divide ambos lados de la ecuación entre 3.14.

\[ \begin{aligned} \frac{20}{3.14} = \frac{3.14d}{3.14} \\ \frac{20}{3.14} = d \end{aligned}\nonumber \]

Mueve el punto decimal hasta el final del divisor, luego mueve el punto decimal en el dividendo un número igual de lugares (dos lugares) a la derecha. Tenga en cuenta que debemos sumar dos ceros finales en el dividendo.

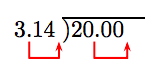
$Captación de pantalla 2019-09-11 al 5.09.59 PM.png$

Así, el problema se convierte en:

\[ 314 \overline{ )2000}\nonumber \]

Tenemos que redondear a la centésima más cercana. Esto requiere que llevemos la división un lugar adicional a la derecha del lugar centésimas (es decir, al lugar milésimas).

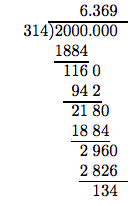
$Captación de pantalla 2019-09-16 en 2.02.59 PM.png$

Para el paso final, debemos redondear 6.369 a la centésima más cercana. En el esquema que sigue, hemos encajonado el dígito de centésimas (el “dígito de redondeo”) y el “dígito de prueba” que sigue al “dígito de redondeo”.

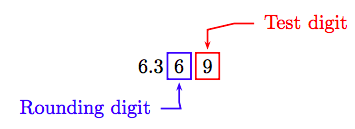
$Captación de pantalla 2019-09-16 en 2.03.52 PM.png$

Debido a que el “dígito de prueba” es mayor o igual a 5, agregamos 1 al “dígito de redondeo”, luego truncamos. Por lo tanto, a la centésima de pie más cercana, el diámetro del círculo es aproximadamente

\[d ≈ 6.37 \text{ ft.}\nonumber \]

Ejercicio

Dylan tiene una pluma circular para perros con circunferencia de 100 pies. Encuentra el radio de la pluma, correcto a la décima de pie más cercana. Usar π ≈ 3.14.

Contestar: 15.9 pies

Ejercicios

En los Ejercicios 1-16, resuelve la ecuación.

1. $5.57x − 2.45x = 5.46$

2. $−0.3x − 6.5x = 3.4$

3. $−5.8x + 0.32 + 0.2x = −6.96$

4. $−2.2x − 0.8 − 7.8x = −3.3$

5. $−4.9x + 88.2 = 24.5$

6. $−0.2x − 32.71 = 57.61$

7. $0.35x − 63.58 = 55.14$

8. $−0.2x − 67.3 = 93.5$

9. $−10.3x + 82.4=0$

10. $−1.33x − 45.22 = 0$

11. $−12.5x + 13.5=0$

12. $44.15x − 8.83 = 0$

13. $7.3x − 8.9 − 8.34x = 2.8$

14. $0.9x + 4.5 − 0.5x = 3.5$

15. $−0.2x + 2.2x = 6.8$

16. $−7.9x + 2.9x = 8.6$

En los Ejercicios 17-34, resuelve la ecuación.

17. $6.24x − 5.2=5.2x$

18. $−0.6x + 6.3=1.5x$

19. $−0.7x − 2.4 = −3.7x − 8.91$

20. $3.4x − 4.89 = 2.9x + 3.6$

21. $−4.9x = −5.4x + 8.4$

22. $2.5x = 4.5x + 5.8$

23. $−2.8x = −2.3x − 6.5$

24. $1.2x = 0.35x − 1.36$

25. $−2.97x − 2.6 = −3.47x + 7.47$

26. $−8.6x − 2.62 = −7.1x + 8.54$

27. $−1.7x = −0.2x − 0.6$

28. $3.89x = −5.11x + 5.4$

29. $−1.02x + 7.08 = −2.79x$

30. $1.5x − 2.4=0.3x$

31. $−4.75x − 6.77 = −7.45x + 3.49$

32. $−1.2x − 2.8 = −0.7x − 5.6$

33. $−4.06x − 7.38 = 4.94x$

34. $−4.22x + 7.8 = −6.3x$

En los Ejercicios 35-52, resuelve la ecuación.

35. $2.3+0.1(x + 2.9) = 6.9$

36. $−6.37 + 6.3(x + 4.9) = −1.33$

37. $0.5(1.5x − 6.58) = 6.88$

38. $0.5(−2.5x − 4.7) = 16.9$

39. $−6.3x − 0.4(x − 1.8) = −16.03$

40. $−2.8x + 5.08(x − 4.84) = 19.85$

41. $2.4(0.3x + 3.2) = −11.4$

42. $−0.7(0.2x + 5.48) = 16.45$

43. $−0.8(0.3x + 0.4) = −11.3$

44. $7.5(4.4x + 7.88) = 17.19$

45. $−7.57 − 2.42(x + 5.54) = 6.95$

46. $5.9 − 0.5(x + 5.8) = 12.15$

47. $−1.7 − 5.56(x + 6.1) = 12.2$

48. $−7.93 + 0.01(x + 7.9) = 14.2$

49. $4.3x − 0.7(x + 2.1) = 8.61$

50. $1.5x − 4.5(x + 4.92) = 15.6$

51. $−4.8x + 3.3(x − 0.4) = −7.05$

52. $−1.1x + 1.3(x + 1.3) = 19.88$

En los Ejercicios 53-58, resuelve la ecuación.

53. $0.9(6.2x − 5.9) = 3.4(3.7x + 4.3) − 1.8$

54. $0.4(−4.6x+ 4.7) = −1.6(−2.2x+ 6.9)−4.5$

55. $−1.8(−1.6x + 1.7) = −1.8(−3.6x − 4.1)$

56. $−3.3(−6.3x + 4.2) − 5.3=1.7(6.2x + 3.2)$

57. $0.9(0.4x + 2.5) − 2.5 = −1.9(0.8x + 3.1)$

58. $5.5(6.7x + 7.3) = −5.5(−4.2x + 2.2)$

59. Stacy dirige un negocio en su casa haciendo casas para pájaros. Cada mes tiene costos fijos de $200. Además, por cada casa para pájaros que haga, incurre en un costo adicional de $3.00. Si sus costos totales para el mes fueron de $296.00, ¿cuántas casas para pájaros hizo?

60. Stella dirige un negocio fuera de su casa haciendo cortinas. Cada mes tiene costos fijos de 175 dólares. Además, por cada cortina que hace, incurre en un costo adicional de $2.75. Si sus costos totales para el mes fueron de 274.00 dólares, ¿cuántas cortinas hizo?

61. Una tienda de papelería cuenta con grapadoras a la venta por $1.50 cada una. Una empresa compra un número desconocido de estos y el costo total de su compra es de $36.00. ¿Cuántos fueron comprados?

62. Una tienda de papelería tiene paquetes de CD a la venta por $2.50 cada uno. Una empresa compra un número desconocido de estos y el costo total de su compra es de $40.00. ¿Cuántos fueron comprados?

63. Julie dirige un negocio en su casa haciendo manteles. Cada mes tiene costos fijos de $100. Además, por cada mantel que fabrica incurre en un costo adicional de $2.75. Si sus costos totales para el mes fueron de 221.00 dólares, ¿cuántos manteles hizo?

64. Stella dirige un negocio fuera de su casa haciendo colchas. Cada mes tiene costos fijos de $200. Además, por cada colcha que hace, incurre en un costo adicional de $1.75. Si sus costos totales para el mes fueron de 280.50 dólares, ¿cuántos edredones hizo?

65. Marta tiene 60 pies de cercado decorativo que utilizará para el borde de un pequeño jardín circular. Encuentra el diámetro del jardín circular, correcto a la centésima de pie más cercana. Usar π ≈ 3.14.

66. Trinity tiene 44 pies de cercado decorativo que utilizará para el borde de un pequeño jardín circular. Encuentra el diámetro del jardín circular, correcto a la centésima de pie más cercana. Usar π ≈ 3.14.

67. Boletos infantiles a los capades de hielo salen a la venta por $4.25. El YMCA de Sacramento tiene $1,000 reservados para comprar estos boletos. Aproximadamente ¿cuántos boletos puede adquirir el YMCA de Sacramento?

68. Boletos infantiles a los capades de hielo salen a la venta por $5. Caballeros de Colón tiene $1,200 reservados para adquirir estos boletos. Aproximadamente ¿cuántos boletos pueden adquirir Caballeros de Colón?

69. Una tienda de papelería cuenta con lápices mecánicos a la venta por $2.25 cada uno. Una empresa compra un número desconocido de estos y el costo total de su compra es de 65.25 dólares. ¿Cuántos fueron comprados?

70. Una tienda de papelería tiene plantillas de ingeniería a la venta por $2.50 cada una. Una empresa compra un número desconocido de estos y el costo total de su compra es de $60.00. ¿Cuántos fueron comprados?

71. Marta tiene 61 pies de cercado decorativo que utilizará para el borde de un pequeño jardín circular. Encuentra el diámetro del jardín circular, correcto a la centésima de pie más cercana. Usar π ≈ 3.14.

72. Kathy tiene 86 pies de cercado decorativo que utilizará para el borde de un pequeño jardín circular. Encuentra el diámetro del jardín circular, correcto a la centésima de pie más cercana. Usar π ≈ 3.14.

73. Kathy necesita crear una parcela de jardín rectangular que cubra 100 metros cuadrados (100 m ²). Si el ancho de la parcela es de 7.5 metros, encuentra la longitud de la parcela correcta a la décima de metro más cercana.

74. Marianne necesita crear una parcela de jardín rectangular que cubra 223 metros cuadrados (223 m ²). Si el ancho de la parcela es de 8.3 metros, encuentra la longitud de la parcela correcta a la décima de metro más cercana.

75. Los boletos infantiles para las carreras de autos stock salen a la venta por $4.5. El club Boys and Girls de Eureka tiene $1,300 reservados para adquirir estos boletos. Aproximadamente ¿cuántos boletos puede adquirir el club Boys and Girls de Eureka?

76. Los boletos infantiles al cine salen a la venta por $4.75. El club de Leones de la Alameda tiene $800 reservados para adquirir estos boletos. Aproximadamente ¿cuántos boletos puede adquirir el club de Leones de la Alameda?

77. Ashley necesita crear una parcela de jardín rectangular que cubra 115 metros cuadrados (115 m ²). Si el ancho de la parcela es de 6.8 metros, encuentra la longitud de la parcela correcta a la décima de metro más cercana.

78. Molly necesita crear una parcela de jardín rectangular que cubra 268 metros cuadrados (268 m ²). Si el ancho de la parcela es de 6.1 metros, encuentra la longitud de la parcela correcta a la décima de metro más cercana.

79. Inventario de Crudo. Los inventarios comerciales de crudo de Estados Unidos disminuyeron 3.8 millones de barriles en la semana que finalizó el 19 de junio. Si hubo 353.9 millones de barriles a la semana siguiente, ¿cuáles eran los inventarios de crudo antes de la caída? rttnews.com 24/09

80. Indocumentados. En 2008, California tenía 2.7 millones de residentes indocumentados. Esto es el doble del número en 1990. ¿Cuántos residentes indocumentados había en California en 1990? Horarios de Prensa Asociados-Estándar 4/15/09

81. Diamantes Brillantes. El índice de refracción n indica el número de veces más lento que una onda de luz viaja en un medio particular que viaja en vacío. Un diamante tiene un índice de refracción de 2.4. Esto es aproximadamente una y un cuarto veces mayor que el índice de refracción de un circón. ¿Cuál es el índice de refracción de un circón? Redondee su resultado a la décima más cercana.

RESPUESTAS

1. 1.75

3. 1.3

5. 13

7. 339.2

9. 8

11. 1.08

13. −11.25

15. 3.4

17. 5

19. −2.17

21. 16.8

23. 13

25. 20.14

27. 0.4

29. −4

31. 3.8

33. −0.82

35. 43.1

37. 13.56

39. 2.5

41. −26.5

43. 45.75

45. −11.54

47. −8.6

49. 2.8

51. 3.82

53. −2.59

55. −2.9

57. −3

59. 32

61. 24

63. 44

65. 19.11 pies

67. 235 boletos

69. 29

71. 19.43 pies

73. 13.3 metros

75. 288 boletos

77. 16.9 metros

79. 357.7 millones de barriles

81. 1.9

Search

Text Color

Text Size

Margin Size

Font Type