5.2: Introducción a los decimales

Última actualización
Guardar como PDF

Page ID: 113422

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Recordemos que los números enteros se construyen usando dígitos.

Los Dígitos

El conjunto

\[ {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} \nonumber\nonumber \]

se llama el conjunto de dígitos.

A modo de ejemplo, el número entero 55,555 (“cincuenta y cinco mil quinientos cincuenta y cinco”) se construye utilizando un solo dígito. No obstante, la posición del dígito 5 determina su valor en el número 55,555. La primera ocurrencia de la

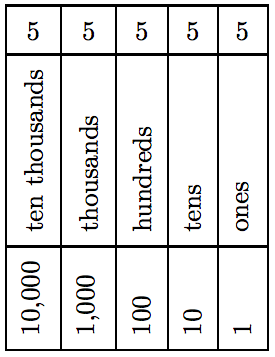
$Screen Shot 2019-09-09 at 1.49.36 PM.png$

Cuadro 5.1: Valor posicional.

dígito 5 ocurre en el lugar de los diez miles, por lo que su valor es de 5 diez miles, o 50,000. La siguiente ocurrencia del dígito 5 está en el lugar de miles, por lo que su valor es de 5 miles, o 5,000. En efecto, el número entero 55,555 en forma expandida es

50000 + 5000 + 500 + 50 + 5

que refleja el valor del dígito 5 en cada lugar.

Notación decimal

En la Tabla 5.1, cada vez que mueve una columna hacia la izquierda, el valor posicional es 10 veces mayor que el valor posicional de la columna anterior. Viceversa, cada vez que mueves una columna hacia la derecha, el valor posicional es 1/10 del valor posicional de la columna anterior.

Ahora, consideremos el número decimal 12.3456, que consta de tres partes: la parte del número entero, el punto decimal y la parte fraccionaria.

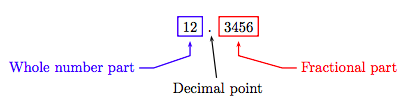
$Screen Shot 2019-09-09 at 1.50.55 PM.png$

La parte del número entero del número decimal es la parte que se encuentra estrictamente a la izquierda del punto decimal, y el valor posicional de cada dígito en la parte del número entero viene dado por las columnas que se muestran en la Tabla 5.1.

La parte fraccionaria del número decimal es la parte que se encuentra estrictamente a la derecha del punto decimal. Como vimos en la Tabla 5.1, cada columna tiene un valor igual a 1/10 del valor de la columna que se encuentra a su izquierda inmediata. Así, no debería sorprendernos que:

La primera columna a la derecha del punto decimal tiene el valor posicional 1/10 (décimas).
La segunda columna a la derecha del punto decimal tiene un valor posicional 1/100 (centésimas).
La tercera columna a la derecha del punto decimal tiene un valor posicional 1/1000 (milésimas).
La cuarta columna a la derecha del punto decimal tiene un valor posicional 1/10000 (diez milésimas).

Estos resultados se resumen para el número decimal 12.3456 en la Tabla 5.2.

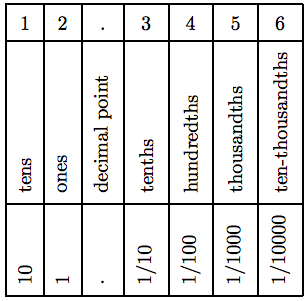
$Screen Shot 2019-09-09 at 1.51.59 PM.png$

Cuadro 5.2: Valor posicional.

Pronunciar números decimales

El número decimal 12.3456 está compuesto por 1 diez, 2 unos, 3 décimas, 4 centésimas, 5 milésimas y 6 diezmilésimas (ver Tabla 5.2), y puede escribirse en forma expandida como

\[12.3456 = 10 + 2 + \frac{3}{10} + \frac{4}{100} + \frac{5}{1000} + \frac{6}{10000}.\nonumber \]

Tenga en cuenta que los números enteros se pueden combinar y las fracciones se pueden escribir con un denominador común y sumar.

\[ \begin{aligned} 12.3456 & = 12 + \frac{3 \cdot \textcolor{red}{1000}}{10 \cdot \textcolor{red}{1000}} + \frac{4 \cdot \textcolor{red}{100}}{100 \cdot \textcolor{red}{100}} + \frac{5 \cdot \textcolor{red}{10}}{1000 \cdot \textcolor{10}} + \frac{6}{10000} \\ & = 12 + \frac{3000}{10000} + \frac{400}{10000} + \frac{50}{10000} + \frac{6}{10000} \\ & = 12 + \frac{3456}{10000} \end{aligned}\nonumber \]

El resultado nos dice cómo pronunciar el número 12.3456. Se pronuncia “doce y tres mil cuatrocientos cincuenta y seis diez milésimas”.

Ejemplo 1

Coloque el número decimal 1,234.56 en forma expandida, luego combine la parte del número entero y sume la parte fraccionaria sobre un denominador común. Usa el resultado para ayudar a pronunciar el número decimal.

Solución

En forma ampliada,

\[1, 234.56 = 1, 000 + 200 + 30 + 4 + \frac{5}{10} + \frac{6}{100}\nonumber \]

Suma el número entero de partes. Exprese las partes fraccionarias como fracciones equivalentes y combine sobre un denominador común.

\[ \begin{aligned} = 1,234 + \frac{5 \cdot \textcolor{10}}{10 \cdot \textcolor{red}{10}} + \frac{6}{100} \\ = 1,234 + \frac{50}{100} + \frac{6}{100} \\ = 1, 234 + \frac{56}{100} \end{aligned}\nonumber \]

De ahí que mil 234.56 se pronuncia “mil doscientos treinta y cuatro cincuenta y seis centésimas”.

Ejercicio

Coloque el número decimal 3,502.23 en forma expandida, luego combine la parte del número entero y sume la parte fraccionaria sobre un denominador común.

Contestar: $3,502 + \frac{23}{100}$

Ejemplo 2

Coloque el número decimal 56.128 en forma expandida, luego combine la parte del número entero y sume la parte fraccionaria sobre un denominador común. Usa el resultado para ayudar a pronunciar el número decimal.

Solución

En forma ampliada,

\[56.128 = 50 + 6 + \frac{1}{10} + \frac{2}{100} + \frac{8}{1000}\nonumber \]

Suma el número entero de partes. Exprese las partes fraccionarias como fracciones equivalentes y combine sobre un denominador común.

\[ \begin{aligned} = 56 + \frac{1 \cdot \textcolor{red}{100}}{10 \cdot \textcolor{red}{100}} + \frac{2 \cdot \textcolor{red}{10}}{100 \cdot \textcolor{red}{10}} + \frac{8}{1000} \\ = 56 + \frac{100}{1000} + \frac{20}{1000} + \frac{8}{1000} \\ = 56 + \frac{128}{1000} \end{aligned}\nonumber \]

Así, 56.128 se pronuncia “cincuenta y seis ciento veintiocho milésimas”.

Ejercicio

Coloque el número decimal 235.568 en forma expandida, luego combine la parte del número entero y sume la parte fraccionaria sobre un denominador común.

Contestar: $235 + \frac{568}{1000}$

La discusión y el ejemplo llevan al siguiente resultado.

Cómo leer un número decimal

Pronunciar la parte del número entero a la izquierda del decimal como lo haría con cualquier número entero.
Decir la palabra “y” para el punto decimal.
Indique la parte fraccionaria a la derecha del decimal como lo haría con cualquier número entero, seguido del valor posicional del dígito en la columna más a la derecha.

Ejemplo 3

Pronunciar el número decimal 34.12.

Solución

El dígito más a la derecha en la parte fraccionaria de 34.12 está en la columna de centésimas. Así, 34.12 se pronuncia “treinta y cuatro y doce centésimas”.

Ejercicio

Pronuncia 28.73

Contestar: “Veintiocho y setenta y tres centésimas”

Punto Importante

Al pronunciar números decimales, el punto decimal se lee como “y”. Ninguna otra instancia de la palabra “y” debería aparecer en la pronunciación.

Ejemplo 4

Explique por qué “cuatrocientos treinta y cuatro y dos décimas” es una pronunciación incorrecta del número decimal 434.2.

Solución

El punto decimal se lee como “y”. No se permite otra ocurrencia de la palabra “y” en la pronunciación. La pronunciación correcta debe ser “cuatrocientos treinta y cuatro y dos décimas”.

Ejercicio

Pronuncia 286.9.

Contestar: “Cuatrocientos treinta y cuatro y dos décimas”

Ejemplo 5

Pronunciar el número decimal 5,678.123.

Solución

El dígito más a la derecha en la parte fraccionaria de 5,678.123 se encuentra en la columna milésimas. De ahí que 5 mil 678.123 se pronuncia “5 mil seiscientos setenta y ocho y ciento veintitrés milésimas”.

Ejercicio

Pronuncia 7, 002.207

Contestar: Respuesta: “Siete mil dos doscientos siete milésimas”.

Ejemplo 6

Pronunciar el número decimal 995.4325.

Solución

El dígito más a la derecha en la parte fraccionaria de 995.4325 está en la columna de las diez milésimas. De ahí que 995.4325 se pronuncia “novecientos noventa y cinco y cuatro mil trescientos veinticinco diez milésimas”.

Ejercicio

Pronuncia 500.1205.

Contestar: Respuesta: “Quinientos mil doscientos cinco diezmilésimas”.

Decimales a Fracciones

Debido a que ahora tenemos la capacidad de pronunciar números decimales, es un ejercicio sencillo cambiar un decimal a una fracción. ¹ Por ejemplo, 134.12 se pronuncia “ciento treinta y cuatro doce centésimas”, por lo que se puede escribir fácilmente como una fracción mixta.

\[134.12 = 134 \frac{12}{100}\nonumber \]

Pero esta fracción mixta se puede cambiar a una fracción impropia.

\[ \begin{aligned} 134 \frac{12}{100} \\ & = \frac{100 \cdot 134 + 12}{100} & = \frac{13400 + 12}{100} \\ * = \frac{13412}{100} \end{aligned}\nonumber \]

Tenga en cuenta que el numerador es nuestro número original sin el punto decimal. Hay dos decimales en el número original y el denominador de la fracción impropia final contiene dos ceros.

Esta discusión lleva al siguiente resultado.

¹ El cambio de fracciones a decimales se cubrirá en la Sección 5.5.

Cambio de decimales a fracciones impropias

Para cambiar un número decimal a una fracción impropia, proceda de la siguiente manera:

Crear una fracción.
Coloque el número decimal en el numerador sin el punto decimal.
Contar el número de decimales. Colocar un número igual de ceros en el denominador.

Ejemplo 7

Cambiar los siguientes números decimales a fracciones impropias: (a) 1.2345, y (b) 27.198.

Solución

En cada caso, coloque el número en el numerador sin el punto decimal. En el denominador, suma un número de ceros igual al número de decimales.

a) El número decimal 1.2345 tiene cuatro decimales. De ahí que,

\[1.2345 = \frac{12345}{10000}\nonumber \]

b) El número decimal 27.198 tiene tres decimales. De ahí que,

\[27.198 = \frac{27198}{1000}\nonumber \]

Ejercicio

Cambia 17.205 a una fracción impropia.

Contestar: $\frac{17205}{100}$

Ejemplo 8

Cambiar cada uno de los siguientes decimales a fracciones reducidas a términos más bajos: (a) 0.35, y (b) 0.125.

Solución

Colocar cada número en el numerador sin el punto decimal. Colocar un número de ceros en el denominador igual al número de decimales. Reducir a los términos más bajos.

a) Primero, colocar 35 sobre 100.

\[0.35 = \frac{35}{100}\nonumber \]

Podemos dividir tanto el numerador como el denominador por el mayor divisor común.

\[ \begin{aligned} = \frac{35 \div 5}{100 \div 5} ~ & \textcolor{red}{ \text{ Divide numerator and denominator by 5.}} \\ = \frac{7}{20} ~ & \textcolor{red}{ \text{ Simplify numerator and denominator.}} \end{aligned}\nonumber \]

b) Primero, colocar 125 sobre 1000.

\[0.125 = \frac{125}{1000}\nonumber \]

Factor primo y cancelar factores comunes.

\[ \begin{aligned} = \frac{5 \cdot 5 \cdot 5}{2 \cdot 2 \cdot 2 \cdot 5 \cdot 5 \cdot 5} ~ & \textcolor{red}{ \text{ Prime factor numerator and denominator.}} \\ = \frac{ \cancel{5} \cdot \cancel{5} \cdot \cancel{5}}{2 \cdot 2 \cdot 2 \cdot \cancel{5} \cdot \cancel{5} \cdot \cancel{5}} ~ & \textcolor{red}{ \text{ Cancel common factors.}} \\ = \frac{1}{8} ~ & \textcolor{red}{ \text{ Simplify.}} \end{aligned}\nonumber \]

Ejercicio

Cambiar 0.375 a una fracción, reducida a términos más bajos.

Contestar: 3/8

Redondeo

Las reglas para redondear números decimales son casi idénticas a las reglas para redondear números enteros. Primero, un poco de terminología.

Dígito de redondeo y dígito

El dígito en el lugar al que deseamos redondear se llama dígito de redondeo y el dígito que sigue a su derecha inmediata se llama dígito de prueba.

Si queremos redondear el número decimal 12.254 a la centésima más cercana, entonces el dígito de redondeo es 5 y el dígito de prueba es 4.

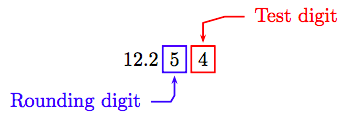
$Screen Shot 2019-09-09 at 2.32.22 PM.png$

Si usáramos las reglas para redondear números enteros, porque el dígito de prueba 4 es menor que 5, reemplazaríamos todos los dígitos a la derecha del dígito de redondeo por ceros para obtener la siguiente aproximación.

12.254 ≈ 12.250

Sin embargo, porque

\[12.250 = 12 \frac{250}{1000} = 12 \frac{25}{100},\nonumber \]

el cero final al final de la parte fraccional es irrelevante. De ahí que trunca cada dígito después del dígito de redondeo y usamos la siguiente aproximación.

12.254 ≈ 12.25

Observación Importante

Eliminar ceros finales del final de la parte fraccionaria de un número decimal no cambia su valor.

La discusión anterior motiva el siguiente algoritmo para redondear números decimales.

Redondeo de números decimales

Localiza el dígito redondeado y el dígito de prueba.

Si el dígito de prueba es mayor o igual a 5, agregue 1 al dígito de redondeo y trunca todos los dígitos a la derecha del dígito de redondeo.
Si el dígito de prueba es menor que 5, simplemente trunca todos los dígitos a la derecha del dígito de redondeo.

Ejemplo 9

Vuelta 8.7463 a la centésima más cercana.

Solución

Localice el dígito de redondeo en el lugar de centésimas y el dígito de prueba a su derecha inmediata.

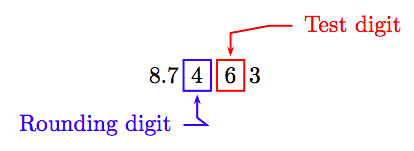
alt $Screen Shot 2019-09-09 at 2.38.01 PM.png$

Debido a que el dígito de prueba es mayor que 5, agregue 1 al dígito de redondeo y trunca todos los dígitos a la derecha del dígito de redondeo. De ahí, a la centésima más cercana:

8.7463 ≈ 8.75

Ejercicio

Vuelta 9.2768 a la centésima más cercana.

Contestar: 9.28

Ejemplo 10

Vuelta 113.246 a la décima más cercana.

Solución

Localice el dígito de redondeo en el lugar décimas y el dígito de prueba a su derecha inmediata.

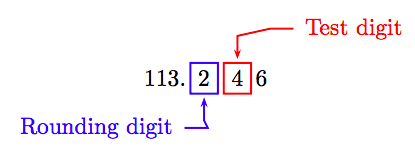
$Screen Shot 2019-09-09 at 2.38.08 PM.png$

Debido a que el dígito de prueba es menor que 5, trunca todos los dígitos a la derecha del dígito de redondeo. De ahí, a la décima más cercana:

113.246 ≈ 113.2

Ejercicio

Vuelta 58.748 a la décima más cercana.

Contestar: 58.7

Comparando decimales

Podemos comparar dos decimales positivos comparando dígitos en cada lugar a medida que nos movemos de izquierda a derecha, lugar por lugar. Por ejemplo, supongamos que deseamos comparar los números decimales 5.234 y 5.2357. Primero, agregue suficientes ceros finales al número decimal con menos lugares decimales para que los números tengan el mismo número de decimales. En este caso, tenga en cuenta que

\[ 5.234 = 5 \frac{234}{1000} = 5 \frac{2340}{10000} = 5.2340.\nonumber \]

Observación Importante

Agregar ceros finales al final de la parte fraccionaria de un número decimal no cambia su valor.

A continuación, alinee los números de la siguiente manera.

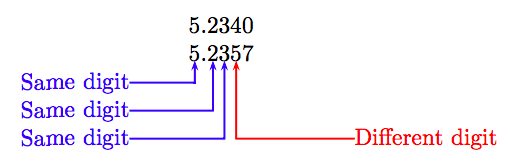
$Screen Shot 2019-09-09 at 2.38.16 PM.png$

Al escanear las columnas, moviéndose de izquierda a derecha, el primer lugar que tiene diferentes dígitos ocurre en el lugar milésimas, donde el dígito 5 es el segundo número es mayor que el dígito 4 en el primer número en el mismo lugar. Debido a que 5 es mayor que 4, el segundo número es mayor que el primero. Es decir:

5.234 < 5.2357

Esta discusión sugiere el siguiente algoritmo.

Comparación de números decimales positivos

Agrega suficientes ceros finales para que ambos números tengan el mismo número de decimales.
Compara los dígitos en cada lugar, moviéndote de izquierda a derecha.
Tan pronto como encuentres dos dígitos en el mismo lugar que sean diferentes, el número decimal con el mayor dígito en este lugar es el número mayor.

Ejemplo 11

Compara 4.25 y 4.227.

Solución

Agregue un cero final al primer número decimal y alinee los números de la siguiente manera.

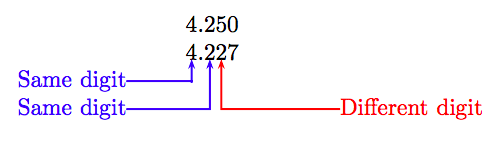
$Screen Shot 2019-09-09 at 2.38.23 PM.png$

La primera diferencia está en el lugar centésimas, donde el dígito 5 en el primer número es mayor que el dígito 2 en el mismo lugar del segundo número. De ahí que el primer número sea mayor que el segundo; es decir:

4.25 > 4.227

Ejercicio

Compara 8.34 y 8.348.

Contestar: 8.34 < 8.348

Al comparar números negativos, el número con la magnitud mayor es el número menor. De ahí que tengamos que ajustar nuestro algoritmo para comparar números decimales negativos.

Comparando números decimales negativos

Agrega suficientes ceros finales para que ambos números tengan el mismo número de decimales.
Compara los dígitos en cada lugar, moviéndote de izquierda a derecha.
Tan pronto como encuentres dos dígitos en el mismo lugar que sean diferentes, el número decimal con el mayor dígito en este lugar es el número menor.

Ejemplo 12

Compare −4.25 y −4.227.

Solución

Agregue un cero final al primer número decimal y alinee los números de la siguiente manera.

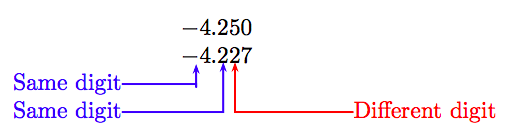
$Screen Shot 2019-09-09 at 2.38.30 PM.png$

La primera diferencia está en el lugar centésimas, donde el dígito 5 en el primer número es mayor que el dígito 2 en el mismo lugar del segundo número. De ahí que el primer número sea menor que el segundo; es decir:

−4.25 < −4.227

Ejercicio

Compare −7.86 y −7.85.

Contestar: −7.86 < −7.85

Ejercicios

1. ¿Qué dígito está en la columna décimas del número 4,552.0908?

2. ¿Qué dígito está en la columna milésimas del número 7,881.6127?

3. ¿Qué dígito está en la columna décimas del número 4,408.2148?

4. ¿Qué dígito está en la columna décimas del número 9,279.0075?

5. ¿Qué dígito está en la columna de las diez milésimas del número 2,709.5097?

6. ¿Qué dígito está en la columna de centésimas del número 1,743.1634?

7. ¿Qué dígito está en la columna de centésimas del número 3,501.4456?

8. ¿Qué dígito está en la columna de las diez milésimas del número 9,214.3625?

9. ¿Qué dígito está en la columna de centésimas del número 5,705.2193?

10. ¿Qué dígito está en la columna de centésimas del número 7,135.2755?

11. ¿Qué dígito está en la columna décimas del número 8,129.3075?

12. ¿Qué dígito está en la columna milésimas del número 6,971.4289?

En los Ejercicios 13-20, escriba el número decimal dado en forma expandida.

13. 46.139

14. 68.392

15. 643.19

16. 815.64

17. 14.829

18. 45.913

19. 658.71

20. 619.38

En los Ejercicios 21-28, siga el procedimiento que se muestra en los Ejemplos 1 y 2 para escribir el número decimal en forma expandida, luego combinar la parte del número entero y sumar la parte fraccionaria sobre un denominador común.

21. 32.187

22. 35.491

23. 36.754

24. 89.357

25. 596.71

26. 754.23

27. 527.49

28. 496.15

En los Ejercicios 29-40, pronuncia el número decimal dado. Escribe tu respuesta en palabras.

29. 0.9837

30. 0.6879

31. 0.2653

32. 0.8934

33. 925.47

34. 974.35

35. 83.427

36. 32.759

37. 63.729

38. 85.327

39. 826.57

40. 384.72

En los Ejercicios 41-52, convierte el decimal dado a una fracción mixta. No simplifiques tu respuesta.

41. 98.1

42. 625.591

43. 781.7

44. 219.999

45. 915.239

46. 676.037

47. 560.453

48. 710.9

49. 414.939

50. 120.58

51. 446.73

52. 653.877

En Ejercicios 53-60, convierte el decimal dado a una fracción impropia. No simplifiques tu respuesta.

53. 8.7

54. 3.1

55. 5.47

56. 5.27

57. 2.133

58. 2.893

59. 3.9

60. 1.271

En Ejercicios 61-68, convierte el decimal dado a una fracción. Reduce tu respuesta a los términos más bajos.

61. 0.35

62. 0.38

63. 0.06

64. 0.84

65. 0.98

66. 0.88

67. 0.72

68. 0.78

69. Redondear 79.369 a la centésima más cercana.

70. Vuelta 54.797 a la centésima más cercana.

71. Vuelta 71.2427 a la milésima más cercana.

72. Circular 59.2125 a la milésima más cercana.

73. Vuelta 29.379 a la décima más cercana.

74. Vuelta 42.841 a la décima más cercana.

75. Vuelta 89.3033 a la milésima más cercana.

76. Vuelta 9.0052 a la milésima más cercana.

77. Vuelta 20.655 a la décima más cercana.

78. Vuelta 53.967 a la décima más cercana.

79. Vuelta 19.854 a la centésima más cercana.

80. Vuelta 49.397 a la centésima más cercana.

En los Ejercicios 81-92, determinar cuál de las dos afirmaciones dadas es verdadera.

81. 0.30387617 < 0.3036562 or 0.30387617 > 0.3036562

82. 8.5934 < 8.554 or 8.5934 > 8.554

83. −0.034 < −0.040493 or −0.034 > −0.040493

84. −0.081284 < −0.08118 or −0.081284 > −0.08118

85. −8.3527 < −8.36553 or −8.3527 > −8.36553

86. −0.00786 < −0.0051385 or −0.00786 > −0.0051385

87. 18.62192 < 18.6293549 or 18.62192 > 18.6293549

88. 514.873553 < 514.86374 or 514.873553 > 514.86374

89. 36.8298 < 36.8266595 or 36.8298 > 36.8266595

90. 0.000681 < 0.00043174 or 0.000681 > 0.00043174

91. −15.188392 < −15.187157 or −15.188392 > −15.187157

92. −0.049785 < −0.012916 or −0.049785 > −0.012916

93. Escribe el número decimal en palabras.

i) Un diamante azul de 7.03 quilates recientemente descubierto subastado en Sotheby's.

ii) El recién lanzado telescopio europeo Planck permanecerá en órbita 1.75 años midiendo la radiación del Big Bang.

iii) El sol compone 0.9985 de la masa en nuestro sistema solar.

iv) Las partículas de arcilla son pequeñas, solo 0.0001 pulgadas.

94. Velocidad de la luz. El índice de refracción para un material dado es un valor que representa el número de veces más lento que una onda de luz viaja en ese material en particular que viaja en el vacío del espacio.

i) Reordenar los materiales por su índice de refracción de menor a mayor.

ii) ¿Cuántas veces más lenta es una onda de luz en un diamante en comparación con un vacío?

Material	Índice de refracción
Diamante	2.417
Vacío	1.0000
Plexiglás	1.51
Aire	1.0003
Agua	1.333
Circón	1.923
Cristal Corona	1.52
Hielo	1.31

95. ¿Día más corto? Científicos del Laboratorio de Propulsión a Chorro de la NASA calcularon que el terremoto en Chile pudo haber acortado la duración de un día en la Tierra en 1.26 millonésimas de segundo.

i) Escribir ese número completamente como decimal.

ii) Las observaciones reales de la duración del día son exactas a cinco millonésimas de segundo. Escribe esta fracción como decimal.

iii) Comparar los dos decimales anteriores y determinar cuál es menor. ¿Crees que los científicos pueden observar y medir la desaceleración calculada de la tierra?

RESPUESTAS

1. 0

3. 2

5. 7

7. 4

9. 1

11. 3

13. $40 + 6 + 1 10 + \frac{3}{100} + \frac{9}{1000}$

15. $600 + 40 + 3 + \frac{1}{10} + \frac{9}{100}$

17. $10 + 4 + \frac{8}{10} + \frac{2}{100} + \frac{9}{1000}$

19. $600 + 50 + 8 + \frac{7}{10} + \frac{1}{100}$

21. $32 + \frac{187}{1000}$

23. $36 + \frac{754}{1000}$

25. $596 + \frac{71}{100}$

27. $527 + \frac{49}{100}$

29. nueve mil ochocientos treinta y siete diezmilésimas

31. dos mil seiscientos cincuenta y tres diezmilésimas

33. novecientos veinticinco cuarenta y siete centésimas

35. ochenta y tres cuatrocientos veintisiete milésimas

37. sesenta y tres setecientos veintinueve milésimas

39. ochocientos veintiséis cincuenta y siete centésimas

41. $98 \frac{1}{10}$

43. $781 \frac{7}{10}$

45. $915 \frac{239}{1000}$

47. $560 \frac{453}{1000}$

49. $414 \frac{939}{1000}$

51. $446 \frac{73}{100}$

53. $\frac{87}{10}$

55. $\frac{547}{100}$

57. $\frac{2133}{1000}$

59. \ (\ frac {39} {10} |)

61. $\frac{7}{20}$

63. $\frac{3}{50}$

65. \ (\ frac {49} {50} |)

67. $\frac{18}{25}$

69. 79.37

71. 71.243

73. 29.4

75. 89.303

77. 20.7

79. 19.85

81. 0.30387617 > 0.3036562

83. −0.034 > −0.040493

85. −8.3527 > −8.36553

87. 18.62192 < 18.6293549

89. 36.8298 > 36.8266595

91. −15.188392 < −15.187157

93.

i) siete y tres centésimas

ii) una y setenta y cinco centésimas

iii) nueve mil novecientos ochenta y cinco diezmilésimas

iv) una décima milésima de pulgada

95.

i) 0.00000126

ii) 0.000005

iii) 0.00000126 < 0.000005; los científicos no podrían medir el cambio calculado en la duración de un día.

Search

Text Color

Text Size

Margin Size

Font Type