5.5: Dividir decimales

Última actualización
Guardar como PDF

Page ID: 113421

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

En esta y siguientes secciones hacemos uso de los términos divisor, dividendo, cociente y resto.

Divisor, dividendo, cociente y resto

Este esquema recuerda a los lectores la posición de estos términos en el proceso de división.

$Captura de pantalla 2019-09-11 al 1.05.57 PM.png$

Ahora que se definen estos términos, comenzamos la discusión de división de números decimales. Supongamos que deseamos dividir 637 por 100. Podríamos hacer esto en forma de fracción, cambiar el resultado a una fracción mixta, luego la fracción mixta a forma decimal.

\[\frac{637}{100} = 6 \frac{37}{100} = 6.37\nonumber \]

También podemos arreglar la división tanto como lo haríamos la división de dos números enteros.

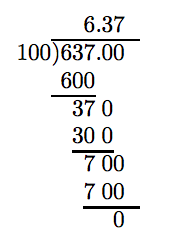
$Captura de pantalla 2019-09-11 en 1.10.16 PM.png$

Tenga en cuenta que sumar dos ceros después del punto decimal en el dividendo no cambia el valor de 637. Además, tenga en cuenta que procedemos como si estuviéramos dividiendo dos números enteros, colocando el punto decimal en el cociente directamente por encima del punto decimal en el dividendo.

Estas observaciones conducen al siguiente algoritmo.

Dividir un decimal por un número entero

Para dividir un número decimal por un número entero, proceda de la siguiente manera:

Establece la división larga como lo harías con la división de dos números enteros.
Realizar la división como si los números fueran ambos números enteros, sumando ceros a la derecha del punto decimal en el dividendo según sea necesario para completar la división.
Coloque el punto decimal en el cociente inmediatamente por encima del punto decimal en el dividendo.

Ejemplo 1

Divide 23 por 20.

Solución

Organizar como si usara división larga para dividir números enteros, agregando suficientes ceros a la derecha del punto decimal en el dividendo para completar la división.

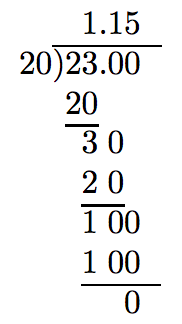
$Captura de pantalla 2019-09-11 en 1.13.53 PM.png$

De ahí que 23 dividido por 20 sea 1.15.

Adición de ceros a la derecha del punto decimal

Por lo general, no se ve de inmediato cuántos ceros a la derecha del punto decimal en el dividendo se necesitan. Estos ceros suelen agregarse en cada paso de la división, hasta que se complete la división o el usuario esté dispuesto a terminar el proceso y aceptar solo una estimación del cociente.

Ejemplo 2

Divida: 155.2 ÷ 25.

Solución

Organizar como si usara división larga para dividir números enteros, y comenzar.

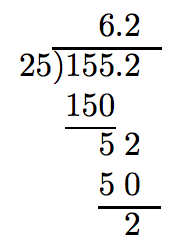
$Captura de pantalla 2019-09-11 en 1.14.00 PM.png$

Todavía tenemos un resto distinto de cero. Agregar otro cero no sirve de nada.

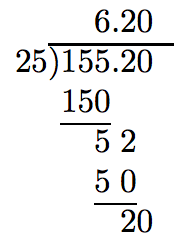
$Captura de pantalla 2019-09-11 en 1.14.05 PM.png$

No obstante, si sumamos un cero adicional más, la división se completa con un resto cero.

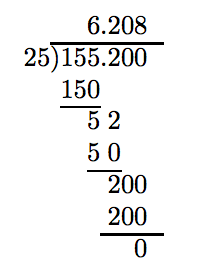
$Captura de pantalla 2019-09-11 en 1.17.55 PM.png$

Así, 155.2 dividido por 25 es 6.208.

Ejercicio

Divida: 42.55 ÷ 23

Contestar: 1.85

Divisores decimales Cuando el divisor contiene un punto decimal, tenemos un poco de trabajo que hacer antes de comenzar el proceso de división. Supongamos que deseamos dividir 1.25 por 2.5. En forma de fracción, podríamos comenzar con

\[ \frac{1.25}{2.5},\nonumber \]

luego despeja los decimales del denominador multiplicando tanto el numerador como el denominador por 10. Nota: Recordemos que multiplicando por 10 mueve el punto decimal un lugar a la derecha.

\[ \begin{aligned} \frac{1.25}{2.5} = \frac{1.25 \cdot 10}{2.5 \cdot 10} \\ = \frac{12.5}{25} \end{aligned}\nonumber \]

Así, dividir 1.25 por 2.5 equivale a dividir 12.5 por 25. Esto lo sabemos hacer.

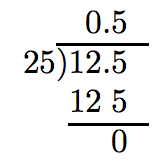
$Captura de pantalla 2019-09-11 en 1.22.03 PM.png$

Así, 1.25 dividido por 2.5 es 0.5.

Redacción Matemáticas

Nunca escribas .5. Siempre agregue el cero inicial en el lugar unos y escriba 0.5.

En lugar de trabajar en forma de fracción, podemos encargarnos de posicionar el punto decimal en el marco de división larga. Comience con:

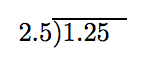
$Captura de pantalla 2019-09-11 en 1.23.54 PM.png$

Mueve el punto decimal en el divisor hasta el final del divisor, luego mueve el punto decimal en el dividendo un número igual de lugares.

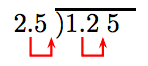
$Captura de pantalla 2019-09-11 en 1.23.57 PM.png$

Así, la división se convierte en

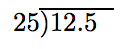
$Captura de pantalla 2019-09-11 en 1.24.03 PM.png$

y procedemos como arriba para encontrar el cociente. Esta discusión motiva el siguiente algoritmo.

Dividir por un divisor decimal

Si el divisor contiene un decimal, proceda de la siguiente manera:

Mueve el decimal hasta el final del divisor.
Mueve el decimal en el dividendo un número igual de lugares.

Entonces podemos completar la división usando las reglas para dividir un decimal por un número entero.

Ejemplo 3

Dividir:$\overline{ )4.392}$

Solución

Mueve el decimal en el divisor hasta el final del divisor. Mueve el decimal en el dividendo un número igual de lugares (dos lugares) a la derecha.

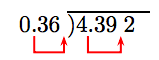
$Captura de pantalla 2019-09-11 en 1.30.09 PM.png$

Ahora podemos seguir el algoritmo para dividir un número decimal por un número entero.

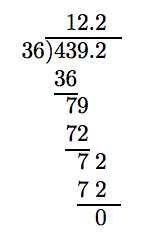
$Captura de pantalla 2019-09-11 en 1.30.15 PM.png$

Así, 4.392 dividido por 0.36 es 12.2.

Ejercicio

Dividir:$0.45 \overline{)36.99}$

Contestar: 82.2

Dividir números decimales firmados

Las reglas que rigen la división de los números decimales firmados son idénticas a las reglas que rigen la división de enteros.

Como Signos. El cociente de dos números decimales con signos similares es positivo. Es decir:

\[\frac{(+)}{(+)} = + \text{ and } \frac{(−)}{(−)} = +\nonumber \]

A diferencia de Signos. El cociente de dos números decimales con signos diferentes es negativo. Es decir:

\[\frac{(+)}{(−)} = − \text{ and } \frac{(−)}{(+)} = −\nonumber \]

Ejemplo 4

Dividir: −0.03 ÷ 0.024.

Solución

Primero, divide las magnitudes. Mueve el decimal en el divisor hasta el final del divisor. Mueve el decimal en el dividendo un número igual de lugares (tres lugares) a la derecha. Tenga en cuenta que esto requiere un cero final adicional en el dividendo.

$Captura de pantalla 2019-09-11 en 1.46.22 PM.png$

Nuestro problema entonces se convierte en:

\ [24\ overline {24) 30}\)

Ahora podemos seguir el algoritmo para dividir un número decimal por un número entero. Tenga en cuenta que tenemos que sumar dos ceros finales en el dividendo para completar la división con un resto cero.

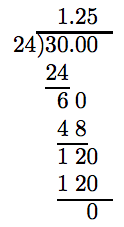
$Captura de pantalla 2019-09-11 en 1.46.30 PM.png$

Finalmente, debido a que el cociente de signos contrarios es negativo, −0.03 dividido por 0.024 es −1.25. Es decir,

\[ \frac{-0.03}{0.024} = -1.25.\nonumber \]

Ejercicio

Dividir: −0.0113 ÷ 0.05

Contestar: −0.226

Redondeo

A veces no se necesita una representación decimal exacta de una fracción y es que una aproximación es más que adecuada.

Ejemplo 5

Convierte 4/7 a decimal. Redondea tu respuesta a la centésima más cercana.

Solución

Tenemos que llevar la división un lugar más allá del lugar centésimas.

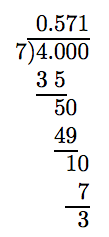
$Captura de pantalla 2019-09-11 en 1.50.40 PM.png$

Para redondear a la centésima más cercana, primero identifique los dígitos de redondeo y pruebe.

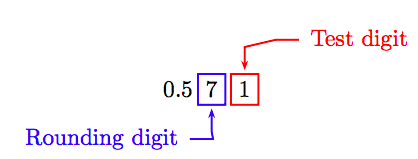
$Captura de pantalla 2019-09-11 en 1.50.45 PM.png$

Debido a que el “dígito de prueba” es menor 5, deje solo el dígito de redondeo y trunca. Por lo tanto, corregir a la centésima más cercana, 4/7 ≈ 0.57.

Ejercicio

Convierte 5/7 a decimal. Redondea tu respuesta a la centésima más cercana.

Contestar: 0.71

Dividiendo por poderes de diez

Recordar:

\[\begin{aligned} 10^1 = 10 \\ 10^2 = 10 \cdot 10 = 100 \\ 10^3 = 10 \cdot 10 \cdot 10 = 1000 \end{aligned}\nonumber \]

Poderes de Diez

En la expresión 10 n, el exponente coincide con el número de ceros en la respuesta. De ahí que 10 n será un 1 seguido de n ceros.

Así, 10 ⁴ = 10, 000, 10 ⁵ = 100, 000, etc. El exponente nos dice cuántos ceros seguirán al 1.

Dividamos 123456.7 por 1000.

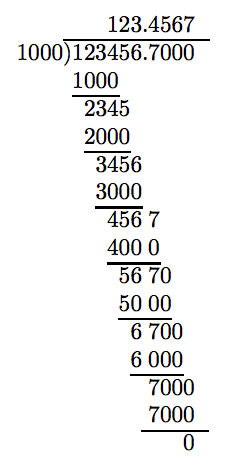
$Captura de pantalla 2019-09-11 en 1.56.26 PM.png$

Tenga en cuenta el resultado: 123456.7 dividido por 1000 es 123.4567. ¡Dividiendo por 1000 mueve el punto decimal 3 lugares a la izquierda!

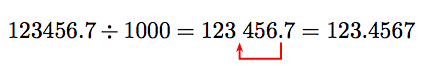
$Captura de pantalla 2019-09-11 en 1.56.32 PM.png$

Esta discusión lleva al siguiente resultado.

Dividir un decimal por una potencia de diez

Dividiendo un número decimal por 10 n moverá el punto decimal n lugares hacia la izquierda.

Ejemplo 6

Simplificar: 123456.7 ÷ 10 ⁴

Solución

Dividiendo por 10 ⁴ (o equivalentemente, 10,000) mueve el punto decimal cuatro lugares hacia la izquierda. Así, 123456.7 ÷ 10 ⁴ = 12.34567.

Ejercicio

Simplificar: 123456.7 ÷ 10 ²

Contestar: 1234.567

Orden de Operaciones

Recordamos a los lectores las Reglas Guía Orden de Operación s.

Reglas que guían el orden de operaciones

Al evaluar expresiones, proceda en el siguiente orden.

Evalúe primero las expresiones contenidas en los símbolos de agrupación. Si los símbolos de agrupación están anidados, evalúe primero la expresión en el par más interno de símbolos de agrupación.
Evaluar todos los exponentes que aparecen en la expresión.
Realizar todas las multiplicaciones y divisiones en el orden en que aparezcan en la expresión, moviéndose de izquierda a derecha.
Realizar todas las sumas y restaciones en el orden en que aparezcan en la expresión, moviéndose de izquierda a derecha.

Además, cuando las fracciones están presentes:

Expresiones fraccionarias

Si una expresión fraccionaria está presente, simplifique el numerador y el denominador por separado, luego divida.

Ejemplo 7

Evaluar ab/ (c + d), dado que a = 2.1, b = −3.4, c = −1.3, y d = 1.1.

Solución

Recordemos que es una buena práctica preparar una expresión para sustitución mediante el uso de paréntesis.

\[ab/(c + d) = (~)(~)/((~) +(~)) \nonumber \]

Sustituya los valores dados por a, b, c y d, luego use el Orden de Operaciones Rector de Reglas para simplificar la expresión resultante.

\[ \begin{aligned} ab/(c+d) = (2.1)(-3.4)/((-1.3)+(1.1)) ~ & \textcolor{red}{2.1, -3.4,-1.3, 1.1 \text{ for } a, b, c, d.} \\ = (2.1)(-3.4)/(-0.2) ~ & \textcolor{red}{ \text{ Parens: } (-1.3) + (1.1) = -0.2.} \\ =-7.14/(-0.2) ~ & \textcolor{red}{ \text{ Multiply: } (2.1)(-3.4) = -7.14.} \\ =35.7 ~ & \textcolor{red}{ \text{ Divide: } -7.14/(-0.2) = 35.7} \end{aligned}\nonumber \]

Ejercicio

Si a = −2.1, b = 1.7, c = 4 y d = 0.05, evalúe:

\[\frac{a+b}{cd}\nonumber \]

Contestar: −2

Ejemplo 8

Dado a = 0.1 y b = −0.3, evaluar la expresión

\[\frac{a+2b}{2a+b}.\nonumber \]

Solución

Sustituya los valores dados, luego use el Orden de Operaciones Rector de Reglas para simplificar la expresión resultante.

\[ \begin{aligned} \frac{a+2b}{2a+b} = \frac{(0.1)+2(-0.3)}{2(0.1)+(-0.3)} ~ & \textcolor{red}{ \text{ 0.1 for } a,~ -0.3 \text{ for } b.} \end{aligned}\nonumber \]

Simplifica el numerador, simplifica el denominador, luego divide.

\[ \begin{aligned} = \frac{0.1+(-0.6)}{0.2+(-0.3)} ~ & \textcolor{red}{ \begin{aligned} \text{ Numerator: } 2(-0.3) = -0.6. \\ \text{ Denominator: } 2(0.1)=0.2. \end{aligned}} \\ = \frac{-0.5}{-0.1} ~ & \textcolor{red}{ \begin{aligned} \text{ Numerator: } 0.1 + (-0.6)=-0.5 \\ \text{ Denominator: } 0.2 + (-0.3) = -0.1. \end{aligned}} \\ =5 ~ & \textcolor{red}{ \text{ Divide: } -0.5/(-0.1)=5.} \end{aligned}\nonumber \]

Ejercicio

Si a = 0.5 y b = −0.125, evalúe:

\[ \frac{2a-b}{a+2b}\nonumber \]

Contestar: 4.5

Ejercicios

En Ejercicios 1-16, divide los números.

1. $\frac{39}{52}$

2. $\frac{16}{25}$

3. $\frac{755.3}{83}$

4. $\frac{410.4}{76}$

5. $\frac{333}{74}$

6. $\frac{117}{65}$

7. $\frac{32.12}{73}$

8. $\frac{12.32}{44}$

9. $\frac{37.63}{71}$

10. $\frac{20.46}{31}$

11. $\frac{138}{92}$

12. $\frac{110}{25}$

13. $\frac{17}{25}$

14. $\frac{18}{75}$

15. $\frac{229.5}{51}$

16. $\frac{525.6}{72}$

En Ejercicios 17-40, divide los decimales.

17. $\frac{0.3478}{0.47}$

18. $\frac{0.4559}{0.97}$

19. $\frac{1.694}{2.2}$

20. $\frac{1.008}{1.8}$

21. $\frac{43.61}{4.9}$

22. $\frac{22.78}{3.4}$

23. $\frac{1.107}{0.41}$

24. $\frac{2.465}{0.29}$

25. $\frac{2.958}{0.51}$

26. $\frac{5.141}{0.53}$

27. $\frac{71.76}{7.8}$

28. $\frac{14.08}{8.8}$

29. $\frac{0.8649}{0.93}$

30. $\frac{0.3901}{0.83}$

31. $\frac{0.6958}{0.71}$

32. $\frac{0.1829}{0.31}$

33. $\frac{1.248}{0.52}$

34. $\frac{6.375}{0.85}$

35. $\frac{62.56}{9.2}$

36. $\frac{28.08}{7.8}$

37. $\frac{6.278}{8.6}$

38. $\frac{3.185}{4.9}$

39. $\frac{2.698}{7.1}$

40. $\frac{4.959}{8.7}$

En los Ejercicios 41-64, divide los decimales.

41. $\frac{−11.04}{1.6}$

42. $\frac{−31.27}{5.3}$

43. $\frac{−3.024}{5.6}$

44. $\frac{−3.498}{5.3}$

45. $\frac{−0.1056}{0.22}$

46. $\frac{−0.2952}{−0.72}$

47. $\frac{0.3204}{−0.89}$

48. $\frac{0.3306}{−0.38}$

49. $\frac{−1.419}{0.43}$

50. $\frac{−1.625}{−0.25}$

51. $\frac{−16.72}{−2.2}$

52. $\frac{−66.24}{9.2}$

53. $\frac{−2.088}{−0.87}$

54. $\frac{−2.025}{−0.75}$

55. $\frac{−1.634}{−8.6}$

56. $\frac{−3.094}{3.4}$

57. $\frac{−0.119}{0.85}$

58. $\frac{0.5766}{−0.62}$

59. $\frac{−3.591}{−6.3}$

60. $\frac{−3.016}{5.8}$

61. $\frac{36.96}{−4.4}$

62. $\frac{−78.26}{−8.6}$

63. $\frac{−2.156}{−0.98}$

64. $\frac{−6.072}{0.66}$

En los Ejercicios 65-76, divide el decimal por la potencia dada de 10.

65. $\frac{524.35}{100}$

66. $\frac{849.39}{100}$

67. $\frac{563.94}{10^3}$

68. $\frac{884.15}{10^3}$

69. $\frac{116.81}{10^2}$

70. $\frac{578.01}{10^3}$

71. $\frac{694.55}{10}$

72. $\frac{578.68}{100}$

73. $\frac{341.16}{10^3}$

74. $\frac{46.63}{10^4}$

75. $\frac{113.02}{1000}$

76. $\frac{520.77}{1000}$

77. Calcula el cociente 52/83, y redondea tu respuesta a la décima más cercana.

78. Calcula el cociente 43/82 y redondea tu respuesta al décimo más cercano.

79. Calcula el cociente 51/59 y redondea tu respuesta al décimo más cercano.

80. Calcula el cociente 17/69, y redondea tu respuesta a la décima más cercana.

81. Calcula el cociente 5/74 y redondea tu respuesta a la centésima más cercana.

82. Calcula el cociente 3/41, y redondea tu respuesta a la centésima más cercana.

83. Calcula el cociente 5/94 y redondea tu respuesta a la centésima más cercana.

84. Calcula el cociente 3/75 y redondea tu respuesta a la centésima más cercana.

85. Calcula el cociente 7/72 y redondea tu respuesta a la centésima más cercana.

86. Calcula el cociente 4/57, y redondea tu respuesta a la centésima más cercana.

87. Calcula el cociente 16/86 y redondea tu respuesta al décimo más cercano.

88. Calcula el cociente 21/38, y redondea tu respuesta a la décima más cercana.

En los Ejercicios 89-100, simplificar la expresión dada.

89. $\frac{7.5 \cdot 7.1 − 19.5}{0.54}$

90. $\frac{1.5(−8.8) − (−18.6)}{1.8}$

91. $\frac{17.76 − (−11.7)}{0.52}$

92. $\frac{−14.8 − 2.1}{2.62}$

93. $\frac{−18.22 − 6.7}{14.75 − 7.75}$

94. $\frac{1.4 − 13.25}{−6.84 − (−2.1)}$

95. $\frac{−12.9 − (−10.98)}{0.5^2}$

96. $\frac{5.1 − (−16.5)}{(−1.5)^2}$

97. $\frac{−9.5 \cdot 1.6 − 3.7}{−3.6}$

98. $\frac{6.5(−1.6) − 3.35}{−2.75}$

99. $\frac{−14.98 − 9.6}{17.99 − 19.99}$

100. $\frac{−5.6 − 7.5}{−5.05 − 1.5}$

101. Dado a = −2.21, c = 3.3, y d = 0.5, evaluar y simplificar la siguiente expresión.

\[\frac{a − c}{d^2}\nonumber \]

102. Dado a = 2.8, c = −14.68, y d = 0.5, evaluar y simplificar la siguiente expresión.

\[\frac{a − c}{d^2}\nonumber \]

103. Dado a = −5.8, b = 10.37, c = 4.8 y d = 5.64, evalúe y simplifique la siguiente expresión:

\[\frac{a − b}{c − d}\nonumber \]

104. Dado a = −10.79, b = 3.94, c = −3.2 y d = −8.11, evalúe y simplifique la siguiente expresión:

\[\frac{a − b}{c − d}\nonumber \]

105. Dado a = −1.5, b = 4.7, c = 18.8 y d = −11.75, evalúe y simplifique la siguiente expresión.

\[\frac{ab − c}{d}\nonumber \]

106. Dado a = 9.3, b = 6.6, c = 14.27, y d = 0.2, evaluar y simplificar la siguiente expresión.

\[\frac{ab − c}{d}\nonumber \]

107. Plantas de biodiesel. Hay alrededor de 180 plantas de biodiesel operando en unos 40 estados. De los estados que los tienen, ¿cuál es el promedio de plantas de biodiesel por estado? Associated Press-Times-Standard 01/02/10 La incipiente industria de biocombustibles termina el año con una nota dura.

108. Hongo de murciélago. Un hongo llamado “síndrome de nariz blanca” ha matado a aproximadamente 500,000 murciélagos en todo el país. Esto significa que no se comen alrededor de 2,400,000 libras de insectos a lo largo del año, dice la bióloga del Servicio Forestal Becky Ewing. ¿Cuántas libras de insectos come anualmente un murciélago promedio? Associated Prensa-Times-Estándar 5/2/09

109. Retraso de patentes. En la Oficina de Patentes y Marcas de Estados Unidos, 6000 examinadores tienen una acumulación de 770,000 nuevas solicitudes de patentes no examinadas. ¿Cuántas solicitudes es esa para que cada examinador se ponga al día? Redondea tu respuesta a la décima más cercana. Associated Prensa-Times-Estándar 5/5/09

110. Hacerlo bien. La gran aseguradora de salud Wellpoint, Inc., propietaria de Anthem Blue Cross, ganó 536 millones de dólares en los últimos tres meses de 2009. ¿Cuál fue el promedio de ganancias mensuales para la aseguradora durante ese periodo? Redondear al millón más cercano. Associated Press-Times-Standard 02/09/10 El secretario del HHS pide a Anthem Blue Cross que justifique el alza de tasas.

111. Ciberataques. El Pentágono ha gastado 100 millones de dólares en un período de seis meses respondiendo y reparando daños causados por ciberataques y otros problemas de redes informáticas. ¿Cuál es la cantidad promedio de dinero gastado por mes durante ese tiempo? Redondea tu respuesta a la centésima de millón más cercana. Associated Prensa-Times-Estándar 4/19/09

112. Leche diaria. La vaca promedio de California puede producir 2,305 galones de leche anualmente. ¿Cuánta leche puede producir una vaca cada día? Redondea tu respuesta a la centésima de galón más cercana. www.moomilk.com/faq.htm

113. Correo de medios. Para promocionar su negocio, Theresa envía varios paquetes vía Media Mail. Un paquete que pesa 2 lbs. cuesta $2.77, otro paquete que pesa 3 lbs. cuesta $3.16, y el tercer paquete que pesa 5 lbs. cuesta $3.94 para enviar por correo. ¿Cuál fue el costo promedio por libra para enviar los paquetes por correo? Redondea tu resultado al centavo más cercano. www.usps.com/prices/media-mailprices.htm

RESPUESTAS

1. 0.75

3. 9.1

5. 4.5

7. 0.44

9. 0.53

11. 1.5

13. 0.68

15. 4.5

17. 0.74

19. 0.77

21. 8.9

23. 2.7

25. 5.8

27. 9.2

29. 0.93

31. 0.98

33. 2.4

35. 6.8

37. 0.73

39. 0.38

41. −6.9

43. −0.54

45. −0.48

47. −0.36

49. −3.3

51. 7.6

53. 2.4

55. 0.19

57. −0.14

59. 0.57

61. −8.4

63. 2.2

65. 5.2435

67. 0.56394

69. 1.1681

71. 69.455

73. 0.34116

75. 0.11302

77. 0.6

79. 0.9

81. 0.07

83. 0.05

85. 0.10

87. 0.2

89. 62.5

91. 117.84

93. −3.56

95. −7.68

97. 5.25

99. 12.29

101. −22.04

103. 19.25

105. 2.2

107. 4.5 plantas de biodiesel

109. 128.3

111. $16.67 millones

113. $0.99 por libra

Search

Text Color

Text Size

Margin Size

Font Type