7.2: Porcentaje, Decimales, Fracciones
- Page ID
- 113427
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)En el cuadrado que se muestra en la Figura\(\PageIndex{1}\), se ha dividido un cuadrado grande en diez filas de diez cuadraditos en cada fila. En la Figura 7.1, hemos sombreado 20 de 100 posibles cuadraditos, o 20% del número total de cuadraditos pequeños.
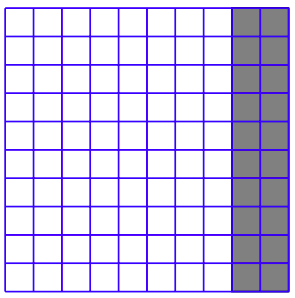
El significado del porcentaje
Por ciento significa “partes por cien”.
En la Figura 7.1, 80 de un posible 100 cuadrados se dejan sin sombra. Así, el 80% de los cuadraditos están sin sombra. Si en cambio sombreamos 35 de los 100 cuadrados, entonces el 35% de los cuadraditos estarían sombreados. Si sombreamos todos los cuadraditos, entonces el 100% de los cuadraditos estarían sombreados (100 de 100).
Entonces, cuando escuche la palabra “por ciento”, piense “partes por cien”.
Cambio de un Porcentaje a una Fracción
Con base en la discusión anterior, es bastante sencillo cambiar un porcentaje a una fracción.
Porcentaje a Fracción
Para cambiar un porcentaje a una fracción, baja el signo de porcentaje y poner el número por encima del 100.
Ejemplo 1
Cambiar 24% a una fracción.
Solución
Deja caer el símbolo de porcentaje y pon 24 sobre 100.
\[ \begin{aligned} 24 \% = \frac{24}{100} ~ & \textcolor{red}{ \text{ Percent: Parts per hundred.}} \\ = \frac{6}{25} ~ & \textcolor{red}{ \text{ Reduce.}} \end{aligned}\nonumber \]
De ahí que 24% = 6/25.
Ejercicio
Cambiar 36% a una fracción reducida a términos más bajos.
- Contestar
-
9/25
Ejemplo 2
Cambiar\(14 \frac{2}{7} \%\) a una fracción.
Solución
Deja caer el símbolo de porcentaje y pon\(14 \frac{2}{7}\) más de 100.
\[ \begin{aligned} 14 \frac{2}{7} \% = \frac{14 \frac{2}{7}}{100} ~ & \textcolor{red}{ \text{ Percent: Parts per hundred.}} \\ = \frac{\frac{100}{7}}{100} ~ & \textcolor{red}{ \text{ Mixed to improper fraction.}} \\ = \frac{100}{7} \cdot \frac{1}{100} ~ & \textcolor{red}{ \text{ Invert and multiply.}} \\ = \frac{\cancel{100}}{7} \cdot \frac{1}{\cancel{100}} ~ & \textcolor{red}{ \text{ Cancel.}} \\ = \frac{1}{7} \end{aligned}\nonumber \]
Por lo tanto,\(14 \frac{2}{7} \%=1/7.\)
Ejercicio
Cambiar\(11 \frac{1}{9} \%\) a una fracción reducida a términos más bajos.
- Contestar
-
1/9
Ejemplo 3
Cambiar 28.4% a una fracción.
Solución
Deja caer el símbolo porcentual y pon 28.4 sobre 100.
\[ \begin{aligned} 28.4 \% = \frac{28.4}{100} ~ & \textcolor{red}{ \text{ Percent: Parts per hundred.}} \\ = \frac{28.4 \cdot \textcolor{red}{10}}{100 \cdot \textcolor{red}{10}} ~ & \textcolor{red}{ \text{ Multiply numerator and denominator by 10.}} \\ = \frac{284}{1000} ~ & \textcolor{red}{ \text{ Multiplying by 10 moves decimal point one place right.}} \\ = \frac{71 \cdot 4}{250 \cdot 4} ~ & \textcolor{red}{ \text{ Factor.}} \\ = \frac{71}{250} ~ & \textcolor{red}{ \text{ Cancel common factor.}} \end{aligned}\nonumber \]
Ejercicio
Cambiar 87.5% a una fracción reducida a términos más bajos.
- Contestar
-
7/8
Cambio de un Porcentaje a Decimal
Para cambiar un porcentaje a un decimal, sólo hay que recordar que por ciento significa “partes por cien”.
Ejemplo 4
Cambiar 23.25% a decimal.
Solución
Deja caer el símbolo de porcentaje y pon 23.25 sobre 100.
\[ \begin{aligned} 23.25 \% = \frac{23.25}{100} ~ & \textcolor{red}{ \text{ Percent: Parts per hundred.}} \\ = 0.2325 ~ & \textcolor{red}{ \text{ Dividing by 100 moves decimal point 2 places left.}} \end{aligned}\nonumber \]
Por lo tanto, 23.25% = 0.2325.
Ejercicio
Cambiar 2.4% a decimal.
- Contestar
-
0.024
Este último ejemplo motiva la siguiente regla simple.
Cambio de un Porcentaje a Decimal
Para cambiar un porcentaje a un decimal, baje el símbolo de porcentaje y mover el punto decimal dos lugares a la izquierda.
Ejemplo 5
Cambiar\(5 \frac{1}{2} \%\) a un decimal.
Solución
Tenga en cuenta que 1/2=0.5, luego mueva los decimales 2 lugares hacia la izquierda.
\[ \begin{aligned} 5 \frac{1}{2} \% = 5.5 \% ~ & \textcolor{red}{1/2 = 0.5.} \\ = 0.05 5 ~ & \textcolor{red}{ \begin{array}{l} \text{ Drop % symbol.} \\ \text{ Move decimal point 2 places left.} \end{array}} \\ = 0.055 \end{aligned}\nonumber \]
Por lo tanto,\(5 \frac{1}{2} \%=0.055\).
Ejercicio\(\PageIndex{1}\)
Cambiar\(6 \frac{3}{4} \%\) a un decimal.
- Contestar
-
0.0675
Cambio de un Decimal a un Porcentaje
Cambiar un decimal a un porcentaje es exactamente lo contrario de cambiar un porcentaje a un decimal. En este último caso, bajamos el símbolo de porcentaje y movemos el punto decimal 2 lugares hacia la izquierda. La siguiente regla hace justamente lo contrario.
Cambio de un Decimal a un Porcentaje
Para cambiar un decimal a un porcentaje, mueva el punto decimal dos lugares a la derecha y agregue un símbolo de porcentaje.
Ejemplo 6
Cambiar 0.0725 a un por ciento.
Solución
Mueva el punto decimal dos lugares a la derecha y agregue un símbolo de porcentaje.
\[ \begin{aligned} 0.0725 = 007.25 \% \\ = 7.25 \% \end{aligned}\nonumber \]
Ejercicio
Cambiar a 0.0375 a un por ciento.
- Contestar
-
3.75%
Ejemplo 7
Cambiar 1.025 a un por ciento.
Solución
Mueva el punto decimal dos lugares a la derecha y agregue un símbolo de porcentaje.
\[ \begin{aligned} 1.025 = 102.5 \% \\ = 102.5 \% \end{aligned}\nonumber \]
Ejercicio
Cambiar 0.525 a un por ciento.
- Contestar
-
52.5%
Cambio de una Fracción a un Porcentaje
Una forma de proceder es cambiar primero la fracción a un decimal, luego cambiar el decimal resultante a un porcentaje.
Fracciones a porcentajes: Técnica #1
Para cambiar una fracción a un porcentaje, siga estos pasos:
- Divide el numerador por el denominador para cambiar la fracción a un decimal.
- Mueva el punto decimal en el resultado dos lugares a la derecha y agregue un símbolo de porcentaje.
Ejemplo 8
Usa la Técnica #1 para cambiar 5/8 a un por ciento.
Solución
Cambie 5/8 a un decimal, luego cambie el decimal a un porcentaje.
Para cambiar 5/8 a un decimal, divida 5 por 8. Dado que el denominador es un producto de dos, el decimal debe terminar.
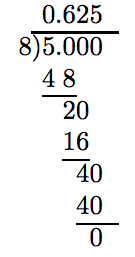
Para cambiar 0.625 a un porcentaje, mueva el punto decimal 2 lugares a la derecha y agregue un símbolo de porcentaje.
0.625 = 0 62.5% = 62.5%
Ejercicio
Cambiar 5/16 a un por ciento.
- Contestar
-
31.35%
Una segunda técnica es crear una fracción equivalente con un denominador de 100.
Fracciones a porcentajes: Técnica #2
Para cambiar una fracción a un porcentaje, cree una fracción equivalente con un denominador de 100.
Ejemplo 9
Usa la Técnica #2 para cambiar 5/8 a un por ciento.
Solución
Crea una fracción equivalente para 5/8 con un denominador de 100.
\[ \frac{5}{8} = \frac{x}{100}\nonumber \]
Resuelve esta proporción para x.
\[ \begin{aligned} 8x = 500 ~ & \textcolor{red}{ \text{ Cross multiply.}} \\ \frac{8x}{8} = \frac{500}{8} ~ & \textcolor{red}{ \text{ Divide both sides by 8.}} \\ x = \frac{125}{2} ~ & \textcolor{red}{ \text{ Reduce: Divide numerator and denominator by 4.}} \\ x = 62.5 ~ & \textcolor{red}{ \text{ Divide.}} \end{aligned}\nonumber \]
Por lo tanto,
\[ \frac{5}{8} = \frac{62.5}{100} = 62.5 \%.\nonumber \]
Finalización Alterna
También podríamos cambiar 125/2 a una fracción mixta; es decir, 125/2 = 62 1 2. Entonces,
\[ \frac{5}{8} = \frac{62 \frac{1}{2}}{100} = 62 \frac{1}{2} \%.\nonumber \]
Misma respuesta.
Ejercicio
Cambiar 4/9 a un por ciento.
- Contestar
-
\(44 \frac{4}{9} \%\)
A veces nos contentaremos con una aproximación.
Ejemplo 10
Cambiar 4/13 a un por ciento. Redondee su respuesta al décimo de un porcentaje más cercano.
Solución
Utilizaremos la Técnica #1.
Para cambiar 4/13 a un decimal, divida 4 por 13. Dado que el denominador tiene factores distintos a los 2's y 5's, el decimal se repetirá. No obstante, pretendemos redondear a la décima de porcentaje más cercana, por lo que llevaremos la división a cuatro decimales solamente. (Cuatro lugares son necesarios porque vamos a estar moviendo el punto decimal dos lugares a la derecha. )
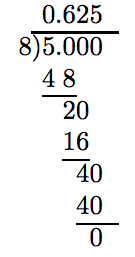
Para cambiar el decimal a un porcentaje, mueva el punto decimal dos lugares a la derecha.
0.3076 ≈ 0 30.76% ≈ 30.76%
Para redondear al décimo de porcentaje más cercano, identifique los dígitos de redondeo y pruebe.
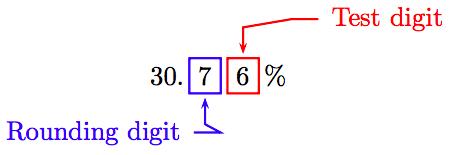
Debido a que el dígito de prueba es mayor o igual a 5, agregue 1 al dígito de redondeo y trunca. Por lo tanto,
0.03076 ≈ 30.8%.
Ejercicio
Cambiar 4/17 a un por ciento. Redondee su respuesta al décimo de un porcentaje más cercano.
- Contestar
-
23.5%
Ejercicios
En Ejercicios 1-18, convertir el porcentaje dado a una fracción, y simplificar el resultado.
1. \(4 \frac{7}{10} \%\)
2. \(7 \frac{1}{4} \%\)
3. \(7 \frac{2}{9} \%\)
4. \(4 \frac{9}{10} \%\)
5. 11.76%
6. 15.2%
7. 13.99%
8. 18.66%
9. \(4 \frac{1}{2} \%\)
10. \(8 \frac{5}{8} \%\)
11. 192%
12. 5%
13. 86%
14. 177%
15. 130%
16. 80%
17. 4.07%
18. 6.5%
En Ejercicios 19-34, convertir el porcentaje dado a un decimal.
19. 124%
20. 4%
21. 0.6379%
22. 0.21%
23. 28%
24. 5.4%
25. 0.83%
26. 0.3344%
27. 8%
28. 3%
29. 59.84%
30. 0.17%
31. 155%
32. 7%
33. 36.5%
34. 39.7%
En Ejercicios 35-50, convertir el decimal dado a un porcentaje.
35. 8.888
36. 5.1
37. 0.85
38. 0.08
39. 1.681
40. 3.372
41. 0.14
42. 4.89
43. 8.7
44. 8.78
45. 0.38
46. 1.67
47. 0.02
48. 0.07
49. 0.044
50. 0.29
En los Ejercicios 51-68, convertir la fracción dada a un porcentaje.
51. \(\frac{1}{2}\)
52. \(\frac{29}{8}\)
53. \(\frac{5}{2}\)
54. \(\frac{4}{5}\)
55. \(\frac{8}{5}\)
56. \(\frac{7}{20}\)
57. \(\frac{14}{5}\)
58. \(\frac{3}{2}\)
59. \(\frac{9}{2}\)
60. \ (\ frac {18} {25} |)
61. \(\frac{9}{4}\)
62. \(\frac{7}{8}\)
63. \(\frac{7}{5}\)
64. \(\frac{4}{25}\)
65. \(\frac{6}{5}\)
66. \(\frac{23}{8}\)
67. \(\frac{12}{5}\)
68. \(\frac{13}{2}\)
69. Convierte 24/29 a un por ciento, y redondear tu respuesta a la centésima de por ciento más cercana.
70. Convierte 5/3 a un por ciento, y redondear tu respuesta a la centésima de por ciento más cercana.
71. Convierte 15/7 a un por ciento, y redondear tu respuesta a la décima más cercana de un por ciento.
72. Convierte 10/7 a un por ciento, y redondear tu respuesta a la décima más cercana de un por ciento.
73. Convierte 7/24 a un por ciento, y redondear tu respuesta a la centésima de por ciento más cercana.
74. Convierte 5/6 a un por ciento, y redondear tu respuesta a la centésima de por ciento más cercana.
75. Convierte 8/3 a un por ciento, y redondear tu respuesta a la décima más cercana de un por ciento.
76. Convierte 22/21 a un por ciento, y redondear tu respuesta a la décima de por ciento más cercana.
77. Convierte 9/23 a un por ciento, y redondear tu respuesta a la décima más cercana de un por ciento.
78. Convierte 11/9 a un por ciento, y redondear tu respuesta a la décima más cercana de un por ciento.
79. Convierte 17/27 a un por ciento, y redondear tu respuesta a la centésima de por ciento más cercana.
80. Convierte 22/27 a un por ciento, y redondear tu respuesta a la centésima de por ciento más cercana.
81. Tasas delictivas. A continuación se muestran las tasas preliminares de delincuencia para los primeros seis meses de 2009 en comparación con el mismo periodo de 2008. Associated Press-Times-Standard 12/22/09 A pesar de la recesión, los índices delictivos nacionales siguen bajando.
\[ \begin{array}{c c} \text{Murder } & ~ −10.0 \% \\ \text{Forcible rape } & ~ −3.3 \% \\ \text{Robbery } & ~ −6.5 \% \\ \text{Aggravated assault } & ~ −3.2 \% \\ \text{Burglary } ~ & −2.5 \% \\ \text{Larceny-theft } & ~ −5.3 \% \\ \text{Motor vehicle theft } & ~ −18.75 \% \\ \text{Arson } & ~ −8.2 \% \end{array}\nonumber \]
Fuente: Oficina Federal de Investigaciones
i) ¿Qué indican los signos negativos?
ii) ¿Qué tipo de delito disminuyó más?
iii) ¿Qué tipo de delito disminuyó menos?
82. Huracanes Mayores. 5 de los 8 huracanes en 2008 fueron categorizados como mayores. Escriba el número fraccional de huracanes mayores en 2008 como porcentaje. NOAA Prensa Asociada 5/22/09
83. Posibilidad de inundación. Estos extractos son de la historia Cuerpo: La obra de la presa disminuye la posibilidad de inundación en el área de Seattle publicada en el Times-Standard el 6 de noviembre de 2009. Escribe las cuatro probabilidades de inundación como porcentaje de probabilidad. Redondear a la décima de porcentaje más cercana si es necesario.
i) El coronel Anthony Wright, del Cuerpo de Ingenieros del Ejército de Estados Unidos, hablando de las reparaciones a la presa Green River, informó que ahora había una posibilidad de 1 en 25 de que una tormenta obligara a los cuerpos a liberar suficiente agua del embalse de la presa para provocar una inundación río abajo en el Valle del Río Verde.
ii) Las probabilidades de inundaciones generalizadas en el valle mejoran a 1 de cada 32 cuando se tienen en cuenta todos los esfuerzos de sacos de arena y protección contra inundaciones.
iii) Anteriormente, el Cuerpo de Ingenieros dijo que la posibilidad de inundaciones generalizadas era de 1 en 4.
iv) Cuando la presa opera a su capacidad, existe una probabilidad de inundación de 1 en 140.
RESPUESTAS
1. \(\frac{47}{1000}\)
3. \(\frac{13}{180}\)
5. \(\frac{147}{1250}\)
7. \(\frac{1399}{10000}\)
9. \(\frac{9}{200}\)
11. \(\frac{48}{25}\)
13. \(\frac{43}{50}\)
15. \(\frac{13}{10}\)
17. \(\frac{407}{10000}\)
19. 1.24
21. 0.006379
23. 0.28
25. 0.0083
27. 0.08
29. 0.5984
31. 1.55
33. 0.365
35. 888.8%
37. 85%
39. 168.1%
41. 14%
43. 870%
45. 38%
47. 2%
49. 4.4%
51. 50%
53. 250%
55. 160%
57. 280%
59. 450%
61. 225%
63. 140%
65. 120%
67. 240%
69. 82.76%
71. 214.3%
73. 29.17%
75. 266.7%
77. 39.1%
79. 62.96%
81.
i) Los signos negativos indican que la tasa delictiva ha disminuido con respecto a medidas anteriores.
ii) El robo de vehículos motorizados disminuyó más con una disminución de 18.75%.
iii) El robo disminuyó menos con una disminución de 2.5%.
83.
i) 4% de probabilidad de inundación
ii) 3.1% de probabilidad de inundación
iii) 25% de probabilidad de inundación
iv) 0.7% de probabilidad de inundación


