7.7: Gráficos circulares

En esta sección volvemos nuestra atención a los gráficos circulares, pero antes de hacerlo, necesitamos establecer algunos fundamentos respecto a la medición de ángulos.

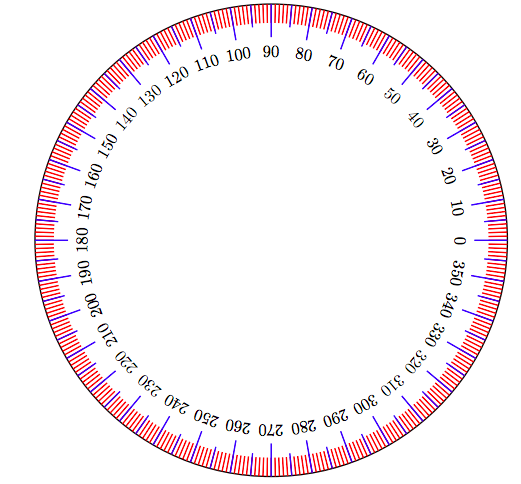
Si tomas un círculo y lo divides en 360 incrementos iguales, entonces cada incremento se llama un grado (1 ^◦). Ver Figura 7.2.

Figura 7.2: Hay 360 grados (360 ^◦) en un círculo.

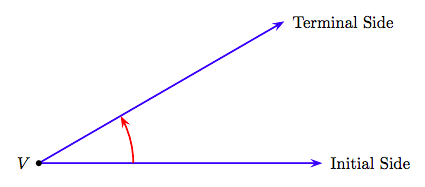
Un rayo es una línea que comienza en un punto y luego se extiende indefinidamente en una dirección. El punto de partida del rayo se llama su vértice.

Figura 7.3: Un rayo con vértice V se extiende indefinidamente en una dirección.

Si dos rayos tienen un vértice común, forman lo que se llama ángulo. En la Figura 7.4 hemos etiquetado el primer rayo como el “Lado Inicial” del ángulo, y el segundo como el “Lado Terminal” del ángulo.

Figura 7.4: Dos rayos con un vértice V común forman un ángulo.

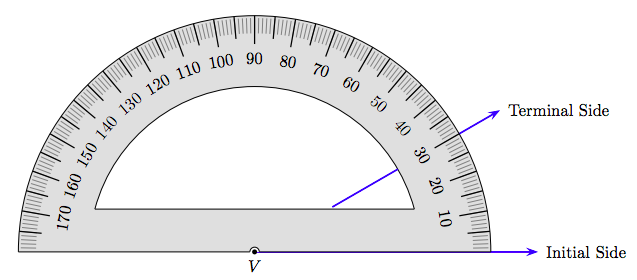
Podemos encontrar la medida de grado del ángulo mediante el uso de un dispositivo llamado un traslador. Alinee la muesca en el centro de la base del traslador con el vértice del ángulo, luego alinee la base del traslador con el lado inicial del ángulo. El lado terminal del ángulo cruzará el borde del traslador donde podemos leer la medida de grado del ángulo (ver Figura 7.5). En la Figura 7.5, nótese que el lado terminal del ángulo pasa por la marca de graduación en el número 30, indicando que la medida de grado de este ángulo es de 30 ^◦.

Figura 7.5: La medida de grado es de 30 ^◦.

Gráficos circulares

Ahora que podemos medir ángulos, podemos centrar nuestra atención en la construcción de gráficos circulares.

Gráfico circular

Un gráfico circular es un gráfico circular que se divide en sectores, representando cada sector una cantidad particular. El área de cada sector es un porcentaje del área de todo el círculo y se determina calculando la cantidad que representa como porcentaje del conjunto.

Ejemplo 1

En una reciente encuesta de Gallup, 66% de los encuestados aprobaron el desempeño laboral del Presidente, 28% desaprobaron y 6% estaban indecisos. Cree un gráfico circular que muestre estos porcentajes.

Solución

Empecemos con 6% indecisos. Queremos crear un sector que sea el 6% del área de todo el círculo. Hay 360 grados en círculo completo, por lo que 6% de este número es

\[ \begin{aligned} 6 \% \cdot 360^{ \circ} & = 0.06 \cdot 360^{ \circ} \\ ~ & = 21.6^{ \circ}. \end{aligned}\nonumber \]

Comience con un círculo, establezca la muesca de línea base del traslador en el centro del círculo, luego marque un ángulo de 21.6 ^◦, como se ve en la Figura 7.6 (a). Sombrear la región resultante como se muestra en la Figura 7.6 (b), denominada sector, que representa 6% del área total del círculo.

Figura 7.6: Sector con ángulo central 21.6 ^◦ representa el 6% de la muestra encuestadora que estaba indecisa sobre el desempeño del presidente.

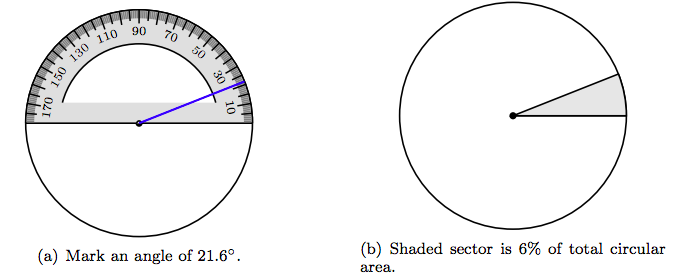
A continuación, 28% desaprobó el desempeño laboral del Presidente. Por lo tanto,

\[ \begin{aligned} 28 \% \cdot 360^{ \circ} & = 0.28 \cdot 360^{ \circ} \\ ~ & = 100.8^{ \circ}. \end{aligned}\nonumber \]

Por lo tanto, un sector con un ángulo central de 100.8 ^◦ representará 28% de desaprobación laboral.

Coloque la muesca en la línea base de su traslador en el centro del círculo, luego alinee la línea base del traslador con el lado terminal del primer ángulo, como se muestra en la Figura 7.7 (a). Marcar un ángulo central de 100.8 ^◦, como se muestra en la Figura 7.7 (a). Sombrear el segundo sector resultante con un tono más oscuro de gris, como se muestra en la Figura 7.7 (b). Este sector contiene 28% del área total del círculo y representa la porción de la muestra encuestadora que desaprobaba el desempeño laboral del presidente.

Figura 7.7: Sector con ángulo central 100.8 ^◦ representa el 28% de la muestra encuestadora que desaprobó el desempeño del presidente.

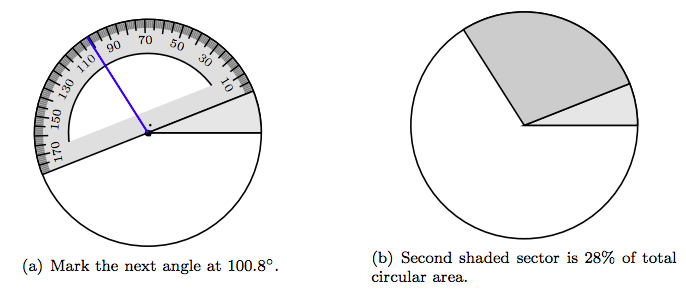
Finalmente, como hemos sombreado los sectores que representan 6% y 28% de los datos de sondeo en la Figura 7.7 (b), el sector restante en la Figura 7.7 (b), sombreado en blanco, representa el 66% de la muestra de sondeo que aprobó el desempeño laboral del presidente (y 66% del área de todo el círculo).

Una vez que haya calculado y trazado los ángulos centrales correctos para cada uno de los sectores, querrá etiquetar su gráfico circular. Un posible método de anotación se muestra en la Figura 7.8.

Figura 7.8: Anotar el gráfico circular final.

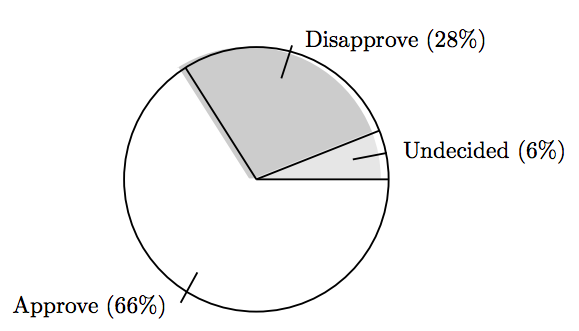
Ejercicio

En una reciente encuesta de Gallup, el 50% del público estadounidense dice que es responsabilidad del gobierno federal asegurarse de que todos los estadounidenses tengan atención médica, 47% no están de acuerdo y 3% estaban indecisos. Cree un gráfico circular que muestre estos porcentajes.

Contestar

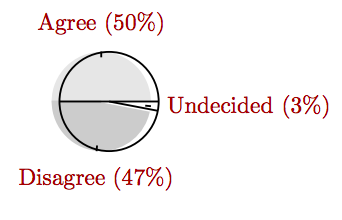
Ejemplo 2

Mil personas fueron encuestadas con la pregunta “¿Dónde duerme tu perro durante la noche?” Las respuestas se muestran en la siguiente tabla.

\[ \begin{array}{l|c} \text{Location } & \text{ Number} \\ \hline \text{Outside } & 30 \\ \text{Another Room } & 220 \\ \text{On the Bedroom Floor } & 330 \\ \text{On the Bed } & 420 \\ \hline \text{Totals } & 1000 \end{array}\nonumber \]

Crear un gráfico circular que muestre la distribución de estas respuestas.

Solución

El primer paso es expresar el número en cada ubicación como porcentaje de los totales. Por ejemplo,

\[ \begin{array}{c c c c c} \colorbox{cyan}{Outside} & \text{ is } & \colorbox{cyan}{what percent} & \text{ of } & \colorbox{cyan}{total} \\ 30 & = & p & \cdot & 1000 \end{array}\nonumber \]

Resolviendo para p,

\[ \begin{aligned} \frac{1000p}{1000} = \frac{30}{1000} ~ & \textcolor{red}{ \text{ Divide both sides by 1000.}} \\ p = 0.03 ~ & \textcolor{red}{ \text{ Divide: 30/1000 = 0.03.}} \end{aligned}\nonumber \]

Así, p = 3%. De manera similar, divide el número en cada ubicación por 1000 para encontrar los siguientes porcentajes.

\[ \begin{array}{l|c} \text{Location } & \text{ Number } & \text{ Percent} \\ \hline \text{Outside } & 30 & 3 \% \\ \text{Another Room } & 220 & 22 \% \\ \text{On the Bedroom Floor } & 330 & 33 \% \\ \text{On the Bed } & 420 & 42 \% \\ \hline \text{Totals } & 1000 & 100 \% \end{array}\nonumber \]

Tenga en cuenta que los porcentajes individuales deben sumar el 100%.

Empecemos por el hecho de que el 3% de los dueños de perros tienen sus perros duermen afuera. Para encontrar la porción del círculo completo que representa 3%, tomamos 3% de 360 ^◦.

\[ \begin{aligned} 3 \% \cdot 360^{ \circ} & = 0.03 \cdot 360^{ \circ} \\ ~ & = 10.8^{ \circ} \end{aligned}\nonumber \]

Comience con un círculo, establezca la muesca de línea base del traslador en el centro del círculo, luego marque un ángulo de 10.8 ^◦, como se ve en la Figura 7.9 (a).

Figura 7.9: Sector con ángulo central 10.8 ^◦ representa el 3% de la muestra encuestada que tiene sus perros durmiendo afuera.

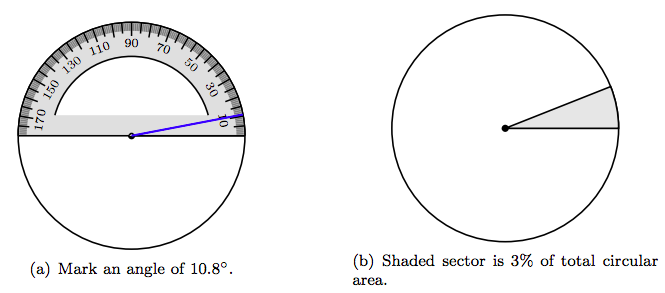
Sombrear el sector resultante como se muestra en la Figura 7.9 (b), lo que representa 3% del área total del círculo.

A continuación, 22% hace que su perro duerma en otra habitación.

\[ \begin{aligned} 22 \% \cdot 360^{ \circ} & = 0.22 \cdot 360^{ \circ} \\ ~ & = 79.2^{ \circ}. \end{aligned}\nonumber \]

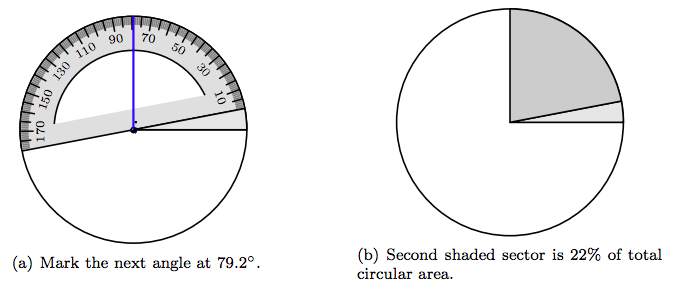
Por lo tanto, un sector con un ángulo central de 79.2 ^◦ representará el hecho de que 22% de los dueños de perros tienen su perro durmiendo en otra habitación.

Coloque la muesca en la línea base de su traslador en el centro del círculo, luego alinee la línea base del traslador con el lado terminal del primer ángulo, como se muestra en la Figura 7.10 (a). Marcar un ángulo central de 79.2◦, como se muestra en la Figura 7.7 (a). Sombrear el segundo sector resultante con un tono más oscuro de gris, como se muestra en la Figura 7.10 (b). Este sector contiene 22% del área total del círculo y representa la porción de la muestra encuestadora cuyo perro duerme en otra habitación.

A continuación, 33% permite que su perro duerma en el piso de la recámara.

\[ \begin{aligned} 33 \% \cdot 360^{ \circ} & = 0.33 \cdot 360^{ \circ} \\ ~ & = 118.8^{ \circ}. \end{aligned}\nonumber \]

Por lo tanto, un sector con un ángulo central de 118.8 ^◦ representará el hecho de que 33% de los dueños de perros permiten que su perro duerma en el piso del dormitorio.

Coloque la muesca en la línea base de su traslador en el centro del círculo, luego alinee la línea base del traslador con el lado terminal del segundo sector, como se muestra en la Figura 7.11 (a). Marcar un ángulo central de 118.8 ^◦, como se muestra en la Figura 7.11 (a). Sombrear el segundo sector resultante con un tono más oscuro de gris, como se muestra en la Figura 7.11 (b). Este sector contiene 33% del área total del círculo y representa la porción de la muestra encuestadora cuyo perro duerme en el piso del dormitorio.

Figura 7.10: Sector con ángulo central 79.2 ^◦ representa el 22% de la muestra encuestada cuyos perros duermen en otra habitación.

Figura 7.11: Sector con ángulo central 118.8 ^◦ representa el 33% de la muestra encuestada cuyos perros duermen en el piso del dormitorio.

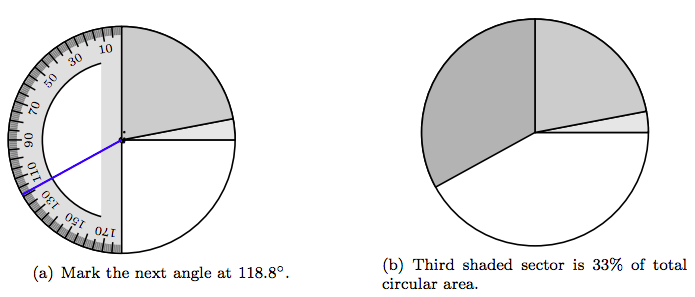
Debido a que los tres primeros sectores, sombreados en varios niveles de gris, representan 3%, 22% y 33% del área circular total, respectivamente, el sector restante (sombreado en blanco) representa automáticamente

\[100 \% − (3 \% + 22 \% + 33 \%) = 42 \%\nonumber \]

del área circular total. Esta región representa el porcentaje de dueños de perros que permiten que sus perros duerman en la cama. El resultado final, con anotaciones, se muestra en la Figura 7.1

Figura 7.12: Anotar el gráfico circular final.

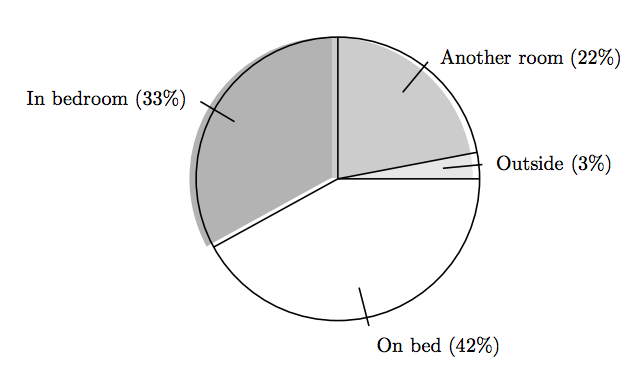
Ejercicio

A Doscientas personas se les preguntó si votaban “Sí” o “No” a la Proposición 8. Hubo 150 votos “Sí” y 50 votos “No”. Crear un gráfico circular que muestre la distribución de estas respuestas.

Contestar

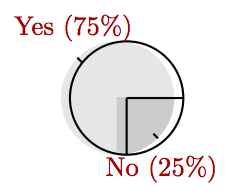
Ejercicios

1. En una elección para presidente de clase, Raven recibió 21% de los votos, Anita recibió 27%, Jamal recibió 24% de los votos, y 28% de los votos fueron recibidos por otros candidatos. Si se crea un gráfico circular para estos datos, ¿cuál será la medida de grado del ángulo central del sector que representa la participación de Raven en el voto? Redondea tu respuesta al grado más cercano.

2. En una elección para presidente de clase, Fernando recibió 26% de los votos, Luisa recibió 26%, Ali recibió 26% de los votos, y 22% de los votos fueron recibidos por otros candidatos. Si se crea un gráfico circular para estos datos, ¿cuál será la medida de grado del ángulo central del sector que representa la participación de Fernando en el voto? Redondea tu respuesta al grado más cercano.

3. En una elección para presidente de clase, Akbar recibió 23% de los votos, Ali recibió 27%, Juanita recibió 30% de los votos, y 20% de los votos fueron recibidos por otros candidatos. Si se crea un gráfico circular para estos datos, ¿cuál será la medida de grado del ángulo central del sector que representa la participación de Akbar en el voto? Redondea tu respuesta al grado más cercano.

4. En una elección para presidente de clase, Kamili recibió 21% de los votos, Bernardo recibió 22%, Fernando recibió 30% de los votos, y 27% de los votos fueron recibidos por otros candidatos. Si se crea un gráfico circular para estos datos, ¿cuál será la medida de grado del ángulo central del sector que representa la participación de Kamili en el voto? Redondea tu respuesta al grado más cercano.

5. En una elección para presidente de clase, Jamal recibió 30% de los votos, Luisa recibió 20%, Kamili recibió 28% de los votos, y 22% de los votos fueron recibidos por otros candidatos. Si se crea un gráfico circular para estos datos, ¿cuál será la medida de grado del ángulo central del sector que representa la participación de Jamal en el voto? Redondea tu respuesta al grado más cercano.

6. En una elección para presidente de clase, Juanita recibió 30% de los votos, Ali recibió 24%, Estevan recibió 24% de los votos, y 22% de los votos fueron recibidos por otros candidatos. Si se crea un gráfico circular para estos datos, ¿cuál será la medida de grado del ángulo central del sector que representa la participación de Juanita en el voto? Redondea tu respuesta al grado más cercano.

---

7. En una elección para presidente de clase, Chin recibió 5 votos, Mabel recibió 13 votos y Juanita recibió los 32 votos restantes emitidos. Si se crea un gráfico circular para estos datos de votación, ¿cuál será la medida de grado del ángulo central del sector que representa la participación de Chin en el voto? Redondea tu respuesta al grado más cercano.

8. En una elección para presidente de clase, Anita recibió 11 votos, José recibió 9 votos y Bernardo recibió los 30 votos restantes emitidos. Si se crea un gráfico circular para estos datos de votación, ¿cuál será la medida de grado del ángulo central del sector que representa la participación de Anita en el voto? Redondea tu respuesta al grado más cercano.

9. En una elección para presidente de clase, Kamili recibió 14 votos, Jamal recibió 9 votos y José recibió los 27 votos restantes emitidos. Si se crea un gráfico circular para estos datos de votación, ¿cuál será la medida de grado del ángulo central del sector que representa la participación de Kamili en el voto? Redondea tu respuesta al grado más cercano.

10. En una elección para presidente de clase, Jun recibió 13 votos, Abdul recibió 15 votos y Raven recibió los 22 votos restantes emitidos. Si se crea un gráfico circular para estos datos de votación, ¿cuál será la medida de grado del ángulo central del sector que representa la participación de Jun en la votación? Redondea tu respuesta al grado más cercano.

11. En una elección para presidente de clase, Hue recibió 13 votos, Ali recibió 6 votos y Henry recibió los 31 votos restantes emitidos. Si se crea un gráfico circular para estos datos de votación, ¿cuál será la medida de grado del ángulo central del sector que representa la participación de Hue en el voto? Redondea tu respuesta al grado más cercano.

12. En una elección para presidente de clase, Mercy recibió 9 votos, Bernardo recibió 7 votos y Hans recibió los 34 votos restantes emitidos. Si se crea un gráfico circular para estos datos de votación, ¿cuál será la medida de grado del ángulo central del sector que representa la participación de Mercy en el voto? Redondea tu respuesta al grado más cercano.

---

13. En una elección para presidente de clase, la distribución de votos entre tres candidatos se muestra en el siguiente gráfico circular.

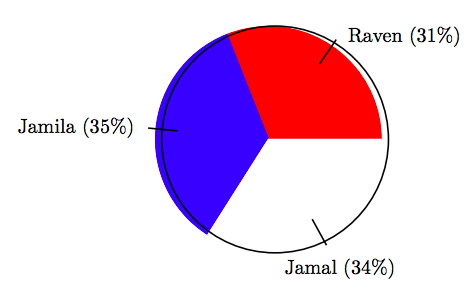
Si hubo un total de 95 votos emitidos en la elección, encuentre el número de votos que recibió Raven, correcto al voto más cercano.

14. En una elección para presidente de clase, la distribución de votos entre tres candidatos se muestra en el siguiente gráfico circular.

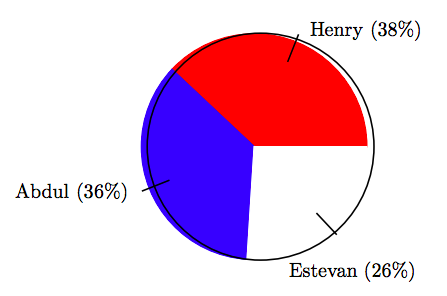
Si hubo un total de 79 votos emitidos en la elección, encuentre el número de votos que recibió Henry, correcto al voto más cercano.

15. En una elección para presidente de clase, la distribución de votos entre tres candidatos se muestra en el siguiente gráfico circular.

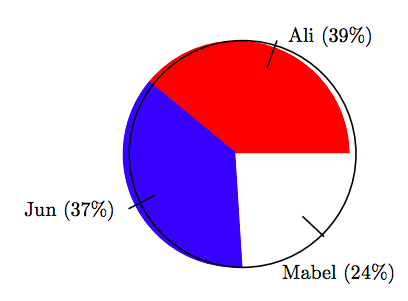
Si hubo un total de 58 votos emitidos en la elección, encuentre el número de votos que recibió Ali, correcto al voto más cercano.

16. En una elección para presidente de clase, la distribución de votos entre tres candidatos se muestra en el siguiente gráfico circular.

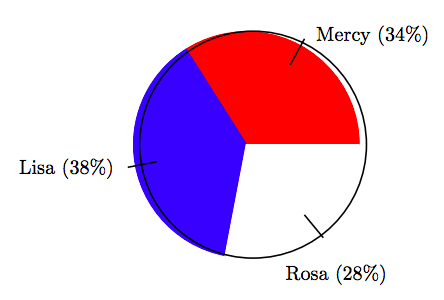
Si hubo un total de 65 votos emitidos en la elección, encuentre el número de votos que recibió Mercy, correcto al voto más cercano.

17. En una elección para presidente de clase, la distribución de votos entre tres candidatos se muestra en el siguiente gráfico circular.

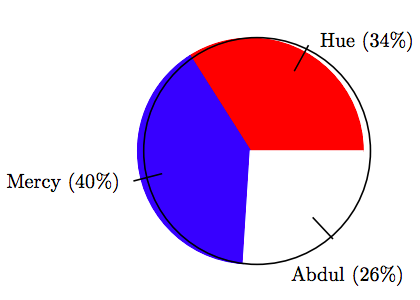
Si hubo un total de 95 votos emitidos en la elección, encuentre el número de votos que recibió Hue, correcto al voto más cercano.

18. En una elección para presidente de clase, la distribución de votos entre tres candidatos se muestra en el siguiente gráfico circular.

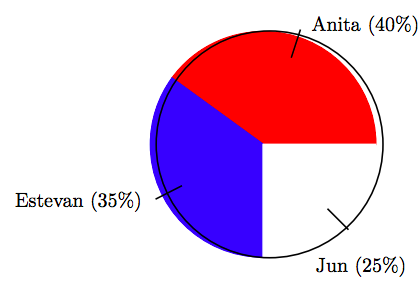
Si hubo un total de 75 votos emitidos en la elección, encuentre el número de votos que recibió Anita, correctos al voto más cercano.

---

19. En una elección para presidente de clase, la distribución de votos entre tres candidatos se muestra en la siguiente tabla.

\[ \begin{array}{c|c|c|c} \text{Candidate } & \text{ Votes } \\ \hline \text{Ali } & 45 \\ \text{Jamal } & 34 \\ \text{Jun } & 52 \\ \hline \end{array}\nonumber \]

Use un desplazador para ayudar a crear un gráfico circular que muestre la distribución de votos.

20. En una elección para presidente de clase, la distribución de votos entre tres candidatos se muestra en la siguiente tabla.

\[ \begin{array}{c|c|c|c} \text{Candidate } & \text{ Votes } \\ \hline \text{Aisha } & 39 \\ \text{Akbar } & 31 \\ \text{Fernando } & 36 \\ \hline \end{array}\nonumber \]

Use un desplazador para ayudar a crear un gráfico circular que muestre la distribución de votos.

21. En una elección para presidente de clase, la distribución de votos entre tres candidatos se muestra en la siguiente tabla.

\[ \begin{array}{c|c|c|c} \text{Candidate } & \text{ Votes } \\ \hline \text{Bernardo } & 44 \\ \text{Rosa } & 40 \\ \text{Abdul } & 58 \\ \hline \end{array}\nonumber \]

Use un desplazador para ayudar a crear un gráfico circular que muestre la distribución de votos.

22. En una elección para presidente de clase, la distribución de votos entre tres candidatos se muestra en la siguiente tabla.

\[ \begin{array}{c|c|c|c} \text{Candidate } & \text{ Votes } \\ \hline \text{Estevan } & 46 \\ \text{Ali } & 58 \\ \text{Henry } & 49 \\ \hline \end{array}\nonumber \]

Use un desplazador para ayudar a crear un gráfico circular que muestre la distribución de votos.

23. En una elección para presidente de clase, la distribución de votos entre tres candidatos se muestra en la siguiente tabla.

\[ \begin{array}{c|c|c|c} \text{Candidate } & \text{ Votes } \\ \hline \text{Mercy } & 56 \\ \text{Hans } & 53 \\ \text{Lisa } & 41 \\ \hline \end{array}\nonumber \]

Use un traslador para ayudar a crear un gráfico circular que muestre la distribución de votos.

24. En una elección para presidente de clase, la distribución de votos entre tres candidatos se muestra en la siguiente tabla.

\[ \begin{array}{c|c|c|c} \text{Candidate } & \text{ Votes } \\ \hline \text{Estevan } & 60 \\ \text{Hue } & 33 \\ \text{Aisha } & 31 \\ \hline \end{array}\nonumber \]

Use un traslador para ayudar a crear un gráfico circular que muestre la distribución de votos.

25. En una elección para presidente de clase, la distribución de votos entre tres candidatos se muestra en la siguiente tabla.

\[ \begin{array}{c|c|c|c} \text{Candidate } & \text{ Votes } \\ \hline \text{Raven } & 43 \\ \text{Mabel } & 40 \\ \text{Bernardo } & 52 \\ \hline \end{array}\nonumber \]

Use un traslador para ayudar a crear un gráfico circular que muestre la distribución de votos.

26. En una elección para presidente de clase, la distribución de votos entre tres candidatos se muestra en la siguiente tabla.

\[ \begin{array}{c|c|c|c} \text{Candidate } & \text{ Votes } \\ \hline \text{Hue } & 48 \\ \text{Lisa } & 48 \\ \text{Akbar } & 47 \end{array}\nonumber \]

Use un traslador para ayudar a crear un gráfico circular que muestre la distribución de votos.

27. En una elección para presidente de clase, la distribución de votos entre tres candidatos se muestra en la siguiente tabla.

\[ \begin{array}{c|c|c|c} \text{Candidate } & \text{ Votes } \\ \hline \text{Jun } & 57 \\ \text{Lisa } & 30 \\ \text{Aisha } & 58 \\ \hline \end{array}\nonumber \]

Use un traslador para ayudar a crear un gráfico circular que muestre la distribución de votos.

28. En una elección para presidente de clase, la distribución de votos entre tres candidatos se muestra en la siguiente tabla.

\[ \begin{array}{c|c|c|c} \text{Candidate } & \text{ Votes } \\ \hline \text{Bernardo } & 54 \\ \text{Mabel } & 38 \\ \text{Henry } & 49 \\ \hline \end{array}\nonumber \]

Use un traslador para ayudar a crear un gráfico circular que muestre la distribución de votos.

29. En una elección para presidente de clase, la distribución de votos entre tres candidatos se muestra en la siguiente tabla.

\[ \begin{array}{c|c|c|c} \text{Candidate } & \text{ Votes } \\ \hline \text{Henry } & 35 \\ \text{Bernardo } & 32 \\ \text{Estevan } & 47 \\ \hline \end{array}\nonumber \]

Use un traslador para ayudar a crear un gráfico circular que muestre la distribución de votos.

30. En una elección para presidente de clase, la distribución de votos entre tres candidatos se muestra en la siguiente tabla.

\[ \begin{array}{c|c|c|c} \text{Candidate } & \text{ Votes } \\ \hline \text{Bernardo } & 38 \\ \text{Fernando } & 49 \\ \text{Aisha } & 44 \\ \hline \end{array}\nonumber \]

Use un traslador para ayudar a crear un gráfico circular que muestre la distribución de votos.

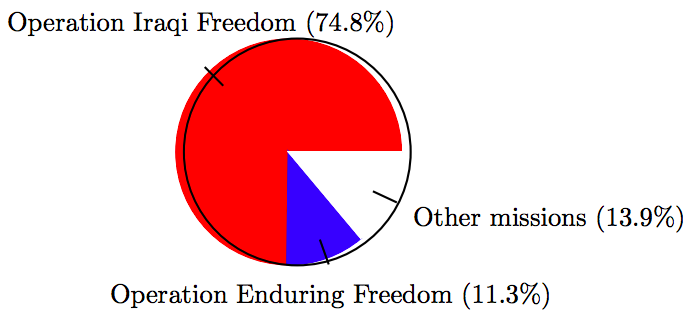
31. Despliegue de guardia. En la tabla se muestra el número de servicios de tropas de guardia desde el 11 de septiembre de 2001 (a diciembre de 2008; algunas tropas se han activado varias veces). Associated Press-Times-Standard 02/18/10 Tropas de la Guardia esperan el pago prometido.

\[ \begin{array}{c|c|c|c} \text{Mission } & \text{ Troops } \\ \hline \text{Operation Iraqi Freedom } & 193,598 \\ \text{Operation Enduring Freedom } & 29,212 \\ \text{Other missions } & 35,849 \\ \hline \end{array}\nonumber \]

Usa un traslador para ayudar a crear un gráfico circular que muestre la distribución de las tropas de la Guardia Nacional.

---

RESPUESTAS

1. 76 ^◦

3. 83 ^◦

5. 108 ^◦

7. 36 ^◦

9. 101 ^◦

11. 94 ^◦

13. 29 votos

15. 23 votos

17. 32 votos

19.

\[ \begin{array}{c|c|c|c} \text{Candidate } & \text{ Votes } & \text{ Percent } & \text{ Degrees } \\ \hline \text{Ali } & 45 & 34.4 \% & 123.84^{ \circ} \\ \text{Jamal } & 34 & 26.0 \% & 93.6^{ \circ} \\ \text{Jun } & 52 & 39.7 \% & 142.92 \\ \hline \end{array}\nonumber \]

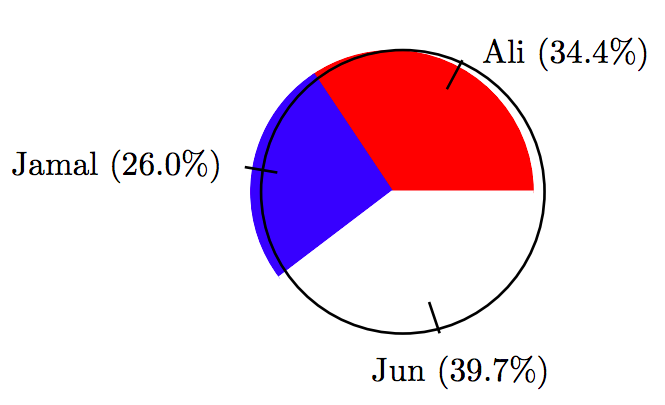
21.

\[ \begin{array}{c|c|c|c} \text{Candidate } & \text{ Votes } & \text{ Percent } & \text{ Degrees } \\ \hline \text{Bernardo } & 44 & 31.0 \% & 111.6^{ \circ} \\ \text{Rosa } & 40 & 28.2 \% & 101.52^{ \circ} \\ \text{Abdul } & 58 & 40.8 \% & 146.88^{ \circ} \\ \hline \end{array}\nonumber \]

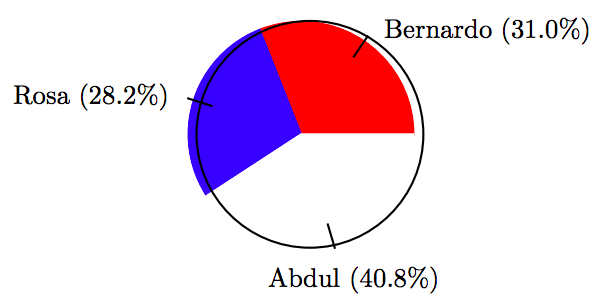
23.

\[ \begin{array}{c|c|c|c} \text{Candidate } & \text{ Votes } & \text{ Percent } & \text{ Degrees } \\ \hline \text{Mercy } & 56 & 37.3 \% & 134.28^{ \circ} \\ \text{Hans } & 53 & 35.3 \% & 127.08^{ \circ} \\ \text{Lisa } & 41 & 27.3 \% & 98.28^{ \circ} \\ \hline \end{array}\nonumber \]

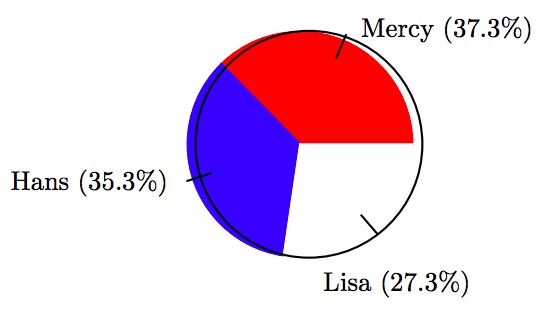
25.

\[ \begin{array}{c|c|c|c} \text{Candidate } & \text{ Votes } & \text{ Percent } & \text{ Degrees } \\ \hline \text{Raven } & 43 & 31.9 \% & 114.84^{ \circ} \\ \text{Mabel } & 40 & 29.6 \% & 106.56^{ \circ} \\ \text{Bernardo } & 52 & 38.5 \% & 138.6^{ \circ} \\ \hline \end{array}\nonumber \]

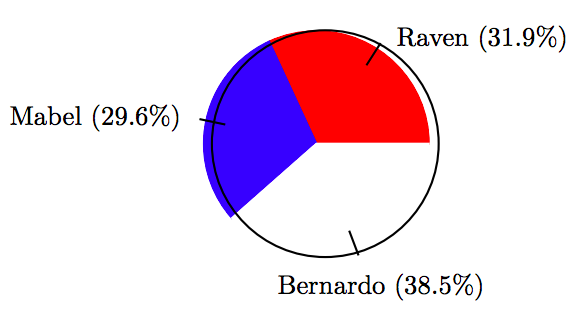
27.

\[ \begin{array}{c|c|c|c} \text{Candidate } & \text{ Votes } & \text{ Percent } & \text{ Degrees } \\ \hline \text{Jun } & 57 & 39.3 \% & 141.48^{ \circ} \\ \text{Lisa } & 30 & 20.7 \% & 74.52^{ \circ} \\ \text{Aisha } & 58 & 40.0 \% & 144^{ \circ} \\ \hline \end{array}\nonumber \]

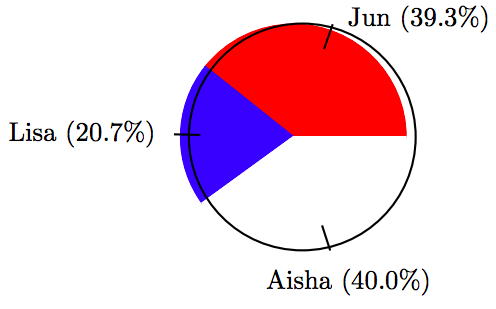
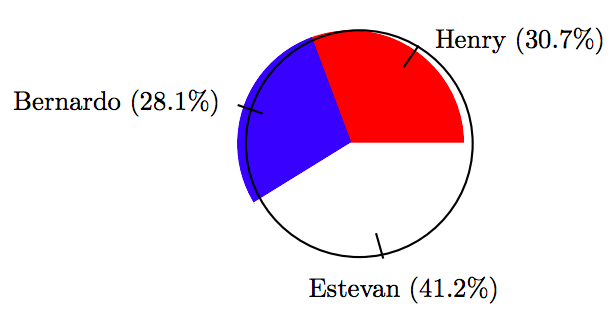
29.

\[ \begin{array}{c|c|c|c} \text{Candidate } & \text{ Votes } & \text{ Percent } & \text{ Degrees } \\ \hline \text{Henry } & 35 & 30.7 \% & 110.52^{ \circ} \\ \text{Bernardo } & 32 & 28.1 \% & 101.16^{ \circ} \\ \text{Estevan } & 47 & 41.2 \% & 148.32^{ \circ} \\ \hline \end{array}\nonumber \]

31.

\[ \begin{array}{c|c|c|c} \text{Mission } & \text{ Troops } & \text{ Percent } & \text{ Degrees } \\ \hline \text{Operation Iraqi Freedom } & 193,598 & 74.8 \% & 269.28^{ \circ} \\ \text{Operation Enduring Freedom } & 29,212 & 11.3 \% & 40.68^{ \circ} \\ \text{Other missions } & 35,849 & 13.9 \% & 50.04^{ \circ} \\ \hline \end{array}\nonumber \]