6.1: Entender por ciento
- Page ID
- 114301
- Usa la definición de porcentaje
- Convertir porcentajes en fracciones y decimales
- Convertir decimales y fracciones en porcentajes
Antes de comenzar, toma este cuestionario de preparación.
- Traducir “la relación de 33 a 5” en una expresión algebraica. Si te perdiste este problema, revisa la Tabla 2.4.3.
- Escribe 3 5 como decimal. Si te perdiste este problema, revisa el Ejemplo 5.5.1.
- Escribe 0.62 como fracción. Si te perdiste este problema, revisa el Ejemplo 5.1.4.
Usar la Definición de Porcentaje
¿Cuántos centavos hay en un dólar? Hay 100 centavos en un dólar. ¿Cuántos años hay en un siglo? Hay 100 años en un siglo. ¿Esto te da una pista sobre lo que significa la palabra “por ciento”? Realmente son dos palabras, “por ciento”, y significa por cien. Un por ciento es una relación cuyo denominador es 100. Utilizamos el símbolo de porcentaje%, para mostrar el porcentaje.
Un por ciento es una relación cuyo denominador es 100.
Según datos de la Asociación Americana de Colegios Comunitarios (2015), alrededor del 57% de los estudiantes de colegios comunitarios son mujeres. Esto significa que 57 de cada 100 estudiantes de colegios comunitarios son mujeres, como\(\PageIndex{1}\) muestra la Figura. De los 100 cuadrados de la cuadrícula, 57 están sombreados, lo que escribimos como la proporción\(\dfrac{57}{100}\).
Figura\(\PageIndex{1}\) - De cada 100 estudiantes de colegios comunitarios, 57 son mujeres.
De igual manera, 25% significa una relación de\(\dfrac{25}{100}\), 3% significa una relación de\(\dfrac{3}{100}\) y 100% significa una relación de\(\dfrac{100}{100}\). En palabras, “cien por ciento” significa que el total 100% es\(\dfrac{100}{100}\), y como\(\dfrac{100}{100}\) = 1, vemos que 100% significa 1 entero.
De acuerdo con el Instituto de Políticas Públicas de California (2010), 44% de los padres de los niños de escuelas públicas les gustaría que su hijo menor obtuviera un título de posgrado. Escribe este porcentaje como una proporción.
Solución
| La cantidad que queremos convertir es de 44%. | 44% |
| Escribe el porcentaje como proporción. Recuerda que por ciento significa por cada 100. | $$\ dfrac {44} {100} $$ |
Escribe el porcentaje como proporción. Según una encuesta, el 89% de los estudiantes universitarios tienen un teléfono inteligente.
- Contestar
-
\(\frac{89}{100}\)
Escribe el porcentaje como proporción. Un estudio encontró que 72% de los adolescentes estadounidenses envían mensajes de texto regularmente.
- Contestar
-
\(\frac{72}{100}\)
En 2007, según un informe del Departamento de Educación de Estados Unidos, 21 de cada 100 estudiantes universitarios primerizos de primer año en instituciones públicas de 4 años tomaron al menos un curso correctivo. Escribe esto como una proporción y luego como un porcentaje.
Solución
| La cantidad que queremos convertir es 21 de 100. | 21 de 100 |
| Escribir como una relación. | $$\ dfrac {21} {100} $$ |
| Convierta el 21 por 100 a por ciento. | 21% |
Escribir como proporción y luego como porcentaje: La Asociación Americana de Colegios Comunitarios informó que 62 de cada 100 estudiantes de colegios comunitarios de tiempo completo equilibran sus estudios con un empleo a tiempo completo o a tiempo parcial.
- Contestar
-
\(\frac{62}{100}\), 62%
Escribir como proporción y luego como porcentaje: En respuesta a una encuesta estudiantil, 41 de cada 100 estudiantes de Santa Ana College expresaron el objetivo de obtener un título de Asociado o trasladarse a una universidad de cuatro años.
- Contestar
-
\(\frac{41}{100}\), 41%
Convertir porcentajes a fracciones y decimales
Dado que los porcentajes son proporciones, se pueden expresar fácilmente como fracciones. Recuerda que por ciento significa por 100, por lo que el denominador de la fracción es 100.
Paso 1. Escribe el porcentaje como una relación con el denominador 100.
Paso 2. Simplifique la fracción si es posible.
Convertir cada porcentaje a una fracción: (a) 36% (b) 125%
Solución
a) 36%
| Escribir como una relación con denominador 100. | $$\ dfrac {36} {100} $$ |
| Simplificar. | $$\ dfrac {9} {25} $$ |
b) 125%
| Escribir como una relación con denominador 100. | $$\ dfrac {125} {100} $$ |
| Simplificar. | $$\ dfrac {5} {4} $$ |
Convertir cada porcentaje en una fracción: (a) 48% (b) 110%
- Contestar a
-
\(\frac{12}{25}\)
- Respuesta b
-
\(\frac{11}{10}\)
Convertir cada porcentaje en una fracción: (a) 64% (b) 150%
- Contestar a
-
\(\frac{16}{25}\)
- Respuesta b
-
\(\frac{3}{2}\)
El ejemplo anterior muestra que un porcentaje puede ser mayor que 1. Vimos que 125% significa\(\dfrac{125}{100}\), o\(\dfrac{5}{4}\). Se trata de fracciones impropias, y sus valores son mayores que uno.
Convertir cada porcentaje en una fracción: (a) 24.5% (b) 33\(\dfrac{1}{3}\)%
Solución
(a) 24.5%
| Escribir como una relación con denominador 100. | $$\ dfrac {24.5} {100} $$ |
| Borra el decimal multiplicando el numerador y el denominador por 10. | $$\ dfrac {24.5 (10)} {100 (10)} $$ |
| Multiplicar. | $$\ dfrac {245} {1000} $$ |
| Reescritura mostrando factores comunes. | $$\ dfrac {5\ cdot 49} {5\ cdot 200} $$ |
| Simplificar. | $$\ dfrac {49} {200} $$ |
b) 33\(\dfrac{1}{3}\)%
| Escribir como una relación con denominador 100. | $$\ dfrac {33\ dfrac {1} {3}} {100} $$ |
| Escribe el numerador como una fracción impropia. | $$\ dfrac {\ dfrac {100} {3}} {100} $$ |
| Reescribir como división de fracciones, reemplazando 100 por\(\dfrac{100}{1}\). | $$\ dfrac {100} {3}\ div\ dfrac {100} {1} $$ |
| Multiplicar por el recíproco. | $$\ dfrac {100} {3}\ cdot\ dfrac {1} {100} $$ |
| Simplificar. | $$\ dfrac {1} {3} $$ |
Convertir cada porcentaje a una fracción: (a) 64.4% (b) 66\(\dfrac{2}{3}\)%
- Contestar a
-
\(\frac{161}{250}\)
- Respuesta b
-
\(\frac{2}{3}\)
Convertir cada porcentaje en una fracción: (a) 42.5% (b) 8\(\dfrac{3}{4}\)%
- Contestar a
-
\(\frac{113}{250}\)
- Respuesta b
-
\(\frac{7}{80}\)
En Decimales aprendimos a convertir fracciones a decimales. Para convertir un porcentaje a un decimal, primero lo convertimos a una fracción y luego cambiamos la fracción a un decimal.
Paso 1. Escribe el porcentaje como una relación con el denominador 100.
Paso 2. Convierte la fracción a decimal dividiendo el numerador por el denominador.
Convertir cada porcentaje a un decimal: (a) 6% (b) 78%
Solución
Debido a que queremos cambiar a un decimal, dejaremos las fracciones con denominador 100 en lugar de eliminar factores comunes.
(a) 6%
| Escribir como una relación con denominador 100. | $$\ dfrac {6} {100} $$ |
| Cambiar la fracción a un decimal dividiendo el numerador por el denominador. | 0.06 |
b) 78%
| Escribir como una relación con denominador 100. | $$\ dfrac {78} {100} $$ |
| Cambiar la fracción a un decimal dividiendo el numerador por el denominador. | 0.78 |
Convertir cada porcentaje a un decimal: (a) 9% (b) 87%
- Contestar a
-
\(0.09\)
- Respuesta b
-
\(0.87\)
Convertir cada porcentaje a un decimal: (a) 3% (b) 91%
- Contestar a
-
\(0.03\)
- Respuesta b
-
\(0.91\)
Convertir cada porcentaje a un decimal: (a) 135% (b) 12.5%
Solución
| Escribir como una relación con denominador 100. | $$\ dfrac {135} {100} $$ |
| Cambiar la fracción a un decimal dividiendo el numerador por el denominador. | 1.35 |
b) 12.5%
| Escribir como una relación con denominador 100. | $$\ dfrac {12.5} {100} $$ |
| Cambiar la fracción a un decimal dividiendo el numerador por el denominador. | 0.125 |
Convertir cada porcentaje a un decimal: (a) 115% (b) 23.5%
- Contestar a
-
\(1.15\)
- Respuesta b
-
\(0.235\)
Convertir cada porcentaje a un decimal: (a) 123% (b) 16.8%
- Contestar a
-
\(1.23\)
- Respuesta b
-
\(0.168\)
Resumamos los resultados de los ejemplos anteriores en Table\(\PageIndex{1}\), y busquemos un patrón que podamos usar para convertir rápidamente un número porcentual a un número decimal.
| Por ciento | Decimal |
|---|---|
| 6% | 0.06 |
| 78% | 0.78 |
| 135% | 1.35 |
| 12.5% | 0.125 |
¿Ves el patrón? Para convertir un número porcentual a un número decimal, movemos el punto decimal dos lugares a la izquierda y eliminamos el signo%. (A veces el punto decimal no aparece en el número de porcentaje, pero al igual que podemos pensar en el entero 6 como 6.0, podemos pensar en 6% como 6.0%.) Observe que es posible que necesitemos sumar ceros delante del número al mover el decimal hacia la izquierda.
La figura\(\PageIndex{2}\) usa los porcentajes en Tabla\(\PageIndex{1}\) y muestra visualmente cómo convertirlos a decimales moviendo el punto decimal dos lugares hacia la izquierda.
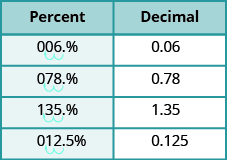
Figura\(\PageIndex{2}\)
Entre un grupo de líderes empresariales, el 77% cree que la mala educación en matemáticas y ciencias en Estados Unidos conducirá a mayores tasas de desempleo. Convertir el porcentaje a: (a) una fracción (b) a decimal
Solución
a)
| Escribir como una relación con denominador 100. | $$\ dfrac {77} {100} $$ |
b)
| Cambiar la fracción a un decimal dividiendo el numerador por el denominador. | 0.77 |
La participación de Twitter en el tráfico web saltó 24% cuando una celebridad tuiteó en vivo al aire. Convertir el porcentaje a: (a) una fracción y (b) un decimal.
- Responder a
-
\(\frac{6}{25}\)
- Respuesta b
-
\(0.24\)
El censo de Estados Unidos estimó que en 2013, 44% de la población de Boston de 25 años o más tiene títulos de licenciatura o superiores. Convertir el porcentaje a: (a) una fracción y (b) un decimal.
- Responder a
-
\(\frac{22}{50}\)
- Respuesta b
-
\(0.44\)
Hay cuatro palos de cartas en una baraja de cartas: corazones, diamantes, palos y espadas. La probabilidad de elegir aleatoriamente un corazón de una baraja de cartas barajada es del 25%. Convertir el porcentaje a: (a) una fracción (b) a decimal.
Figura\(\PageIndex{3}\) - (crédito: Riles32807, Wikimedia Commons)
Solución
a)
| Escribir como una relación con denominador 100. | $$\ dfrac {25} {100} $$ |
| Simplificar. | $$\ dfrac {1} {4} $$ |
b)
| Cambiar la fracción a un decimal dividiendo el numerador por el denominador. | 0.25 |
La probabilidad de que llueva el lunes es de 30%. Convertir el porcentaje a: (a) una fracción, y (b) un decimal.
- Responder a
-
\(\frac{3}{10}\)
- Respuesta b
-
\(0.3\)
La probabilidad de meter cabezas tres veces al lanzar una moneda tres veces es de 12.5%. Convertir el porcentaje a: (a) una fracción, y (b) un decimal.
- Responder a
-
\(\frac{12.5}{100}\)
- Respuesta b
-
\(0.125\)
Convertir decimales y fracciones a porcentajes
Para convertir un decimal a un por ciento, recuerde que por ciento significa por cien. Si cambiamos el decimal a una fracción cuyo denominador es 100, es fácil cambiar esa fracción a un porcentaje.
Paso 1. Escribe el decimal como una fracción.
Paso 2. Si el denominador de la fracción no es 100, reescribirlo como fracción equivalente con denominador 100.
Paso 3. Escribe esta relación como un porcentaje.
Convertir cada decimal a un porcentaje: (a) 0.05 (b) 0.83
Solución
(a) 0.05
| Escribir como una fracción. El denominador es 100. | $$\ dfrac {5} {100} $$ |
| Escribe esta relación como un porcentaje. | 5% |
b)
| El denominador es 100. | $$\ dfrac {83} {100} $$ |
| Escribe esta relación como un porcentaje. | 83% |
Convertir cada decimal a un porcentaje: (a) 0.01 (b) 0.17.
- Responder a
-
1%
- Respuesta b
-
17%
Convertir cada decimal a un porcentaje: (a) 0.04 (b) 0.41.
- Responder a
-
4%
- Respuesta b
-
41%
Para convertir un número mixto a un porcentaje, primero lo escribimos como una fracción impropia.
Convertir cada decimal a un porcentaje: (a) 1.05 (b) 0.075
Solución
a) 1.05
| Escribir como una fracción. | $$1\ dfrac {5} {100} $$ |
| Escribir como una fracción impropia. El denominador es 100. | $$\ dfrac {105} {100} $$ |
| Escribe esta relación como un porcentaje. | 105% |
Observe que desde 1.05 > 1, el resultado es superior al 100%.
b) 0.075
| Escribir como una fracción. | $$\ dfrac {75} {1,000} $$ |
| Divide el numerador y el denominador entre 10, de modo que el denominador sea 100. | $$\ dfrac {7.5} {100} $$ |
| Escribe esta relación como un porcentaje. | 7.5% |
Convertir cada decimal a un porcentaje: (a) 1.75 (b) 0.0825
- Responder a
-
175%
- Respuesta b
-
8.25%
Convertir cada decimal a un porcentaje: (a) 2.25 (b) 0.0925
- Responder a
-
225%
- Respuesta b
-
9.25%
Resumimos los resultados de los ejemplos anteriores en la Tabla 6.20 para que podamos buscar un patrón.
| Decimal | Por ciento |
|---|---|
| 0.05 | 5% |
| 0.83 | 83% |
| 1.05 | 105% |
| 0.075 | 7.5% |
¿Ves el patrón? Para convertir un decimal a un porcentaje, movemos el punto decimal dos lugares a la derecha y luego agregamos el signo de porcentaje.
Figura\(\PageIndex{4}\) usa los números decimales en Tabla\(\PageIndex{2}\) y muestra visualmente para convertirlos a porcentajes moviendo el punto decimal dos lugares a la derecha y luego escribiendo el signo%.
Figura\(\PageIndex{4}\)
En Decimales aprendimos a convertir fracciones a decimales. Ahora también sabemos cómo cambiar decimales a porcentajes. Entonces, para convertir una fracción a un porcentaje, primero la cambiamos a un decimal y luego convertimos ese decimal a un porcentaje.
Paso 1. Convierte la fracción a decimal.
Paso 2. Convertir el decimal a un porcentaje.
Convertir cada fracción o número mixto a un porcentaje: (a)\(\dfrac{3}{4}\) (b)\(\dfrac{11}{8}\) (c)\(2 \dfrac{1}{5}\)
Solución
Para convertir una fracción en decimal, divida el numerador por el denominador.
a)
| Cambiar a un decimal. | $$\ dfrac {3} {4} $$ |
| Escribe como un porcentaje moviendo los decimales dos lugares. |  |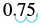
| 75% |
b)
| Cambiar a un decimal. | $$\ dfrac {11} {8} $$ |
| Escribe como un porcentaje moviendo los decimales dos lugares. |  |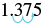
| 137.5% |
c)
| Escribir como una fracción impropia. | $$2\ dfrac {1} {5} $$ |
| Cambiar a un decimal. | $$\ dfrac {11} {5} $$ |
| Escribir como porcentaje. |  |
| 220% |
Observe que necesitábamos agregar ceros al final del número al mover los dos decimales hacia la derecha.
Convertir cada fracción o número mixto a un porcentaje: (a)\(\dfrac{5}{8}\) (b)\(\dfrac{11}{4}\) (c)\(3 \dfrac{2}{5}\)
- Responder a
-
62.5%
- Respuesta b
-
275%
- Respuesta c
-
340%
Convertir cada fracción o número mixto a un porcentaje: (a)\(\dfrac{7}{8}\) (b)\(\dfrac{9}{4}\) (c)\(1 \dfrac{3}{5}\)
- Responder a
-
87.5%
- Respuesta b
-
225%
- Respuesta c
- 160%
A veces al cambiar una fracción a un decimal, la división continúa por muchos decimales y redondearemos el cociente. El número de decimales a los que redondeamos dependerá de la situación. Si el decimal involucra dinero, redondeamos al lugar de centésimas. Para la mayoría de los demás casos en este libro redondearemos el número a la milésima más cercana, por lo que el porcentaje se redondeará a la décima más cercana.
Convertir\(\dfrac{5}{7}\) a un porcentaje.
Solución
Para cambiar una fracción a decimal, dividimos el numerador por el denominador.
| Cambiar a un decimal—redondeo a la milésima más cercana. | 0.714 |
| Escribir como porcentaje. | 71.4% |
Convertir la fracción a un porcentaje:\(\dfrac{3}{7}\)
- Contestar
- 42.9%
Convertir la fracción a un porcentaje:\(\dfrac{4}{7}\)
- Contestar
-
57.1%
Cuando miramos por primera vez fracciones y decimales, vimos que las fracciones se convertían a un decimal repetido. Cuando convertimos la fracción\(\dfrac{4}{3}\) a decimal, escribimos la respuesta como 1. \(\overline{3}\). Usaremos esta misma notación, así como notación de fracciones, cuando convertiremos fracciones a porcentajes en el siguiente ejemplo.
Un artículo en una revista médica afirmó que aproximadamente\(\dfrac{1}{3}\) de los adultos estadounidenses son obesos. Convertir la fracción\(\dfrac{1}{3}\) a un porcentaje.
Solución
| Cambiar a un decimal. |  |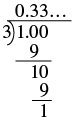
| Escribir como decimal repetitivo. | 0.333... |
| Escribir como porcentaje. | \(33 \dfrac{1}{3}\)% |
También podríamos escribir el porcentaje como 33. \(\overline{3}\)%.
Según la Oficina del Censo de Estados Unidos, aproximadamente\(\dfrac{1}{9}\) de las unidades de vivienda de Estados Unidos tienen solo 1 recámara. Convertir la fracción a un porcentaje.
- Contestar
-
\(11. \overline{1} \%\), o\(11 \frac{1}{9} \% \)
Según la Oficina del Censo de Estados Unidos, aproximadamente\(\dfrac{1}{6}\) de los residentes de Colorado hablan un idioma que no sea el inglés en casa. Convertir la fracción a un porcentaje.
- Contestar
-
\(16. \overline{6} \%\), o\(16 \frac{2}{3} \% \)
La práctica hace la perfección
Usar la definición de porcentajes
En los siguientes ejercicios, escriba cada porcentaje como una proporción.
- En 2014, la tasa de desempleo para quienes solo tenían un título de preparatoria era de 6.0%.
- En 2015, entre los desempleados, 29% estaban desempleados de larga duración.
- La tasa de desempleo para los licenciados fue de 3.2% en 2014.
- La tasa de desempleo en Michigan en 2014 fue de 7.3%.
En los siguientes ejercicios, escriba como (a) una proporción y (b) un por ciento.
- 57 de cada 100 candidatos a enfermería recibieron su título en un colegio comunitario.
- 80 de cada 100 bomberos y agentes del orden fueron educados en un colegio comunitario.
- 42 de cada 100 estudiantes de primer año asisten a un colegio comunitario.
- 71 de cada 100 profesores de colegios comunitarios de tiempo completo tienen una maestría.
Convertir porcentajes a fracciones y decimales
En los siguientes ejercicios, convierta cada porcentaje a una fracción y simplifique todas las fracciones.
- 4%
- 8%
- 17%
- 19%
- 52%
- 78%
- 125%
- 135%
- 37.5%
- 42.5%
- 18.4%
- 46.4%
- \(9 \dfrac{1}{2}\)%
- \(8 \dfrac{1}{2}\)%
- \(5 \dfrac{1}{3}\)%
- \(6 \dfrac{2}{3}\)%
En los siguientes ejercicios, convertir cada porcentaje a un decimal.
- 5%
- 9%
- 1%
- 2%
- 63%
- 71%
- 40%
- 50%
- 115%
- 125%
- 150%
- 250%
- 21.4%
- 39.3%
- 7.8%
- 6.4%
En los siguientes ejercicios, convertir cada porcentaje a (a) una fracción simplificada y (b) a un decimal.
- En 2010, 1.5% de las ventas de viviendas contaban con financiamiento de propietarios. (Fuente: Bloomberg Businessweek, 5/ 23—29/2011)
- En 2000, 4.2% de la población de Estados Unidos era de ascendencia asiática. (Fuente: www.census.gov)
- Según datos del gobierno, en 2013 el número de celulares en la India era del 70.23% de la población.
- Según la Oficina del Censo de Estados Unidos, entre los estadounidenses de 25 años o más que tuvieron títulos de doctorado en 2014, 37.1% son mujeres.
- Una pareja planea tener dos hijos. La probabilidad de que tengan dos chicas es del 25%.
- Javier elegirá un dígito al azar del 0 al 9. La probabilidad de que elija 3 es del 10%.
- Según el reporte meteorológico local, la probabilidad de tormentas eléctricas en la ciudad de Nueva York el 15 de julio es del 60%.
- Un club vende 50 boletos a una rifa. Osbaldo compró un boleto. La probabilidad de que gane el sorteo es del 2%.
Convertir decimales y fracciones a porcentajes
En los siguientes ejercicios, convertir cada decimal a un porcentaje.
- 0.01
- 0.03
- 0.18
- 0.15
- 1.35
- 1.56
- 3
- 4
- 0.009
- 0.008
- 0.0875
- 0.0625
- 1.5
- 2.2
- 2.254
- 2.317
En los siguientes ejercicios, convertir cada fracción a un porcentaje.
- \(\dfrac{1}{4}\)
- \(\dfrac{1}{5}\)
- \(\dfrac{3}{8}\)
- \(\dfrac{5}{8}\)
- \(\dfrac{7}{4}\)
- \(\dfrac{9}{8}\)
- \(6 \dfrac{4}{5}\)
- \(5 \dfrac{1}{4}\)
- \(\dfrac{5}{12}\)
- \(\dfrac{11}{12}\)
- \(2 \dfrac{2}{3}\)
- \(1 \dfrac{2}{3}\)
- \(\dfrac{3}{7}\)
- \(\dfrac{6}{7}\)
- \(\dfrac{5}{9}\)
- \(\dfrac{4}{9}\)
En los siguientes ejercicios, convertir cada fracción a un porcentaje.
- \(\dfrac{1}{4}\)de lavadoras necesitan reparación.
- \(\dfrac{1}{5}\)de los lavavajillas necesitan reparación.
En los siguientes ejercicios, convertir cada fracción a un porcentaje.
- Según el Centro Nacional de Estadísticas de Salud, en 2012, 7 20 de los adultos estadounidenses eran obesos.
- La Oficina del Censo de Estados Unidos estimó que en 2013, 85% de los estadounidenses vivían en la misma casa que 1 año antes.
En los siguientes ejercicios, completa la tabla.
-
Cuadro 6.26
| Fracción | Decimal | Por ciento |
|---|---|---|
| $$\ dfrac {1} {2} $$ | ||
| 0.45 | ||
| 18% | ||
| $$\ dfrac {1} {3} $$ | ||
| 0.0008 | ||
| 2 |
-
Cuadro 6.27
| Fracción | Decimal | Por ciento |
|---|---|---|
| $$\ dfrac {1} {4} $$ | ||
| 0.65 | ||
| 22% | ||
| $$\ dfrac {2} {3} $$ | ||
| 0.0004 | ||
| 3 |
Matemáticas cotidianas
- Impuesto a las ventas Felipa dice que tiene una manera fácil de estimar el impuesto a las ventas cuando realiza una compra. El impuesto a las ventas en su ciudad es del 9.05%. Ella sabe que esto es un poco menos del 10%.
- Convertir 10% a una fracción.
- Usa tu respuesta de (a) para estimar el impuesto a las ventas que Felipa pagaría con un vestido de $95.
- Savings Ryan tiene el 25% de cada cheque de pago automáticamente depositado en su cuenta de ahorros.
- Escribe el 25% como fracción.
- Usa tu respuesta de (a) para encontrar la cantidad que se destina al ahorro del cheque de pago de Ryan's $2,400.
- Amelio está comprando libros de texto en línea. Encontró tres vendedores que están ofreciendo un libro que necesita por el mismo precio, incluido el envío. Para decidir a qué vendedor comprar está comparando sus calificaciones de satisfacción del cliente. Las calificaciones se dan en el gráfico.
| Vendedor | Calificación |
|---|---|
| A | 4/5 |
| B | 3.5/4 |
| C | 85% |
- Escribe la calificación del vendedor C como fracción y decimal.
- Escribe la calificación del vendedor B como porcentaje y decimal.
- Escribe la calificación del vendedor A como porcentaje y decimal.
- ¿A qué vendedor debería comprarle Amelio y por qué?
Ejercicios de escritura
- Convierte 25%, 50%, 75% y 100% a fracciones. ¿Te das cuenta de un patrón? Explique cuál es el patrón.
- Convertir\(\dfrac{1}{10}, \dfrac{2}{10}, \dfrac{3}{10}, \dfrac{4}{10}, \dfrac{5}{10}, \dfrac{6}{10}, \dfrac{7}{10}, \dfrac{8}{10}\), y\(\dfrac{9}{10}\) a porcentajes. ¿Te das cuenta de un patrón? Explique cuál es el patrón.
- Cuando los Szetos vendieron su casa, el precio de venta era del 500% de lo que habían pagado por la casa hace 30 años. Explique lo que significa 500% en este contexto.
- Según cnn.com, el uso del celular en 2008 fue 600% de lo que había sido en 2001. Explique lo que significa 600% en este contexto.
Autocomprobación
(a) Después de completar los ejercicios, utilice esta lista de verificación para evaluar su dominio de los objetivos de esta sección.
(b) Si la mayoría de sus cheques fueron:
... con confianza. ¡Felicidades! Has logrado los objetivos en esta sección. Reflexiona sobre las habilidades de estudio que usaste para que puedas seguir usándolas. ¿Qué hiciste para confiar en tu capacidad para hacer estas cosas? Ser específico.
... con alguna ayuda. Esto debe abordarse rápidamente porque los temas que no dominas se convierten en baches en tu camino hacia el éxito. En matemáticas, cada tema se basa en trabajos anteriores. Es importante asegurarse de tener una base sólida antes de seguir adelante. ¿A quién puedes pedir ayuda? Tus compañeros de clase e instructor son buenos recursos. ¿Hay algún lugar en el campus donde estén disponibles los tutores de matemáticas? ¿Se pueden mejorar tus habilidades de estudio?
... no, ¡no lo comprendo! Esta es una señal de advertencia y no debes ignorarla. Debería obtener ayuda de inmediato o rápidamente se verá abrumado. Consulte a su instructor lo antes posible para discutir su situación. Juntos pueden idear un plan para obtener la ayuda que necesita.