1.1: Conjuntos de números reales y plano de coordenadas cartesianas

Juegos de Números

Si bien a los autores no les gustaría nada más que ahondar rápida y profundamente en la pura emoción que es el Precálculo, la experiencia ¹ nos ha enseñado que un breve repaso sobre algunas nociones básicas es bienvenido, si no del todo necesario, en esta etapa. Para ello, presentamos un breve resumen de la “teoría de conjuntos” y algunos de los vocabulario y anotaciones asociados que utilizamos en el texto. Como todos los buenos libros de Matemáticas, comenzamos con una definición.

Definición 1.1

Un conjunto es una colección bien definida de objetos que se llaman los 'elementos' del conjunto. Aquí, 'bien definido' significa que es posible determinar si algo pertenece o no a la colección, sin perjuicio.

Por ejemplo, la colección de letras que conforman la palabra “smolko” está bien definida y es un conjunto, pero la colección de los peores profesores de matemáticas del mundo no está bien definida, y por lo tanto no es un conjunto. ² En general, hay tres formas de describir conjuntos. Ellos son

Formas de describir conjuntos

1. El Método Verbal: Usa una oración para definir un conjunto.
2. El Método Roster: Comience con una llave izquierda '\(\{\)', enumere cada elemento del conjunto solo una vez y luego termine con una llave derecha '\(\}\)'.
3. El método Set-Builder: Una combinación de los métodos verbal y roster utilizando una “variable ficticia” como\(x\).

Por ejemplo, deja\(S\) ser el conjunto descrito verbalmente como el conjunto de letras que componen la palabra “smolko”. Una descripción de la lista de\(S\) sería\(\left\{ s, m, o, l, k \right\}\). Tenga en cuenta que enumeramos 'o' solo una vez, a pesar de que aparece dos veces en “smolko”. Además, el orden de los elementos no importa, por lo que también\(\left\{ k, l, m, o, s \right\}\) es una descripción de roster de\(S\). Una descripción del constructor de conjuntos\(S\) es:\[\{ x \, | \, \mbox{$x$ is a letter in the word ``smolko''.}\}\]

La manera de leer esto es: 'El conjunto de elementos\(x\)\(x\) es una letra en la palabra “smolko”. ' En cada uno de los casos anteriores, podemos usar el signo de igual familiar '\(=\)' y escribir\(S = \left\{ s, m, o, l, k \right\}\) o\(\ S=\{x \mid x \text { is a letter in the word "smolko". }\}\). Claramente\(m\) está\(S\) dentro y no\(q\) está en\(S\). Expresamos estos sentimientos matemáticamente por escrito\(m \in S\) y\(q \notin S\). A lo largo de tu educación matemática, te has encontrado con varios conjuntos famosos de números. A continuación se enumeran.

Juegos de Números

1. El conjunto vacío:\(\ \emptyset=\{\}=\{x \mid x \neq x\}\). Este es el conjunto sin elementos. Al igual que el número '\(0\),' juega un papel vital en las matemáticas. ^a
2. Los números naturales:\(\mathbb N= \{ 1, 2, 3, \ldots\}\) Los periodos de puntos suspensivos aquí indican que los números naturales contienen\(1\),,\(2\)\(3\), 'y así sucediente'.
3. Los números enteros:\(\mathbb W = \{ 0, 1, 2, \ldots \}\)
4. Los enteros:\(\mathbb Z=\{ \ldots, -3, -2, -1, 0, 1, 2, 3, \ldots \}\)
5. Los números racionales:\(\mathbb Q=\left\{\frac{a}{b} \, | \, a \in \mathbb Z \, \mbox{and} \, b \in \mathbb Z \right\}\). nales los números son los s de enteros (¡siempre que el denominador no sea cero!) Resulta que otra forma de describir los números racionales ^b es:\[\mathbb Q=\{x\,|\,\mbox{$x$ possesses a repeating or terminating decimal representation.}\}\]
6. Los números reales:\(\ \mathbb{R}=\{x \mid x \text { possesses a decimal representation. }\}\)
7. Los números irracionales:\(\ \mathbb{P}=\{x \mid x \text { is a non-rational real number. }\}\) Dicho de otra manera, un número racional es un decimal que ni repite ni termina. ^c
8. Los números complejos:\(\ \mathbb{C}=\{a+b i \mid a, b \in \mathbb{R} \text { and } i=\sqrt{-1}\}\) A pesar de su importancia, los números complejos juegan sólo un papel menor en el texto. ^d

---

^a. que, lamentablemente, no vamos a explorar en este texto.

^b Véase la Sección 9.2.

^c El ejemplo clásico es el número\(\ \pi\) (Ver Sección 10.1), pero números como\(\ \sqrt{2}\) y 0.101001000100001.. son otros representantes finos.

^d Aparecen primero en la Sección 3.4 y regresan en la Sección 11.7

Es importante señalar que cada número natural es un número entero, que, a su vez, es un número entero. Cada entero es un número racional (tomar\(b =1\) en la definición anterior para\(\mathbb Q\)) y los números racionales son todos números reales, ya que poseen representaciones decimales. ³ Si tomamos\(b=0\) en la definición anterior de\(\mathbb C\), vemos que cada número real es un número complejo. En este sentido, los conjuntos\(\mathbb N\),\(\mathbb W\),\(\mathbb Z\),\(\mathbb Q\),\(\mathbb R\), y\(\mathbb C\) se 'anidan' como muñecas Matryoshka.

En su mayor parte, este libro de texto se centra en conjuntos cuyos elementos provienen de los números reales\(\mathbb R\). Recordemos que podemos visualizar\(\mathbb R\) como una línea. Los segmentos de esta línea se denominan intervalos de números. A continuación se muestra un resumen de la denominada notación de intervalo asociada con conjuntos de números dados. Para intervalos con extremos finitos, enumeramos el punto final izquierdo, luego el extremo derecho. Usamos corchetes, '\([\)' o\(]\) '', si el punto final está incluido en el intervalo y usamos un punto rellenado o 'cerrado' para indicar pertenencia al intervalo. De lo contrario, usamos paréntesis,\((\) '' o\()\) '' y un círculo 'abierto' para indicar que el punto final no es parte del conjunto. Si el intervalo no tiene extremos finitos, utilizamos los símbolos\(-\infty\) para indicar que el intervalo se extiende indefinidamente hacia la izquierda y\(\infty\) para indicar que el intervalo se extiende indefinidamente hacia la derecha. Como infinito es un concepto, y no un número, siempre usamos paréntesis cuando usamos estos símbolos en notación de intervalo, y usamos una flecha apropiada para indicar que el intervalo se extiende indefinidamente en una (o ambas) direcciones.

Notación de intervalos

Dejar\(a\) y\(b\) ser números reales con\(a<b\).

Conjunto de números reales	Notación de intervalos	Región en la línea numérica real
\(\ \{x \mid a<x<b\}\)	\(\ (a, b)\)
\(\ \{x \mid a \leq x<b\}\)	\(\ [a, b)\)
\(\ \{x \mid a<x \leq b\}\)	\(\ (a, b]\)
\(\ \{x \mid a \leq x \leq b\}\)	\(\ [a, b]\)
\(\ \{x \mid x<b\}\)	\(\ (-\infty, b)\)
\(\ \{x \mid x \leq b\}\)	\(\ (-\infty, b]\)
\(\ \{x \mid x>a\}\)	\(\ (a, \infty)\)
\(\ \{x \mid x \geq a\}\)	\(\ [a, \infty)\)
\(\ \mathbb{R}\)	\(\ (-\infty, \infty)\)

Para un ejemplo, considere los conjuntos de números reales que se describen a continuación.

Conjunto de números reales	Notación de intervalos	Región en la línea numérica real
\(\ \{x \mid 1 \leq x<3\}\)	\(\ [1, 3)\)
\(\ \{x \mid-1 \leq x \leq 4\}\)	\(\ [−1, 4]\)
\(\ \{x \mid x \leq 5\}\)	\(\ (-\infty, 5]\)
\(\ \{x \mid x>-2\}\)	\(\ (-2, \infty)\)

A menudo tendremos ocasión de combinar conjuntos. Hay dos formas básicas de combinar conjuntos: intersección y unión. A continuación definimos ambos conceptos.

Definición 1.2

Supongamos\(A\) y\(B\) son dos conjuntos.

• La intersección de\(A\) y\(B\):\(A \cap B = \{ x \, | \, x \in A \, \text{and} \,\, x \in B \}\)
• La unión de\(A\) y\(B\):\(A \cup B = \{ x \, | \, x \in A \, \text{or} \,\, x \in B \, \, \text{(or both)} \}\)

Dicho de otra manera, la intersección de dos conjuntos es la superposición de los dos conjuntos, los elementos que los conjuntos tienen en común. La unión de dos conjuntos consiste en la totalidad de los elementos en cada uno de los conjuntos, recogidos juntos. ⁴ Por ejemplo, si\(A = \{ 1,2,3 \}\) y\(B = \{2,4,6 \}\), entonces\(A \cap B = \{2\}\) y\(A \cup B = \{1,2,3,4,6\}\). Si\(A = [-5,3)\) y\(B = (1, \infty)\), entonces podemos encontrar\(A \cap B\) y\(A\cup B\) gráficamente. Para encontrar\(A\cap B\), sombreamos el solapamiento de los dos y obtenemos\(A \cap B = (1,3)\). Para encontrar\(A \cup B\), sombreamos cada uno de\(A\)\(B\) y describimos la región sombreada resultante para encontrar\(A \cup B = [-5,\infty)\).

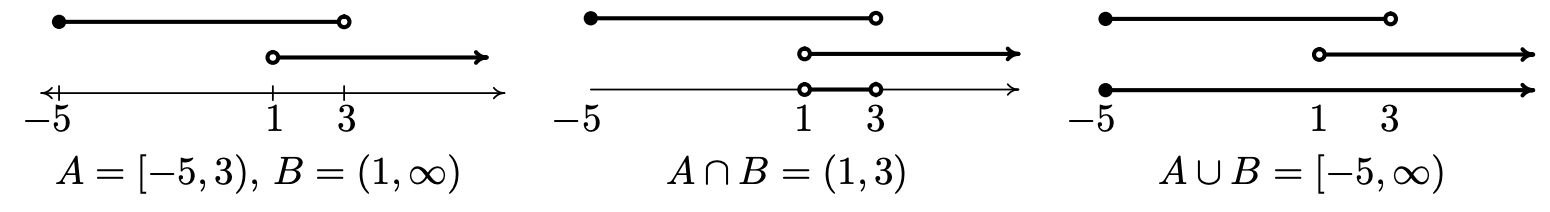
Si bien tanto la intersección como la unión son importantes, tenemos más ocasión de usar unión en este texto que intersección, simplemente porque la mayoría de los conjuntos de números reales con los que estaremos trabajando son intervalos o son uniones de intervalos, como ilustra el siguiente ejemplo.

Ejemplo 1.1.1

Exprese los siguientes conjuntos de números usando notación de intervalo.

1. \(\ \{x \mid x \leq-2 \text { or } x \geq 2\}\)
2. \(\ \{x \mid x \neq 3\}\)
3. \(\ \{x \mid x \neq \pm 3\}\)
4. \(\ \{x \mid-1<x \leq 3 \text { or } x=5\}\)

Solución

1. La mejor manera de proceder aquí es graficar el conjunto de números en la recta numérica y obtener la respuesta de ella. La desigualdad\(x \leq -2\) corresponde al intervalo\((-\infty, -2]\) y la desigualdad\(x \geq 2\) corresponde al intervalo\([2, \infty)\). Ya que estamos buscando describir los números reales\(x\) en uno de estos u otros, tenemos\(\{ x \, | \, x \leq -2 \, \, \text{or} \, \, x \geq 2 \} = (-\infty, -2] \cup [2, \infty)\).

   

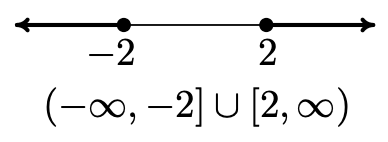
2. Para el conjunto\(\{ x \, | \, x \neq 3 \}\), sombreamos toda la línea numérica real excepto\(x=3\), donde dejamos un círculo abierto. Esto divide la recta numérica real en dos intervalos,\((-\infty, 3)\) y\((3,\infty)\). Dado que los valores de\(x\) podrían estar en uno de estos intervalos o en el otro, tenemos que\(\{ x \, | \, x \neq 3 \} = (-\infty, 3) \cup (3,\infty)\)

   

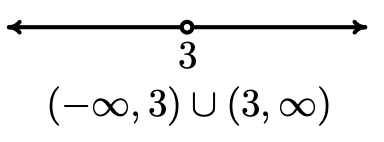
3. Para el conjunto\(\{ x \, | \, x \neq \pm 3 \}\), procedemos como antes y excluimos ambos\(x=3\) y\(x=-3\) de nuestro conjunto. Esto divide la recta numérica en tres intervalos,\((-\infty, -3)\),\((-3,3)\) y\((3, \infty)\). Dado que el conjunto describe números reales que provienen del primer, segundo o tercer intervalo, tenemos\(\{ x \, | \, x \neq \pm 3 \} = (-\infty, -3) \cup (-3,3) \cup (3, \infty)\).

   

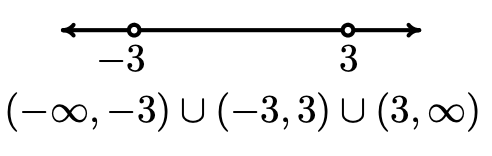
4. Graficando el conjunto\(\{ x \, | \, -1 < x \leq 3 \,\, \text{or} \,\, x = 5\}\), obtenemos un intervalo,\((-1,3]\) junto con un solo número, o punto,\(\{ 5\}\). Si bien podríamos expresar esto último como\([5,5]\) (¿Ves por qué?) , elegimos escribir nuestra respuesta como\(\{ x \, | \, -1 < x \leq 3 \,\, \text{or} \,\, x = 5\} = (-1,3] \cup \{ 5\}\).

   

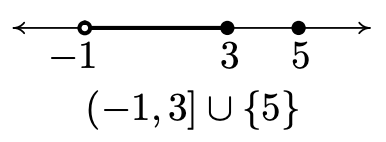
El plano de coordenadas cartesianas

Para visualizar la pura emoción que es el Precálculo, necesitamos unir Álgebra y Geometría. En pocas palabras, debemos encontrar la manera de dibujar cosas algebraicas. Empecemos por posiblemente el mayor logro matemático de todos los tiempos: el Plano de Coordenadas Cartesianas. ⁵ Imagine dos líneas numéricas reales cruzando en ángulo recto\(0\) como se dibuja a continuación.

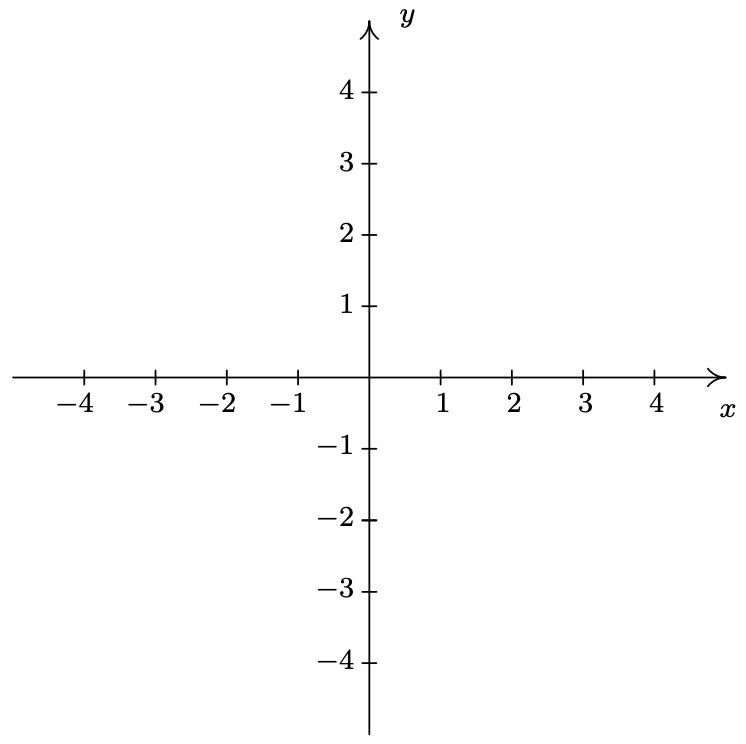
La línea numérica horizontal generalmente se denomina \(x\)eje -mientras que la línea numérica vertical se suele llamar \(y\)eje -eje. ⁶ Al igual que con la línea numérica habitual, imaginamos que estos ejes se extienden indefinidamente en ambas direcciones. ⁷ Tener dos líneas numéricas nos permite ubicar las posiciones de los puntos fuera de las líneas numéricas así como los puntos en las propias líneas.

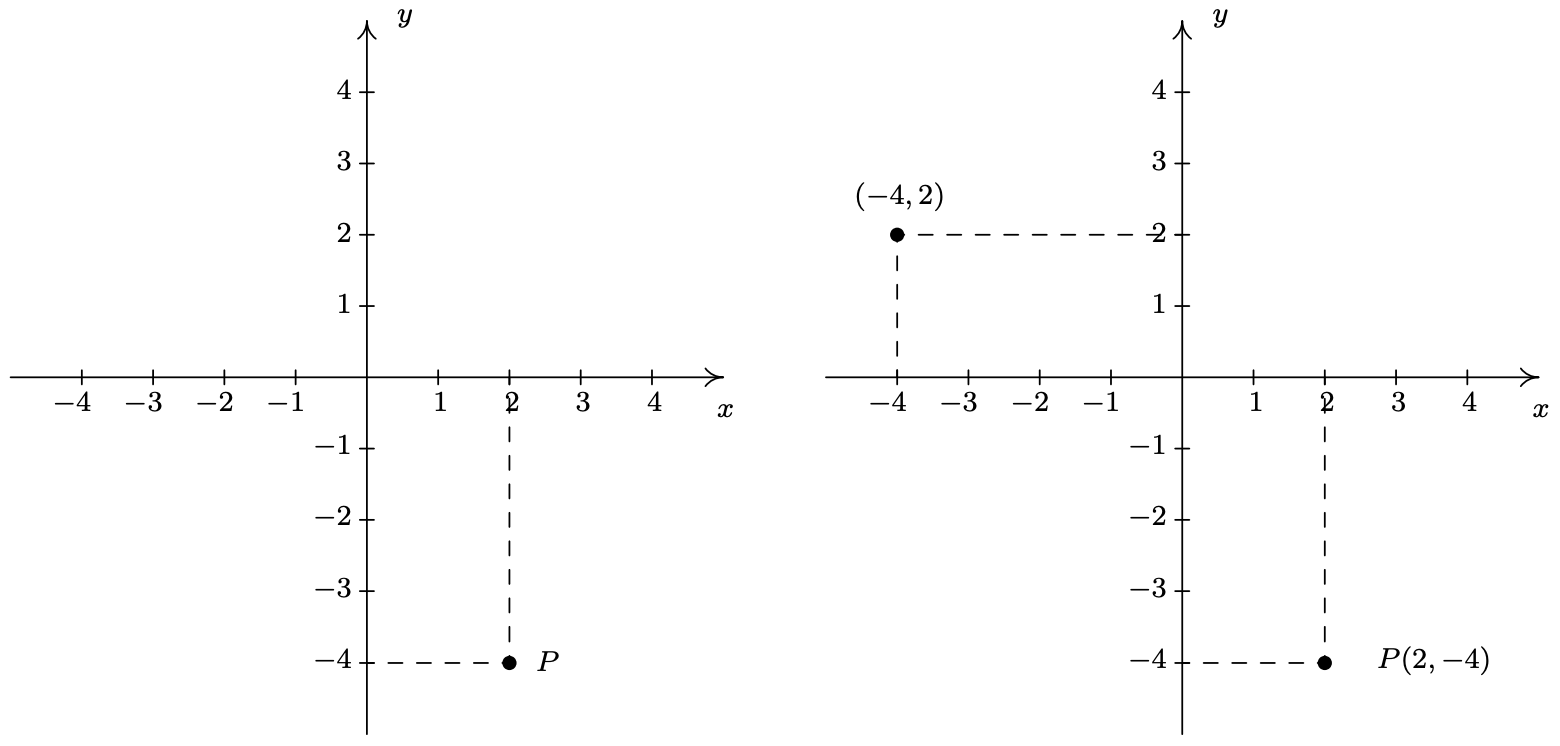
Por ejemplo, considere el punto\(P\) en la página siguiente. Para usar los números en los ejes para etiquetar este punto, imaginamos dejar caer una línea vertical desde el\(x\) eje -hasta\(P\) y extendiendo una línea horizontal desde el\(y\) eje -hasta\(P\). A este proceso se le llama a veces 'proyectar' el punto\(P\) al eje\(x\) - (respectivamente\(y\) -). Luego describimos el punto\(P\) usando el par ordenado\((2,-4)\). El primer número del par ordenado se llama abscisa o \(x\)coordenada y el segundo se llama la ordenada o \(y\)coordenada. ⁸ Tomados en conjunto, el par ordenado\((2,-4)\) comprende las coordenadas cartesianas ⁹ del punto\(P\). En la práctica, la distinción entre un punto y sus coordenadas es borrosa; por ejemplo, a menudo hablamos de 'el punto'\((2,-4)\). Podemos pensar en\((2,-4)\) como instrucciones sobre cómo llegar\(P\) desde el\((0, 0)\) moviendo\(2\) unidades hacia la derecha y\(4\) unidades hacia abajo. Observe que el orden en el par es importante\(-\) si deseamos trazar el punto\((-4,2)\), nos moveríamos a las\(4\) unidades de la izquierda desde el origen y luego moveríamos hacia arriba\(2\) unidades, como abajo a la derecha.

Cuando hablamos del Plano Coordenado Cartesiano, nos referimos al conjunto de todos los pares ordenados posibles\((x,y)\) como\(x\) y\(y\) tomamos valores de los números reales. A continuación se muestra un resumen de hechos importantes sobre las coordenadas cartesianas.

Datos importantes sobre el plano de coordenadas cartesianas

• \((a,b)\)y\((c,d)\) representan el mismo punto en el plano si y sólo si\(a = c\) y\(b = d\).
• \((x,y)\)yace en el\(x\) eje -si y solo si\(y = 0\).
• \((x,y)\)yace en el\(y\) eje -si y solo si\(x=0\).
• El origen es el punto\((0,0)\). Es el único punto común a ambos ejes.

Ejemplo 1.1.2

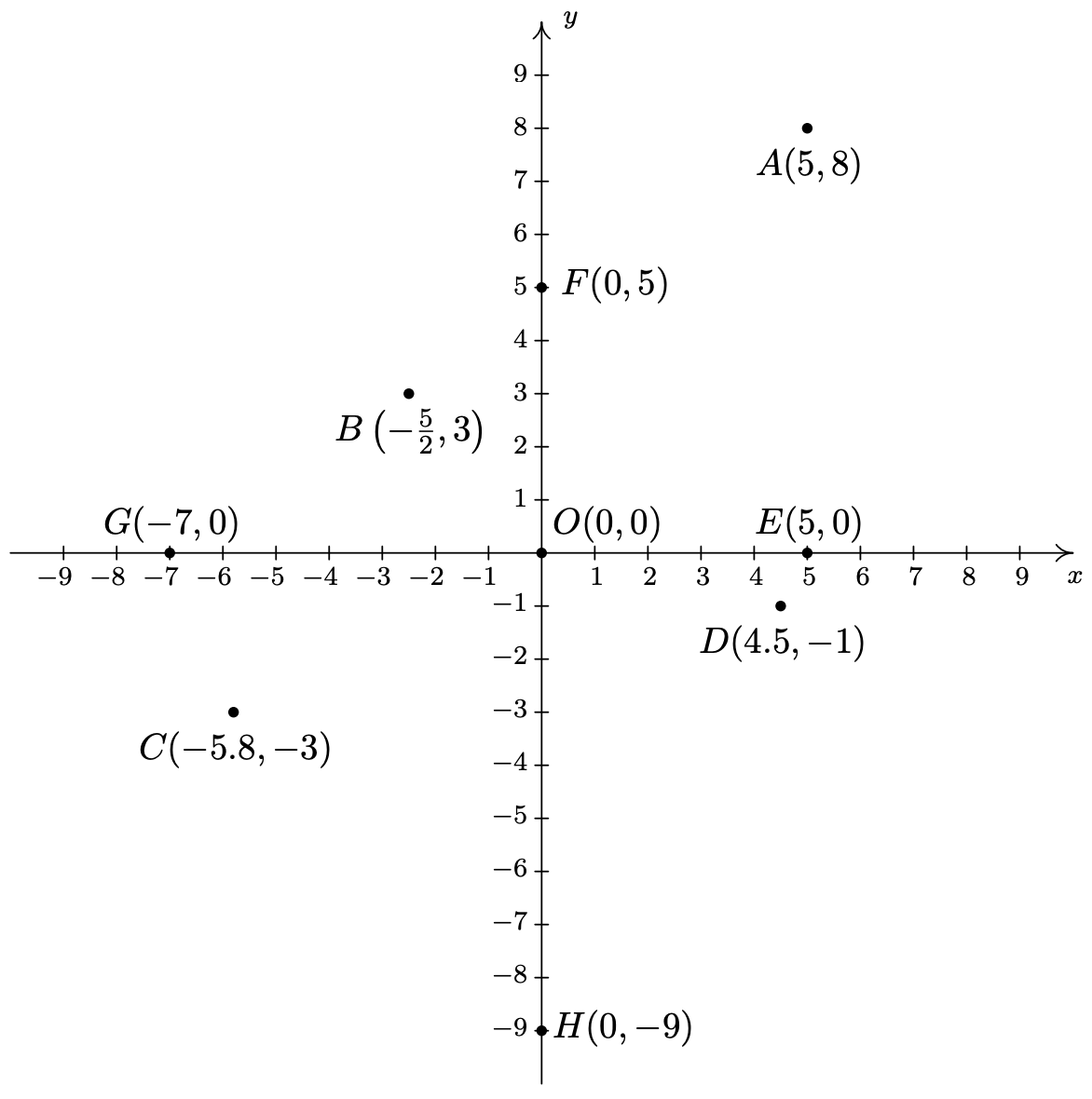
Trazar los siguientes puntos:\(A(5,8)\)\(B\left(-\frac{5}{2}, 3\right)\),,\(C(-5.8, -3)\),\(D(4.5, -1)\),\(E(5,0)\),\(F(0,5)\),\(G(-7,0)\),\(H(0, -9)\),\(O(0,0)\). ¹⁰

Solución

Para trazar estos puntos, partimos en el origen y nos movemos hacia la derecha si la\(x\) coordenada -es positiva; a la izquierda si es negativa. A continuación, nos movemos hacia arriba si la\(y\) coordenada -es positiva o hacia abajo si es negativa. Si la\(x\) coordenada -es\(0\), partimos en el origen y nos movemos a lo largo del\(y\) eje -solamente. Si la\(y\) coordenada -es\(0\) nos movemos a lo largo del\(x\) eje -solamente.

Los ejes dividen el plano en cuatro regiones llamadas cuadrantes. Están etiquetados con números romanos y avanzan en sentido antihorario alrededor del plano

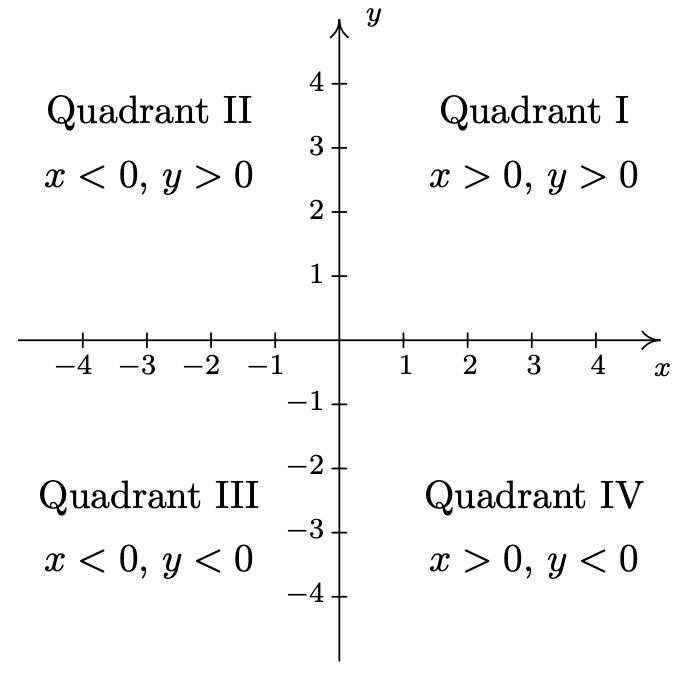
Por ejemplo,\((1,2)\) se encuentra en el Cuadrante I,\((-1,2)\) en el Cuadrante II,\((-1,-2)\) en el Cuadrante III y\((1,-2)\) en el Cuadrante IV. Si un punto distinto del origen pasa a estar sobre los ejes, normalmente nos referimos a ese punto como que se encuentra en el\(x\) eje positivo o negativo (if\(y = 0\)) o en el\(y\) eje positivo o negativo (if\(x = 0\)). Por ejemplo,\((0,4)\) se encuentra en el\(y\) eje positivo mientras que\((-117,0)\) se encuentra en el\(x\) eje negativo. Dichos puntos no pertenecen a ninguno de los cuatro cuadrantes.

Uno de los conceptos más importantes en todas las matemáticas es la simetría. ¹¹ Hay muchos tipos de simetría en Matemáticas, pero tres de ellos se pueden discutir fácilmente usando Coordenadas Cartesianas.

Definición 1.3

Dos puntos\((a,b)\) y\((c,d)\) en el avión se dice que son

• simétrico sobre el\(x\) eje -si\(a = c\) y\(b = -d\)
• simétrico sobre el\(y\) eje -si\(a = -c\) y\(b = d\)
• simétrico sobre el origen si\(a = -c\) y\(b = -d\)

Esquemáticamente,

En la figura anterior,\(P\) y\(S\) son simétricos alrededor del\(x\) eje -eje, como son\(Q\) y\(R\);\(P\) y\(Q\) son simétricos alrededor del\(y\) -eje, como son\(R\) y\(S\);\(P\) y\(R\) son simétricos sobre el origen, como son \(Q\)y\(S\).

Ejemplo 1.1.3

Que\(P\) sea el punto\((-2,3)\). Encuentra los puntos que son simétricos con\(P\) respecto a los:

1. \(x\)-eje
2. \(y\)-eje
3. origen

Comprueba tu respuesta trazando los puntos.

Solución

La figura después de la Definición 1.3 nos da una buena manera de pensar en encontrar puntos simétricos en términos de tomar los opuestos de las\(x\) -y/o\(y\) -coordenadas de\(P(-2,3)\).

1. Para encontrar el punto simétrico alrededor del\(x\) eje -eje, reemplazamos la\(y\) coordenada -con su opuesto para obtener\((-2,-3)\).
2. Para encontrar el punto simétrico alrededor del\(y\) eje -eje, reemplazamos la\(x\) coordenada -con su opuesto para obtener\((2,3)\).
3. Para encontrar el punto simétrico sobre el origen, reemplazamos las\(y\) coordenadas\(x\) - y -con sus opuestos para obtener\((2,-3)\).

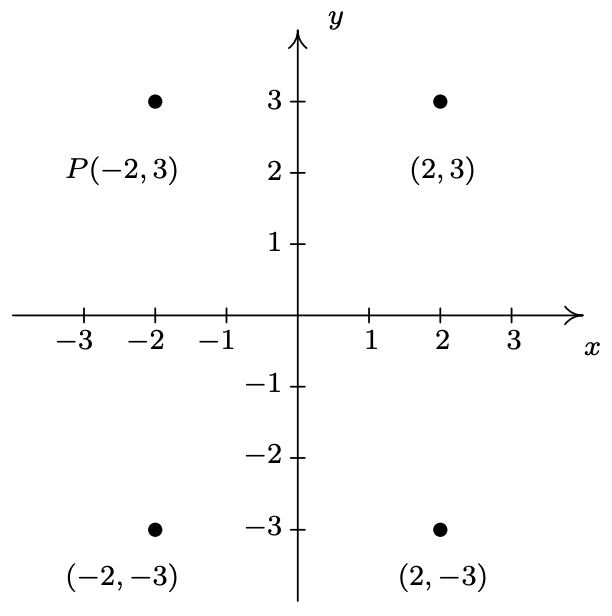
Una forma de visualizar los procesos en el ejemplo anterior es con el concepto de una reflexión. Si empezamos con nuestro punto\((-2,3)\) y pretendemos que el\(x\) -eje es un espejo, entonces el reflejo de\((-2,3)\) a través del\(x\) eje estaría en\((-2,-3)\). Si pretendemos que el\(y\) -eje es un espejo, el reflejo de\((-2,3)\) a través de ese eje sería\((2,3)\). Si reflexionamos a través del\(x\) eje\(y\) -y luego el -eje, íbamos de\((-2,3)\) a\((-2,-3)\) entonces a\((2,-3)\), y así terminaríamos en el punto simétrico a\((-2,3)\) aproximadamente el origen. Resumimos y generalizamos este proceso a continuación.

Reflexiones

Reflexionar un punto\((x,y)\) sobre:

• \(x\)-eje, reemplace\(y\) con\(-y\).
• \(y\)-eje, reemplace\(x\) con\(-x\).
• origen, sustituir por\(-x\) y\(x\)\(y\) con\(-y\).

Distancia en el Plano

Otro concepto importante en Geometría es la noción de longitud. Si vamos a unir Álgebra y Geometría usando el Plano Cartesiano, entonces necesitamos desarrollar una comprensión algebraica de lo que significa distancia en el plano. Supongamos que tenemos dos puntos,\(P\left(x_0, y_0\right)\) y\(Q\left(x_{1}, y_{1}\right),\) en el plano. Por la distancia\(d\) entre\(P\) y\(Q\), nos referimos a la longitud del segmento de línea que se une\(P\) con\(Q\). (Recuerde, dados dos puntos distintos en el plano, hay una línea única que contiene ambos puntos). Nuestro objetivo ahora es crear una fórmula algebraica para calcular la distancia entre estos dos puntos. Considera la situación genérica abajo a la izquierda.

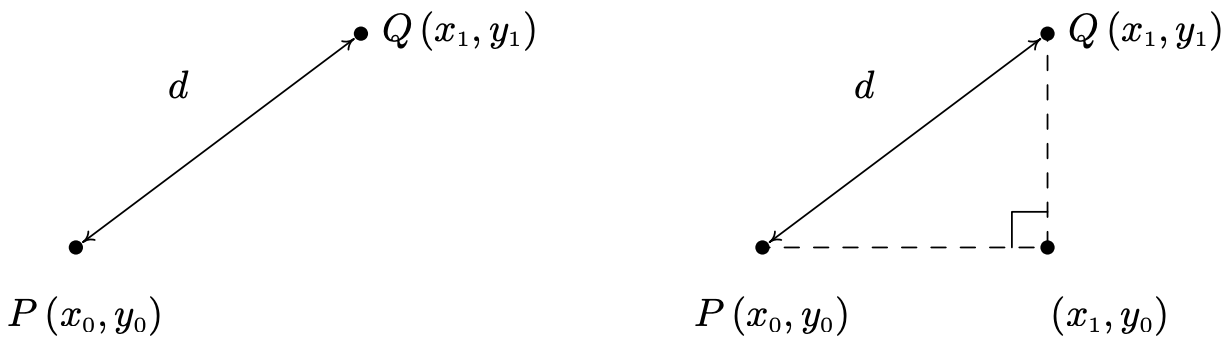
Con un poco más de imaginación, podemos imaginar un triángulo rectángulo cuya hipotenusa tiene longitud\(d\) tal como se dibuja arriba a la derecha. De esta última figura, vemos que las longitudes de las patas del triángulo son\(\left|x_{1} - x_0\right|\) y\(\left|y_{1} - y_0\right|\) así nos da el Teorema de Pitágoras

\[\left|x_1 - x_0\right|^2 + \left|y_1 - y_0\right|^2 = d^2\]\[\left(x_1 - x_0\right)^2 + \left(y_1 - y_0\right)^2 = d^2\]

(¿Recuerdas por qué podemos reemplazar la notación de valor absoluto con paréntesis?) Al extraer la raíz cuadrada de ambos lados de la segunda ecuación y usar el hecho de que la distancia nunca es negativa, obtenemos

Ecuación 1.1

La Fórmula de Distancia: La distancia\(d\) entre los puntos\(P\left(x_0, y_0\right)\) y\(Q\left(x_{1}, y_{1}\right)\) es:

\[d = \sqrt{ \left(x_1 - x_0\right)^2 + \left(y_1 - y_0\right)^2}\]

No siempre es así que los puntos\(P\) y se\(Q\) prestan a construir tal triángulo. Si los puntos\(P\) y\(Q\) están dispuestos vertical u horizontalmente, o describen exactamente el mismo punto, no podemos usar el argumento geométrico anterior para derivar la fórmula de distancia. Se deja al lector en el Ejercicio 35 verificar la Ecuación 1.1 para estos casos.

Ejemplo 1.1.4

Encuentre y simplifique la distancia entre\(P(-2,3)\) y\(Q(1,-3)\).

Solución

\[\begin{array}{rcl} d & = & \sqrt{\left(x_1 - x_0 \right)^2 + \left(y_1 - y_0 \right)^2} \\ & = & \sqrt{ (1-(-2))^2 + (-3-3)^2} \\ & = & \sqrt{9 + 36} \\ & = & 3 \sqrt{5} \end{array}\]

Entonces la distancia es\(3 \sqrt{5}\).

Ejemplo 1.1.5

Encuentra todos los puntos con\(x\) -coordenada\(1\) que son\(4\) unidades del punto\((3,2)\).

Solución

Pronto veremos que los puntos que deseamos encontrar están en la línea\(x=1\), pero por ahora sólo los veremos como puntos de la forma\((1,y)\). Visualmente,

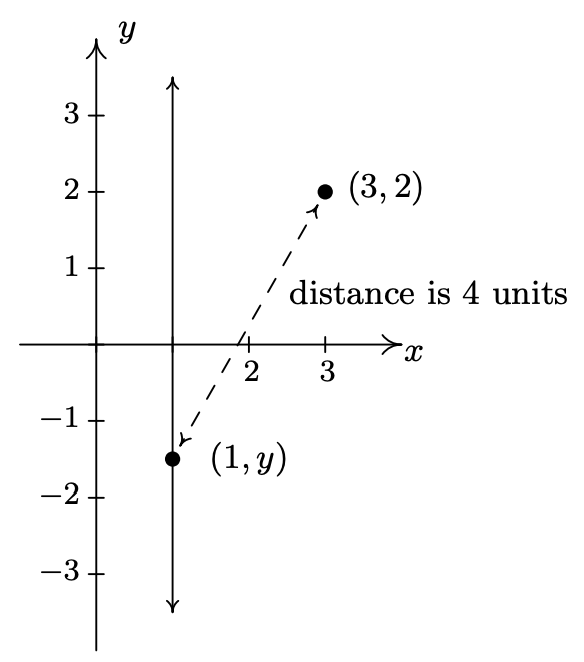
Requerimos que la distancia\((3,2)\) de\((1,y)\) estar\(4\). La Fórmula de Distancia, Ecuación 1.1, rinde

\[\begin{array}{rclr} d & = & \sqrt{\left(x_1-x_0\right)^2+\left(y_1-y_0\right)^2} & \\ 4 & = & \sqrt{(1-3)^2+(y-2)^2} & \\ 4 & = & \sqrt{4+(y-2)^2} & \\ 4^2 & = & \left(\sqrt{4+(y-2)^2}\right)^2 & \mbox{squaring both sides} \\ 16 & = & 4+(y-2)^2 & \\ 12 & = & (y-2)^2 & \\ (y-2)^2 & = & 12 & \\ y - 2 & = & \pm \sqrt{12} & \mbox{extracting the square root} \\ y-2 & = & \pm 2 \sqrt{3} & \\ y & = & 2 \pm 2 \sqrt{3} & \end{array}\]

Obtenemos dos respuestas:\((1, 2 + 2 \sqrt{3})\) y Se anima\((1, 2-2 \sqrt{3}).\) al lector a pensar por qué hay dos respuestas.

Relacionado con encontrar la distancia entre dos puntos está el problema de encontrar el punto medio del segmento de línea que conecta dos puntos. Dados dos puntos,\(P\left(x_0, y_0\right)\) y\(Q\left(x_{1}, y_{1}\right)\), el punto medio\(M\) de\(P\) y\(Q\) se define como el punto en el segmento de línea que se conecta\(P\) y\(Q\) cuya distancia desde\(P\) es igual a su distancia desde\(Q\).

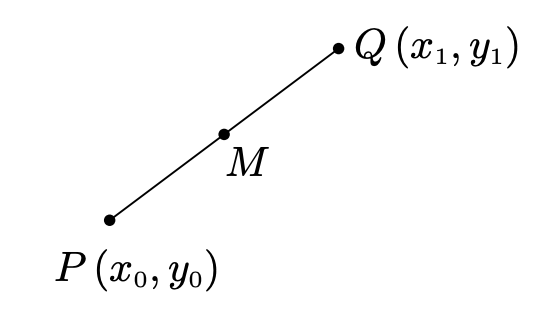
Si pensamos en llegar\(M\) yendo 'a mitad de camino' y 'a mitad arriba' obtenemos la siguiente fórmula.

Ecuación 1.2

La fórmula del punto medio: El punto medio\(M\) del segmento de línea que conecta\(P\left(x_0, y_0\right)\) y\(Q\left(x_{1}, y_{1}\right)\) es:

\[M = \left( \dfrac{x_0 + x_1}{2} , \dfrac{y_0 + y_1}{2} \right)\]

Si dejamos\(d\) denotar la distancia entre\(P\) y\(Q\), la dejamos como Ejercicio 36 para mostrar que la distancia entre\(P\) y\(M\) es la misma\(d/2\) que la distancia entre\(M\) y\(Q\). Esto basta para mostrar que la Ecuación 1.2 da las coordenadas del punto medio.

Ejemplo 1.1.6

Encuentre el punto medio del segmento de línea que conecta\(P(-2,3)\) y\(Q(1,-3)\).

Solución

\[\begin{array}{rcl} M & = & \left( \dfrac{x_0+x_1}{2}, \dfrac{y_0+y_1}{2} \right) \\ & = & \left( \dfrac{(-2)+1}{2}, \dfrac{3+(-3)}{2} \right) = \left(- \dfrac{1}{2}, \dfrac{0}{2} \right) \\ & = & \left(- \dfrac{1}{2}, 0 \right) \end{array}\]

El punto medio es\(\left(- \frac{1}{2}, 0 \right)\).

Cerramos con una aplicación más abstracta de la Fórmula de Punto Medio. Revisaremos el siguiente ejemplo en el Ejercicio 72 en la Sección 2.1.

Ejemplo 1.1.7

Si\(a \neq b\), probar que la línea divide\(y = x\) por igual el segmento de línea con puntos finales\((a,b)\) y\((b,a)\).

Solución. Para probar la afirmación, utilizamos la Ecuación 1.2 para encontrar el punto medio

\[\begin{array}{rcl} M & = & \left( \dfrac{a+b}{2}, \dfrac{b+a}{2} \right) \\ & = & \left( \dfrac{a+b}{2}, \dfrac{a+b}{2} \right) \\ \end{array}\]

Dado que las\(y\) coordenadas\(x\) y de este punto son las mismas, encontramos que el punto medio se encuentra en la línea\(y=x\), según se requiera.

Ejercicios

1. Rellena el cuadro a continuación:

   Conjunto de números reales	Notación de intervalos	Región en la línea numérica real
   \(\ \{x \mid-1 \leq x<5\}\)
   	\(\ [0, 3)\)
   \(\ \{x \mid-5<x \leq 0\}\)
   	\(\ (−3, 3)\)
   \(\ \{x \mid x \leq 3\}\)
   	\(\ (-\infty, 9)\)
   \(\ \{x \mid x \geq-3\}\)

En los Ejercicios 2 -7, encuentre la intersección o unión indicada y simplifique si es posible. Exprese sus respuestas en notación de intervalos.

2. \((-1,5] \cap [0,8)\)[findunionintfirst]
3. \((-1,1) \cup [0,6]\)
4. \((-\infty,4]\cap (0,\infty)\)
5. \((-\infty,0) \cap [1,5]\)
6. \((-\infty, 0) \cup [1,5]\)
7. \((-\infty, 5] \cap [5,8)\)[findunionintlast]

En Ejercicios 8 - 9, escribe el conjunto usando notación de intervalos.

8. \(\{x\,|\, x \neq 5 \}\)[writeintervalfirst]
9. \(\{x\,|\, x \neq -1 \}\)
10. \(\{x\,|\, x \neq -3,\, 4 \}\)
11. \(\{x\,|\, x \neq 0, \, 2 \}\)
12. \(\{x\,|\, x \neq 2, \, -2 \}\)
13. \(\{x\,|\, x \neq 0,\, \pm 4 \}\)
14. \(\{x\,|\, x \leq -1 \, \text{or} \, x \geq 1 \}\)
15. \(\{x\,|\, x < 3 \, \text{or} \, x \geq 2 \}\)
16. \(\{x\,|\, x \leq -3 \, \text{or} \, x > 0 \}\)
17. \(\{x\,|\, x \leq 5 \, \text{or} \, x = 6 \}\)
18. \(\{x\,|\, x > 2 \, \text{or} \, x = \pm 1 \}\)
19. \(\{x\,|\, -3 < x < 3 \, \text{or} \, x = 4 \}\)[writeintervallast]
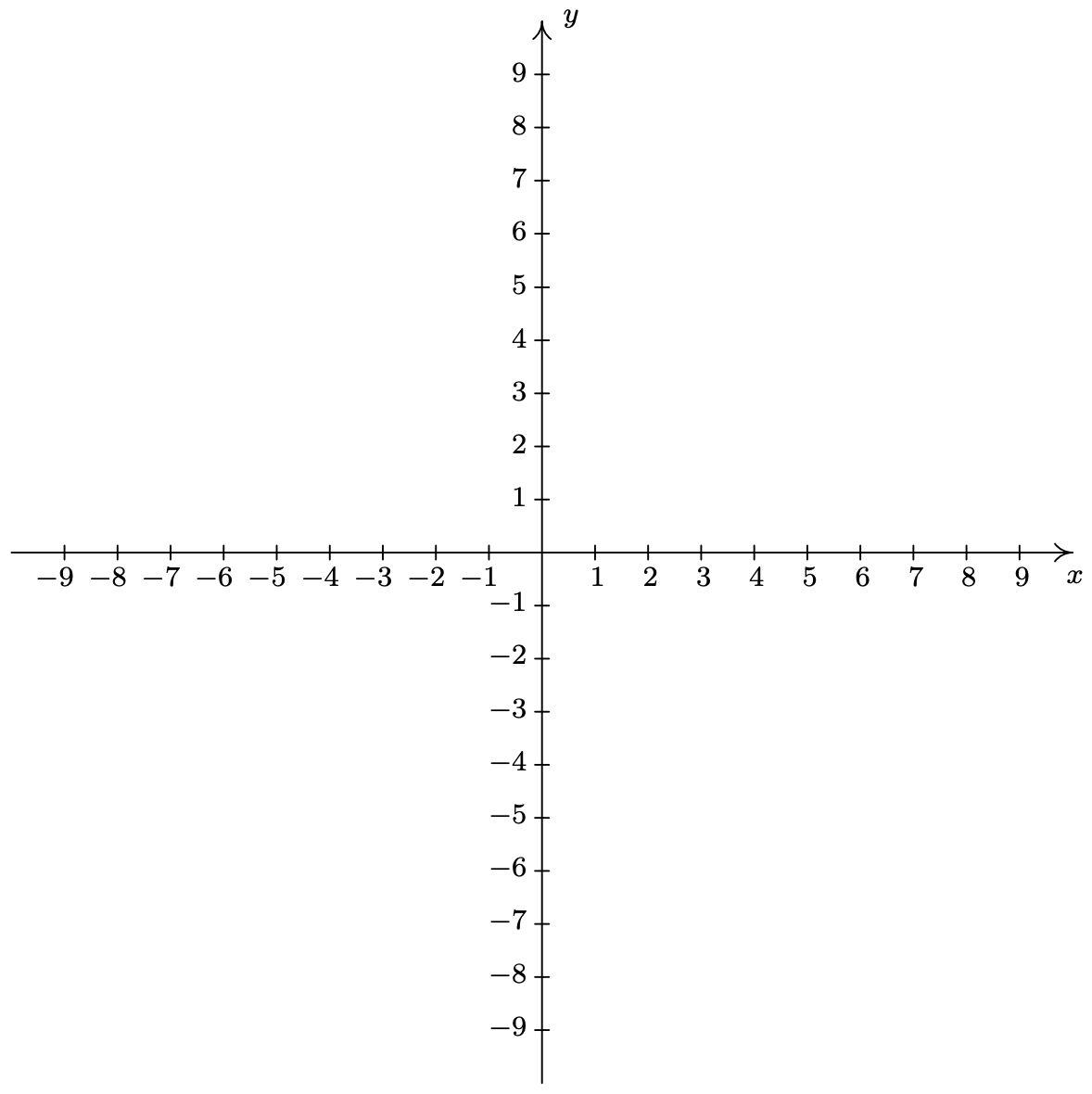
20. Trace y etiquete los puntos\(\;A(-3, -7)\),\(\;B(1.3, -2)\),\(\;C(\pi, \sqrt{10})\),\(\;D(0, 8)\),\(\;E(-5.5, 0)\)\(\;F(-8, 4)\),\(\;G(9.2, -7.8)\) y\(H(7, 5)\) en el Plano de Coordenadas Cartesianas que se indica a continuación.

21. Por cada punto dado en el Ejercicio 20 anterior
    • Identificar el cuadrante o eje en/sobre el que se encuentra el punto.
    • Encuentra el punto simétrico al punto dado alrededor del\(x\) eje.
    • Encuentra el punto simétrico al punto dado alrededor del\(y\) eje.
    • Encuentra el punto simétrico al punto dado sobre el origen.

En los Ejercicios 22 - 29, encuentra la distancia\(d\) entre los puntos y el punto medio\(M\) del segmento de línea que los conecta.

22. \((1,2)\),\((-3,5)\) [distmidfirst]
23. \((3, -10)\),\((-1, 2)\)
24. \(\left( \dfrac{1}{2}, 4\right)\),\(\left(\dfrac{3}{2}, -1\right)\)
25. \(\left(- \dfrac{2}{3}, \dfrac{3}{2} \right)\),\(\left(\dfrac{7}{3}, 2\right)\)
26. \(\left( \dfrac{24}{5}, \dfrac{6}{5} \right)\),\(\left( -\dfrac{11}{5}, -\dfrac{19}{5} \right)\).
27. \(\left(\sqrt{2}, \sqrt{3}\right)\),\(\left(-\sqrt{8}, -\sqrt{12}\right)\)
28. \(\left(2 \sqrt{45}, \sqrt{12} \right)\),\(\left(\sqrt{20}, \sqrt{27} \right)\).
29. \((0, 0)\),\((x, y)\) [distmidlast]
30. Encuentra todos los puntos del formulario\((x, -1)\) que son\(4\) unidades desde el punto\((3,2)\).
31. Encuentra todos los puntos en el\(y\) eje -que son\(5\) unidades desde el punto\((-5,3)\).
32. Encuentra todos los puntos en el\(x\) eje -que son\(2\) unidades desde el punto\((-1,1)\).
33. Encuentra todos los puntos del formulario\((x,-x)\) que son\(1\) unidades desde el origen.
34. Supongamos por un momento que estamos parados en el origen y los puntos positivos\(y\) del eje debido al Norte mientras que el\(x\) eje positivo apunta a Oriente. Nuestro Sasquatch-o-meter nos dice que Sasquatch está a 3 millas al oeste y 4 millas al sur de nuestra posición actual. ¿Cuáles son las coordenadas de su posición? ¿A qué distancia está él de nosotros? Si corre 7 millas con rumbo Este ¿cuál sería su nueva posición?
35. Verifique la Fórmula de Distancia 1.1 para los casos en los que:
    1. Los puntos están dispuestos verticalmente. (Pista: Uso\(P(a, y_0)\) y\(Q(a, y_{1})\).)
    2. Los puntos están dispuestos horizontalmente. (Pista: Uso\(P(x_0, b)\) y\(Q(x_{1}, b)\).)
    3. Los puntos son en realidad el mismo punto. (No deberías necesitar una pista para este.)
36. Verifique la Fórmula de punto medio mostrando la distancia entre\(P(x_{1}, y_{1})\) y\(M\) y la distancia entre\(M\) y\(Q(x_{2}, y_{2})\) son ambos la mitad de la distancia entre\(P\) y\(Q\).
37. Mostrar que los puntos\(A\),\(\;B\) y\(C\) abajo son los vértices de un triángulo rectángulo.
    1. \(A(-3,2)\),\(\;B(-6,4)\), y\(C(1,8)\)
    2. \(A(-3, 1)\),\(\;B(4, 0)\) y\(C(0, -3)\)
38. Encuentra un punto\(D(x, y)\) tal que los puntos\(A(-3, 1)\),\(\;B(4, 0)\),\(\;C(0, -3)\) y\(D\) son las esquinas de un cuadrado. Justifica tu respuesta.
39. Discuta con sus compañeros de clase cuántos números hay en el intervalo\((0,1)\).
40. [ordenadotripleejercicio] El mundo no es plano. ¹² Así, el Plano Cartesiano no puede ser posiblemente el final de la historia. Discuta con sus compañeros de clase cómo extendería las Coordenadas Cartesianas para representar el mundo tridimensional. ¿Cómo serían las fórmulas Distancia y Punto Medio, asumiendo que esos conceptos tienen sentido en absoluto?

RESPUESTAS

1. Conjunto de números reales	Notación de intervalos	Región en la línea numérica real
   \(\ \{x \mid-1 \leq x<5\}\)	\(\ [−1, 5)\)
   \(\ \{x \mid 0 \leq x<3\}\)	\(\ [0, 3)\)
   \(\ \{x \mid 2<x \leq 7\}\)	\(\ (2, 7]\)
   \(\ \{x \mid-5<x \leq 0\}\)	\(\ (−5, 0]\)
   \(\ \{x \mid-3<x<3\}\)	\(\ (−3, 3)\)
   \(\ \{x \mid 5 \leq x \leq 7\}\)	\(\ [5, 7]\)
   \(\ \{x \mid x \leq 3\}\)	\(\ (-\infty, 3]\)
   \(\ \{x \mid x<9\}\)	\(\ (-\infty, 9)\)
   \(\ \{x \mid x>4\}\)	\(\ (4, \infty)\)
   \(\ \{x \mid x \geq-3\}\)	\(\ [-3, \infty)\)

2. \((-1,5] \cap [0,8) = [0,5]\)
3. \((-1,1) \cup [0,6] = (-1,6]\)
4. \((-\infty,4]\cap (0,\infty) = (0,4]\)
5. \((-\infty,0) \cap [1,5] = \emptyset\)
6. \((-\infty, 0) \cup [1,5] = (-\infty,0) \cup [1,5]\)
7. \((-\infty, 5] \cap [5,8) = \left\{ 5\right\}\)
8. \((-\infty, 5) \cup (5, \infty)\)
9. \((-\infty, -1) \cup (-1, \infty)\)
10. \((-\infty, -3) \cup (-3, 4)\cup (4, \infty)\)
11. \((-\infty, 0) \cup (0, 2)\cup (2, \infty)\)
12. \((-\infty, -2) \cup (-2, 2)\cup (2, \infty)\)
13. \((-\infty, -4) \cup (-4, 0) \cup (0, 4) \cup (4, \infty)\)
14. \((-\infty, -1] \cup [1, \infty)\)
15. \((-\infty, \infty)\)
16. \((-\infty, -3] \cup (0, \infty)\)
17. \((-\infty, 5] \cup \{6\}\)
18. \(\{-1\} \cup \{1\} \cup (2, \infty)\)
19. \((-3,3) \cup \{4\}\)
20. Los puntos requeridos\(\;A(-3, -7)\),\(\;B(1.3, -2)\),\(\;C(\pi, \sqrt{10})\),,\(\;D(0, 8)\),\(\;E(-5.5, 0)\)\(\;F(-8, 4)\)\(\;G(9.2, -7.8)\), y\(H(7, 5)\) se trazan en el Plano de Coordenadas Cartesianas a continuación.

    

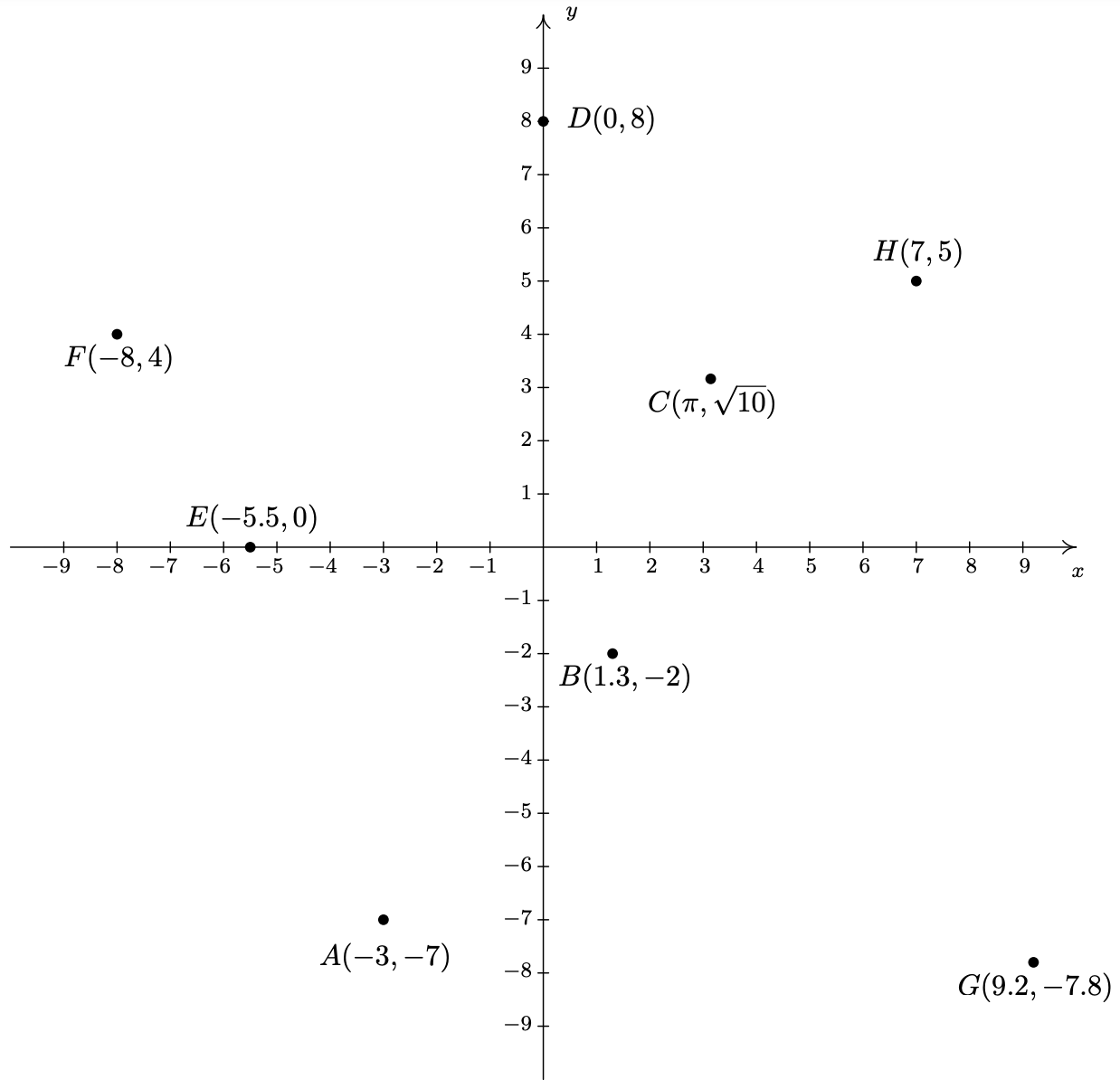
21. 1. El punto\(A(-3, -7)\) es
       • en Quadrant III
       • simétrico alrededor\(x\) del eje con\((-3, 7)\)
       • simétrico alrededor\(y\) del eje con\((3, -7)\)
       • simétrico sobre el origen con\((3, 7)\)
    2. El punto\(B(1.3, -2)\) es
       • en Cuadrante IV
       • simétrico alrededor\(x\) del eje con\((1.3, 2)\)
       • simétrico alrededor\(y\) del eje con\((-1.3, -2)\)
       • simétrico sobre el origen con\((-1.3, 2)\)
    3. El punto\(C(\pi, \sqrt{10})\) es
       • en Cuadrante I
       • simétrico alrededor\(x\) del eje con\((\pi, -\sqrt{10})\)
       • simétrico alrededor\(y\) del eje con\((-\pi, \sqrt{10})\)
       • simétrico sobre el origen con\((-\pi, -\sqrt{10})\)
    4. El punto\(D(0, 8)\) es
       • en el\(y\) eje positivo
       • simétrico alrededor\(x\) del eje con\((0, -8)\)
       • simétrico alrededor\(y\) del eje con\((0, 8)\)
       • simétrico sobre el origen con\((0, -8)\)
    5. El punto\(E(-5.5, 0)\) es
       • en el\(x\) eje negativo
       • simétrico alrededor\(x\) del eje con\((-5.5, 0)\)
       • simétrico alrededor\(y\) del eje con\((5.5, 0)\)
       • simétrico sobre el origen con\((5.5, 0)\)
    6. El punto\(F(-8, 4)\) es
       • en Quadrant II
       • simétrico alrededor\(x\) del eje con\((-8, -4)\)
       • simétrico alrededor\(y\) del eje con\((8, 4)\)
       • simétrico sobre el origen con\((8, -4)\)
    7. El punto\(G(9.2, -7.8)\) es
       • en Cuadrante IV
       • simétrico alrededor\(x\) del eje con\((9.2, 7.8)\)
       • simétrico alrededor\(y\) del eje con\((-9.2, -7.8)\)
       • simétrico sobre el origen con\((-9.2, 7.8)\)
    8. El punto\(H(7, 5)\) es
       • en Cuadrante I
       • simétrico alrededor\(x\) del eje con\((7, -5)\)
       • simétrico alrededor\(y\) del eje con\((-7, 5)\)
       • simétrico sobre el origen con\((-7, -5)\)
22. \(d = 5\),\(M = \left(-1, \frac{7}{2} \right)\)
23. \(d = 4 \sqrt{10}\),\(M = \left(1, -4 \right)\)
24. \(d = \sqrt{26}\),\(M = \left(1, \frac{3}{2} \right)\)
25. \(d= \frac{\sqrt{37}}{2}\),\(M = \left(\frac{5}{6}, \frac{7}{4} \right)\)
26. \(d = \sqrt{74}\),\(M = \left(\frac{13}{10}, -\frac{13}{10} \right)\)
27. \(d= 3\sqrt{5}\),\(M = \left(-\frac{\sqrt{2}}{2}, -\frac{\sqrt{3}}{2} \right)\)
28. \(d = \sqrt{83}\),\(M = \left(4 \sqrt{5}, \frac{5 \sqrt{3}}{2} \right)\)
29. \(d = \sqrt{x^2 + y^2}\),\(M = \left( \frac{x}{2}, \frac{y}{2}\right)\)
30. \((3 + \sqrt{7}, -1)\),\((3-\sqrt{7}, -1)\)
31. \((0,3)\)
32. \((-1+\sqrt{3},0)\),\((-1-\sqrt{3},0)\)
33. \(\left(\frac{\sqrt{2}}{2},-\frac{\sqrt{2}}{2} \right)\),\(\left(-\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2}\right)\)
34. \((-3, -4)\),\(5\) millas,\((4, -4)\)

37. 1. La distancia de\(A\) a\(B\) es\(|AB| = \sqrt{13}\), la distancia de\(A\) a\(C\) es\(|AC| = \sqrt{52}\), y la distancia de\(B\) a\(C\) es\(|BC| = \sqrt{65}\). Ya que\(\left(\sqrt{13}\right)^2 + \left( \sqrt{52} \right)^2 = \left( \sqrt{65} \right)^2\), estamos garantizados por el que el triángulo es un triángulo rectángulo.
    2. Demostrar que\(|AC|^{2} + |BC|^{2} = |AB|^{2}\)

---

Referencia

^1.. para ser leído como 'buena, sólida retroalimentación de colegas'..

² Para un ejemplo más estimulante, considera la colección de todas las cosas que no se contienen, esto lleva a la famosa Paradoja de Russell.

³ División larga, ¿alguien?

⁴ Se anima al lector a investigar Diagramas de Venn para una interpretación geométrica agradable de estos conceptos.

⁵ Así llamado en honor a René Descartes.

⁶ Las etiquetas pueden variar dependiendo del contexto de aplicación.

⁷ Por lo general, extendiéndose hacia el infinito se indica con flechas, pero aquí, las flechas se utilizan para indicar la dirección de los valores crecientes de\(\ x\) y\(\ y\).

⁸ Nuevamente, los nombres de las coordenadas pueden variar dependiendo del contexto de la aplicación. Si, por ejemplo, el eje horizontal representaba el tiempo podríamos optar por llamarlo el eje t. El primer número en el par ordenado sería entonces la coordenada t.

⁹ También llamadas las 'coordenadas rectangulares' de P — ver Sección 11.4 para más detalles.

¹⁰ La letra casi siempre\(\ O\) está reservada para el origen.

¹¹ Según Carl. Jeff piensa que la simetría está sobrevalorada.

¹² Hay quienes no están de acuerdo con esta afirmación. Búscalos en Internet alguna vez cuando estés aburrido.