1.2: Relaciones
- Page ID
- 119442
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Desde un punto de vista, 1 todo el Precálculo puede pensarse como estudiar conjuntos de puntos en el plano. Con el Plano Cartesiano ahora fresco en nuestra memoria podemos discutir esos conjuntos con más detalle y como es habitual, comenzamos con una definición.
Una relación es un conjunto de puntos en el plano.
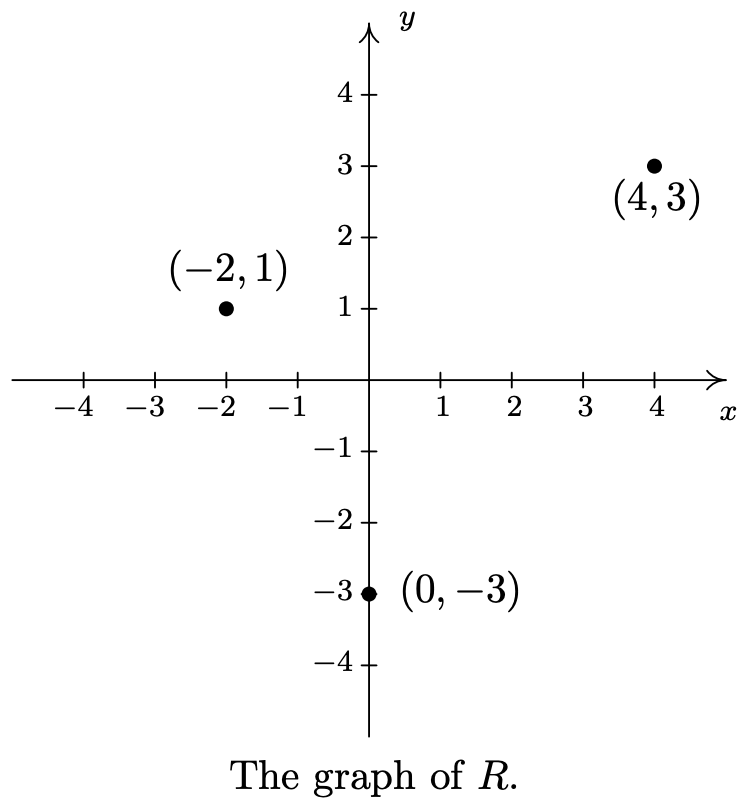
Dado que las relaciones son conjuntos, podemos describirlas utilizando las técnicas presentadas en la Sección 1.1.1. Es decir, podemos describir una relación verbalmente, usando el método roster, o usando notación set-builder. Dado que los elementos en una relación son puntos en el plano, a menudo tratamos de describir la relación gráfica o algebraicamente también. Dependiendo de la situación, un método puede ser más fácil o más cómodo de usar que otro. Como ejemplo, considere la relación\(\ R=\{(-2,1),(4,3),(0,-3)\}\). Como está escrito,\(\ R\) se describe usando el método de roster. Ya que\(\ R\) consiste en puntos en el plano, seguimos nuestro instinto y trazamos los puntos. Hacerlo produce la gráfica de\(\ R\).
En el siguiente ejemplo, graficamos una variedad de relaciones.
Grafica las siguientes relaciones.
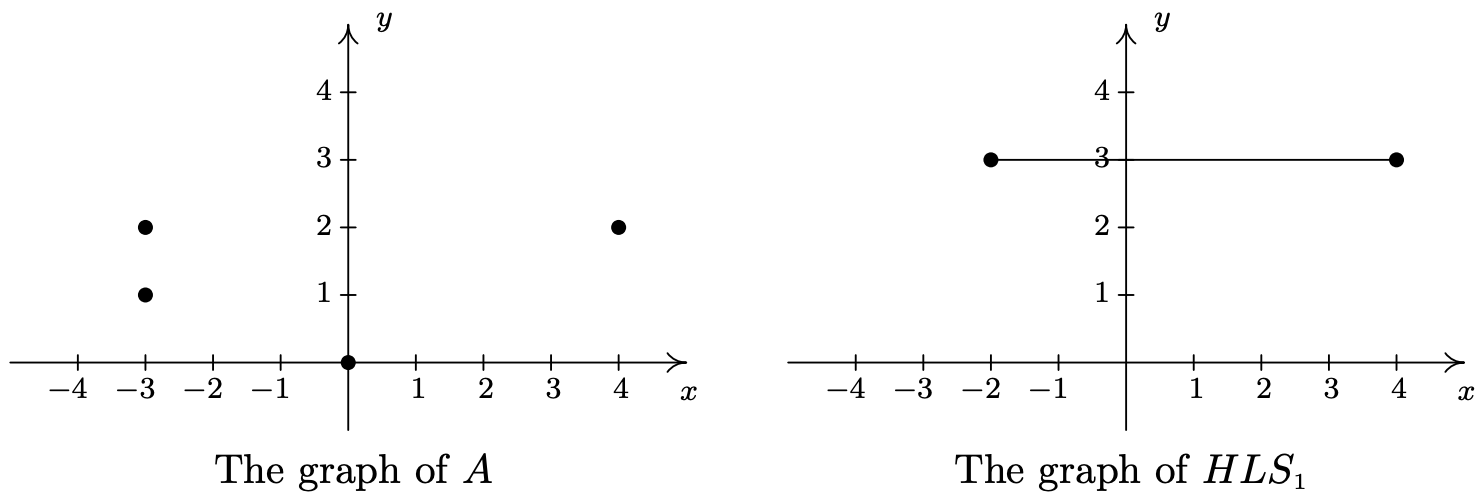
- \(\ A=\{(0,0),(-3,1),(4,2),(-3,2)\}\)
- \(\ H L S_{1}=\{(x, 3) \mid-2 \leq x \leq 4\}\)
- \(\ H L S_{2}=\{(x, 3) \mid-2 \leq x<4\}\)
- \(\ V=\{(3, y) \mid y \text { is a real number }\}\)
- \(\ H=\{(x, y) \mid y=-2\}\)
- \(\ R=\{(x, y) \mid 1<y \leq 3\}\)
Solución
- Para graficar\(\ A\), simplemente trazamos todos los puntos a los que pertenecen\(\ A\), como se muestra a continuación a la izquierda.
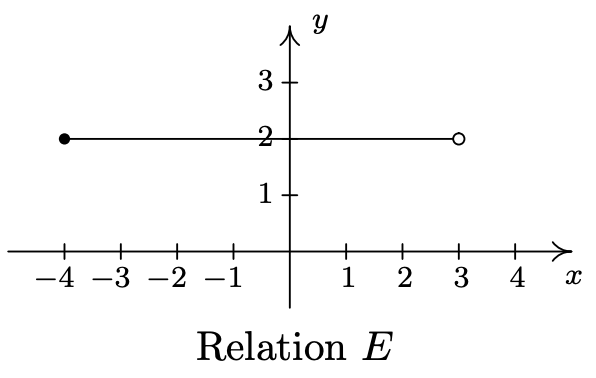
- No dejes que la notación en esta parte te engañe. El nombre de esta relación es\(\ H L S_{1}\), al igual que lo fue el nombre de la relación en el número 1\(\ A\). Las letras y los números son solo parte de su nombre, al igual que los números y letras de la frase 'Rey Jorge III' formaban parte del nombre de George. En palabras,\(\ \{(x, 3) \mid-2 \leq x \leq 4\}\) lee 'el conjunto de puntos\(\ (x, 3)\) tales que'\(\ -2 \leq x \leq 4\). Todos estos puntos tienen la misma coordenada y, 3, pero se permite que la coordenada x varíe entre −2 y 4, inclusive. Algunos de los puntos que pertenecen\(\ H L S_{1}\) incluyen algunos puntos amistosos como: (−2, 3), (−1, 3), (0, 3), (1, 3), (2, 3), (3, 3) y (4, 3). No obstante,\(\ H L S_{1}\) también contiene los puntos\(\ (0.829,3),\left(-\frac{5}{6}, 3\right),(\sqrt{\pi}, 3)\), y así sucesivamente. Es imposible 2 enumerar todos estos puntos por lo que\(\ x\) se utiliza la variable. Trazar varios puntos representativos amistosos debería convencerte de que\(\ H L S_{1}\) describe el segmento de línea horizontal desde el punto (−2, 3) hasta e incluyendo el punto (4, 3).
- \(\ H L S_{2}\)es obsesionantemente similar a\(\ H L S_{1}\). De hecho, la única diferencia entre los dos es que en lugar de\(\ \text{‘}-2 \leq x \leq 4^\text{’}\) nosotros tenemos\(\ \text {‘}-2 \leq x<4 \text {'}\). Esto significa que todavía obtenemos un segmento de línea horizontal que incluye (−2, 3) y se extiende a (4, 3), pero no incluimos (4, 3) debido a la estricta desigualdad x < 4. ¿Cómo denotamos esto en nuestra gráfica? Es un error común hacer que la gráfica comience en (−2, 3) y termine en (3, 3) como se muestra a continuación a la izquierda. El problema con esta gráfica es que nos estamos olvidando de los puntos como (3.1, 3), (3.5, 3), (3.9, 3), (3.99, 3), y así sucesivamente. No hay un número real que venga 'inmediatamente antes' 4, así que para describir el conjunto de puntos que queremos, dibujamos el segmento de línea horizontal comenzando en (−2, 3) y dibujamos un círculo abierto en (4, 3) como se representa a continuación a la derecha.

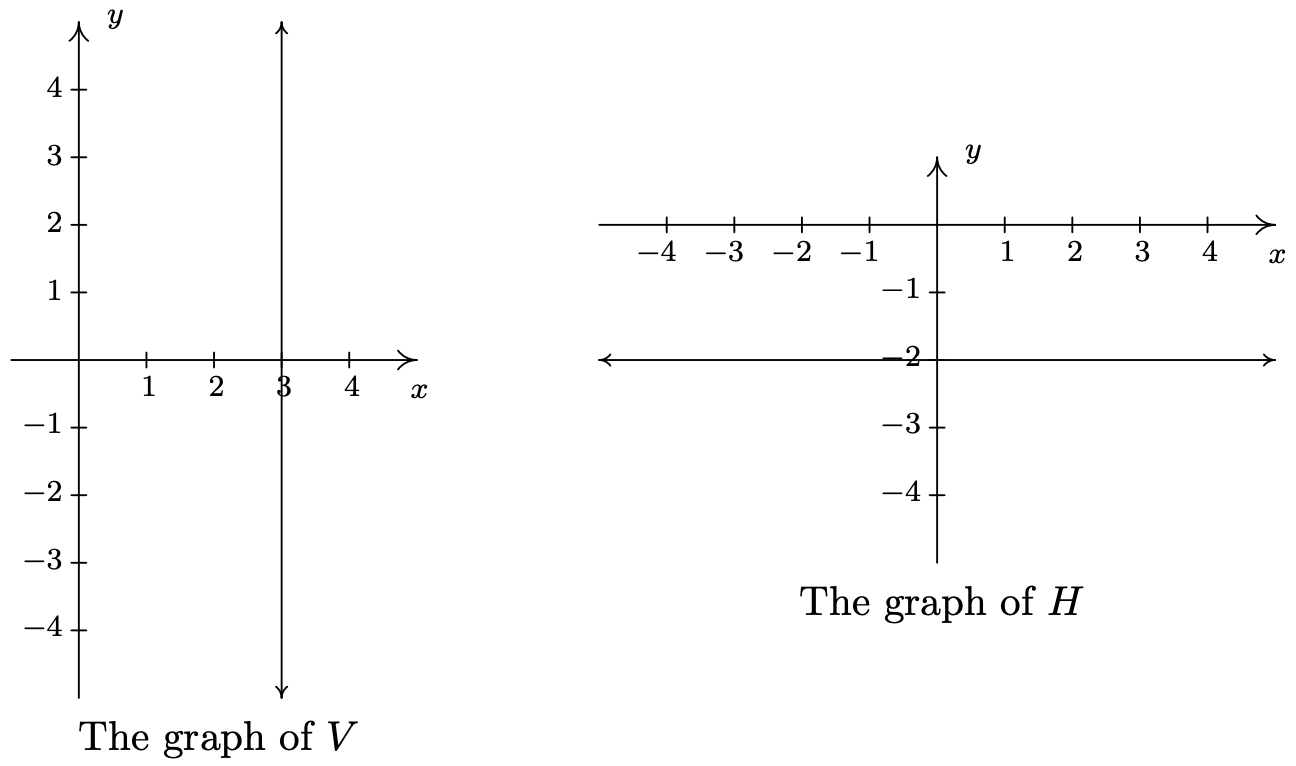
- A continuación, llegamos a la relación\(\ V\), descrita como el conjunto de puntos\(\ (3, y)\) tal que\(\ y\) es un número real. Todos estos puntos tienen una coordenada x de 3, pero la coordenada y es libre de ser lo que quiera ser, sin restricción. 3 Trazar algunos puntos 'amistosos' de\(\ V\) debería convencerte de que todos los puntos de\(\ V\) mentira en la línea vertical 4\(\ x = 3\). Como no hay restricción en la coordenada y, colocamos flechas al final de la porción de la línea que dibujamos para indicar que se extiende indefinidamente en ambas direcciones. La gráfica de\(\ V\) está abajo a la izquierda.
- Aunque escrita de manera ligeramente diferente, la relación\(\ H=\{(x, y) \mid y=-2\}\) es similar a la relación\(\ V\) anterior en que solo se especifica una de las coordenadas, en este caso la coordenada y, dejando\(\ x\) que sea 'libre'. Trazar algunos puntos representativos nos da la línea horizontal\(\ y = −2\).
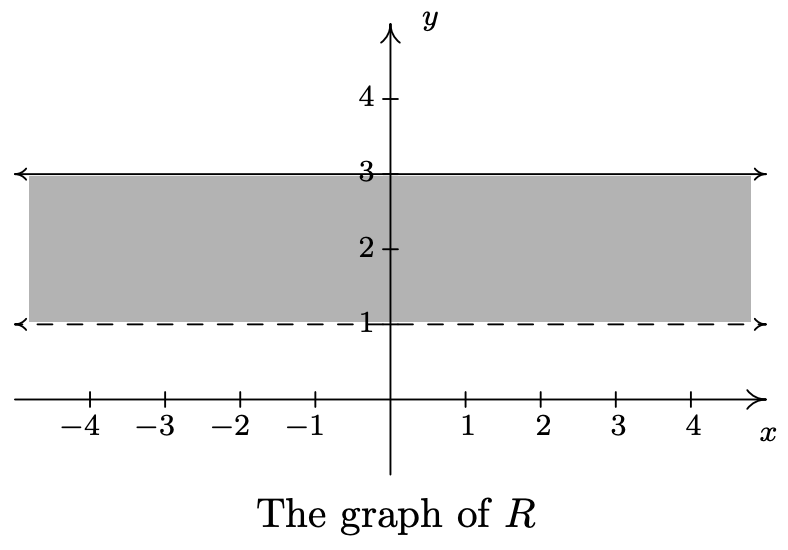
- Para nuestro último ejemplo, recurrimos a\(\ R=\{(x, y) \mid 1<y \leq 3\}\). Al igual que en el ejemplo anterior,\(\ x\) es libre de ser lo que quiera. El valor de\(\ y\), en cambio, si bien no es completamente libre, está permitido deambular entre 1 y 3 excluyendo 1, pero incluyendo 3. Después de trazar unos 5 elementos amigables de\(\ R\), debería quedar claro que\(\ R\) consiste en la región entre las líneas horizontales\(\ y = 1\) y\(\ y = 3\). Dado que\(\ R\) requiere que las coordenadas y sean mayores que 1, pero no iguales a 1, trazamos la línea\(\ y = 1\) para indicar que esos puntos no pertenecen a\(\ R\).
Las relaciones\(\ V\) y\(\ H\) en el ejemplo anterior nos llevan a nuestra forma final de describir las relaciones: algebraicamente. Podemos describir más sucintamente los puntos en\(\ V\) como aquellos puntos que satisfacen la ecuación '\(\ x = 3\)'. Lo más probable es que hayas visto ecuaciones como esta antes. Dependiendo del contexto, '\(\ x = 3\)' podría significar que hemos resuelto una ecuación\(\ x\) y hemos llegado a la solución\(\ x = 3\). En este caso, sin embargo, '\(\ x = 3\)' describe un conjunto de puntos en el plano cuya coordenada x es 3. De igual manera, la relación\(\ H\) anterior puede ser descrita por la ecuación '\(\ y = −2\)'. En algún momento de tu educación matemática, probablemente aprendiste lo siguiente.
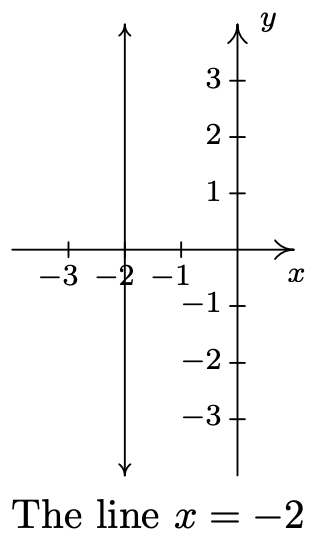
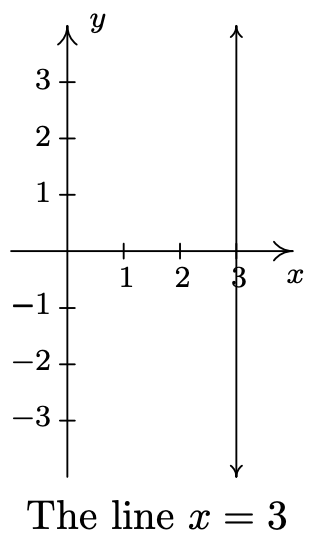
- La gráfica de la ecuación\(\ x = a\) es una línea vertical pasante\(\ (a, 0)\).
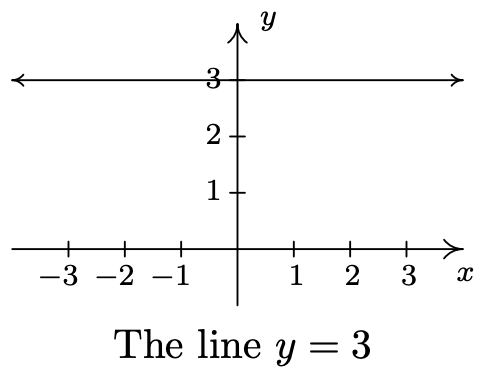
- La gráfica de la ecuación\(\ y = b\) es una línea horizontal a través\(\ (0, b)\).
Dado que las ecuaciones muy simples\(\ x = a\) y las líneas\(\ y = b\) producidas, es natural preguntarse qué formas podrían dar otras ecuaciones. Así, nuestro siguiente objetivo es estudiar las gráficas de ecuaciones en un entorno más general a medida que continuamos uniendo Álgebra y Geometría.
1.2.1 Gráficas de Ecuaciones
En esta sección, profundizamos en la conexión entre Álgebra y Geometría enfocándonos en graficar las relaciones descritas por ecuaciones. La idea principal de esta sección es la siguiente.
La gráfica de una ecuación es el conjunto de puntos que satisfacen la ecuación. Es decir, un punto\(\ (x, y)\) está en la gráfica de una ecuación si y sólo si\(\ x\) y\(\ y\) satisfacer la ecuación.
Aquí, '\(\ x\)y\(\ y\) satisfacer la ecuación' significa'\(\ x\) y\(\ y\) hacer realidad la ecuación'. Es en este punto que obtenemos alguna idea de la palabra 'relación'. Si la ecuación a graficar contiene ambas\(\ x\) y\(\ y\), entonces la ecuación misma es la que está relacionando las dos variables. Más específicamente, en los siguientes dos ejemplos, consideramos la gráfica de la ecuación\(\ x^{2}+y^{3}=1\). A pesar de que no está específicamente deletreada, lo que estamos haciendo es graficar la relación\(\ R=\left\{(x, y) \mid x^{2}+y^{3}=1\right\}\). Los puntos\(\ (x, y)\) que graficamos pertenecen a la relación\(\ R\) y están necesariamente relacionados por la ecuación\(\ x^{2}+y^{3}=1\), ya que son esos pares de\(\ x\) y los\(\ y\) que hacen que la ecuación sea verdadera.
Determinar si\(\ (2, −1)\) está o no en la gráfica de\(\ x^{2}+y^{3}=1\).
Solución
Sustituimos\(\ x = 2\) y\(\ y = −1\) en la ecuación para ver si la ecuación está satisfecha.
\ (\\ begin {alineado}
(2) ^ {2} + (-1) ^ {3}\ stackrel {?} {=} &1\\
3\ neq &1
\ end {alineado}\)
De ahí, no\(\ (2, −1)\) está en la gráfica de\(\ x^{2}+y^{3}=1\).
Podríamos pasar horas adivinando y comprobando al azar para ver si los puntos están en la gráfica de la ecuación. En el siguiente ejemplo se esboza un enfoque más sistemático.
Gráfica\(\ x^{2}+y^{3}=1\).
Solución
Para generar eficientemente puntos en la gráfica de esta ecuación, primero resolvemos para\(\ y\)
\ (\\ begin {alineado}
x^ {2} +y^ {3} &=1\\
y^ {3} &=1-x^ {2}\
\ sqrt [3] {y^ {3}} &=\ sqrt [3] {1-x^ {2}}\\
y &=\ sqrt [3] {1-x^ {2}}
\ end {alineado}\)
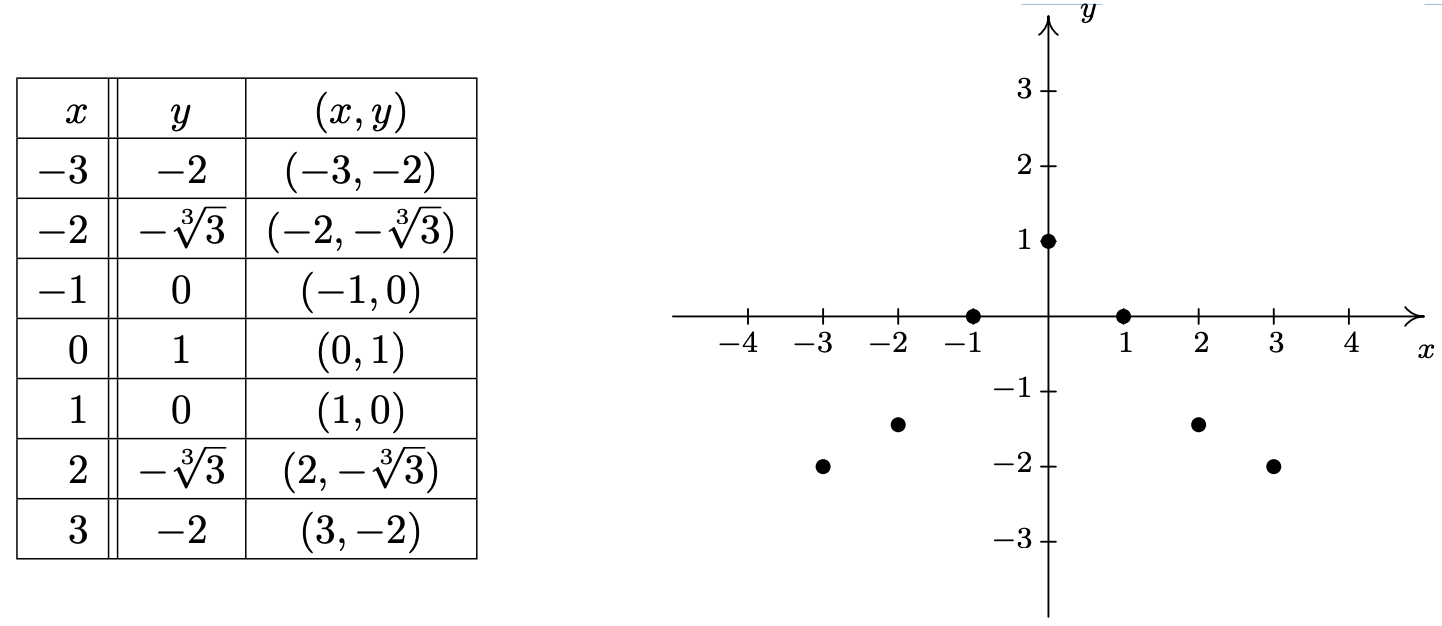
Ahora sustituimos un valor en for\(\ x\), determinamos el valor\(\ y\) correspondiente y trazamos el punto resultante\(\ (x, y)\). Por ejemplo, sustituir\(\ x = −3\) en la ecuación rinde
\(\ y=\sqrt[3]{1-x^{2}}=\sqrt[3]{1-(-3)^{2}}=\sqrt[3]{-8}=-2,\)
así que el punto\(\ (−3, −2)\) está en la gráfica. Continuando de esta manera, generamos una tabla de puntos que están en la gráfica de la ecuación. Estos puntos se trazan luego en el plano como se muestra a continuación.
Recuerde, estos puntos constituyen sólo un pequeño muestreo de los puntos en la gráfica de esta ecuación. Para tener una mejor idea de la forma de la gráfica, podríamos trazar más puntos hasta que nos sintamos cómodos 'conectando los puntos'. Hacerlo resultaría en una curva similar a la que se muestra a continuación en el extremo izquierdo.
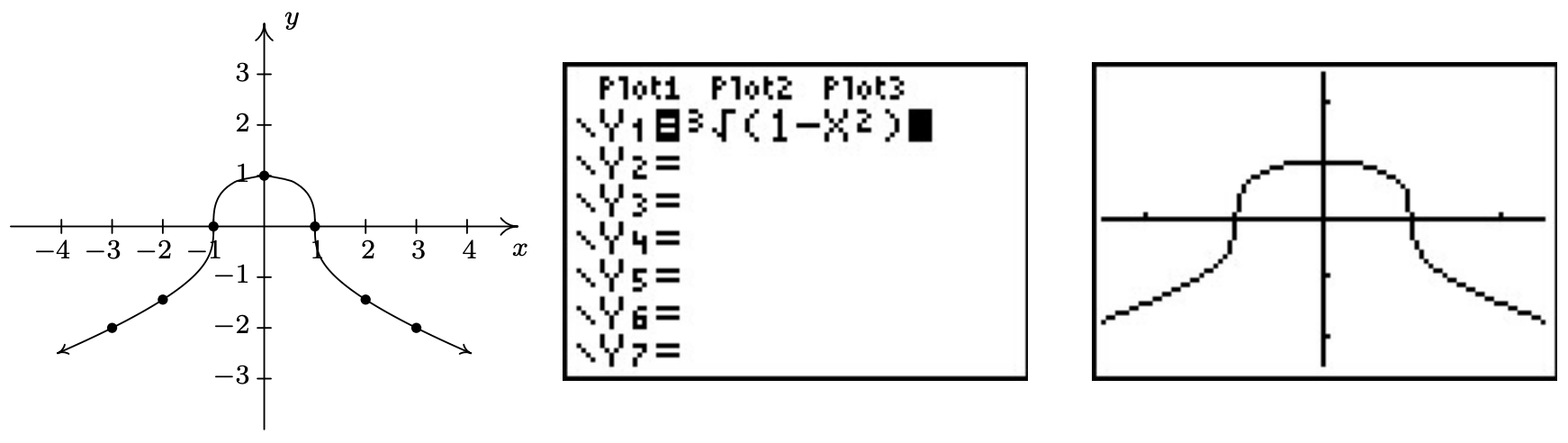
No se preocupe si no obtiene todas las pequeñas curvas y curvas a la derecha − Cálculo es donde el arte de la gráfica precisa toma protagonismo. Por ahora, nos conformaremos con nuestro ingenuo enfoque de 'plug and plot' para graficar. Si sientes que todo este tedioso cálculo y trazado está debajo de ti, entonces puedes buscar una calculadora gráfica, ingresar la fórmula como se muestra arriba y graficar.
De todos los puntos en la gráfica de una ecuación, los lugares donde la gráfica cruza o toca los ejes tienen un significado especial. A estos se les llama las intercepciones de la gráfica. Los interceptos vienen en dos variedades distintas: intercepciones x e intercepciones y. Se definen a continuación.
Supongamos que se da la gráfica de una ecuación.
- Un punto en una gráfica que también está en el eje x se denomina intercepción x de la gráfica.
- Un punto en una gráfica que también está en el eje y se llama una intercepción y de la gráfica.
En nuestro ejemplo anterior la gráfica tenía dos intercepciones x, (−1, 0) y (1, 0), y una intercepción y, (0, 1). La gráfica de una ecuación puede tener cualquier número de intercepciones, ¡incluyendo ninguna en absoluto! Dado que las intercepciones x se encuentran en el eje x, podemos encontrarlas estableciendo y = 0 en la ecuación. De manera similar, dado que las intercepciones y se encuentran en el eje y, podemos encontrarlas estableciendo x = 0 en la ecuación. Tenga en cuenta que las intercepciones son puntos y por lo tanto deben escribirse como pares ordenados. Para resumir,
Dada una ecuación que involucra x e y, encontramos las intercepciones de la gráfica de la siguiente manera:
- x-intercepts tienen la forma (x, 0); establecer y = 0 en la ecuación y resolver para x.
- las intercepciones y tienen la forma (0, y); establecer x = 0 en la ecuación y resolver para y.
Otro dato que quizás hayas notado sobre la gráfica en el ejemplo anterior es que parece ser simétrica alrededor del eje y. Para probar esto analíticamente, asumimos que (x, y) es un punto genérico en la gráfica de la ecuación. Es decir, suponemos que\(\ x^{2}+y^{3}=1\) es verdad. Como aprendimos en la Sección 1.1, el punto simétrico a (x, y) alrededor del eje y es (−x, y). Para mostrar que la gráfica es simétrica alrededor del eje y, necesitamos mostrar que (−x, y) satisface la ecuación\(\ x^{2}+y^{3}=1\), también. Sustituir (−x, y) en la ecuación da
\ (\\ begin {array} {rll}
(-x) ^ {2} + (y) ^ {3} &\ stackrel {?} {=} & 1\\
x^ {2} +y^ {3} &\ stackrel {\ checkmark} {=} & 1
\ end {array}\)
Como estamos asumiendo que la ecuación original\(\ x^{2}+y^{3}=1\) es verdadera, hemos demostrado que (−x, y) satisface la ecuación (ya que conduce a un resultado verdadero) y por lo tanto está en la gráfica. De esta manera, podemos comprobar si la gráfica de una ecuación dada posee alguna de las simetrías discutidas en la Sección 1.1. Resumimos el procedimiento en el siguiente resultado.
Para probar la simetría de la gráfica de una ecuación
- sobre el eje y − sustituya (−x, y) en la ecuación y simplifique. Si el resultado es equivalente a la ecuación original, la gráfica es simétrica alrededor del eje y.
- sobre el eje x — sustituir (x, −y) en la ecuación y simplificar. Si el resultado es equivalente a la ecuación original, la gráfica es simétrica alrededor del eje x.
- sobre el origen - sustituir (−x, −y) en la ecuación y simplificar. Si el resultado es equivalente a la ecuación original, la gráfica es simétrica sobre el origen.
Las intercepciones y la simetría son dos herramientas que pueden ayudarnos a esbozar la gráfica de una ecuación analíticamente, como se demuestra en el siguiente ejemplo.
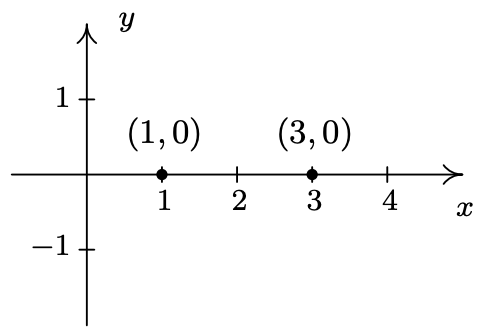
Encuentra las intercepciones x e y (si las hay) de la gráfica de\(\ (x-2)^{2}+y^{2}=1\). Prueba de simetría. Trace puntos adicionales según sea necesario para completar la gráfica.
Solución
Para buscar intercepciones x, establecemos y = 0 y resolvemos
\ (\\ begin {alineado}
(x-2) ^ {2} +y^ {2} &=1\\
(x-2) ^ {2} +0^ {2} &=1\\
(x-2) ^ {2} &=1\
\\ sqrt {(x-2) ^ {2}} &=\ sqrt {1}\ quad\ quad\ quad\ text {extraer raíces cuadradas}\
x-2 &=\ pm 1\\
x &=2\ pm 1\\
x &=3,1
\ final {alineado}\)
Obtenemos dos respuestas para x que corresponden a dos intercepciones x: (1, 0) y (3, 0). Volviendo nuestra atención a las intercepciones y, establecemos x = 0 y resolvemos
\ (\\ begin {alineado}
(x-2) ^ {2} +y^ {2} &=1\\
(0-2) ^ {2} +y^ {2} &=1\\
4+y^ {2} &=1\\
y^ {2} &=-3
\ end {alineado}\)
Ya que no hay un número real que cuadre a un número negativo (¿Recuerdas por qué?) , nos vemos obligados a concluir que la gráfica no tiene intercepciones y.
Trazar los datos que tenemos hasta ahora, obtenemos
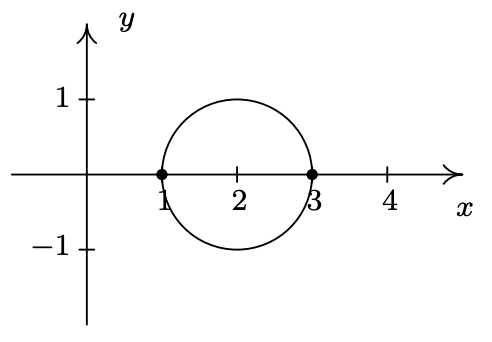
Avanzando hacia la simetría, podemos descartar inmediatamente la posibilidad de que la gráfica sea simétrica alrededor del eje y o del origen. Si la gráfica poseyera alguna de estas simetrías, entonces el hecho de que (1, 0) esté en la gráfica significaría que (−1, 0) tendría que estar en la gráfica. (¿Por qué?) Como (−1, 0) sería otra intercepción x (y hemos encontrado todas ellas), la gráfica no puede tener simetría de eje y ni origen. La única simetría que queda por probar es la simetría alrededor del eje x. Para ello, sustituimos (x, −y) en la ecuación y simplificamos
\ (\\ begin {alineado}
(x-2) ^ {2} +y^ {2} =&1\\
(x-2) ^ {2} + (-y) ^ {2}\ stackrel {?} {=} &1\\
(x-2) ^ {2} +y^ {2}\ stackrel {\ checkmark} {=} &1
\ end {alineado}\)
Desde que hemos obtenido nuestra ecuación original, sabemos que la gráfica es simétrica respecto al eje x. Esto significa que podemos cortar nuestro tiempo de 'tapar y trazar' a la mitad: lo que ocurra debajo del eje x se refleja por encima del eje x, y viceversa. Procediendo como hicimos en el ejemplo anterior, obtenemos
Un par de observaciones están en orden. En primer lugar, es totalmente posible elegir un valor para x que no corresponda a un punto de la gráfica. Por ejemplo, en el ejemplo anterior, si resolvemos por y como es nuestra costumbre, obtenemos
\(\ y=\pm \sqrt{1-(x-2)^{2}}\)
Al sustituir x = 0 en la ecuación, obtendríamos
\(\ y=\pm \sqrt{1-(0-2)^{2}}=\pm \sqrt{1-4}=\pm \sqrt{-3},\)
que no es un número real. Esto significa que no hay puntos en la gráfica con una coordenada x de 0. Cuando esto sucede, seguimos adelante e intentamos otro punto. Este es otro inconveniente del enfoque 'plug-and-plot' para graficar ecuaciones. Por suerte, dedicaremos gran parte del resto de este libro a desarrollar técnicas que nos permitan graficar familias enteras de ecuaciones rápidamente. 6 En segundo lugar, es instructivo mostrar lo que hubiera sucedido si hubiéramos probado la ecuación en el último ejemplo para la simetría alrededor del eje y. Sustituir (−x, y) en la ecuación rinde
\ (\\ begin {array} {rll}
(x-2) ^ {2} +y^ {2} & = & 1\\
(-x-2) ^ {2} +y^ {2} &\ stackrel {?} {=} & 1\\
((-1) (x+2)) ^ {2} +y^ {2} &\ stackrel {?} {=} & 1\\
(x+2) ^ {2} +y^ {2} &\ stackrel {?} {=} & 1.
\ end {array}\)
Esta última ecuación no parece ser equivalente a nuestra ecuación original. Sin embargo, para probar realmente que la gráfica no es simétrica alrededor del eje y, necesitamos encontrar un punto (x, y) en la gráfica cuya reflexión (−x, y) no lo es. Nuestra intercepción x (1, 0) se ajusta muy bien a este proyecto de ley, ya que si sustituimos (−1, 0) en la ecuación obtenemos
\ (\\ begin {alineado}
(x-2) ^ {2} +y^ {2} &\ stackrel {?} {=} 1\\
(-1-2) ^ {2} +0^ {2} &\ neq 1\\
9 &\ neq 1.
\ end {alineado}\)
Esto demuestra que (−1, 0) no está en la gráfica.
1.2.2 Ejercicios
En los Ejercicios 1 - 20, grafica la relación dada.
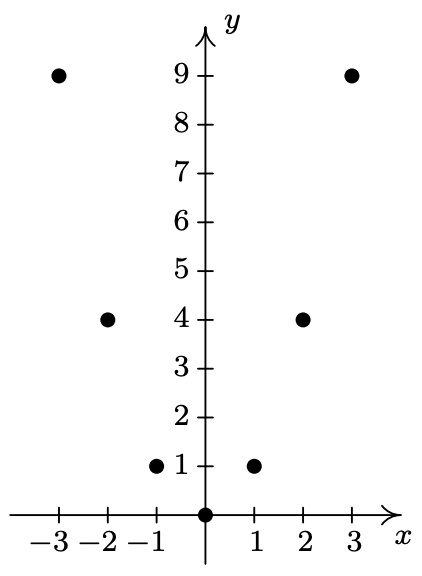
- \(\ \{(-3,9),(-2,4),(-1,1),(0,0),(1,1),(2,4),(3,9)\}\)
- \(\ \{(-2,0),(-1,1),(-1,-1),(0,2),(0,-2),(1,3),(1,-3)\}\)
- \(\ \{(m, 2 m) \mid m=0, \pm 1, \pm 2\}\)
- \(\ \left\{\left(\frac{6}{k}, k\right) \mid k=\pm 1, \pm 2, \pm 3, \pm 4, \pm 5, \pm 6\right\}\)
- \(\ \left\{\left(n, 4-n^{2}\right) \mid n=0, \pm 1, \pm 2\right\}\)
- \(\ \{(\sqrt{j}, j) \mid j=0,1,4,9\}\)
- \(\ \{(x,-2) \mid x>-4\}\)
- \(\ \{(x, 3) \mid x \leq 4\}\)
- \(\ \{(-1, y) \mid y>1\}\)
- \(\ \{(2, y) \mid y \leq 5\}\)
- \(\ \{(-2, y) \mid-3<y \leq 4\}\)
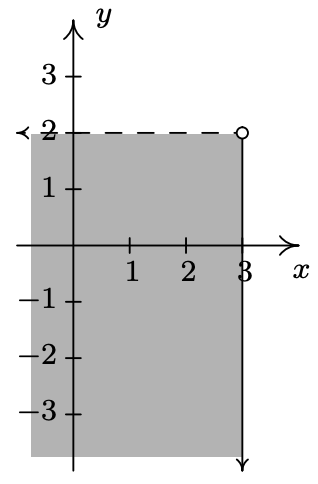
- \(\ \{(3, y) \mid-4 \leq y<3\}\)
- \(\ \{(x, 2) \mid-2 \leq x<3\}\)
- \(\ \{(x,-3) \mid-4<x \leq 4\}\)
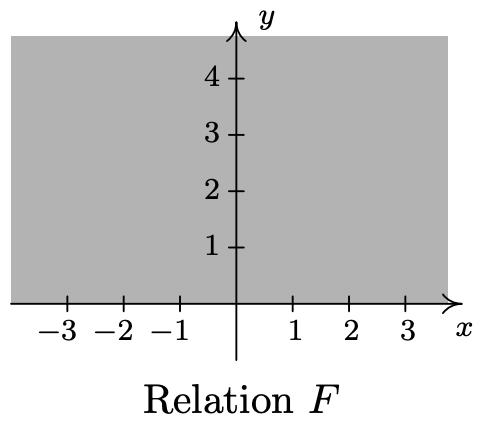
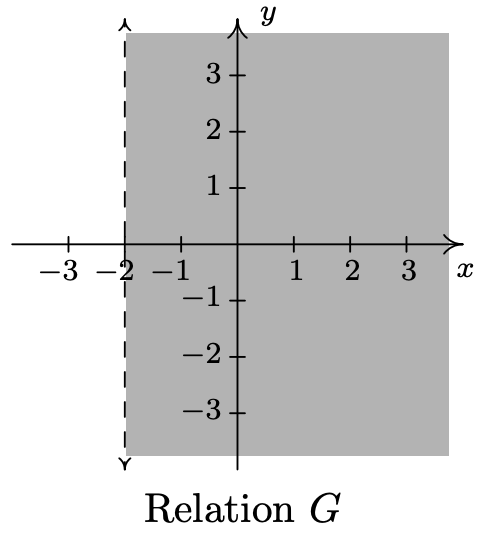
- \(\ \{(x, y) \mid x>-2\}\)
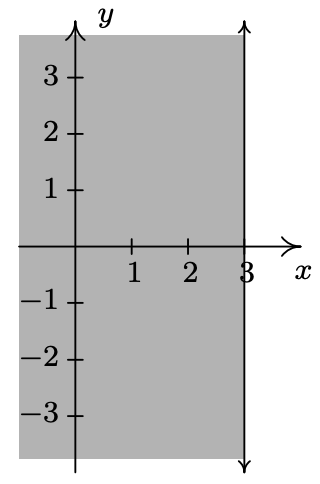
- \(\ \{(x, y) \mid x \leq 3\}\)
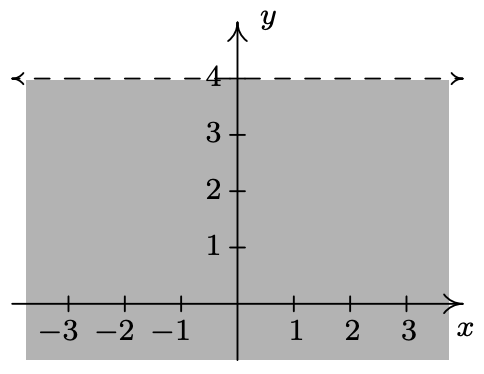
- \(\ \{(x, y) \mid y<4\}\)
- \(\ \{(x, y) \mid x \leq 3, y<2\}\)
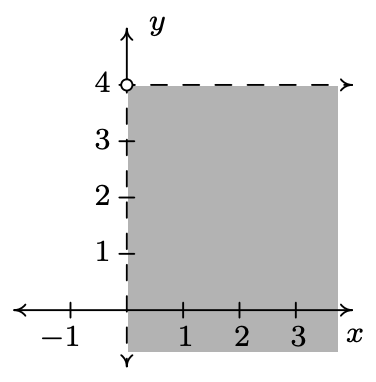
- \(\ \{(x, y) \mid x>0, y<4\}\)
- \(\ \left\{(x, y) \mid-\sqrt{2} \leq x \leq \frac{2}{3}, \pi<y \leq \frac{9}{2}\right\}\)
En los Ejercicios 21 - 30, describa la relación dada utilizando el método roster o set-builder.
En Ejercicios 31 - 36, grafica la línea dada.
- \(\ x = −2\)
- \(\ x = 3\)
- \(\ y = 3\)
- \(\ y = −2\)
- \(\ x = 0\)
- \(\ y = 0\)
Algunas relaciones son bastante fáciles de describir con palabras o con el método de roster pero son bastante difíciles, si no imposibles, de graficar. Discuta con tus compañeros de clase cómo podrías graficar las relaciones dadas en los Ejercicios 37 - 40. Tenga en cuenta que en la siguiente notación estamos usando los puntos suspensivos,.., para denotar que la lista no termina, sino que más bien, sigue siguiendo el patrón establecido indefinidamente. Para las relaciones en los Ejercicios 37 y 38, dar dos ejemplos de puntos que pertenecen a la relación y dos puntos que no pertenecen a la relación.
- \(\ \{(x, y) \mid x \text { is an odd integer, and } y \text { is an even integer. }\}\)
- \(\ \{(x, 1) \mid x \text { is an irrational number }\}\)
- \(\ \{(1,0),(2,1),(4,2),(8,3),(16,4),(32,5), \ldots\}\)
- \(\ \{\ldots,(-3,9),(-2,4),(-1,1),(0,0),(1,1),(2,4),(3,9), \ldots\}\)
Por cada ecuación dada en los Ejercicios 41 - 52:
- Encuentre la (s) intercepción (s) x e y de la gráfica, si existe alguna.
- Siga el procedimiento del Ejemplo 1.2.3 para crear una tabla de puntos de muestra en la gráfica de la ecuación.
- Trace los puntos de muestra y cree un boceto aproximado de la gráfica de la ecuación.
- Prueba de simetría. Si la ecuación parece fallar alguna de las pruebas de simetría, encuentre un punto en la gráfica de la ecuación cuya reflexión no pueda estar en la gráfica como se hizo al final del Ejemplo 1.2.4
- \(\ y=x^{2}+1\)
- \(\ y=x^{2}-2 x-8\)
- \(\ y=x^{3}-x\)
- \(\ y=\frac{x^{3}}{4}-3 x\)
- \(\ y=\sqrt{x-2}\)
- \(\ y=2 \sqrt{x+4}-2\)
- \(\ 3 x-y=7\)
- \(\ 3 x-2 y=10\)
- \(\ (x+2)^{2}+y^{2}=16\)
- \(\ x^{2}-y^{2}=1\)
- \(\ 4 y^{2}-9 x^{2}=36\)
- \(\ x^{3} y=-4\)
Los procedimientos que hemos esbozado en los Ejemplos de esta sección y utilizados en los Ejercicios 41 - 52 se basan en el hecho de que las ecuaciones fueron “bien portadas”. No todo en Matemáticas es tan manso, como te mostrarán las siguientes ecuaciones. Discuta con sus compañeros de clase cómo podría acercarse graficando las ecuaciones dadas en los Ejercicios 53 - 56. ¿Qué dificultades surgen al intentar aplicar las diversas pruebas y procedimientos que se dan en esta sección? Para obtener más información, incluyendo imágenes de las curvas, cada nombre de curva es un enlace a su página en www.Wikipedia.org. Para una lista mucho más larga de curvas fascinantes, haga clic aquí.
- \(\ x^{3}+y^{3}-3 x y=0\)Folio de Descartes
- \(\ x^{4}=x^{2}+y^{2}\)Kampyle de Eudoxus
- \(\ y^{2}=x^{3}+3 x^{2}\)Tschirnhausen cúbico
- \(\ \left(x^{2}+y^{2}\right)^{2}=x^{3}+y^{3}\)Huevo torcido
- Con la ayuda de tus compañeros, encuentra ejemplos de ecuaciones cuyas gráficas poseen
- simetría sobre el eje x solamente
- simetría sobre el eje y solamente
- simetría sobre el origen solamente
- simetría sobre el eje x, el eje y y el origen
¿Puedes encontrar un ejemplo de una ecuación cuya gráfica posea exactamente dos de las simetrías enumeradas anteriormente? ¿Por qué o por qué no?
1.2.3 Respuestas
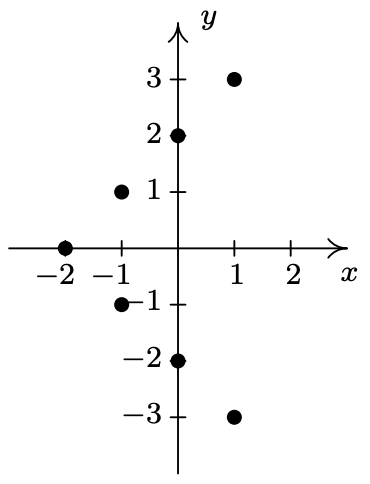
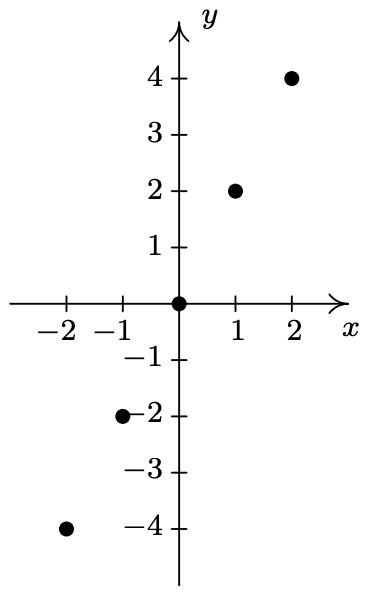
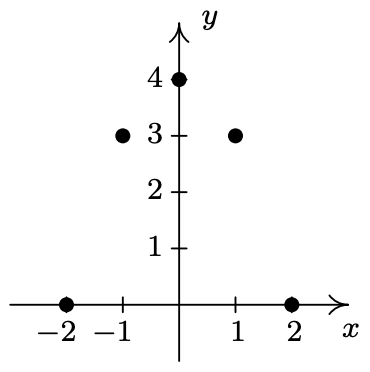
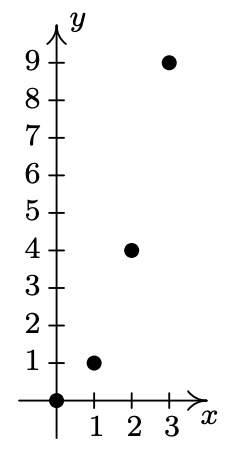
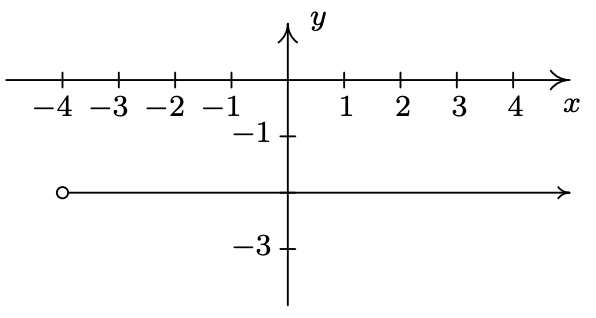
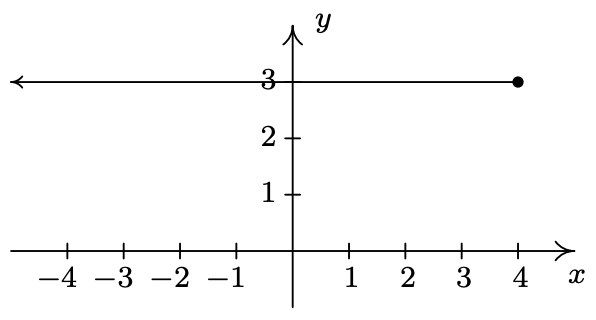

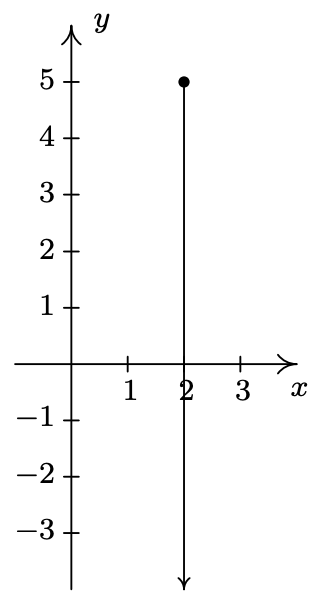
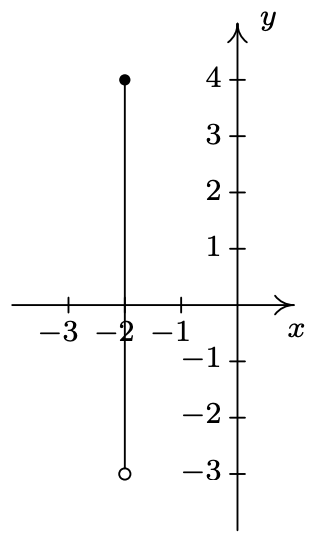
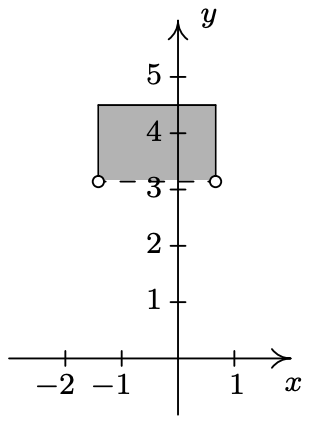
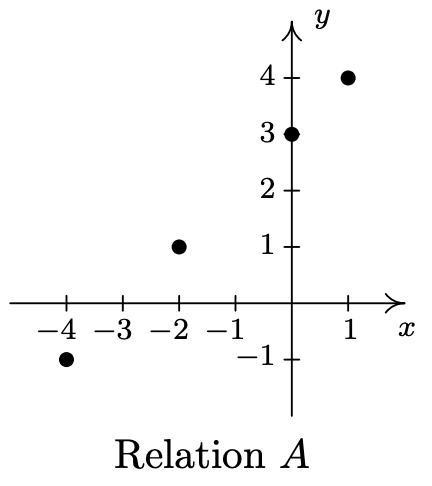
- \(\ A=\{(-4,-1),(-2,1),(0,3),(1,4)\}\)
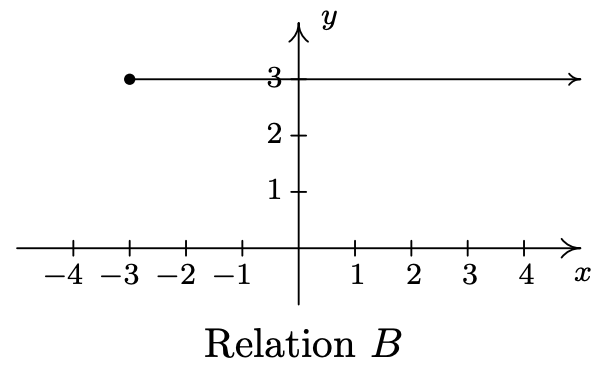
- \(\ B=\{(x, 3) \mid x \geq-3\}\)
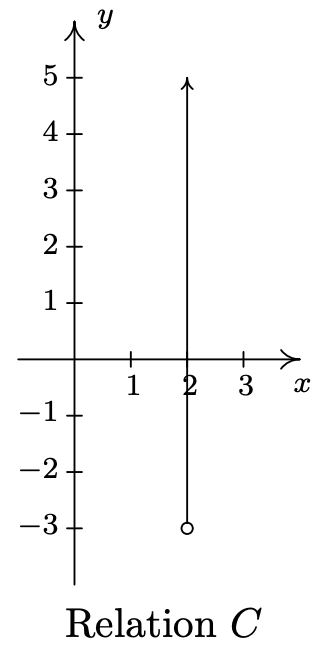
- \(\ C=\{(2, y) \mid y>-3\}\)
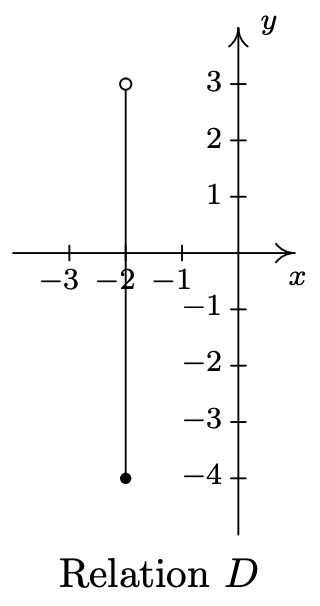
- \(\ D=\{(-2, y) \mid-4 \leq y<3\}\)
- \(\ E=\{(x, 2) \mid-4 \leq x<3\}\)
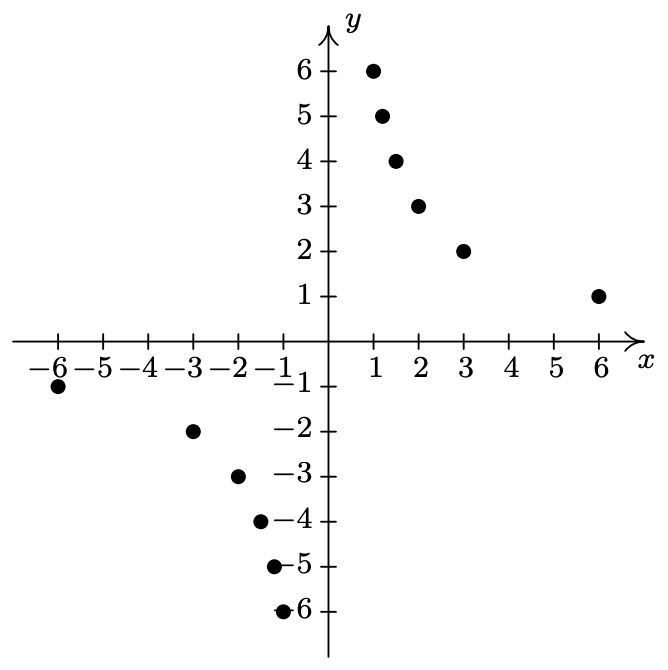
- \(\ F=\{(x, y) \mid y \geq 0\}\)
- \(\ G=\{(x, y) \mid x>-2\}\)
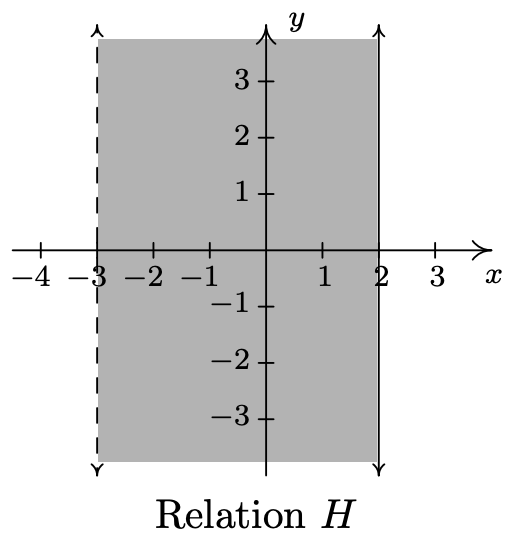
- \(\ H=\{(x, y) \mid-3<x \leq 2\}\)
- \(\ I=\{(x, y) \mid x \geq 0, y \geq 0\}\)
- \(\ J=\{(x, y) \mid-4<x<5,-3<y<2\}\)
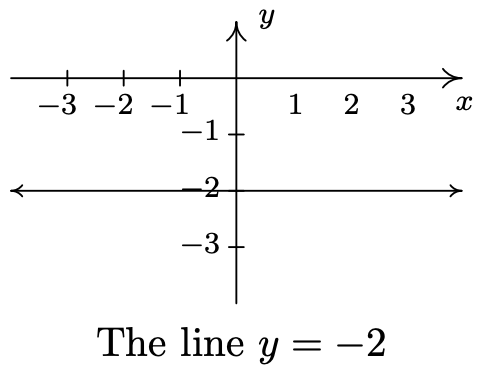
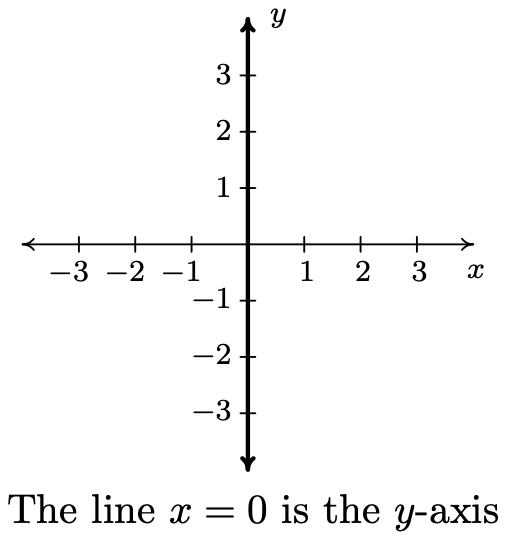
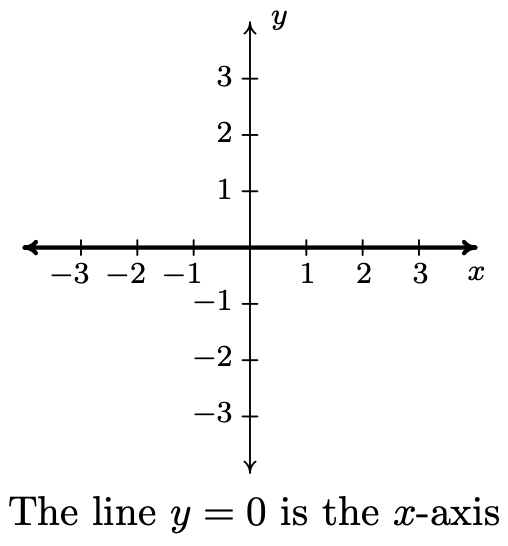
- \(\ y=x^{2}+1\)
La gráfica no tiene intercepciones x
intercepción en Y: (0, 1)
\(\ x\) \(\ y\) \(\ (x, y)\) −2 5 (−2, 5) −1 2 (−1, 2) 0 1 (0, 1) 1 2 (1, 2) 2 5 (2, 5) 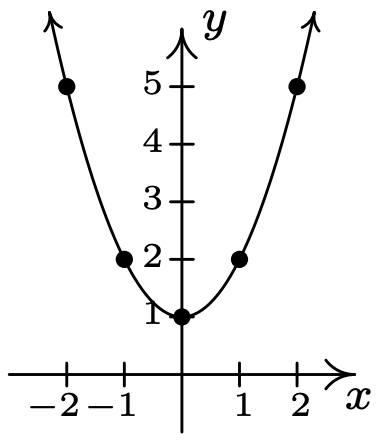
La gráfica no es simétrica con respecto al eje x (por ejemplo, (2, 5) está en la gráfica pero (2, −5) no lo es)
La gráfica es simétrica alrededor del eje y
La gráfica no es simétrica sobre el origen (por ejemplo, (2, 5) está en la gráfica pero (−2, −5) no lo es)
- \(\ y=x^{2}-2 x-8\)
intercepciones x: (4, 0), (−2, 0)
intersección en Y: (0, −8)
\(\ x\) \(\ y\) \(\ (x, y)\) −3 7 (−3, 7) −2 0 (−2, 0) −1 −5 (−1, −5) 0 −8 (0, −8) 1 −9 (1, −9) 2 −8 (2, −8) 3 −5 (3, −5) 4 0 (4, 0) 5 7 (5, 7) 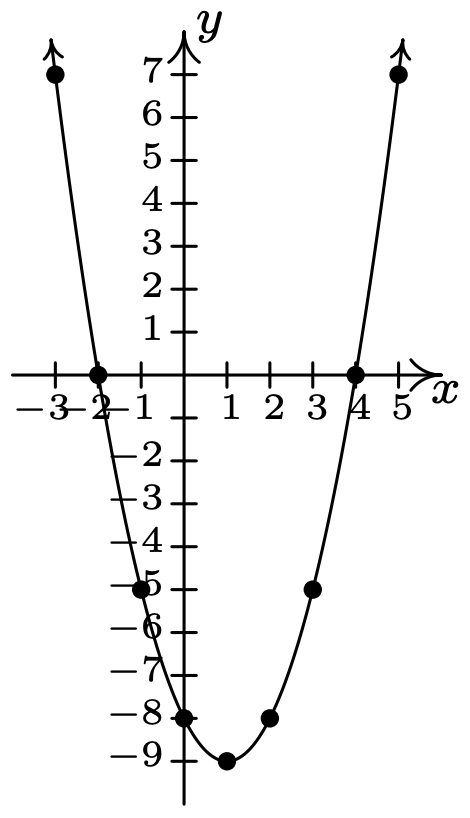
El gráfico no es simétrico con respecto al eje x (por ejemplo, (−3, 7) está en el gráfico pero (−3, −7) no lo es)
La gráfica no es simétrica alrededor del eje y (por ejemplo, (−3, 7) está en la gráfica pero (3, 7) no lo es)
La gráfica no es simétrica sobre el origen (por ejemplo, (−3, 7) está en la gráfica pero (3, −7) no lo es)
- \(\ y=x^{3}-x\)
x-intercepta: (−1, 0), (0, 0), (1, 0)
intercepción en Y: (0, 0)
\(\ x\) \(\ y\) \(\ (x, y)\) −2 −6 (−2, −6) −1 0 (−1, 0) 0 0 (0, 0) 1 0 (1, 0) 2 6 (2, 6) 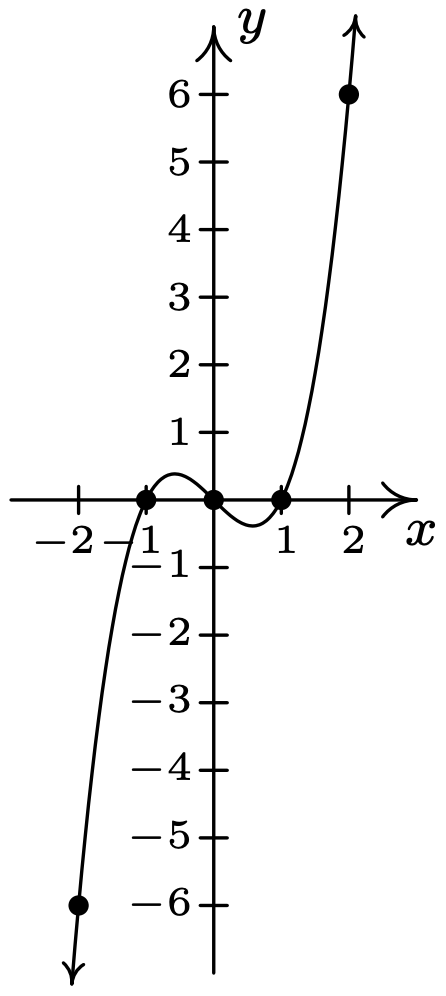
La gráfica no es simétrica con respecto al eje x. (por ejemplo, (2, 6) está en la gráfica pero (2, −6) no lo está)
La gráfica no es simétrica alrededor del eje y. (por ejemplo, (2, 6) está en la gráfica pero (−2, 6) no lo está)
La gráfica es simétrica sobre el origen.
- \(\ y=\frac{x^{3}}{4}-3 x\)
X-intercepta:\(\ (\pm 2 \sqrt{3}, 0),(0,0)\)
Intercepción en Y:\(\ (0, 0)\)
\(\ x\) \(\ y\) \(\ (x, y)\) −4 −4 \(\ (-4,-4)\) −3 \(\ \frac{9}{4}\) \(\ \left(-3, \frac{9}{4}\right)\) −2 4 (−2, 4) −1 \(\ \frac{11}{4}\) \(\ \left(-1, \frac{11}{4}\right)\) 0 0 (0, 0) 1 \(\ -\frac{11}{4}\) \(\ \left(1,-\frac{11}{4}\right)\) 2 −4 (2, -4) 3 \(\ -\frac{9}{4}\) \(\ \left(3,-\frac{9}{4}\right)\) 4 4 (4, 4) 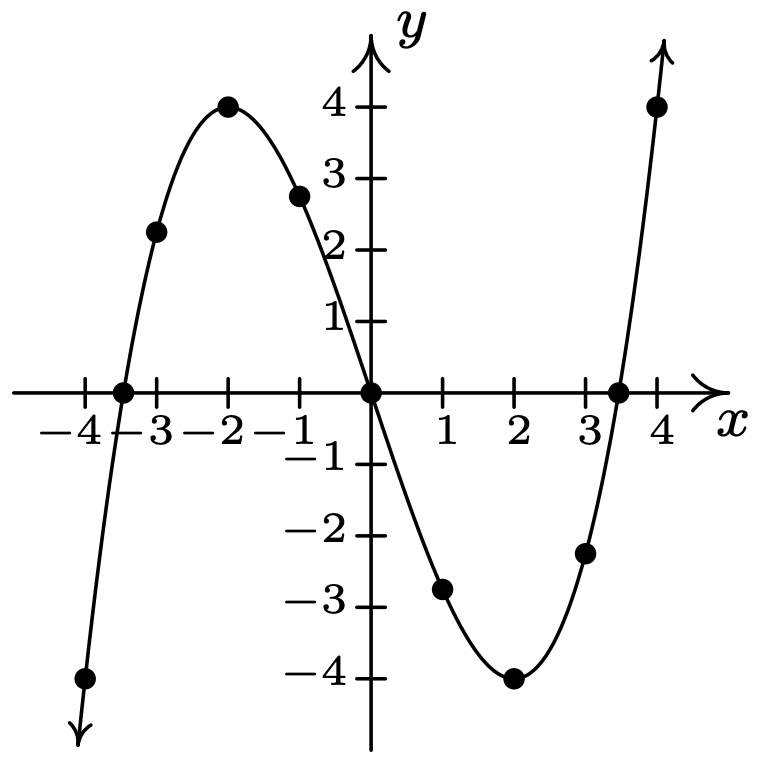
El gráfico no es simétrico con respecto al eje x (por ejemplo, (−4, −4) está en el gráfico pero (−4, 4) no lo es)
El gráfico no es simétrico alrededor del eje y (por ejemplo, (−4, −4) está en el gráfico pero (4, −4) no lo es)
La gráfica es simétrica sobre el origen
- \(\ y=\sqrt{x-2}\)
intercepción x: (2, 0)
La gráfica no tiene intercepciones en Y
\(\ x\) \(\ y\) \(\ (x, y)\) 2 0 (2, 0) 3 1 (3, 1) 6 2 (6, 2) 11 3 (11, 3) 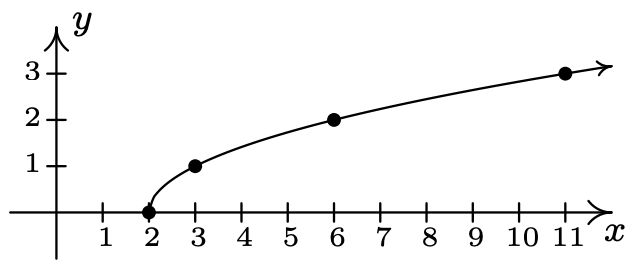
La gráfica no es simétrica con respecto al eje x (por ejemplo, (3, 1) está en la gráfica pero (3, −1) no lo es)
La gráfica no es simétrica alrededor del eje y (por ejemplo, (3, 1) está en la gráfica pero (−3, 1) no lo es)
La gráfica no es simétrica sobre el origen (por ejemplo, (3, 1) está en la gráfica pero (−3, −1) no lo es)
- \(\ y=2 \sqrt{x+4}-2\)
intercepción x: (−3, 0)
intercepción en Y: (0, 2)
\(\ x\) \(\ y\) \(\ (x, y)\) −4 −2 (−4, −2) −3 0 (−3, 0) −2 \(\ 2 \sqrt{2}-2\) \(\ (-2, \sqrt{2}-2)\) −1 \(\ 2 \sqrt{3}-2\) \(\ (-2, \sqrt{3}-2)\) 0 2 (0, 2) 1 \(\ 2 \sqrt{5}-2\) \ (\ (-2,\ sqrt {5} -2) 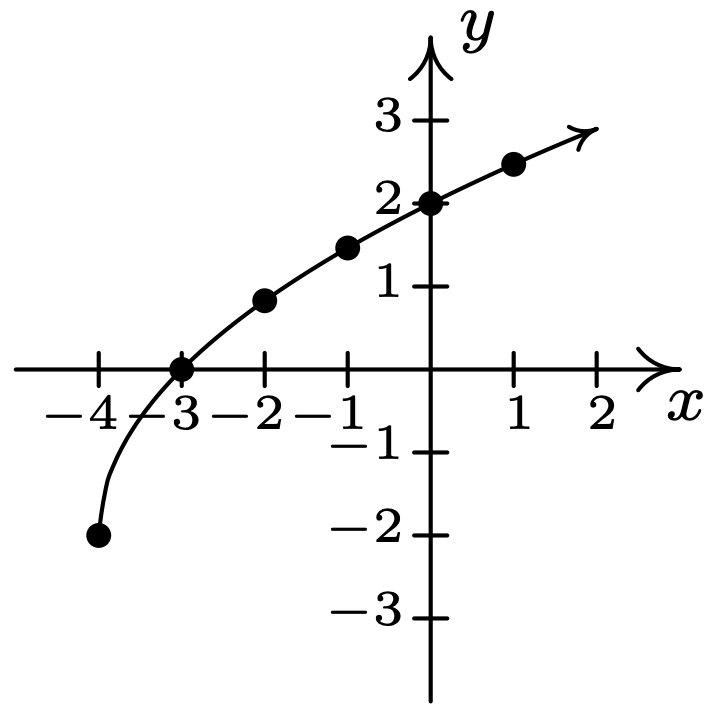
El gráfico no es simétrico con respecto al eje x (por ejemplo, (−4, −2) está en el gráfico pero (−4, 2) no lo es)
El gráfico no es simétrico alrededor del eje y (por ejemplo, (−4, −2) está en el gráfico pero (4, −2) no lo es)
La gráfica no es simétrica sobre el origen (por ejemplo, (−4, −2) está en la gráfica pero (4, 2) no lo es)
- \(\ 3 x-y=7\)
Reescribir como:\(\ y=3 x-7\).
X-intercepción:\(\ \left(\frac{7}{3}, 0\right)\)
intersección en Y: (0, −7)
\(\ x\) \(\ y\) \(\ (x, y)\) −2 −13 (−2, −13) −1 −10 (−1, −10) 0 −7 (0, −7) 1 −4 (1, −4) 2 −1 (2, −1) 3 2 (3, 2) 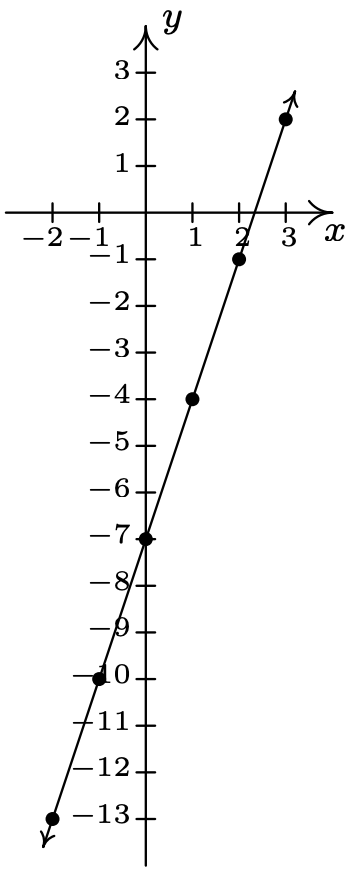
La gráfica no es simétrica con respecto al eje x (por ejemplo, (3, 2) está en la gráfica pero (3, −2) no lo es)
La gráfica no es simétrica alrededor del eje y (por ejemplo, (3, 2) está en la gráfica pero (−3, 2) no lo es)
La gráfica no es simétrica sobre el origen (por ejemplo, (3, 2) está en la gráfica pero (−3, −2) no lo es)
- \(\ 3 x-2 y=10\)
Reescribir como:\(\ y=\frac{3 x-10}{2}\).
X-intercepta:\(\ \left(\frac{10}{3}, 0\right)\)
Intercepción en Y:\(\ (0,-5)\)
\(\ x\) \(\ y\) \(\ (x, y)\) −2 −8 (−2, −8) −1 \(\ -\frac{13}{2}\) \(\ \left(-1,-\frac{13}{2}\right)\) 0 −5 (0, −5) 1 \(\ -\frac{7}{2}\) \(\ \left(1,-\frac{7}{2}\right)\) 2 −2 (2, −2) 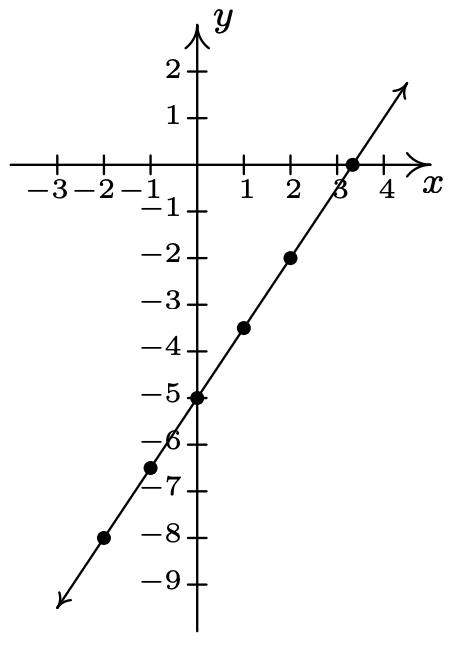
La gráfica no es simétrica con respecto al eje x (por ejemplo, (2, −2) está en la gráfica pero (2, 2) no lo es)
El gráfico no es simétrico alrededor del eje y (por ejemplo, (2, −2) está en el gráfico pero (−2, −2) no lo es)
La gráfica no es simétrica sobre el origen (por ejemplo, (2, −2) está en la gráfica pero (−2, 2) no lo es)
- \(\ (x+2)^{2}+y^{2}=16\)
Reescribir como\(\ y=\pm \sqrt{16-(x+2)^{2}}\).
X-intercepta:\(\ (−6, 0), (2, 0)\)
intercepta y:\(\ (0, \pm 2 \sqrt{3})\)
\(\ x\) \(\ y\) \(\ (x, y)\) −6 0 (−6, 0) −4 \(\ \pm 2 \sqrt{3}\) \(\ (-4, \pm 2 \sqrt{3})\) −2 \(\ \pm 4\) \(\ (-2, \pm 4)\) 0 \(\ \pm 2 \sqrt{3}\) \(\ (0, \pm 2 \sqrt{3})\) 2 0 (2, 0) 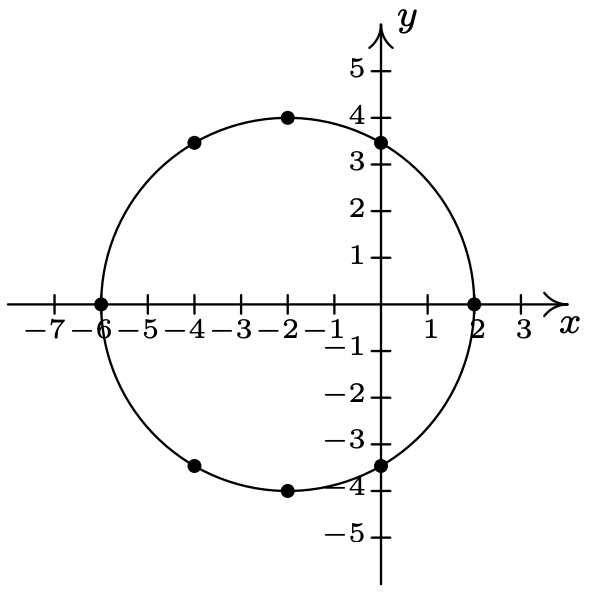
La gráfica es simétrica sobre el eje x
La gráfica no es simétrica con respecto al eje y (por ejemplo, (−6, 0) está en la gráfica pero (6, 0) no lo es)
La gráfica no es simétrica sobre el origen (por ejemplo, (−6, 0) está en la gráfica pero (6, 0) no lo es)
- \(\ x^{2}-y^{2}=1\)
Reescribir como:\(\ y=\pm \sqrt{x^{2}-1}\).
x-intercep: (−1, 0), (1, 0)
La gráfica no tiene intercepciones en Y
\(\ x\) \(\ y\) \(\ (x, y)\) −3 \(\ \pm \sqrt{8}\) \(\ (-3, \pm \sqrt{8})\) −2 \(\ \pm \sqrt{3}\) \(\ (-2, \pm \sqrt{3})\) −1 0 (−1, 0) 1 0 (1, 0) 2 \(\ \pm \sqrt{3}\) \(\ (2, \pm \sqrt{3})\) 3 \(\ \pm \sqrt{8}\) \(\ (3, \pm \sqrt{8})\) 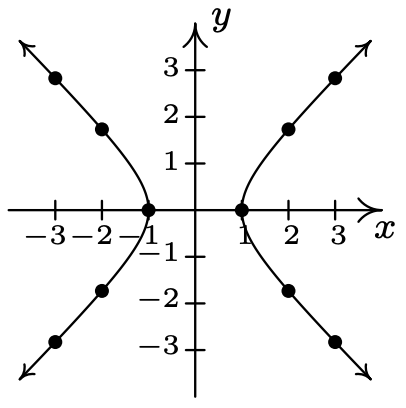
La gráfica es simétrica sobre el eje x
La gráfica es simétrica alrededor del eje y
La gráfica es simétrica sobre el origen
- \(\ 4 y^{2}-9 x^{2}=36\)
Reescribir como:\(\ y=\pm \frac{\sqrt{9 x^{2}+36}}{2}\).
La gráfica no tiene intercepciones x
intercepta y:\(\ (0, \pm 3)\)
\(\ x\) \(\ y\) \(\ (x, y)\) −4 \(\ \pm 3 \sqrt{5}\) \(\ (-4, \pm 3 \sqrt{5})\) −2 \(\ \pm 3 \sqrt{2}\) \(\ (-2, \pm 3 \sqrt{2})\) 0 \(\ \pm 3\) \(\ (0, \pm 3)\) 2 \(\ \pm 3 \sqrt{2}\) \(\ (2, \pm 3 \sqrt{2})\) 4 \(\ \pm 3 \sqrt{5}\) \(\ (4, \pm 3 \sqrt{5})\) 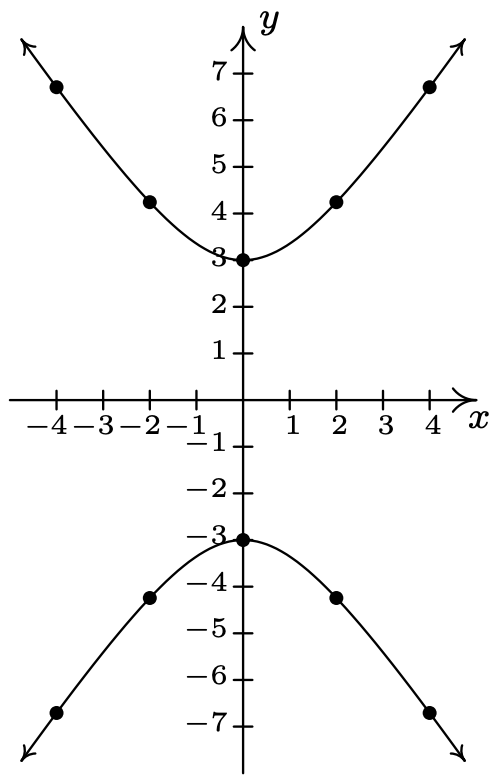
La gráfica es simétrica sobre el eje x
La gráfica es simétrica alrededor del eje y
La gráfica es simétrica sobre el origen
- \(\ x^{3} y=-4\)
Reescribir como:\(\ y=-\frac{4}{x^{3}}\).
La gráfica no tiene intercepciones x
La gráfica no tiene intercepciones en Y
\(\ x\) \(\ y\) \(\ (x, y)\) −2 \(\ \frac{1}{2}\) \(\ \left(-2, \frac{1}{2}\right)\) −1 4 \(\ (-1,4)\) \(\ -\frac{1}{2}\) 32 \(\ \left(-\frac{1}{2}, 32\right)\) \(\ \frac{1}{2}\) −32 \(\ \left(\frac{1}{2},-32\right)\) 1 −4 (1, −4) 2 \(\ -\frac{1}{2}\) \(\ \left(2,-\frac{1}{2}\right)\) 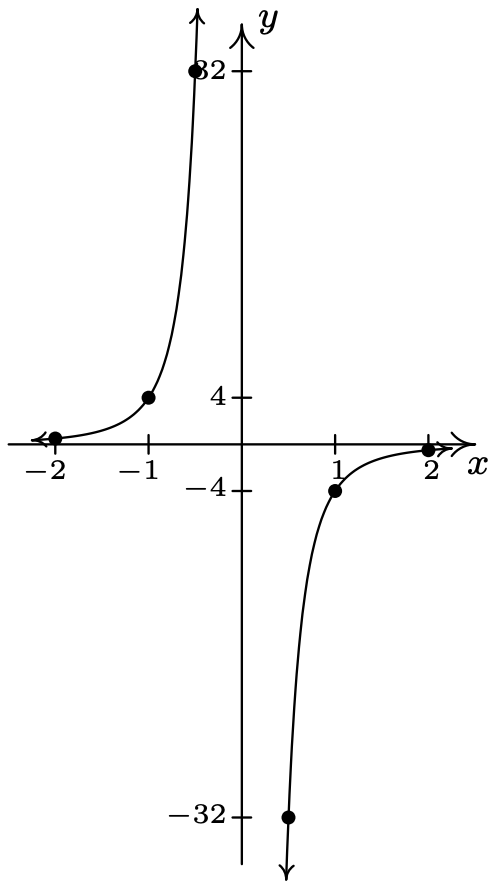
La gráfica no es simétrica con respecto al eje x (por ejemplo, (1, −4) está en la gráfica pero (1, 4) no lo es)
El gráfico no es simétrico alrededor del eje y (por ejemplo, (1, −4) está en el gráfico pero (−1, −4) no lo es)
La gráfica es simétrica sobre el origen
Referencia
1 Carl's, claro.
2 Realmente imposible. Se anima al lector interesado a investigar conjuntos contables versus incontables
3 Revisaremos el concepto de 'variable libre' en la Sección 8.1.
4 No te preocupes, ¡en un momento te refrescaremos la memoria sobre las líneas verticales y horizontales!
5 La palabra 'algunos' es un término relativo. Puede tomar 5, 10 o 50 puntos hasta que vea el patrón.
6 Sin el uso de una calculadora, ¡si puedes creerlo!