1.4: Notación de funciones

En la Definición 1.6, describimos una función como un tipo especial de relación\(-\) uno en el que cada\(x\) coordenada coincide con una sola\(y\) coordenada. En esta sección, nos centramos más en el proceso por el que\(x\) se empareja el con el\(y\). Si pensamos en el dominio de una función como un conjunto de entradas y el rango como un conjunto de salidas, podemos pensar en una función\(f\) como un proceso mediante el cual cada entrada\(x\) se empareja con una sola salida\(y\). Dado que la salida está completamente determinada por la entrada\(x\) y el proceso\(f\), simbolizamos la salida con notación de función:\(f(x)\) '', read '\(f\)of\(x\).' En otras palabras,\(f(x)\) es la salida que resulta aplicando el proceso\(f\) a la entrada\(x\). En este caso, los paréntesis aquí no indican multiplicación, como lo hacen en otras partes de Álgebra. Esto puede causar confusión si el contexto no es claro, por lo que debes leer atentamente. Esta relación se visualiza típicamente usando un diagrama similar al siguiente.

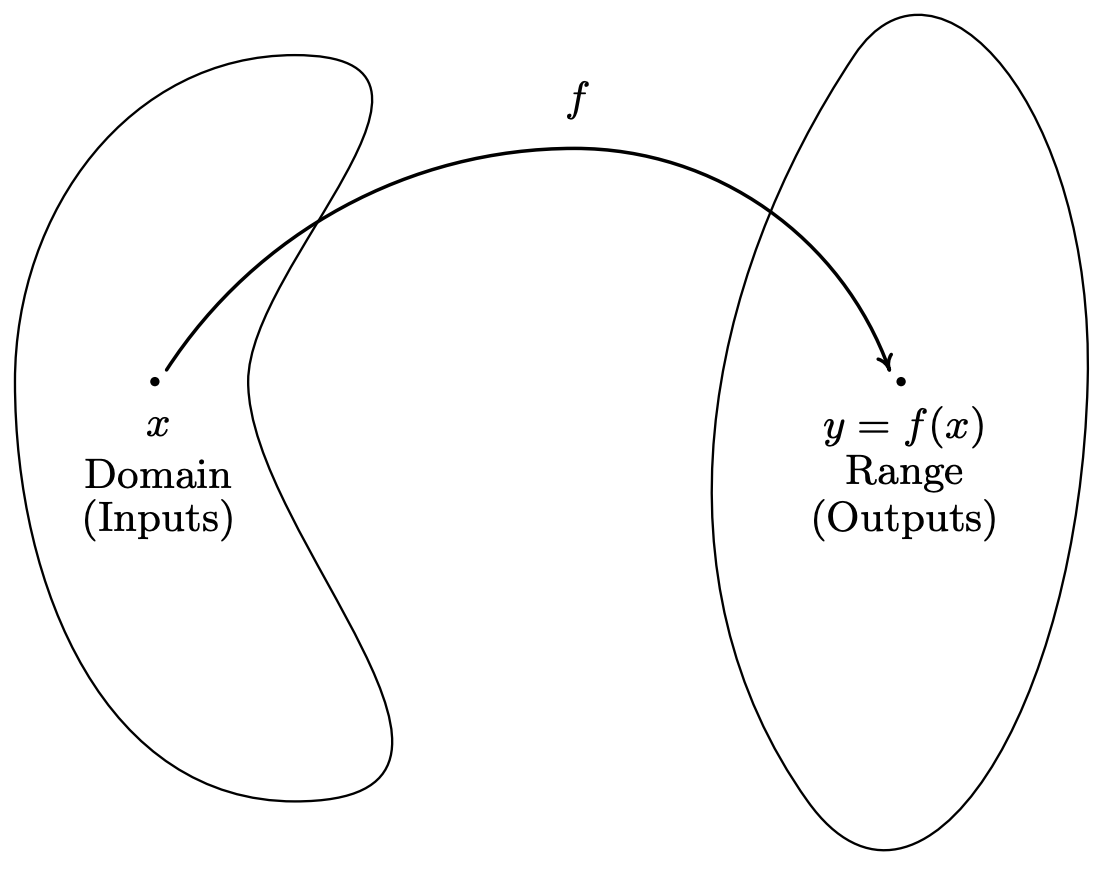
El valor de\(y\) depende completamente de la elección de\(x\). Por esta razón, a menudo\(x\) se llama la variable independiente, o argumento de\(f\), mientras que a menudo\(y\) se llama la variable dependiente. [argumento de función]

Como veremos, el proceso de una función\(f\) suele describirse usando una fórmula algebraica. Por ejemplo, supongamos que una función\(f\) toma un número real y realiza los dos pasos siguientes, en secuencia

1. multiplicar por 3
2. agregar 4

Si elegimos\(5\) como nuestro insumo, en el paso 1 multiplicamos por\(3\) para obtener\((5)(3) = 15\). En el paso 2, agregamos 4 a nuestro resultado del paso 1 que rinde\(15 + 4 = 19\). Usando la notación de funciones, escribiríamos\(f(5) = 19\) para indicar que el resultado de aplicar el proceso\(f\) a la entrada\(5\) da la salida\(19\). En general, si usamos\(x\) para la entrada, aplicando el paso 1 produce\(3x\). Siguiendo con el paso 2 produce\(3x+4\) como nuestra salida final. De ahí que para una entrada\(x\), obtenemos la salida\(f(x) = 3x + 4\). Observe que para verificar nuestra fórmula para el caso\(x=5\), reemplazamos la ocurrencia de\(x\) en la fórmula para por\(f(x)\)\(5\) obtener\(f(5) = 3(5) + 4 = 15 + 4 = 19\), según sea necesario.

Ejemplo 1.4.1

Supongamos que\(g\) se describe una función aplicando los siguientes pasos, en secuencia

1. agregar 4
2. multiplicar por 3

Determinar\(g(5)\) y encontrar una expresión para\(g(x)\).

Solución

Empezando con\(5\), el paso 1 da\(5+4 = 9\). Continuando con el paso 2, obtenemos\((3)(9) = 27\). Para encontrar una fórmula para\(g(x)\), comenzamos con nuestro aporte\(x\). El paso 1 produce\(x+4\). Ahora deseamos multiplicar esta cantidad entera por\(3\), así que usamos un paréntesis:\(3(x+4) = 3x + 12\). De ahí,\(g(x) = 3x + 12\). Podemos verificar nuestra fórmula reemplazando\(x\) con\(5\) para obtener\(g(5) = 3(5) + 12 = 15 + 12 = 27 \, \checkmark\).

La mayoría de las funciones que encontraremos en Álgebra Universitaria serán descritas usando fórmulas como las que desarrollamos para\(f(x)\) y\(g(x)\) superiores. Evaluar fórmulas usando esta notación de funciones es una habilidad clave para el éxito en este y muchos otros cursos de Matemáticas.

Ejemplo 1.4.2

Let\(f(x) = -x^2 + 3x + 4\)

1. Encuentre y simplifique lo siguiente.
   1. \(f(-1)\),\(f(0)\),\(f(2)\)
   2. \(f(2x)\),\(2 f(x)\)
   3. \(f(x+2)\),\(f(x)+2\),\(f(x) + f(2)\)
2. Resolver\(f(x) = 4\).

Solución.

1. 1. Para encontrar\(f(-1)\), reemplazamos cada ocurrencia de\(x\) en la expresión\(f(x)\) con\(-1\)

      \(\begin{array}{rclr} f(-1) & = & -(-1)^2 + 3(-1) + 4 & \\ & = & -(1) + (-3) + 4 & \\ & = & 0 & \\ \end{array}\)

      De igual manera\(f(0) = -(0)^2 + 3(0) + 4 = 4\),, y\(f(2) = -(2)^2 + 3(2) + 4 = -4+6+4 = 6\).

   2. Para encontrar\(f(2x)\), reemplazamos cada ocurrencia de\(x\) con la cantidad\(2x\)

      \(\begin{array}{rclr} f(2x) & = & -(2x)^2 + 3(2x) + 4 & \\ & = & -(4x^2) + (6x) + 4 & \\ & = & -4x^2+6x+4 & \\ \end{array}\)

      La expresión\(2f(x)\) significa que multiplicamos la expresión\(f(x)\) por\(2\)

      \(\begin{array}{rclr} 2f(x) & = & 2\left(-x^2 + 3x + 4\right) & \\ & = & -2x^2 + 6x + 8 \\ \end{array}\)

   3. Para encontrar\(f(x+2)\), reemplazamos cada ocurrencia de\(x\) con la cantidad\(x+2\)

      \(\begin{array}{rclr} f(x+2) & = & -(x+2)^2 + 3(x+2) + 4 & \\ & = & -\left(x^2 + 4x + 4\right) + (3x+6) + 4 & \\ & = & -x^2-4x-4+3x+6+4 & \\ & = & -x^2-x+6 & \end{array}\)

      Para encontrar\(f(x)+2\), agregamos\(2\) a la expresión para\(f(x)\)

      \(\begin{array}{rclr} f(x) + 2 & = & \left(-x^2 + 3x + 4\right) + 2 & \\ & = & -x^2 + 3x + 6 \\ \end{array}\)

      De nuestro trabajo anterior, vemos\(f(2) = 6\) así que

      \(\begin{array}{rclr} f(x) + f(2) & = & \left(-x^2 + 3x + 4\right) + 6 & \\ & = & -x^2 + 3x + 10 \\ \end{array}\)

2. Ya que\(f(x) = -x^2 + 3x + 4\), la ecuación\(f(x) = 4\) es equivalente a\(-x^2+3x+4 = 4\). Resolviendo obtenemos\(-x^2+3x = 0\), o\(x(-x+3) = 0\). Obtenemos\(x=0\) o\(x=3\), y podemos verificar estas respuestas comprobando eso\(f(0) = 4\) y\(f(3) = 4\).

Algunas notas sobre el Ejemplo 1.4.2 están en orden. Primero anote la diferencia entre las respuestas para\(f(2x)\) y\(2f(x)\). Porque\(f(2x)\), estamos multiplicando la entrada por\(2\); para\(2 f(x)\), estamos multiplicando la salida por\(2\). Como vemos, obtenemos resultados completamente diferentes. En esta línea, tenga en cuenta que\(f(x+2)\),\(f(x) + 2\) y\(f(x) + f(2)\) son tres expresiones diferentes también. Aunque la notación de funciones usa paréntesis, al igual que la multiplicación, no existe una 'propiedad distributiva' general de la notación de funciones. Finalmente, tenga en cuenta la práctica de usar paréntesis al sustituir una expresión algebraica por otra; recomendamos encarecidamente esta práctica ya que reducirá los errores descuidados.

Supongamos que ahora deseamos encontrar\(r(3)\) para\(r(x) = \frac{2x}{x^2 - 9}\). La sustitución da

\[r(3) = \dfrac{2(3)}{(3)^2-9} = \dfrac{6}{0},\]

que no está definido. (¿Por qué es esto, otra vez?) El número no\(3\) es una entrada permisible a la función\(r\); en otras palabras, no\(3\) está en el dominio de\(r\). ¿Qué otros números reales están prohibidos en esta fórmula? Pensamos de nuevo a la aritmética. La razón\(r(3)\) es indefinida es porque la sustitución da como resultado una división por\(0\). Para determinar qué otros números resultan en tal transgresión, establecemos el denominador igual a\(0\) y resolvemos

\[\begin{array}{rclr} x^2 - 9 & = & 0 & \\ x^2 & = & 9 & \\ \sqrt{x^2} & = & \sqrt{9} & \mbox{extract square roots} \\ x & = & \pm 3 & \\ \end{array}\]

Siempre y cuando sustituyamos números distintos de\(3\) y\(-3\), la expresión\(r(x)\) es un número real. De ahí que escribimos nuestro dominio en notación de intervalo ¹ como\((-\infty, -3) \cup (-3,3) \cup (3, \infty)\). Cuando se da una fórmula para una función, asumimos que la función es válida para todos los números reales que tienen sentido aritmético cuando se sustituye en la fórmula. Este conjunto de números a menudo se llama el dominio implícito ² de la función. En esta etapa, solo hay dos pecados matemáticos que debemos evitar: la división por\(0\) y la extracción de raíces pares de números negativos. El siguiente ejemplo ilustra estos conceptos.

Ejemplo 1.4.3

Encuentra el dominio ³ de las siguientes funciones.

1. \(g(x) = \sqrt{4 - 3x}\)
2. \(h(x) = \sqrt[5]{4 - 3x}\)
3. \(f(x) = \dfrac{2}{1 - \dfrac{4x}{x-3}}\)
4. \(F(x) = \dfrac{\sqrt[4]{2x+1}}{x^2-1}\)
5. \(r(t) = \dfrac{4}{6 - \sqrt{t+3}}\)
6. \(I(x) = \dfrac{3x^2}{x}\)

Solución

1. El desastre potencial para\(g\) es si el radicando ⁴ es negativo. Para evitar esto, nos fijamos\(4 - 3x \geq 0\). A partir de esto, obtenemos\(3x \leq 4\) o\(x \leq \frac{4}{3}\). Lo que esto muestra es que siempre y cuando\(x \leq \frac{4}{3}\), la expresión\(4 - 3x \geq 0\), y la fórmula\(g(x)\) devuelva un número real. Nuestro dominio es\(\left(-\infty, \frac{4}{3}\right]\).
2. La fórmula para\(h(x)\) es inquietantemente cercana a la de\(g(x)\) con una diferencia clave,\(-\) mientras que la expresión for\(g(x)\) incluye una raíz indexada par (es decir, una raíz cuadrada), la fórmula para\(h(x)\) implica una raíz indexada impar (la quinta raíz). Dado que las raíces impares de los números reales (números reales pares negativos) son números reales, no hay restricción en las entradas a\(h\). De ahí que el dominio sea\((-\infty, \infty)\).
3. En la expresión para\(f\), hay dos denominadores. Tenemos que asegurarnos de que ninguno de ellos lo sea\(0\). Para ello, establecemos cada denominador igual a\(0\) y resolvemos. Para el denominador 'pequeño', obtenemos\(x - 3 = 0\) o\(x=3\). Para el denominador 'grande'

   \[\begin{array}{rclr} 1 - \dfrac{4x}{x-3} & = & 0 & \\ 1 & = & \dfrac{4x}{x-3} & \\ (1)(x-3) & = & \left(\dfrac{4x}{\cancel{x-3}}\right)\cancel{(x-3)} & \mbox{clear denominators} \\ x - 3 & = & 4x & \\ -3 & = & 3x \\ -1 & = & x \end{array}\]

   Entonces obtenemos dos números reales que hacen denominadores\(0\), a saber\(x = -1\) y\(x=3\). Nuestro dominio es todo números reales excepto\(-1\) y\(3\):\((-\infty, -1) \cup (-1,3) \cup (3, \infty)\).

4. Al encontrar el dominio de\(F\), notamos que tenemos dos problemas potencialmente peligrosos: no solo tenemos un denominador, tenemos una cuarta raíz (indexada par). Nuestra estrategia es determinar las restricciones impuestas por cada parte y seleccionar los números reales que satisfagan ambas condiciones. Para satisfacer la cuarta raíz, requerimos\(2x+1 \geq 0\). De esto obtenemos\(2x \geq -1\) o\(x \geq -\frac{1}{2}\). A continuación, redondeamos los valores de los\(x\) cuales podrían causar problemas en el denominador al establecer el denominador igual a\(0\). Obtenemos\(x^2 - 1=0\), o\(x = \pm 1\). De ahí, para que un número\(x\) real esté en el dominio de\(F\),\(x \geq -\frac{1}{2}\) pero\(x \neq \pm 1\). En notación de intervalos, este conjunto es\(\left[ -\frac{1}{2}, 1 \right) \cup (1, \infty)\).
5. No se deje desanimado por el '\(t\)' aquí. Es una variable independiente que representa un número real, al igual que\(x\) lo hace, y está sujeta a las mismas restricciones. Como en el problema anterior, aquí tenemos doble peligro: tenemos una raíz cuadrada y un denominador. Para satisfacer la raíz cuadrada, necesitamos un radicando no negativo así que nos pusimos\(t + 3 \geq 0\) a obtener\(t \geq -3\). Establecer el denominador igual a cero da\(6 - \sqrt{t+3} =0\), o\(\sqrt{t+3} = 6\). Al cuadrar ambos lados da\(t+3 = 36\), o\(t = 33\). Dado que cuadramos ambos lados en el curso de resolver esta ecuación, necesitamos verificar nuestra respuesta. ⁵ Efectivamente, cuando\(t=33\)\(6 - \sqrt{t+3} = 6 - \sqrt{36} = 0\), así\(t=33\) causará problemas en el denominador. Por fin podemos encontrar el dominio de\(r\): necesitamos\(t \geq -3\), pero\(t \neq 33\). Nuestra respuesta final es\([-3, 33) \cup (33, \infty)\).
6. Es tentador simplificar\(I(x) = \frac{3x^2}{x} = 3x\), y, como ya no hay denominadores, afirmar que ya no hay restricciones. No obstante, al simplificar\(I(x)\), estamos asumiendo\(x \neq 0\), ya que\(\frac{0}{0}\) es indefinido. ⁶ Procediendo como antes, encontramos que el dominio de\(I\) ser todos los números reales excepto\(0\):\((-\infty, 0) \cup (0, \infty)\).

Cabe reiterar la importancia de encontrar el dominio de una función antes de simplificarla, como lo demuestra la función\(I\) en el ejemplo anterior. A pesar de que la fórmula se\(I(x)\) simplifica a\(3x\), sería inexacto escribir\(I(x) = 3x\) sin agregar la estipulación de que\(x \neq 0\). Sería análogo a no reportar ingresos imponibles o algún otro pecado de omisión.

1.4.1 Modelado con Funciones

La importancia de las Matemáticas para nuestra sociedad radica en su valor para aproximar, o modelar fenómenos del mundo real. Ya sea que se utilice para predecir la alta temperatura en un día determinado, determinar las horas de luz del día en un día determinado, o predecir tendencias poblacionales de diversas y diversas bestias reales y míticas, ⁷ Las matemáticas solo son superadas por la alfabetización en la importancia del desarrollo de la humanidad. ⁸

Es importante tener en cuenta que cada vez que las Matemáticas se utilizan para aproximar la realidad, siempre hay limitaciones para el modelo. Por ejemplo, supongamos que las uvas están a la venta en el mercado local\(\$1.50\) por libra. Entonces cuesta una libra de uvas\(\$1.50\), dos libras de uvas cuestan\(\$3.00\), y así sucesivamente. Supongamos que queremos desarrollar una fórmula que relacione el costo de comprar uvas con la cantidad de uvas que se compran. Dado que estas dos cantidades varían de una situación a otra, les asignamos variables. Dejar\(c\) denotar el costo de las uvas y dejar\(g\) denotar la cantidad de uvas compradas. Para encontrar el costo\(c\) de las uvas, multiplicamos la cantidad de uvas\(g\) por el precio\(\$1.50\) dólares por libra para obtener\[c = 1.5 g\] Para que las unidades sean correctas en la fórmula,\(g\) deben medirse en libras de uva en cuyo caso el valor calculado de \(c\)se mide en dólares. Dado que estamos interesados en encontrar el costo\(c\) dado un monto\(g\), pensamos en\(g\) como la variable independiente y\(c\) como la variable dependiente. Usando el lenguaje de notación de funciones, escribimos\[c(g) = 1.5 g\] dónde\(g\) está la cantidad de uvas compradas (en libras) y\(c(g)\) es el costo (en dólares). Por ejemplo,\(c(5)\) representa el costo, en dólares, de comprar\(5\) libras de uva. En este caso,\(c(5) = 1.5(5) = 7.5\), por lo que costaría\(\$ 7.50\). Si, por otro lado, quisiéramos encontrar la cantidad de uvas para las que podemos comprar\(\$5\), tendríamos que fijar\(c(g) = 5\) y resolver\(g\). En este caso,\(c(g)=1.5g\), por lo que resolver\(c(g) = 5\) equivale a resolver\(1.5g = 5\) Hacerlo da\(g = \frac{5}{1.5} = 3.\overline{3}\). Esto significa que podemos comprar exactamente\(3.\overline{3}\) libras de uvas para\(\$5\). Por supuesto, sería difícil comprar exactamente\(3.\overline{3}\) libras de uvas, ⁹ y esto nos lleva a nuestro siguiente tema de discusión, el dominio aplicado ¹⁰ de una función.

A pesar de que, matemáticamente, no\(c(g) = 1.5g\) tiene restricciones de dominio (no hay denominadores y no hay radicales pares indexados), hay ciertos valores de\(g\) que no tienen ningún sentido físico. Por ejemplo,\(g = -1\) corresponde a 'comprar'\(-1\) libras de uvas. ¹¹ Además, a menos que el 'mercado local' mencionado sea el Estado de California (o algún otro exportador de uvas), tampoco tiene mucho sentido para\(g = 500,\!000,\!000\), tampoco. Entonces la realidad de la situación limita lo que\(g\) puede ser, y estos límites determinan el dominio aplicado de\(g\). Por lo general, un dominio aplicado se establece explícitamente. En este caso, sería común ver algo así como\(c(g) = 1.5g\),, es decir\(0 \leq g \leq 100\), el número de libras de uva compradas está limitado de\(0\) hasta\(100\). El límite superior aquí,\(100\) puede representar el inventario del mercado, o algún otro límite establecido por la política o ley local. Incluso con esta restricción, nuestro modelo tiene sus limitaciones. Como vimos anteriormente, es prácticamente imposible comprar exactamente\(3.\overline{3}\) libras de uva para que nuestro costo sea exactamente\(\$5\). En este caso, siendo compradores sensatos, lo más probable es que 'redondear' y compraríamos\(3\) libras de uva o sin embargo cerraríamos la escala del mercado con la que se pueda leer\(3.\overline{3}\) sin haber terminado. Es hora de un ejemplo más sofisticado.

Ejemplo 1.4.4

La altura\(h\) en pies de un cohete modelo sobre el suelo\(t\) segundos después del despegue viene dada por\[h(t) = \left\{ \begin{array}{rcl} -5t^2 + 100t, & \mbox{if} & 0 \leq t \leq 20 \\ 0, & \mbox{if} & t > 20 \\ \end{array} \right.\]

1. Encontrar e interpretar\(h(10)\) y\(h(60)\).
2. Resuelve\(h(t) = 375\) e interpreta tus respuestas.

Solución.

1. Primero notamos que la variable independiente aquí es\(t\), elegida porque representa el tiempo. En segundo lugar, la función se divide en dos reglas: una fórmula para valores de\(t\) entre\(0\) e\(20\) inclusive, y otra para valores\(t\) mayores de 20. Ya que\(t=10\) satisface la desigualdad\(0 \leq t \leq 20\), utilizamos la primera fórmula listada,\(h(t) = -5t^2 + 100t\), para encontrar\(h(10)\). Obtenemos\(h(10) = -5(10)^2 + 100(10) = 500\). Dado que\(t\) representa el número de segundos desde el despegue y\(h(t)\) es la altura sobre el suelo en pies, la ecuación\(h(10) = 500\) significa que\(10\) segundos después del despegue, el cohete modelo se encuentra a\(500\) pies sobre el suelo. Para encontrar\(h(60)\), observamos que\(t=60\) satisface\(t > 20\), por lo que utilizamos la regla\(h(t) = 0\). Esta función devuelve un valor de\(0\) independientemente del valor que se sustituya en\(t\), entonces\(h(60) = 0\). Esto quiere decir que\(60\) segundos después del despegue, el cohete se encuentra a\(0\) pies sobre el suelo; es decir, un minuto después del despegue, el cohete ya ha regresado a la Tierra.
2. Dado que la función\(h\) se define en piezas, necesitamos resolverla\(h(t) = 375\) en pedazos. Para\(0 \leq t \leq 20\),\(h(t) = -5t^2 + 100t\), así para estos valores de\(t\), resolvemos\(-5t^2 + 100t = 375\). Reordenando términos, obtenemos\(5t^2 - 100t + 375 = 0\), y factoring da\(5(t-5)(t-15) = 0\). Nuestras respuestas son\(t=5\) y\(t=15\), y dado que ambos valores de\(t\) mentira entre\(0\) y\(20\), mantenemos ambas soluciones. Para\(t>20\),\(h(t) = 0\), y en este caso, no hay soluciones para\(0=375\). En cuanto al cohete modelo, resolver\(h(t) = 375\) corresponde a encontrar cuándo, si alguna vez, el cohete alcanza\(375\) pies sobre el suelo. Nuestras dos respuestas,\(t=5\) y\(t=15\) corresponden a que el cohete alcanza esta altitud dos veces, una vez\(5\) segundos después del lanzamiento, y nuevamente\(15\) segundos después del lanzamiento. ¹²

El tipo de función en el ejemplo anterior se llama una función definida por partes, o función 'por partes' para abreviar. Muchos fenómenos del mundo real, las fórmulas del impuesto sobre la renta ¹³ por ejemplo, son modelados por tales funciones.

Por cierto, si quisiéramos evitar usar una función por partes en el Ejemplo 1.4.4, podríamos haber usado\(h(t) = -5t^2 + 100t\) en el dominio explícito\(0 \leq t \leq 20\) porque después de 20 segundos, el cohete está en el suelo y deja de moverse. En muchos casos, sin embargo, las funciones por partes son su única opción, por lo que es mejor entenderlas bien.

El modelado matemático no es un tema de una sección. Ni siquiera es un tema de un solo curso como lo demuestran los cursos de pregrado y posgrado en modelación matemática que se ofrecen en muchas universidades. Por lo tanto, nuestro objetivo en esta sección no puede ser el de contarte toda la historia. Lo que podemos hacer es que empiezas. A medida que estudiemos nuevas clases de funciones, veremos qué fenómenos se pueden utilizar para modelar. En ese sentido, la modelación matemática no puede ser un tema en un libro, sino más bien, debe ser un tema del libro. Por ahora, te tenemos explorando algunos modelos muy básicos en los Ejercicios porque necesitas gatear para caminar para correr. A medida que aprendamos más sobre las funciones, te ayudaremos a construir tus propios modelos y ponerte en camino de aplicar las Matemáticas a tu mundo.

1.4.2 Ejercicios

En los Ejercicios 1-10, encuentra una expresión para\(f(x)\) y declara su dominio.

1. \(f\)es una función que toma un número real\(x\) y realiza los siguientes tres pasos en el orden dado: (1) multiplicar por 2; (2) sumar 3; (3) dividir por 4.
2. \(f\)es una función que toma un número real\(x\) y realiza los siguientes tres pasos en el orden dado: (1) sumar 3; (2) multiplicar por 2; (3) dividir por 4.
3. \(f\)es una función que toma un número real\(x\) y realiza los siguientes tres pasos en el orden dado: (1) dividir por 4; (2) sumar 3; (3) multiplicar por 2.
4. \(f\)es una función que toma un número real\(x\) y realiza los siguientes tres pasos en el orden dado: (1) multiplicar por 2; (2) sumar 3; (3) tomar la raíz cuadrada.
5. \(f\)es una función que toma un número real\(x\) y realiza los siguientes tres pasos en el orden dado: (1) sumar 3; (2) multiplicar por 2; (3) tomar la raíz cuadrada.
6. \(f\)es una función que toma un número real\(x\) y realiza los siguientes tres pasos en el orden dado: (1) sumar 3; (2) tomar la raíz cuadrada; (3) multiplicar por 2.
7. \(f\)es una función que toma un número real\(x\) y realiza los siguientes tres pasos en el orden dado: (1) tomar la raíz cuadrada; (2) restar 13; (3) hacer de la cantidad el denominador de una fracción con el numerador 4.
8. \(f\)es una función que toma un número real\(x\) y realiza los siguientes tres pasos en el orden dado: (1) restar 13; (2) tomar la raíz cuadrada; (3) hacer de la cantidad el denominador de una fracción con el numerador 4.
9. \(f\)es una función que toma un número real\(x\) y realiza los siguientes tres pasos en el orden dado: (1) tomar la raíz cuadrada; (2) hacer de la cantidad el denominador de una fracción con el numerador 4; (3) restar 13.
10. \(f\)es una función que toma un número real\(x\) y realiza los siguientes tres pasos en el orden dado: (1) hacer de la cantidad el denominador de una fracción con el numerador 4; (2) tomar la raíz cuadrada; (3) restar 13.

En los Ejercicios 11-18, utilice la función dada\(f\) para encontrar y simplificar lo siguiente:

• \(f(3)\)
• \(f(-1)\)
• \(f\left(\frac{3}{2} \right)\)
• \(f(4x)\)
• \(4f(x)\)
• \(f(-x)\)
• \(f(x-4)\)
• \(f(x) - 4\)
• \(f\left(x^2\right)\)

11. \(f(x) = 2x+1\)
12. \(f(x) = 3 - 4x\)
13. \(f(x) = 2 - x^2\)
14. \(f(x) = x^2 - 3x + 2\)
15. \(f(x) = \dfrac{x}{x-1}\)
16. \(f(x) = \dfrac{2}{x^{3}}\)
17. \(f(x) = 6\)
18. \(f(x) = 0\)

En los Ejercicios 19-26, utilice la función dada\(f\) para encontrar y simplificar lo siguiente:

• \(f(2)\)
• \(f(-2)\)
• \(f(2a)\)
• \(2 f(a)\)
• \(f(a+2)\)
• \(f(a) + f(2)\)
• \(f \left( \frac{2}{a} \right)\)
• \(\frac{f(a)}{2}\)
• \(f(a + h)\)

19. \(f(x) = 2x-5\)
20. \(f(x) = 5-2x\)
21. \(f(x) = 2x^2 - 1\)
22. \(f(x) = 3x^2+3x-2\)
23. \(f(x) = \sqrt{2x+1}\)
24. \(f(x) = 117\)
25. \(f(x) = \dfrac{x}{2}\)
26. \(f(x) = \dfrac{2}{x}\)

En los Ejercicios 27-34, usa la función dada\(f\) para encontrar\(f(0)\) y resolver\(f(x) = 0\)

27. \(f(x) = 2x - 1\)
28. \(f(x) = 3 - \frac{2}{5} x\)
29. \(f(x) = 2x^2 - 6\)
30. \(f(x) = x^2 - x - 12\)
31. \(f(x) = \sqrt{x+4}\)
32. \(f(x) = \sqrt{1-2x}\)
33. \(f(x) = \dfrac{3}{4-x}\)
34. \(f(x) = \dfrac{3x^2-12x}{4-x^2}\)
35. Vamos\(f(x) = \left\{ \begin{array}{rcr} x + 5 & \mbox{ if } & x \leq -3 \\ \sqrt{9-x^2} & \mbox{ if } & -3 < x \leq 3 \\ -x+5 & \mbox{ if } & x > 3 \\ \end{array} \right.\) Calcular los siguientes valores de función.
    1. \(f(-4)\)
    2. \(f(-3)\)
    3. \(f(3)\)
    4. \(f(3.001)\)
    5. \(f(-3.001)\)
    6. \(f(2)\)
36. Vamos\({\displaystyle f(x) = \left\{ \begin{array}{rcr} x^{2} & \mbox{ if } & x \leq -1\\ \sqrt{1 - x^{2}} & \mbox{ if } & -1 < x \leq 1\\ x & \mbox{ if } & x > 1 \end{array} \right. }\) Calcular los siguientes valores de función.
    1. \(f(4)\)
    2. \(f(-3)\)
    3. \(f(1)\)
    4. \(f(0)\)
    5. \(f(-1)\)
    6. \(f(-0.999)\)

En los Ejercicios 37-62, encuentra el dominio (implícito) de la función.

37. \(f(x) = x^{4} - 13x^{3} + 56x^{2} - 19\)
38. \(f(x) = x^2 + 4\)
39. \(f(x) = \dfrac{x-2}{x+1}\)
40. \(f(x) = \dfrac{3x}{x^2+x-2}\)
41. \(f(x) = \dfrac{2x}{x^2+3}\)
42. \(f(x) = \dfrac{2x}{x^2-3}\)
43. \(f(x) = \dfrac{x+4}{x^2 - 36}\)
44. \(f(x) = \dfrac{x-2}{x-2}\)
45. \(f(x) = \sqrt{3-x}\)
46. \(f(x) = \sqrt{2x+5}\)
47. \(f(x) = 9x\sqrt{x+3}\)
48. \(f(x) = \dfrac{\sqrt{7-x}}{x^2+1}\)
49. \(f(x) = \sqrt{6x-2}\)
50. \(f(x) = \dfrac{6}{\sqrt{6x-2}}\)
51. \(f(x) = \sqrt[3]{6x-2}\)
52. \(f(x) = \dfrac{6}{4 - \sqrt{6x-2}}\)
53. \(f(x) = \dfrac{\sqrt{6x-2}}{x^2-36}\)
54. \(f(x) = \dfrac{\sqrt[3]{6x-2}}{x^2+36}\)
55. \(s(t) = \dfrac{t}{t - 8}\)
56. \(Q(r) = \dfrac{\sqrt{r}}{r - 8}\)
57. \(b(\theta) = \dfrac{\theta}{\sqrt{\theta - 8}}\)
58. \(A(x) = \sqrt{x - 7} + \sqrt{9 - x}\)
59. \(\alpha(y) = \sqrt[3]{\dfrac{y}{y - 8}}\)
60. \(g(v) = \dfrac{1}{4 - \dfrac{1}{v^{2}}}\)
61. \(T(t) = \dfrac{\sqrt{t} - 8}{5-t}\)
62. \(u(w) = \dfrac{w - 8}{5 - \sqrt{w}}\)
63. El área\(A\) encerrada por un cuadrado, en pulgadas cuadradas, es función de la longitud de uno de sus lados\(x\), cuando se mide en pulgadas. Esta relación se expresa por la fórmula\(A(x) = x^2\) para\(x > 0\). Encuentra\(A(3)\) y resuelve\(A(x) = 36\). Interpreta tus respuestas a cada uno. ¿Por qué se\(x\) restringe a\(x > 0\)?
64. El área\(A\) encerrada por un círculo, en metros cuadrados, es función de su radio\(r\), cuando se mide en metros. Esta relación se expresa por la fórmula\(A(r) = \pi r^2\) para\(r > 0\). Encuentra\(A(2)\) y resuelve\(A(r) = 16\pi\). Interpreta tus respuestas a cada uno. ¿Por qué se\(r\) restringe a\(r > 0\)?
65. El volumen\(V\) encerrado por un cubo, en centímetros cúbicos, es función de la longitud de uno de sus lados\(x\), cuando se mide en centímetros. Esta relación se expresa por la fórmula\(V(x) = x^3\) para\(x > 0\). Encuentra\(V(5)\) y resuelve\(V(x) = 27\). Interpreta tus respuestas a cada uno. ¿Por qué se\(x\) restringe a\(x > 0\)?
66. El volumen\(V\) encerrado por una esfera, en pies cúbicos, es una función del radio de la esfera\(r\), cuando se mide en pies. Esta relación se expresa por la fórmula\(V(r) =\frac{4\pi}{3} r^{3}\) para\(r > 0\). Encuentra\(V(3)\) y resuelve\(V(r) = \frac{32\pi}{3}\). Interpreta tus respuestas a cada uno. ¿Por qué se\(r\) restringe a\(r > 0\)?
67. La altura de un objeto caído del techo de un edificio de ocho pisos está modelada por:\(h(t) = -16t^2 + 64\),\(0 \leq t \leq 2\). Aquí,\(h\) es la altura del objeto del suelo, en pies,\(t\) segundos después de que el objeto se haya caído. Encuentra\(h(0)\) y resuelve\(h(t) = 0\). Interpreta tus respuestas a cada uno. ¿Por qué se\(t\) restringe a\(0 \leq t \leq 2\)?
68. La temperatura\(T\) en grados Fahrenheit\(t\) horas después de las 6 AM es dada por\(T(t) = -\frac{1}{2} t^2 + 8t+3\) for\(0 \leq t \leq 12\). Encontrar e interpretar\(T(0)\),\(T(6)\) y\(T(12)\).
69. La función\(C(x) = x^2-10x+27\) modela el costo, en cientos de dólares, para producir\(x\) mil bolígrafos. Encontrar e interpretar\(C(0)\),\(C(2)\) y\(C(5)\).
70. Utilizando datos de la Oficina de Estadísticas de Transporte,, la economía de combustible promedio\(F\) en millas por galón para los turismos en Estados Unidos puede ser modelada por\(F(t) = -0.0076t^2+0.45t + 16\),\(0 \leq t \leq 28\), donde\(t\) es el número de años transcurridos desde\(1980\). Usa tu calculadora para encontrar\(F(0)\),\(F(14)\) y\(F(28)\). Redondea tus respuestas a dos decimales e interpreta tus respuestas a cada una.
71. La población de Sasquatch en el condado de Portage puede ser modelada por la función\(P(t) = \frac{150t}{t + 15}\), donde\(t\) representa el número de años desde 1803. Encontrar e interpretar\(P(0)\) y\(P(205)\). Discuta con sus compañeros de clase cuál\(P\) debe ser el dominio aplicado y el rango de.
72. Para\(n\) copias del libro Me and my Sasquatch, una compañía de impresión bajo demanda cobra\(C(n)\) dólares, donde\(C(n)\) se determina por la fórmula\[{\displaystyle C(n) = \left\{ \begin{array}{rcl} 15n & \mbox{ if } & 1 \leq n \leq 25 \\ 13.50n & \mbox{ if } & 25 < n \leq 50 \\ 12n & \mbox{ if } & n > 50 \\ \end{array} \right. }\]
    1. Encontrar e interpretar\(C(20)\).
    2. [50vs51] ¿Cuánto cuesta pedir 50 copias del libro? ¿Qué pasa con 51 copias?
    3. Tu respuesta al 72b debería hacerte pensar. Supongamos que una librería estima que venderá 50 ejemplares del libro. ¿Cuántos libros se pueden pedir, de hecho, por el mismo precio que esos 50 ejemplares? (Redondea tu respuesta a un número entero de libros.)
73. Un minorista de cómics en línea cobra los costos de envío de acuerdo con la siguiente fórmula\[{\displaystyle S(n) = \left\{ \begin{array}{rcl} 1.5 n + 2.5 & \mbox{ if } & 1 \leq n \leq 14 \\ 0 & \mbox{ if } & n \geq 15 \end{array} \right. }\]
    1. ¿Cuál es el costo de enviar 10 cómics?
    2. ¿Cuál es el significado de la fórmula\(S(n) = 0\)\(n \geq 15\)?
74. [piecewisemobile] El costo\(C\) (en dólares) para hablar\(m\) minutos al mes en un plan de telefonía móvil está modelado por\[{\displaystyle C(m) = \left\{ \begin{array}{rcl} 25 & \mbox{ if } & 0 \leq m \leq 1000 \\ 25+0.1(m-1000) & \mbox{ if } & m > 1000 \end{array} \right. }\]
    1. ¿Cuánto cuesta platicar\(750\) minutos mensuales con este plan?
    2. ¿Cuánto cuesta platicar\(20\) horas al mes con este plan?
    3. Explique verbalmente los términos del plan.
75. En la Sección 1.1.1 definimos el conjunto de enteros como\(\mathbb{Z} = \{ \ldots, -3, -2, -1, 0, 1, 2, 3, \ldots\}\). ¹⁴ El mayor número entero de, denotado por\(\lfloor x \rfloor\), se define como el entero más grande\(k\) con\(k \leq x\).
    1. Buscar\(\lfloor 0.785 \rfloor\),\(\lfloor 117 \rfloor\),\(\lfloor -2.001 \rfloor\), y\(\lfloor \pi + 6 \rfloor\)
    2. Discuta con sus compañeros de clase cómo\(\lfloor x \rfloor\) puede describirse como una función definida por partes.

       SUMINACIÓN: ¡Hay infinitamente muchas piezas!

    3. ¿\(\lfloor a + b \rfloor = \lfloor a \rfloor + \lfloor b \rfloor\)Siempre es verdad? ¿Qué pasa si\(a\) o\(b\) es un número entero? Pon a prueba algunos valores, haz una conjetura y explica tu resultado.
76. Hemos intentado a través de nuestros ejemplos convencerte de que, en general,\(f(a + b) \neq f(a) + f(b)\). Ha sido nuestra experiencia que los estudiantes se niegan a creernos así que volveremos a intentarlo con un enfoque diferente. Con la ayuda de tus compañeros de clase, encuentra una función\(f\) para la que siempre sean ciertas las siguientes propiedades.
    1. \(f(0) = f(-1 + 1) = f(-1) + f(1)\)
    2. \(f(5) = f(2 + 3) = f(2) + f(3)\)
    3. \(f(-6) = f(0 - 6) = f(0) - f(6)\)
    4. \(f(a + b) = f(a) + f(b)\;\)independientemente de los dos números que le demos\(a\) y\(b\).

    ¿Cuántas funciones encontraste que no cumplieron con las condiciones anteriores? ¿\(f(x) = x^{2}\)Funcionó? ¿Qué pasa\(f(x) = \sqrt{x}\) con o\(f(x) = 3x + 7\) o\(f(x) = \dfrac{1}{x}\)? ¿Encontraste algún atributo común a aquellas funciones que sí tuvieron éxito? Deberías haberlo hecho, porque solo hay una familia extremadamente especial de funciones que realmente funciona aquí. Así volvemos a nuestra declaración anterior, en general,\(f(a + b) \neq f(a) + f(b)\).

RESPUESTAS

1. \(f(x) = \frac{2x+3}{4}\)
   Dominio:\((-\infty, \infty)\)

2. \(f(x) = \frac{2(x+3)}{4} = \frac{x+3}{2}\)
   Dominio:\((-\infty, \infty)\)

3. \(f(x) = 2\left(\frac{x}{4} + 3\right) = \frac{1}{2} x + 6\)
   Dominio:\((-\infty, \infty)\)

4. \(f(x) = \sqrt{2x+3}\)
   Dominio:\(\left[ -\frac{3}{2}, \infty \right)\)

5. \(f(x) = \sqrt{2(x+3)} = \sqrt{2x+6}\)
   Dominio:\([-3, \infty)\)

6. \(f(x) = 2\sqrt{x+3}\)
   Dominio:\([-3, \infty)\)

7. \(f(x) = \frac{4}{\sqrt{x} - 13}\)
   Dominio:\([0, 169) \cup (169, \infty)\)

8. \(f(x) = \frac{4}{\sqrt{x - 13}}\)
   Dominio:\((13, \infty)\)

9. \(f(x) = \frac{4}{\sqrt{x}} - 13\)
   Dominio:\((0, \infty)\)

10. \(f(x) = \sqrt{\frac{4}{x}} - 13 = \frac{2}{\sqrt{x}} - 13\)
    Dominio:\((0, \infty)\)

11. Para\(f(x) = 2x+1\)
    • \(f(3) = 7\)
    • \(f(-1) = -1\)
    • \(f\left(\frac{3}{2} \right) = 4\)
    • \(f(x-4) = 2x-7\)
    • \(f(x) - 4 = 2x-3\)
    • \(f\left(x^2\right) = 2x^2+1\)
    • \(f(4x) = 8x+1\)
    • \(4f(x) = 8x+4\)
    • \(f(-x) = -2x+1\)
12. Para\(f(x) = 3-4x\)
    • \(f(3) = -9\)
    • \(f(-1) = 7\)
    • \(f\left(\frac{3}{2} \right) = -3\)
    • \(f(x-4) = 19-4x\)
    • \(f(x) - 4 = -4x-1\)
    • \(f\left(x^2\right) = 3-4x^2\)
    • \(f(4x) = 3-16x\)
    • \(4f(x) = 12-16x\)
    • \(f(-x) = 4x+3\)
13. Para\(f(x) = 2 - x^2\)
    • \(f(3) = -7\)
    • \(f(-1) = 1\)
    • \(f\left(\frac{3}{2} \right) = -\frac{1}{4}\)
    • \(f(x-4) = -x^2+8x-14\)
    • \(f(x) - 4 = -x^{2} - 2\)
    • \(f\left(x^2\right) = 2-x^4\)
    • \(f(4x) = 2-16x^2\)
    • \(4f(x) = 8-4x^2\)
    • \(f(-x) = 2-x^2\)
14. Para\(f(x) = x^2 - 3x + 2\)
    • \(f(3) = 2\)
    • \(f(-1) = 6\)
    • \(f\left(\frac{3}{2} \right) = -\frac{1}{4}\)
    • \(f(x-4) = x^2-11x+30\)
    • \(f(x) - 4 = x^2-3x-2\)
    • \(f\left(x^2\right) = x^4-3x^2+2\)
    • \(f(4x) = 16x^2-12x+2\)
    • \(4f(x) = 4x^2-12x+8\)
    • \(f(-x) = x^2+3x+2\)
15. Para\(f(x) = \frac{x}{x-1}\)
    • \(f(3) = \frac{3}{2}\)
    • \(f(-1) = \frac{1}{2}\)
    • \(f\left(\frac{3}{2} \right) = 3\)
    • \(f(x-4) = \frac{x-4}{x-5}\)
    • \(f(x) - 4 = \frac{x}{x-1} - 4\)
    • \(\hphantom{f(x) - 4} = \frac{4-3x}{x-1}\)
    • \(f\left(x^2\right) = \frac{x^2}{x^2-1}\)
    • \(f(4x) = \frac{4x}{4x-1}\)
    • \(4f(x) = \frac{4x}{x-1}\)
    • \(f(-x) = \frac{x}{x+1}\)
16. Para\(f(x) = \frac{2}{x^3}\)
    • \(f(3) = \frac{2}{27}\)
    • \(f(-1) = -2\)
    • \(f\left(\frac{3}{2} \right) = \frac{16}{27}\)
    • \(f(x-4) = \frac{2}{(x-4)^3}\)
    • \(=\frac{2}{x^3-12x^2+48x-64}\)
    • \(f(x) - 4 = \frac{2}{x^3} - 4\)
    • \(\hphantom{f(x) - 4} = \frac{2-4x^3}{x^3}\)
    • \(f\left(x^2\right) = \frac{2}{x^6}\)
    • \(f(4x) = \frac{1}{32x^3}\)
    • \(4f(x) = \frac{8}{x^3}\)
    • \(f(-x) = -\frac{2}{x^3}\)
17. Para\(f(x) = 6\)
    • \(f(3) = 6\)
    • \(f(-1) =6\)
    • \(f\left(\frac{3}{2} \right) = 6\)
    • \(f(x-4) = 6\)
    • \(f(x) - 4 = 2\)
    • \(f\left(x^2\right) = 6\)
    • \(f(4x) = 6\)
    • \(4f(x) = 24\)
    • \(f(-x) = 6\)
18. Para\(f(x) = 0\)
    • \(f(3) = 0\)
    • \(f(-1) =0\)
    • \(f\left(\frac{3}{2} \right) = 0\)
    • \(f(x-4) = 0\)
    • \(f(x) - 4 = -4\)
    • \(f\left(x^2\right) = 0\)
    • \(f(4x) = 0\)
    • \(4f(x) = 0\)
    • \(f(-x) = 0\)
19. Para\(f(x) = 2x-5\)
    • \(f(2) = -1\)
    • \(f(-2) = -9\)
    • \(f(2a) = 4a-5\)
    • \(f \left( \frac{2}{a} \right) = \frac{4}{a} - 5\)
    • \(\hphantom{f \left( \frac{2}{a} \right)} = \frac{4-5a}{a}\)
    • \(\frac{f(a)}{2} =\frac{2a-5}{2}\)
    • \(f(a + h) = 2a + 2h - 5\)
    • \(2 f(a) = 4a-10\)
    • \(f(a+2) = 2a-1\)
    • \(f(a) + f(2) = 2a-6\)
20. Para\(f(x) = 5-2x\)
    • \(f(2) = 1\)
    • \(f(-2) = 9\)
    • \(f(2a) = 5-4a\)
    • \(f \left( \frac{2}{a} \right) = 5 - \frac{4}{a}\)
    • \(\hphantom{f \left( \frac{2}{a} \right)} = \frac{5a-4}{a}\)
    • \(\frac{f(a)}{2} = \frac{5-2a}{2}\)
    • \(f(a + h) = 5-2a-2h\)
    • \(2 f(a) = 10-4a\)
    • \(f(a+2) = 1-2a\)
    • \(f(a) + f(2) = 6-2a\)
21. Para\(f(x) = 2x^2-1\)
    • \(f(2) = 7\)
    • \(f(-2) = 7\)
    • \(f(2a) = 8a^2-1\)
    • \(f \left( \frac{2}{a} \right) = \frac{8}{a^2} - 1\)
    • \(\hphantom{f \left( \frac{2}{a} \right)} = \frac{8-a^2}{a^2}\)
    • \(\frac{f(a)}{2} = \frac{2a^2-1}{2}\)
    • \(f(a + h) = 2a^2+4ah+2h^2-1\)
    • \(2 f(a) = 4a^2-2\)
    • \(f(a+2) = 2a^2+8a+7\)
    • \(f(a) + f(2) = 2a^2+6\)
22. Para\(f(x) = 3x^2+3x-2\)
    • \(f(2) = 16\)
    • \(f(-2) = 4\)
    • \(f(2a) = 12a^2+6a-2\)
    • \(f \left( \frac{2}{a} \right) = \frac{12}{a^2} + \frac{6}{a} - 2\)
    • \(\hphantom{f \left( \frac{2}{a} \right)} = \frac{12+6a-2a^2}{a^2}\)
    • \(\frac{f(a)}{2} = \frac{3a^2+3a-2}{2}\)
    • \(f(a + h) = 3a^2 + 6ah + 3h^2+3a+3h-2\)
    • \(2 f(a) = 6a^2+6a-4\)
    • \(f(a+2) = 3a^2+15a+16\)
    • \(f(a) + f(2) = 3a^2+3a+14\)
23. Para\(f(x) = \sqrt{2x+1}\)
    • \(f(2) = \sqrt{5}\)
    • \(f(-2)\)no es real
    • \(f(2a) = \sqrt{4a+1}\)
    • \(f \left( \frac{2}{a} \right) = \sqrt{\frac{4}{a} + 1}\)
    • \(\hphantom{f \left( \frac{2}{a} \right)} = \sqrt{\frac{a+4}{a}}\)
    • \(\frac{f(a)}{2} = \frac{\sqrt{2a+1}}{2}\)
    • \(f(a + h) = \sqrt{2a+2h+1}\)
    • \(2 f(a) = 2\sqrt{2a+1}\)
    • \(f(a+2) = \sqrt{2a+5}\)
    • \(f(a) + f(2) =\sqrt{2a+1} + \sqrt{5}\)
24. Para\(f(x) = 117\)
    • \(f(2) = 117\)
    • \(f(-2) = 117\)
    • \(f(2a) = 117\)
    • \(f \left( \frac{2}{a} \right) = 117\)
    • \(\frac{f(a)}{2} = \frac{117}{2}\)
    • \(f(a + h) = 117\)
    • \(2 f(a) = 234\)
    • \(f(a+2) = 117\)
    • \(f(a) + f(2) = 234\)
25. Para\(f(x) = \frac{x}{2}\)
    • \(f(2) = 1\)
    • \(f(-2) = -1\)
    • \(f(2a) = a\)
    • \(f \left( \frac{2}{a} \right) = \frac{1}{a}\)
    • \(\frac{f(a)}{2} = \frac{a}{4}\)
    • \(f(a + h) = \frac{a+h}{2}\)
    • \(2 f(a) = a\)
    • \(f(a+2) = \frac{a+2}{2}\)

    • \(f(a) + f(2) = \frac{a}{2}+ 1\)
      \(\hphantom{f(a) + f(2)} = \frac{a+2}{2}\)

26. Para\(f(x) = \frac{2}{x}\)
    • \(f(2) = 1\)
    • \(f(-2) = -1\)
    • \(f(2a) = \frac{1}{a}\)
    • \(f \left( \frac{2}{a} \right) = a\)
    • \(\frac{f(a)}{2} = \frac{1}{a}\)
    • \(f(a + h) = \frac{2}{a+h}\)
    • \(2 f(a) = \frac{4}{a}\)
    • \(f(a+2) = \frac{2}{a+2}\)

    • \(f(a) + f(2) = \frac{2}{a}+1\)
      \(\hphantom{f(a)+f(2)}=\frac{a+2}{2}\)

27. Para\(f(x) = 2x-1\),\(f(0) = -1\) y\(f(x) = 0\) cuando\(x = \frac{1}{2}\)
28. Para\(f(x) = 3 - \frac{2}{5} x\),\(f(0) = 3\) y\(f(x) = 0\) cuando\(x = \frac{15}{2}\)
29. Para\(f(x) = 2x^2-6\),\(f(0) = -6\) y\(f(x) = 0\) cuando\(x = \pm \sqrt{3}\)
30. Para\(f(x) = x^2-x-12\),\(f(0) = -12\) y\(f(x) = 0\) cuando\(x = -3\) o\(x=4\)
31. Para\(f(x) = \sqrt{x+4}\),\(f(0) = 2\) y\(f(x) = 0\) cuando\(x =-4\)
32. Para\(f(x) = \sqrt{1-2x}\),\(f(0) = 1\) y\(f(x) = 0\) cuando\(x = \frac{1}{2}\)
33. Para\(\ f(x)=\frac{3}{4-x}, f(0)=\frac{3}{4}\) un\(\ f(x)\)) nunca es igual a 0
34. Para\(\ f(x)=\frac{3 x^{2}-12 x}{4-x^{2}}, f(0)=0\) un\(\ f(x)=0\) cuándo\(\ x = 0\) o\(\ x = 4\)
35. 1. \(\ f(-4)=1\)
    2. \(\ f(-3)=2\)
    3. \(\ f(3)=0\)
    4. \(\ f(3.001)=1.999\)
    5. \(\ f(-3.001)=1.999\)
    6. \(\ f(2)=\sqrt{5}\)
36. 1. \(\ f(4)=4\)
    2. \(\ f(-3)=9\)
    3. \(\ f(1)=0\)
    4. \(\ f(0)=1\)
    5. \(\ f(-1)=1\)
    6. \(\ f(-0.999) \approx 0.0447\)
37. \(\ (-\infty, \infty)\)
38. \(\ (-\infty, \infty)\)
39. \(\ (-\infty,-1) \cup(-1, \infty)\)
40. \(\ (-\infty,-2) \cup(-2,1) \cup(1, \infty)\)
41. \(\ (-\infty, \infty)\)
42. \(\ (-\infty,-\sqrt{3}) \cup(-\sqrt{3}, \sqrt{3}) \cup(\sqrt{3}, \infty)\)
43. \(\ (-\infty,-6) \cup(-6,6) \cup(6, \infty)\)
44. \(\ (-\infty, 2) \cup(2, \infty)\)
45. \(\ (-\infty, 3]\)
46. \(\ \left[-\frac{5}{2}, \infty\right)\)
47. \(\ [-3, \infty)\)
48. \(\ (-\infty, 7]\)
49. \(\ \left[\frac{1}{3}, \infty\right)\)
50. \(\ \left(\frac{1}{3}, \infty\right)\)
51. \(\ (-\infty, \infty)\)
52. \(\ \left[\frac{1}{3}, 3\right) \cup(3, \infty)\)
53. \(\ \left[\frac{1}{3}, 6\right) \cup(6, \infty)\)
54. \(\ (-\infty, \infty)\)
55. \(\ (-\infty, 8) \cup(8, \infty)\)
56. \(\ [0,8) \cup(8, \infty)\)
57. \(\ (8, \infty)\)
58. \(\ [7,9]\)
59. \(\ (-\infty, 8) \cup(8, \infty)\)
60. \(\ \left(-\infty,-\frac{1}{2}\right) \cup\left(-\frac{1}{2}, 0\right) \cup\left(0, \frac{1}{2}\right) \cup\left(\frac{1}{2}, \infty\right)\)
61. \(\ [0,5) \cup(5, \infty)\)
62. \(\ [0,25) \cup(25, \infty)\)
63. \(\ A(3)=9\), por lo que el área encerrada por un cuadrado con un lado de longitud 3 pulgadas es de 9 pulgadas cuadradas. Las soluciones a\(\ A(x) = 36\) son\(\ x=\pm 6\). Ya que\(\ x\) se restringe a\(\ x > 0\), sólo nos quedamos\(\ x = 6\). Esto significa que para que el área encerrada por el cuadrado sea de 36 pulgadas cuadradas, la longitud del lado debe ser de 6 pulgadas. Dado que\(\ x\) representa una longitud,\(\ x > 0\).
64. \(\ A(2)=4 \pi\), por lo que el área encerrada por un círculo con radio 2 es de metros\(\ 4 \pi\) cuadrados. La solución a\(\ A(r)=16 \pi\) ser\(\ r=\pm 4\). Ya que\(\ r\) se restringe a\(\ r > 0\), sólo nos quedamos\(\ r = 4\). Esto significa que para que el área encerrada por el círculo sea de metros\(\ 16 \pi\) cuadrados, el radio debe ser de 4 metros. Dado que\(\ r\) representa un radio (longitud),\(\ r>0\).
65. \(\ V(5)=125\), por lo que el volumen encerrado por un cubo con un lado de longitud 5 centímetros es de 125 centímetros cúbicos. La solución a\(\ V(x)=27\) es\(\ x = 3\). Esto significa que para que el volumen encerrado por el cubo sea de 27 centímetros cúbicos, la longitud del lado necesita de 3 centímetros. Dado que\(\ x\) representa una longitud,\(\ x>0\).
66. \(\ V(3)=36 \pi\), por lo que el volumen encerrado por una esfera con radio 3 es de pies\(\ 36 \pi\) cúbicos. La solución a\(\ V(r)=\frac{32 \pi}{3}\) es\(\ r=2\). Esto significa que para el volumen encerrado por la esfera pies\(\ \frac{32 \pi}{3}\) cúbicos, el radio necesita 2 pies. Dado que\(\ r\) representa un radio (longitud),\(\ r>0\).
67. \(\ h(0)=64\), por lo que en el momento en que el objeto se deja caer del edificio, el objeto se encuentra a 64 pies del suelo. La solución a\(\ h(t)=0\) son\(\ t=\pm 2\). Ya que restringimos\(\ 0 \leq t \leq 2\), sólo nos quedamos\(\ t = 2\). Esto significa que 2 segundos después de que el objeto es dejado caer del edificio, está a 0 pies del suelo. Dicho de otra manera, el objeto golpea el suelo después de 2 segundos. La restricción\(\ 0 \leq t \leq 2\) restringe el tiempo a estar entre el momento en que el objeto es liberado y el momento en que golpea el suelo.
68. \(\ T(0)=3\), por lo que a las 6 AM (0 horas después de las 6 AM), es\(\ 3^{\circ}\) Fahrenheit. \(\ T(6)=33\), por lo que al mediodía (6 horas después de las 6 AM), la temperatura es\(\ 33^{\circ}\) Fahrenheit. \(\ T(12)=27\), por lo que a las 6 PM (12 horas después de las 6 AM), es\(\ 27^{\circ}\) Fahrenheit.
69. \(\ C(0)=27\), por lo que para hacer 0 bolígrafos, cuesta ¹⁵ $2700. \(\ C(2)=11\), por lo que para hacer 2000 bolígrafos, cuesta 1100 dólares. \(\ C(5)=2\), por lo que para hacer 5000 bolígrafos, cuesta $2000.
70. \(\ F(0)=16.00\), por lo que en 1980 (0 años después de 1980), la economía promedio de combustible de los turismos en EU fue de 16.00 millas por galón. \(\ F(14)=20.81\), por lo que en 1994 (14 años después de 1980), la economía promedio de combustible de los turismos en EU fue de 20.81 millas por galón. \(\ F(28)=22.64\), por lo que en 2008 (28 años después de 1980), la economía promedio de combustible de los turismos en EU fue de 22.64 millas por galón.
71. \(\ P(0)=0\)lo que significa que en 1803 (0 años después de 1803), no hay Sasquatch en el condado de Portage. \(\ P(205)=\frac{3075}{22} \approx 139.77\), por lo que en 2008 (205 años después de 1803), hubo entre 139 y 140 Sasquatch en el condado de Portage.
72. 1. \(\ C(20)=300\). Cuesta $300 por 20 copias del libro.
    2. \(\ C(50)=675\), por lo que cuesta 675 dólares por 50 copias del libro. \(\ C(51)=612\), por lo que cuesta 612 dólares por 51 copias del libro.
    3. 56 libros.
73. 1. \(\ S(10)=17.5\), por lo que cuesta 17.50 dólares enviar 10 cómics.
    2. Hay envío gratuito en pedidos de 15 o más cómics.
74. 1. \(\ C(750) = 25\), por lo que cuesta 25 dólares platicar 750 minutos mensuales con este plan.
    2. Desde 20 horas = 1200 minutos, sustituimos\(\ m\) = 1200 y obtenemos\(\ C(1200) = 45\). Cuesta 45 dólares platicar 20 horas mensuales con este plan.
    3. Cuesta $25 por hasta 1000 minutos y 10 centavos por minuto por cada minuto más de 1000 minutos.
75. 1. \(\ \lfloor 0.785\rfloor=0,\lfloor 117\rfloor=117,\lfloor-2.001\rfloor=-3, \text { and }\lfloor\pi+6\rfloor=9\)

---

Referencia

¹ Consulte los Ejercicios para la Sección 1.1.

² o, 'dominio implícito'

³ La palabra 'implícita' es, pues, implícita.

⁴ El 'radicando' es la expresión 'dentro' del radical.

⁵ ¿Recuerdas por qué? Considera cuadrar ambos lados para 'resolver'\(\ \sqrt{t+1}=-2\).

⁶ Más precisamente, la fracción\(\ \frac{0}{0}\) es una 'forma indeterminante'. El cálculo se requiere domar a tales bestias.

⁷ Ver Secciones 2.5, 11.1 y 6.5, respectivamente.

⁸ En la humilde opinión de Carl, claro.

⁹ Podrías acercarte... dentro de un cierto margen de error especificado, quizás.

¹⁰ o, 'dominio explícito'

¹¹ ¿Quizás esto signifique devolver una libra de uvas?

¹² Lo que sube..

¹³ Ver el sitio web del Servicio de Impuestos Internos

¹⁴ El uso de la letra\(\ \mathbb{Z}\) para los enteros es ostensiblemente porque la palabra alemana zahlen significa 'contar'.

¹⁵ A esto se le llama el costo 'fijo' o 'start-up'. Volveremos a visitar este concepto en la página 82.