3.2: El teorema de los factores y el teorema del resto

Supongamos que deseamos encontrar los ceros de\(\ f(x)=x^{3}+4 x^{2}-5 x-14\). Establecer\(\ f(x) = 0\) resultados en la ecuación polinómica\(\ x^{3}+4 x^{2}-5 x-14=0\). A pesar de todas las técnicas de factorización que aprendimos ¹ en Álgebra Intermedia, esta ecuación nos ^{frustra 2} a cada paso. Si graficamos\(f\) usando la calculadora gráfica, obtenemos

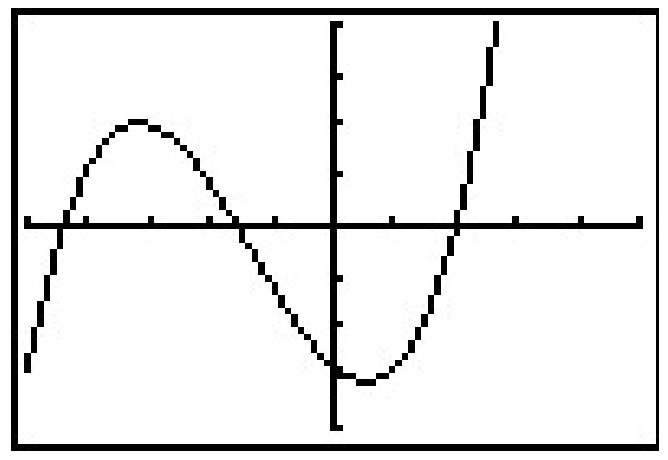
El gráfico sugiere que la función tiene tres ceros, uno de los cuales es\(\ x = 2\). Es fácil demostrarlo\(\ f(2) = 0\), pero los otros dos ceros parecen ser menos amigables. A pesar de que podríamos usar el comando 'Cero' para encontrar aproximaciones decimales para estos, buscamos un método para encontrar exactamente los ceros restantes. Con base en nuestra experiencia, si\(\ x = 2\) es un cero, parece que debería haber un factor de\(\ (x − 2)\) acecho en la factorización de\(\ f(x)\). En otras palabras, debemos esperar eso\(\ x^{3}+4 x^{2}-5 x-14=(x-2) q(x)\), donde\(\ q(x)\) está algún otro polinomio. ¿Cómo podríamos encontrar tal\(\ q(x)\), si siquiera existe? La respuesta viene de nuestro viejo amigo, la división polinómica. Dividiendo\(\ x^{3}+4 x^{2}-5 x-14\) por\(\ x − 2\) da

\ (\\\ begin {array} {r}
x^ {2} +6 x+\\\ 7\
x - 2\ longdiv {x ^ {3} + 4 x ^ {2} - 5 x - 1 4}
\\\\\ subrayado {- (x^3-2x^2)}\\\\\\\\\
\\\\\\\\\
\ subrayado {- (6x^2-12x)}\\\\\\\\\\\
7x-14\\\
\ subrayado {- (7x-14)}\\
0
\ end {array}\)

Como recordarán, esto significa\(\ x^{3}+4 x^{2}-5 x-14=(x-2)\left(x^{2}+6 x+7\right)\), así que para encontrar los ceros de\(\ f\), ahora resolvemos\(\ (x-2)\left(x^{2}+6 x+7\right)=0\). 0. Obtenemos\(\ x − 2 = 0\) (lo que nos da nuestro cero conocido,\(x = 2\)) así como\(\ x^{2}+6 x+7=0\). Este último no factorial muy bien, por lo que aplicamos la Fórmula Cuadrática para obtener\(\ x=-3 \pm \sqrt{2}\). El punto de esta sección es generalizar la técnica aplicada aquí. Primero, es un recordatorio amistoso de lo que podemos esperar cuando dividimos polinomios.

Teorema 3.4. División Polinomial

Supongamos\(\ d(x)\) y\(\ p(x)\) son polinomios distintos de cero donde el grado de\(\ p\) es mayor o igual al grado de\(\ d\). Existen dos polinomios únicos,\(\ q(x)\) y\(\ r(x)\), tal que\(\ p(x) = d(x) q(x) + r(x)\), donde cualquiera\(\ r(x) = 0\) o el grado de r es estrictamente menor que el grado de\(\ d\).

Como recordarás, todos los polinomios del Teorema 3.4 tienen nombres especiales. Al polinomio\(\ p\) se le llama dividendo;\(\ d\) es el divisor;\(\ q\) es el cociente;\(r\) es el resto. Si\(\ r(x) = 0\) entonces\(d\) se llama un factor de\(p\). La prueba del Teorema 3.4 suele ser relegada a un curso de Álgebra Abstracta, ³ pero aún podemos usar el resultado para establecer dos hechos importantes que son la base del resto del capítulo.

Teorema 3.5. El teorema del resto

Supongamos que\(\ p\) es un polinomio de grado al menos 1 y\(c\) es un número real. Cuando\(p(x)\) se divide por\(x − c\) el resto es\(p(c)\).

La prueba del Teorema 3.5 es una consecuencia directa del Teorema 3.4. Cuando un polinomio se divide por\(x − c\), el resto es 0 o tiene grado menor que el grado de\(x − c\). Ya que\(x − c\) es grado 1, el grado del resto debe ser 0, lo que significa que el resto es una constante. De ahí que en cualquier caso\(p(x) = (x − c) q(x) + r\),, donde\(r\), el resto, sea un número real, posiblemente 0. De ello se deduce\(p(c) = (c − c) q(c) + r = 0 · q(c) + r = r\), por lo que obtenemos\(r = p(c)\) según sea necesario. Hay una última 'fruta baja colgante' ⁴ para recolectar la cual presentamos a continuación.

Teorema 3.6. El teorema de los factores

Supongamos que\(p\) es un polinomio distinto de cero. El número real\(c\) es un cero de\(p\) si y sólo si\((x − c)\) es un factor de\(p(x)\).

La prueba de El teorema del factor es consecuencia de lo que ya conocemos. Si\((x − c)\) es un factor de\(p(x)\), esto significa\(p(x) = (x − c) q(x)\) para algún polinomio\(q\). De ahí\(p(c) = (c − c) q(c) = 0\),, entonces c es un cero de\(p\). Por el contrario, si\(c\) es un cero de\(p\), entonces\(p(c) = 0\). En este caso, El Teorema del Resto nos dice el resto cuando\(p(x)\) se divide por\((x − c)\), es decir\(p(c)\), es 0, lo que significa que\((x − c)\) es un factor de\(p\). Lo que hemos establecido es la conexión fundamental entre ceros de polinomios y factores de polinomios.

De las cosas que nos dice El Teorema del Factor, la más pragmática es que mejor teníamos que encontrar una manera más eficiente de dividir polinomios por cantidades de la forma\(x − c\). Afortunadamente, gente como Ruffini y Horner ya abrieron este rastro. Echemos un vistazo más de cerca a la división larga que realizamos al inicio de la sección e intentemos racionalizarla. En primer lugar, cambiemos todas las restaciones en adiciones distribuyéndolo a través de los −1s.

\ (\\\ begin {array} {r}
x^ {2} +6 x+7\\\\\
x-2\ longdiv {x^3+4x^2-5x-14}\
\\\\ subrayado {-x^3+2x^2}\\\\\\\\\\\\\\\\\\\\\\
6x^2-5x\\\\\\\\
\ underline línea {-6x^2+12x}\\\\\\\\\\
7x-14\\
\ subrayado {-7x+14}\\
0
\ end {array}\)

A continuación, observe que los términos\(\ -x^{3}\),\(\ -6 x^{2}\) y\(\ −7x\) son exactamente lo contrario de los términos por encima de ellos. El algoritmo que utilizamos asegura que este sea siempre el caso, por lo que podemos omitirlos sin perder ninguna información. También tenga en cuenta que los términos que 'derribar' (es decir, el\(\ −5x\) y\(−14\)) no son realmente necesarios para volver a copiar, así que los omitimos, también.

\ (\\\\ begin {array} {r}
x^ {2} +6 x+7\\\\\
x-2\ longdiv {x^3+4x^2-5x-14}
\\\\\\\ subrayado {\\\\\\\\\\ 2x^2}\\\\\\\\\\
\\\\\\\\\\\\\\\\\ subrayado {
\\\\\\\\\ 12x}\\\\\\\\\\ \\
7x\\\\\\\\\\\
\ subrayado {\\\\\\\\\ 14}\\\
0
\ end {array}\)

Ahora, vamos a subir un poco las cosas y, por razones que quedarán claras en un momento, copiemos el\(\ x^{3}\) en la última fila.

\ (\\\ begin {array} {r}
x^2+6x+7\\
x-2\ longdiv {x^3+4x^2-5x-14}
\\\\ subrayado {\\\\\\\\\\\\ 2x^2\\\ 12x\\\ 14}\\
x^3\\\\ 6x^2\\\\\ 7x\\\\\\ 0
\ end {array}\)

Obsérvese que al organizar las cosas de esta manera, cada término en la última fila se obtiene sumando los dos términos por encima de él. Observe también que el polinomio cociente se puede obtener dividiendo cada uno de los tres primeros términos de la última fila por\(\ x\) y sumando los resultados. Si te tomas el tiempo para trabajar de nuevo a través del problema de división original, encontrarás que esta es exactamente la forma en que determinamos el polinomio cociente. Esto significa que ya no necesitamos anotar el polinomio cociente, ni el\(\ x\) en el divisor, para determinar nuestra respuesta.

\ (\\ begin {array} {r}
-2\ mid x^ {3} &+4 x^ {2} &-5 x&-14\\
& 2 x^ {2} & 12 x & 14\
\ hline x^ {3} & 6 x^ {2} & 7 x & 0
\ end {array}\)

Hemos simplificado bastante las cosas hasta ahora, pero aún podemos hacer más. Tomemos un momento para recordarnos de dónde vino el\(\ 2 x^{2}\),\(\ 12x\) y 14 en la segunda fila. Cada uno de estos términos se obtuvo multiplicando los términos en el cociente,\(\ x^{2}\),\(\ 6x\) y 7, respectivamente, por −2 in\(x − 2\), luego por −1 cuando cambiamos la resta a suma. Multiplicar por −2 y luego por −1 es lo mismo que multiplicar por 2, así que reemplazamos −2 en el divisor por 2. Además, los coeficientes del polinomio cociente coinciden con los coeficientes de los tres primeros términos de la última fila, por lo que ahora damos el paso y escribimos solo los coeficientes de los términos para obtener

\ (\ begin {array} {r}
2\ mid1&4&5&14\\
&2&12&14\
\ hline
1&6&7&0
\ end {array}\)

Hemos construido un cuadro de división sintética para este problema de división polinómica. Reformulemos nuestro problema de división usando este cuadro para ver cómo agiliza enormemente el proceso de división. Para dividir\(\ x^{3}+4 x^{2}-5 x-14\) por\(x − 2\), escribimos 2 en el lugar del divisor y los coeficientes de\(x^{3}+4 x^{2}-5 x-14\) in para el dividendo. Después 'derribar' el primer coeficiente del dividendo.

\ (\\\ begin {array} {rrrrr}
2\ mid\ subrayado {\ 1\\ 4\\ -5\ -14}\ quad\ quad\ quad\ quad\ quad\ quad\ quad\ quad\ quad\ quad\ quad
2\ mid\\\ 1\\ 4
\ -5\\ -14\\\ flecha abajo\\\\\\\\\\\ overline {1
\\\\\\\\\\\\\\\\ \\\\\\\\\}
\ fin {matriz}\)

A continuación, toma el 2 del divisor y multiplica por el 1 que fue 'deraído' para obtener 2. Escribe esto debajo del 4, luego agrega para obtener 6.

\ (\\\ begin {array} {rl}
2\ mid\ &1\\ 4\ -5\ -14\ quad\ quad\ quad\ quad\ quad\ quad\ quad\ quad\ quad\ quad\ quad\ quad
2\ mid\ &1\\ 4\\
-5\\ -14\\ &\ downarrow
&\ downarrow\\ &\ overline {\\\\\\\\\\\\\\\\\\}
&\ overline {\\\\\\\\\\\\\\\\\\\\\\\\\\}\\\
&1 &1\\\ 6
\ end {array}\\)

Ahora toma el 2 del divisor por el 6 para obtener 12, y agrégalo al −5 para obtener 7.

\ (\\ begin {array} {rl}
2\ mid\ &1\\ 4\ -5\ -14\ quad\ quad\ quad\ quad\ quad\ quad\ quad\ quad\ quad\ quad\ quad\ quad\ quad
2\ mid\ &1\\ 4\\ -5\\ -14\\
&\ flecha abajo\ 2\\\ 12 &\ flecha abajo\ 2\\\
12\ línea {\\\\\\\\\\\\\\\\ \\\\\\\\\\}
&\ overline {\\\\\\\\\\\\\\\\\\\\\\\\\\\\}\\\\\\\\\\\\\\}\\
\\\\\\\\\\\\\}\\\\\\\\
\\}\\\\\\\

Por último, toma el 2 en el divisor por el 7 para obtener 14, y agrégalo al −14 para obtener 0.

\ (\ begin {array} {rl}
2\ mid\ &1\\ 4\ -5\ -14\ quad\ quad\ quad\ quad\ quad\ quad\ quad\ quad\ quad\ quad\ quad\ quad
2\ mid\ &1\\
4\ -5\\ -14\\ &\ flecha abajo\ 2\\\\ 12\\\\\ 12\\\\\\\ 14\\
&\ overline {\ \\\\\\\\\\\\\\\\\\\\\\\\\\}
&\ overline {\\\\\\\\\\\\\\\\\\\\\\\
\\\\\\\\\\\\\\\\\\\\\\\\\\\\ en caja {0}
\ end {array}\)

Los tres primeros números de la última fila de nuestro cuadro son los coeficientes del polinomio cociente. Recuerde, comenzamos con un polinomio de tercer grado y dividido por un polinomio de primer grado, por lo que el cociente es un polinomio de segundo grado. De ahí que el cociente sea\(x^{2}+6 x+7\). El número en la casilla es el resto. La división sintética es nuestra herramienta de elección para dividir polinomios por divisores de la forma\(x − c\). Es importante señalar que solo funciona para este tipo de divisores. ⁵ También toma nota que cuando un polinomio (de grado al menos 1) se divide por\(x − c\), el resultado será un polinomio de exactamente un grado menos. Por último, vale la pena el tiempo para rastrear cada paso en la división sintética de nuevo a su correspondiente paso en división larga. Si bien los autores han hecho todo lo posible para indicar de dónde viene el algoritmo, no hay sustituto para trabajar a través de él usted mismo.

Ejemplo 3.2.1

Utilice la división sintética para realizar las siguientes divisiones polinómicas. Encuentra el cociente y los polinomios restantes, luego escribe el dividendo, el cociente y el resto en la forma dada en el Teorema 3.4.

1. \(\left(5 x^{3}-2 x^{2}+1\right) \div(x-3)\)
2. \(\left(x^{3}+8\right) \div(x+2)\)
3. \(\frac{4-8 x-12 x^{2}}{2 x-3}\)

Solución

1. Al configurar el cuadro de división sintética, necesitamos ingresar 0 para el coeficiente de x en el dividendo. Hacerlo da

   \ (\\\ begin {array} {l}
   3\ mediados 5\\\ -2\\\\ 0\\\\\\\\\
   \ 1\\\\\\\\ flecha abajo\\\\\ 15\\\ 39\\ 117
   \\ overline {\\\\\\ 5\\\\\\ 13\\\ 39\\\ caja {118}}
   \ {matriz}\)

   Dado que el dividendo era un polinomio de tercer grado, el cociente es un polinomio cuadrático con coeficientes 5, 13 y 39. Nuestro cociente\(\ q(x)=5 x^{2}+13 x+39\) y el resto es\(r(x) = 118\). Según el Teorema 3.4, tenemos\(5 x^{3}-2 x^{2}+1=(x-3)\left(5 x^{2}+13 x+39\right)+118\).

2. Para esta división, reescribimos\(x + 2\) como\(x − (−2)\) y procedemos como antes

   \ (\\\ comenzar {array} {l}
   -2\ mediados 1\\\\\\\ 0\\\\\ 0\\\\\\\\ 8\\\
   \\\\\\\\\\ flecha abajo\\ -2\\\\ 4\\\ -8\\
   \ overline {\\\\\\\\\\\\ 1\\ -2\\\\\ 4\\\\\\ en caja {0}}
   \ end {array}\)

   Obtenemos el cociente\(\ q(x)=x^{2}-2 x+4\) y el resto\(r(x) = 0\). Relacionar el dividendo, cociente y resto da\(x^{3}+8=(x+2)\left(x^{2}-2 x+4\right)\).

3. Para\(\ 4-8 x-12 x^{2}\)\(2x − 3\) dividirlo, hay que hacer dos cosas. Primero, escribimos el dividendo en poderes descendentes de\(x\) as\(-12 x^{2}-8 x+4\). Segundo, ya que la división sintética funciona sólo para factores de la forma\(x − c\), nosotros factorizamos\(2x − 3\) como\(2\left(x-\frac{3}{2}\right)\). Nuestra estrategia es dividir primero\(-12 x^{2}-8 x+4\) por 2, para conseguir\(-6 x^{2}-4 x+2\). A continuación, dividimos por\(\left(x-\frac{3}{2}\right)\). El cuadro se convierte en

   \ (\ begin {array} {l}
   \ frac {3} {2}\ mediados -6\\\\\\\ -4\\\\\\\\\\\\\ 2
   \\\\\\\\\\\\ flecha abajo\\\\\ -9\\\\ -\ frac {39} {2}\\
   \\ overline {\\\\\ -6\\\\\\ -13\\\\\\ en caja {-\ frac {35} {2}}}
   \ end {array}\)

   De esto, obtenemos\(-6 x^{2}-4 x+2=\left(x-\frac{3}{2}\right)(-6 x-13)-\frac{35}{2}\). Multiplicando ambos lados por 2 y distribuyendo da\(-12 x^{2}-8 x+4=(2 x-3)(-6 x-13)-35\). En esta etapa, hemos escrito\(-12 x^{2}-8 x+4\) en la forma\((2x−3)q(x) +r(x)\), pero ¿cómo podemos estar seguros de que el polinomio cociente es\(−6x−13\) y el resto es −35? La respuesta es la palabra 'único' en el Teorema 3.4. El teorema afirma que solo hay una manera de descomponerse\(-12 x^{2}-8 x+4\) en un múltiplo de\((2x − 3)\) más un término constante. Ya que hemos encontrado tal manera, podemos estar seguros de que es la única manera.

El siguiente ejemplo reúne todos los conceptos discutidos en esta sección.

Ejemplo 3.2.2

Vamos\(p(x)=2 x^{3}-5 x+3\).

1. Encuentra\(p(−2)\) usando El Teorema del Resto. Consulta tu respuesta por sustitución.
2. Usa el hecho de que\(x = 1\) es un cero de factor\(p\) a\(p(x)\) y luego encuentra todos los ceros reales de\(p\).

Solución

1. El Teorema del Resto establece\(p(−2)\) es el resto cuando\(p(x)\) se divide por\(x − (−2)\). A continuación configuramos nuestro cuadro de división sintética. Tenemos cuidado de registrar el coeficiente de\(x^{2}\) como 0, y proceder como arriba

   \ (\ begin {array} {l}
   -2\ mediados\ 2\\\\\\\\ 0\\\\\\ -5\\\\\\\\\\\\ 3
   \\\\\\\\\\\\\\\\\\\\\\\ 3\\\\\\\\\
   \\\\\\\\\\\\\\\\\\\\\\\\\\\\\\ 3\\\\\\ en caja {-3}}
   \ final { matriz}\)

   Según el Teorema del Resto,\(p(−2) = −3\). Podemos verificar esto por sustitución directa en la fórmula para\(p(x)\):\(p(-2)=2(-2)^{3}-5(-2)+3=-16+10+3=-3\).

2. El Teorema del Factor nos dice que ya que\(x = 1\) es un cero de\(p\),\(x−1\) es un factor de\(p(x)\). Para factorizar\(p(x)\), dividimos

   \ (\ begin {array} {l}
   1\ mediados\ 2\\\\\ 0\\\\\\ -5\\\\\\\
   \\ 3\\\\\\\\\\ flecha abajo\\\\\ 2\\\\\\ 2\
   \\\\\\\\\\\\\\\\\\ -3\\\\\\\\\ en caja {0}}
   \ end {array}\)

   Obtenemos un resto de 0 lo que verifica eso, en efecto,\(p(1) = 0\). Nuestro polinomio cociente es un polinomio de segundo grado con coeficientes 2, 2 y −3. Entonces\(q(x)=2 x^{2}+2 x-3\). El teorema 3.4 nos dice\(p(x)=(x-1)\left(2 x^{2}+2 x-3\right)\). Para encontrar los ceros reales restantes de\(p\), tenemos que resolver\(2 x^{2}+2 x-3=0\) para\(x\). Como esto no factoriza muy bien, usamos la fórmula cuadrática para encontrar que los ceros restantes a\(x=\frac{-1 \pm \sqrt{7}}{2}\).

En la Sección 3.1, discutimos la noción de la multiplicidad de un cero. En términos generales, un cero con multiplicidad 2 se puede dividir dos veces en un polinomio; multiplicidad 3, tres veces y así sucesivamente. Esto se ilustra en el siguiente ejemplo.

Ejemplo 3.2.3

Vamos\(p(x)=4 x^{4}-4 x^{3}-11 x^{2}+12 x-3\). Dado que\(x=\frac{1}{2}\) es un cero de multiplicidad 2, encuentra todos los ceros reales de\(p\).

Solución

Preparamos para división sintética. Como se nos dice que la multiplicidad de\(\frac{1}{2}\) es dos, continuamos nuestro cuadro y\(\frac{1}{2}\) dividimos en el polinomio cociente

\ (\\\ begin {array} {r}
\ frac {1} {2}\ mediados de 4\\\\ -4\\\\\ -11\\\\\\\ 12\\\\\ -3\\
\\ subrayado {\\ flecha abajo\\\\\\\ 2\\\\\ -1\\\ -6\\\\\\\\\\\ 3}\
\ frac {1} {2}\ mediados 4\\\\ -2\\\\\ -12\\\\\\\\\\\ 6\\\\\\\\\\\\ en caja {0 }\\\
\\\\\\\\\\\\\\\\\\\\\\\\\\\ 0\\\\ -6\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\
\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\
\\\ end {array}\)

De la primera división, obtenemos\(4 x^{4}-4 x^{3}-11 x^{2}+12 x-3=\left(x-\frac{1}{2}\right)\left(4 x^{3}-2 x^{2}-12 x+6\right)\). La segunda división dice\(4 x^{3}-2 x^{2}-12 x+6=\left(x-\frac{1}{2}\right)\left(4 x^{2}-12\right)\). Combinando estos resultados, nosotros\(4 x^{4}-4 x^{3}-11 x^{2}+12 x-3=\left(x-\frac{1}{2}\right)^{2}\left(4 x^{2}-12\right)\). Para encontrar los ceros restantes de\(p\), establecemos\(4 x^{2}-12=0\) y obtenemos\(x=\pm \sqrt{3}\).

Vale la pena mencionar un par de cosas sobre el último ejemplo. Primero, la extensión del cuadro de división sintética para divisiones repetidas será un sitio común en las secciones por venir. Normalmente, comenzaremos con un polinomio de orden superior y despegaremos un cero a la vez hasta que nos quedemos con un cuadrático, cuyas raíces siempre se pueden encontrar usando la Fórmula Cuadrática. En segundo lugar, encontramos\(x=\pm \sqrt{3}\) son ceros de\(p\). El Teorema Factor garantiza\((x-\sqrt{3})\) y\((x-(-\sqrt{3}))\) son ambos factores de\(p\). Ciertamente podemos poner a prueba el Teorema de Factores y continuar el cuadro de división sintética desde arriba para ver qué sucede.

\ (\ begin {array} {r}
\ frac {1} {2}\ mediados de 4\\\\ -4\\\\\ -11\\\\\\\ 12\\\\\ -3\\
\\ subrayado {\\ flecha abajo\\\\\\\ 2\\\\\ -1\\\ -6\\\\\\\\\\\ 3}\
\ frac {1} {2}\ mediados 4\\\\ -2\\\\\ -12\\\\\\\\\\\ 6\\\\\\\\\\\\ en caja {0}\ \
\\\\\\\\\\\\\\\\\\\\\\\\\\ 0\\\\ -6\\\\\\\\\\\\\\\\\\\\
\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\
\\ subrayado {\ flecha abajo\\\\\ 4\ sqrt {3}\\\\\\\\ 12\\\\ \\\\\\\\\\\\\\\\\\\\\\\\\\\\\
\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\
\\\\\\\\\\\\\\\\ sqrt {3}\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\
\\\\\\ \\\\\\ en caja {0}\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\
\ end {array}\\)

Esto nos da\(4 x^{4}-4 x^{3}-11 x^{2}+12 x-3=\left(x-\frac{1}{2}\right)^{2}(x-\sqrt{3})(x-(-\sqrt{3}))(4)\), o, cuando se escribe con la constante al frente

\(\ p(x)=4\left(x-\frac{1}{2}\right)^{2}(x-\sqrt{3})(x-(-\sqrt{3}))\)

Hemos demostrado que\(p\) es producto de su coeficiente principal multiplicado por factores lineales de la forma\((x − c)\) donde\(c\) están los ceros de\(p\). Puede sorprender y deleitar al lector que, en teoría, todos los polinomios puedan reducirse a este tipo de factorización. Dejamos esa discusión a la Sección 3.4, porque los ceros pueden no ser números reales. Nuestro teorema final en la sección nos da un límite superior sobre el número de ceros reales.

Teorema 3.7

Supongamos que\(f\) es un polinomio de grado\(n \geq 1\). Entonces\(f\) tiene a lo sumo ceros\(n\) reales, contando multiplicidades.

El teorema 3.7 es una consecuencia del Teorema Factor y de la multiplicación polinómica. Cada cero\(c\) de f nos da un factor de la forma\((x − c)\) para\(f(x)\). Ya que\(f\) tiene grado\(n\), puede haber en la mayoría\(n\) de estos factores. La siguiente sección nos proporciona algunas herramientas que no sólo nos ayudan a determinar dónde se encuentran los ceros reales, sino cuáles números reales pueden ser.

Cerramos esta sección con un resumen de varios conceptos previamente presentados. Deberías tomarte el tiempo para mirar hacia atrás a través del texto para ver dónde se introdujo por primera vez cada concepto y dónde se hizo cada conexión con los otros conceptos.

Conexiones entre ceros, factores y gráficas de funciones polinómicas

Supongamos que\(p\) es una función polinómica de grado\(n \geq 1\). Las siguientes declaraciones son equivalentes:

• El número real\(c\) es un cero de\(p\)
• \(p(c) = 0\)
• \(x = c\)es una solución a la ecuación polinómica\(p(x) = 0\)
• \((x − c)\)es un factor de\(p(x)\)
• El punto\((c, 0)\) es una\(x\) -intercepción de la gráfica de\(y = p(x)\)

3.2.1 Ejercicios

En los Ejercicios 1 - 6, utilizar la división polinómica larga para realizar la división indicada. Escribe el polinomio en la forma\(p(x) = d(x)q(x) + r(x)\).

1. \(\left(4 x^{2}+3 x-1\right) \div(x-3)\)
2. \(\left(2 x^{3}-x+1\right) \div\left(x^{2}+x+1\right)\)
3. \(\left(5 x^{4}-3 x^{3}+2 x^{2}-1\right) \div\left(x^{2}+4\right)\)
4. \(\left(-x^{5}+7 x^{3}-x\right) \div\left(x^{3}-x^{2}+1\right)\)
5. \(\left(9 x^{3}+5\right) \div(2 x-3)\)
6. \(\left(4 x^{2}-x-23\right) \div\left(x^{2}-1\right)\)

En los Ejercicios 7 - 20 utilizan división sintética para realizar la división indicada. Escribe el polinomio en la forma\(p(x) = d(x)q(x)+r(x)\).

7. \(\left(3 x^{2}-2 x+1\right) \div(x-1)\)
8. \(\left(x^{2}-5\right) \div(x-5)\)
9. \(\left(3-4 x-2 x^{2}\right) \div(x+1)\)
10. \(\left(4 x^{2}-5 x+3\right) \div(x+3)\)
11. \(\left(x^{3}+8\right) \div(x+2)\)
12. \(\left(4 x^{3}+2 x-3\right) \div(x-3)\)
13. \(\left(18 x^{2}-15 x-25\right) \div\left(x-\frac{5}{3}\right)\)
14. \(\left(4 x^{2}-1\right) \div\left(x-\frac{1}{2}\right)\)
15. \(\left(2 x^{3}+x^{2}+2 x+1\right) \div\left(x+\frac{1}{2}\right)\)
16. \(\left(3 x^{3}-x+4\right) \div\left(x-\frac{2}{3}\right)\)
17. \(\left(2 x^{3}-3 x+1\right) \div\left(x-\frac{1}{2}\right)\)
18. \(\left(4 x^{4}-12 x^{3}+13 x^{2}-12 x+9\right) \div\left(x-\frac{3}{2}\right)\)
19. \(\left(x^{4}-6 x^{2}+9\right) \div(x-\sqrt{3})\)
20. \(\left(x^{6}-6 x^{4}+12 x^{2}-8\right) \div(x+\sqrt{2})\)

En los Ejercicios 21 - 30, determinar\(p(c)\) utilizando el Teorema del Resto para las funciones polinómicas dadas y el valor de\(c\). Si\(p(c)=0\), factor\(p(x)=(x-c) q(x)\).

21. \(p(x)=2 x^{2}-x+1, c=4\)
22. \(p(x)=4 x^{2}-33 x-180, c=12\)
23. \(p(x)=2 x^{3}-x+6, c=-3\)
24. \(p(x)=x^{3}+2 x^{2}+3 x+4, c=-1\)
25. \(p(x)=3 x^{3}-6 x^{2}+4 x-8, c=2\)
26. \(p(x)=8 x^{3}+12 x^{2}+6 x+1, c=-\frac{1}{2}\)
27. \(p(x)=x^{4}-2 x^{2}+4, c=\frac{3}{2}\)
28. \(p(x)=6 x^{4}-x^{2}+2, c=-\frac{2}{3}\)
29. \(p(x)=x^{4}+x^{3}-6 x^{2}-7 x-7, c=-\sqrt{7}\)
30. \(p(x)=x^{2}-4 x+1, c=2-\sqrt{3}\)

En los Ejercicios 31 - 40, se te da un polinomio y uno de sus ceros. Utilice las técnicas de esta sección para encontrar el resto de los ceros reales y factificar el polinomio.

31. \(x^{3}-6 x^{2}+11 x-6, \quad c=1\)
32. \(x^{3}-24 x^{2}+192 x-512, \quad c=8\)
33. \(3 x^{3}+4 x^{2}-x-2, \quad c=\frac{2}{3}\)
34. \(2 x^{3}-3 x^{2}-11 x+6, \quad c=\frac{1}{2}\)
35. \(x^{3}+2 x^{2}-3 x-6, \quad c=-2\)
36. \(2 x^{3}-x^{2}-10 x+5, \quad c=\frac{1}{2}\)
37. \(4 x^{4}-28 x^{3}+61 x^{2}-42 x+9, c=\frac{1}{2} \text { is a zero of multiplicity } 2\)
38. \(x^{5}+2 x^{4}-12 x^{3}-38 x^{2}-37 x-12, c=-1 \text { is a zero of multiplicity } 3\)
39. \(125 x^{5}-275 x^{4}-2265 x^{3}-3213 x^{2}-1728 x-324, c=-\frac{3}{5} \text { is a zero of multiplicity } 3\)
40. \(x^{2}-2 x-2, \quad c=1-\sqrt{3}\)

En los Ejercicios 41 - 45, crear un polinomio\(p\) que tenga las características deseadas. Se puede dejar el polinomio en forma factorizada.

41. • Los ceros de\(p\) son\(c=\pm 2\) y\(c=\pm 1\)
    • El término principal de\(p(x)\) es\(117 x^{4}\).
42. • Los ceros de\(p\) son\(c = 1\) y\(c = 3\)
    • \(c = 3\)es un cero de multiplicidad 2.
    • El término principal de\(p(x)\) es\(-5 x^{3}\)
43. • Las soluciones a\(p(x) = 0\) ser\(x=\pm 3\) y\(x = 6\)
    • El término principal de\(p(x)\) es\(7 x^{4}\)
    • El punto (−3, 0) es un mínimo local en la gráfica de\(y = p(x)\).
44. • Las soluciones a\(p(x) = 0\) son\(x=\pm 3\),\(x = −2\), y\(x = 4\).
    • El término principal de\(p(x)\) es\(-x^{5}\).
    • El punto (−2, 0) es un máximo local en la gráfica de\(y = p(x)\).
45. • \(p\)es grado 4.
    • como\(x \rightarrow \infty\),\(p(x) \rightarrow-\infty\)
    • \(p\)tiene exactamente tres\(x\) -intercepciones: (−6, 0), (1, 0) y (117, 0)
    • La gráfica de\(y = p(x)\) cruces a través del eje x en (1, 0).
46. Encuentra un polinomio cuadrático con coeficientes enteros que tenga\(x=\frac{3}{5} \pm \frac{\sqrt{29}}{5}\) como sus ceros reales.

3.2.2 Respuestas

1. \(4 x^{2}+3 x-1=(x-3)(4 x+15)+44\)
2. \(2 x^{3}-x+1=\left(x^{2}+x+1\right)(2 x-2)+(-x+3)\)
3. \(5 x^{4}-3 x^{3}+2 x^{2}-1=\left(x^{2}+4\right)\left(5 x^{2}-3 x-18\right)+(12 x+71)\)
4. \(-x^{5}+7 x^{3}-x=\left(x^{3}-x^{2}+1\right)\left(-x^{2}-x+6\right)+\left(7 x^{2}-6\right)\)
5. \(9 x^{3}+5=(2 x-3)\left(\frac{9}{2} x^{2}+\frac{27}{4} x+\frac{81}{8}\right)+\frac{283}{8}\)
6. \(4 x^{2}-x-23=\left(x^{2}-1\right)(4)+(-x-19)\)
7. \(\left(3 x^{2}-2 x+1\right)=(x-1)(3 x+1)+2\)
8. \(\left(x^{2}-5\right)=(x-5)(x+5)+20\)
9. \(\left(3-4 x-2 x^{2}\right)=(x+1)(-2 x-2)+5\)
10. \(\left(4 x^{2}-5 x+3\right)=(x+3)(4 x-17)+54\)
11. \(\left(x^{3}+8\right)=(x+2)\left(x^{2}-2 x+4\right)+0\)
12. \(\left(4 x^{3}+2 x-3\right)=(x-3)\left(4 x^{2}+12 x+38\right)+111\)
13. \(\left(18 x^{2}-15 x-25\right)=\left(x-\frac{5}{3}\right)(18 x+15)+0\)
14. \(\left(4 x^{2}-1\right)=\left(x-\frac{1}{2}\right)(4 x+2)+0\)
15. \(\left(2 x^{3}+x^{2}+2 x+1\right)=\left(x+\frac{1}{2}\right)\left(2 x^{2}+2\right)+0\)
16. \(\left(3 x^{3}-x+4\right)=\left(x-\frac{2}{3}\right)\left(3 x^{2}+2 x+\frac{1}{3}\right)+\frac{38}{9}\)
17. \(\left(2 x^{3}-3 x+1\right)=\left(x-\frac{1}{2}\right)\left(2 x^{2}+x-\frac{5}{2}\right)-\frac{1}{4}\)
18. \(\left(4 x^{4}-12 x^{3}+13 x^{2}-12 x+9\right)=\left(x-\frac{3}{2}\right)\left(4 x^{3}-6 x^{2}+4 x-6\right)+0\)
19. \(\left(x^{4}-6 x^{2}+9\right)=(x-\sqrt{3})\left(x^{3}+\sqrt{3} x^{2}-3 x-3 \sqrt{3}\right)+0\)
20. \(\left(x^{6}-6 x^{4}+12 x^{2}-8\right)=(x+\sqrt{2})\left(x^{5}-\sqrt{2} x^{4}-4 x^{3}+4 \sqrt{2} x^{2}+4 x-4 \sqrt{2}\right)+0\)
21. \(p(4)=29\)
22. \(p(12)=0, p(x)=(x-12)(4 x+15)\)
23. \(p(-3)=-45\)
24. \(p(-1)=2\)
25. \(p(2)=0, p(x)=(x-2)\left(3 x^{2}+4\right)\)
26. \(p\left(-\frac{1}{2}\right)=0, p(x)=\left(x+\frac{1}{2}\right)\left(8 x^{2}+8 x+2\right)\)
27. \(p\left(\frac{3}{2}\right)=\frac{73}{16}\)
28. \(p\left(-\frac{2}{3}\right)=\frac{74}{27}\)
29. \(p(-\sqrt{7})=0, p(x)=(x+\sqrt{7})\left(x^{3}+(1-\sqrt{7}) x^{2}+(1-\sqrt{7}) x-\sqrt{7}\right)\)
30. \(p(2-\sqrt{3})=0, p(x)=(x-(2-\sqrt{3}))(x-(2+\sqrt{3}))\)
31. \(x^{3}-6 x^{2}+11 x-6=(x-1)(x-2)(x-3)\)
32. \(x^{3}-24 x^{2}+192 x-512=(x-8)^{3}\)
33. \(3 x^{3}+4 x^{2}-x-2=3\left(x-\frac{2}{3}\right)(x+1)^{2}\)
34. \(2 x^{3}-3 x^{2}-11 x+6=2\left(x-\frac{1}{2}\right)(x+2)(x-3)\)
35. \(x^{3}+2 x^{2}-3 x-6=(x+2)(x+\sqrt{3})(x-\sqrt{3})\)
36. \(2 x^{3}-x^{2}-10 x+5=2\left(x-\frac{1}{2}\right)(x+\sqrt{5})(x-\sqrt{5})\)
37. \(4 x^{4}-28 x^{3}+61 x^{2}-42 x+9=4\left(x-\frac{1}{2}\right)^{2}(x-3)^{2}\)
38. \(x^{5}+2 x^{4}-12 x^{3}-38 x^{2}-37 x-12=(x+1)^{3}(x+3)(x-4)\)
39. \(125 x^{5}-275 x^{4}-2265 x^{3}-3213 x^{2}-1728 x-324=125\left(x+\frac{3}{5}\right)^{3}(x+2)(x-6)\)
40. \(x^{2}-2 x-2=(x-(1-\sqrt{3}))(x-(1+\sqrt{3}))\)
41. \(p(x)=117(x+2)(x-2)(x+1)(x-1)\)
42. \(p(x)=-5(x-1)(x-3)^{2}\)
43. \(p(x)=7(x+3)^{2}(x-3)(x-6)\)
44. \(p(x)=-(x+2)^{2}(x-3)(x+3)(x-4)\)
45. \(p(x)=a(x+6)^{2}(x-1)(x-117) \text { or } p(x)=a(x+6)(x-1)(x-117)^{2} \text { where } a \text { can be any negative real number}\)
46. \(p(x)=5 x^{2}-6 x-4\)

---

Referencia

¹ y probablemente se olvidó

² juego de palabras destinado

³ Sí, Virginia, hay cursos de Álgebra más abstractos que éste.

⁴ Jeff odia esta expresión y Carl la incluyó sólo para molestarlo.

⁵ Necesitarás usar buena división larga polinomial anticuada para divisores de grado mayores que 1.