3.1: Gráficas de polinomios

Tres de las familias de funciones estudiadas hasta ahora —constantes, lineales y cuadráticas— pertenecen a un grupo mucho mayor de funciones llamadas polinomios. Comenzamos nuestro estudio formal de polinomios generales con una definición y algunos ejemplos.

Definición 3.1: Función polinómica

Una función polinómica es una función de la forma

$\ f(x)=a_{n} x^{n}+a_{n-1} x^{n-1}+\ldots+a_{2} x^{2}+a_{1} x+a_{0},$

donde$a_0$,$a_{1}$,...,$a_{n}$ son números reales y$n \geq 1$ es un número natural. El dominio de una función polinómica es$(-\infty, \infty)$.

Hay varias cosas sobre la Definición 3.1 que pueden ser desfavorables o francamente aterradoras. Lo mejor que se puede hacer es mirar un ejemplo. Considerar$f(x) = 4x^5 - 3x^2 + 2x - 5$. ¿Es esta una función polinómica? Podemos reescribir la fórmula para$f$ como$f(x)= 4x^5 + 0 x^{4} + 0 x^{3} + (-3)x^2 + 2 x + (-5).$ Comparando esto con la Definición 3.1, identificamos$n=5$,$a_{5} = 4$,$a_{4} = 0$,$a_{3} = 0$,$a_{2} = -3$,$a_{1} = 2$ y$a_0 = -5$. En otras palabras,$a_{5}$ es el coeficiente de$x^{5}$,$a_{4}$ es el coeficiente de$x^{4}$, y así sucesivamente; el subíndice en los$a$'s simplemente indica a qué poder$x$ del coeficiente pertenece. El negocio de restringir$n$ a ser un número natural nos permite enfocarnos en animales algebraicos que se portan bien. ¹

Ejemplo 3.1.1

Determinar si las siguientes funciones son polinomios. Explica tu razonamiento.

1. $g(x) = \dfrac{4+x^3}{x}$
2. $p(x) = \dfrac{4x+x^3}{x}$
3. $q(x) = \dfrac{4x+x^3}{x^2+4}$
4. $f(x) =\sqrt[3]{x}$
5. $h(x) = |x|$
6. $z(x) = 0$

Solución.

1. Observamos directamente que el dominio de$g(x) = \frac{x^3+4}{x}$ es$x \neq 0$. Por definición, un polinomio tiene como dominio todos los números reales. De ahí que no$g$ pueda ser un polinomio.
2. A pesar de que$p(x) = \frac{x^3+4x}{x}$ simplifica a$p(x) = x^2+4$, que ciertamente se parece a la forma dada en la Definición 3.1$p$, el dominio de, que, como recordará, determinamos antes de simplificar, excluye$0$. Ay, no$p$ es una función polinómica por la misma razón$g$ no lo es.
3. Después de lo ocurrido con$p$ en la parte anterior, puede ser un poco tímido a la hora de simplificar$q(x) = \frac{x^3+4x}{x^2+4}$ a$q(x) = x$, lo que sin duda se ajusta a la Definición 3.1. Si miramos el dominio de$q$ antes simplificamos, vemos que es, efectivamente, todos los números reales. Una función que se puede escribir en forma de Definición 3.1 cuyo dominio son todos los números reales es, de hecho, un polinomio.
4. Podemos reescribir$f(x) =\sqrt[3]{x}$ como$f(x) = x^{\frac{1}{3}}$. Ya que no$\frac{1}{3}$ es un número natural, no$f$ es un polinomio.
5. La función$h(x) = |x|$ no es un polinomio, ya que no se puede escribir como una combinación de poderes de$x$ aunque se pueda escribir como una función por partes que involucra polinomios. Como veremos en esta sección, las gráficas de polinomios poseen una calidad ¹² que la gráfica de$h$ no posee.
6. No hay nada en la Definición 3.1 que impida que todos los coeficientes$a_{n}$, etc., sean$0$. De ahí$z(x) = 0$,, es un polinomio de honestidad a bondad.

Definición 3.2

Supongamos que$f$ es una función polinómica.

• Dado$f(x)=a_{n} x^{n}+a_{n-1} x^{n-1}+\ldots+a_{2} x^{2}+a_{1} x+a_{0} \text { with } a_{n} \neq 0$, decimos
  • El número natural$n$ se llama el grado del polinomio$f$.
  • El término$a_{n} x^{n}$ se denomina término principal del polinomio$f$.
  • Al número real$a_{n}$ se le llama el coeficiente principal del polinomio$f$.
  • Al número real$a_0$ se le llama término constante del polinomio$f$.
• Si$f(x) = a_0$, y$a_0 \neq 0$, decimos$f$ tiene grado$0$.
• Si$f(x) = 0$, decimos que no$f$ tiene título. ^a

---

^a Algunos autores dicen que$\ f(x) = 0$ tiene grado$\ -\infty$ por razones que ni siquiera vamos a entrar.

El lector bien puede preguntarse por qué hemos optado por separar las funciones constantes de los otros polinomios en la Definición 3.2. ¿Por qué no simplemente agruparlos a todos y, en lugar de obligarlos$n$ a ser un número natural$n = 1, 2, \ldots$,,$n$ permitir que sea un número entero,$n = 0, 1, 2, \ldots$. Podríamos unificar todos los casos, ya que, después de todo, ¿no$a_0x^{0} = a_0$? La respuesta es 'sí, siempre y cuando'$x\neq 0$. La función$f(x) = 3$ y$g(x) = 3x^{0}$ son diferentes, porque sus dominios son diferentes. El número$f(0) = 3$ está definido, mientras que no lo$g(0) = 3(0)^{0}$ es. ³ [formona indeterminada] De hecho, gran parte de la teoría que desarrollaremos en este capítulo no incluye las funciones constantes, por lo que bien podríamos tratarlas como forasteros desde el principio. Una cosa buena que viene de la Definición 3.2 es que ahora podemos pensar en las funciones lineales como funciones polinómicas de grado$1$ (o 'primer grado') y las funciones cuadráticas como funciones polinómicas de grado$2$ (o 'segundo grado').

Ejemplo 3.1.2

Encuentra el grado, término principal, coeficiente principal y término constante de las siguientes funciones polinómicas.

1. $f(x) = 4x^5 - 3x^2 + 2x - 5$
2. $g(x) = 12x +x^3$
3. $h(x) = \dfrac{4-x}{5}$
4. $p(x) = (2x-1)^{3}(x-2)(3x+2)$

Solución.

1. No hay sorpresas con$f(x) = 4x^5 - 3x^2 + 2x - 5$. Está escrito en la forma de Definición Definición 3.2, y vemos que el grado es$5$, el término principal es$4x^5$, el coeficiente principal es$4$ y el término constante es$-5$.
2. La forma dada en la Definición Definición 3.2 tiene el mayor poder de$x$ primero. Para ello, reescribimos$g(x) = 12x +x^3 = x^3+12x$, y vemos que el grado de$g$ es$3$, el término principal es$x^3$, el coeficiente principal es$1$ y el término constante es$0$.
3. Necesitamos reescribir la fórmula para$h$ que se asemeje a la forma dada en Definición Definición 3.2:$h(x) = \frac{4-x}{5} = \frac{4}{5} - \frac{x}{5} = -\frac{1}{5} x + \frac{4}{5}$. El grado de$h$ es$1$, el término principal es$-\frac{1}{5} x$, el coeficiente principal es$-\frac{1}{5}$ y el término constante es$\frac{4}{5}$.
4. Puede parecer que tenemos algún trabajo por delante para ponernos$p$ en forma de Definición Definición 3.2. Sin embargo, es posible obtener la información solicitada sobre$p$ sin multiplicar toda la expresión$(2x-1)^{3}(x-2)(3x+2)$. El término principal de$p$ será el término que tenga el mayor poder de$x$. La manera de obtener este término es multiplicar los términos con mayor potencia de$x$ de cada factor juntos - en otras palabras, el término principal de$p(x)$ es producto de los términos principales de los factores de$p(x)$. De ahí que el término principal de$p$ es$(2x)^3(x)(3x) = 24x^5$. Esto significa que el grado de$p$ es$5$ y el coeficiente principal es$24$. En cuanto al término constante, podemos realizar un truco similar. El término constante se obtiene multiplicando los términos constantes de cada uno de los factores$(-1)^3(-2)(2) = 4$.

Nuestro siguiente ejemplo muestra cómo los polinomios de mayor grado surgen 'naturalmente' ⁴ incluso en las aplicaciones geométricas más básicas.

Ejemplo 3.1.3

Una caja sin tapa se va a formar a partir de una pieza de cartón de una$10$$\times$$12$ pulgada recortando cuadrados congruentes de cada esquina del cartón y luego doblando las pestañas resultantes. Dejar$x$ denotar la longitud del lado del cuadrado que se retira de cada esquina.

1. Encuentra el volumen$V$ de la caja en función de$x$. Incluir un dominio aplicado apropiado.
2. Usa una calculadora gráfica para graficar$y=V(x)$ sobre el dominio que encontraste en la parte 1 y aproximar las dimensiones de la caja con volumen máximo a dos decimales. ¿Cuál es el volumen máximo?

Solución

1. Desde Geometría, eso lo sabemos$\mbox{Volume} = \mbox{width} \times \mbox{height} \times \mbox{depth}$. La clave es encontrar cada una de estas cantidades en términos de$x$. De la figura, vemos que la altura de la caja es$x$ en sí misma. La pieza de cartón es inicialmente$10$ pulgadas de ancho. Quitar cuadrados con una longitud lateral de$x$ pulgadas de cada esquina deja$10-2x$ pulgadas para el ancho. ⁵ En cuanto a la profundidad, el cartón es inicialmente$12$ pulgadas de largo, así que después de cortar$x$ pulgadas de cada lado, tendríamos$12-2x$ pulgadas restantes. Como función ⁶ de$x$, el volumen es$V(x) = x(10-2x)(12-2x) = 4x^3-44x^2+120x$ Para encontrar un dominio aplicado adecuado, observamos que para hacer una caja en todo lo que necesitamos$x > 0$. También la más corta de las dos dimensiones del cartón es$10$ pulgadas, y como estamos quitando$2x$ pulgadas de esta dimensión, también requerimos$10 - 2x > 0$ o$x < 5$. De ahí que nuestro dominio aplicado sea$0 < x < 5$.
2. Usando una calculadora gráfica, vemos que la gráfica de$y=V(x)$ tiene un máximo relativo. Porque$0 < x < 5$, este es también el máximo absoluto. Usando la función 'Máximo' de la calculadora, obtenemos$x \approx 1.81$,$y \approx 96.77$. Esto produce una altura de$x \approx 1.81$ pulgadas, un ancho de$10 - 2x \approx 6.38$ pulgadas y una profundidad de$12 - 2x \approx 8.38$ pulgadas. La$y$ coordenada -es el volumen máximo, que es aproximadamente pulgadas$96.77$ cúbicas (también escrito$\mbox{in}^3$).

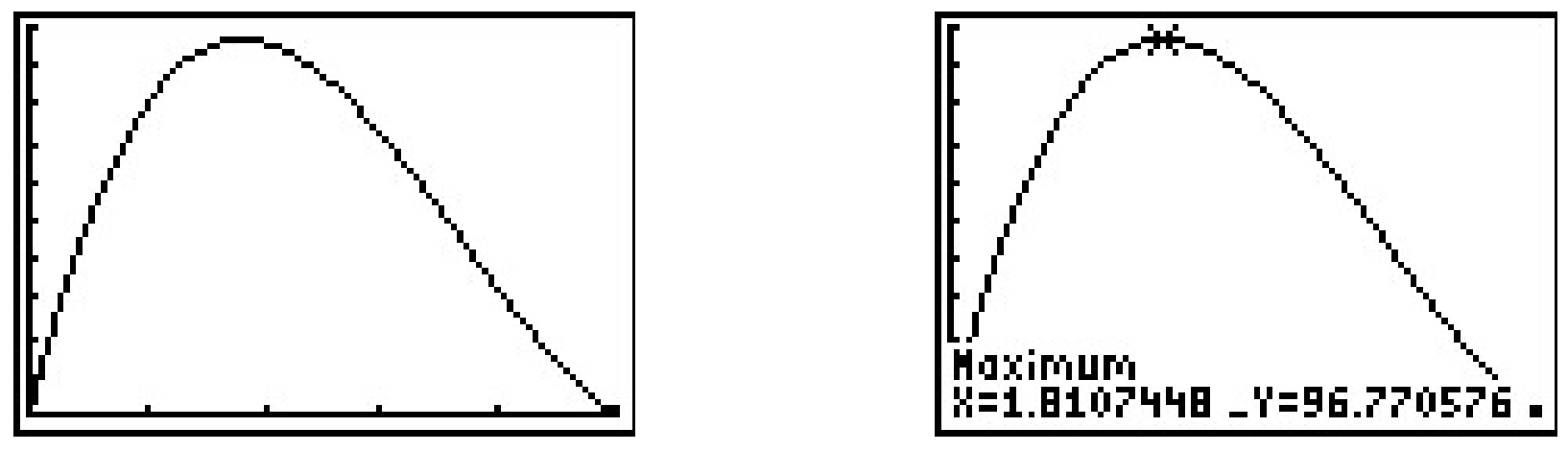
Para resolver el Ejemplo 3.1.3, hicimos buen uso de la gráfica del polinomio$y=V(x)$, por lo que debemos dirigir nuestra atención a las gráficas de polinomios en general. A continuación se muestran las gráficas de$y=x^2$,$y=x^4$ y$y=x^6$, lado a lado. Hemos omitido los ejes para permitirle ver que a medida que aumenta el exponente, el 'fondo' se vuelve 'más plano' y los 'lados' se vuelven 'más pronunciados'. Si te tomas el tiempo para graficar estas funciones a mano, ⁷ verás por qué.

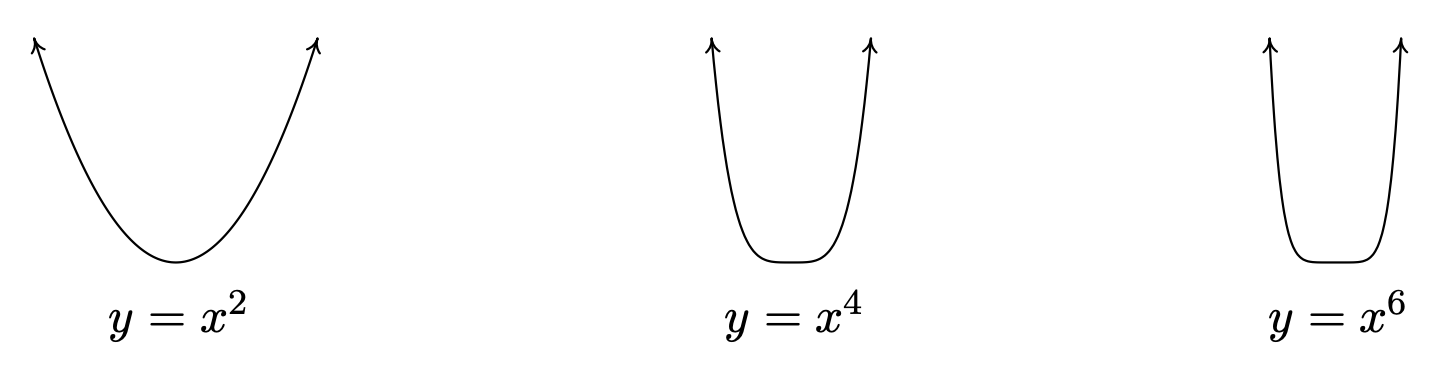
Todas estas funciones son parejos, (¿Recuerdas cómo mostrar esto?) y es exactamente porque el exponente es parejo. ⁸ Esta simetría es importante, pero queremos explorar una característica diferente pero igualmente importante de estas funciones que podemos ver gráficamente: su comportamiento final.

El comportamiento final de una función es una manera de describir lo que está sucediendo con los valores de la función (los$y$ -valores) a medida que los$x$ -valores se acercan a los 'extremos' del$x$ eje. ⁹ Es decir, lo que sucede a$y$ como$x$ se vuelve pequeño sin encuadernado ¹⁰ (escrito$x \rightarrow -\infty$) y, por otro lado, como$x$ se hace grande sin encuadernado ¹¹ (escrito$x \rightarrow \infty$).

Por ejemplo, dado$f(x) = x^2$, como$x \rightarrow -\infty$, nos imaginamos sustituyendo$x=-100$$x=-1000$,, etc., en$f$ para obtener$f(-100)=10000$$f(-1000)=1000000$, y así sucesivamente. Así, los valores de las funciones son cada vez más grandes números positivos (sin límite). Para describir este comportamiento, escribimos: as$x \rightarrow -\infty$,$f(x) \rightarrow \infty$. Si estudiamos el comportamiento de$f$ as$x \rightarrow \infty$, vemos que en este caso, también,$f(x) \rightarrow \infty$. (¡Te dijimos que la simetría era importante!) Lo mismo puede decirse de cualquier función de la forma$f(x) = x^n$ donde$n$ se encuentre un número parejo natural. Si generalizamos solo un poco para incluir escalamientos verticales y reflexiones a través del$x$ eje, ¹² tenemos

Comportamiento final de funciones$f(x) = ax^{n}$, $n$ even

Supongamos$f(x) = a x^{n}$ dónde$a \neq 0$ está un número real y$n$ es un número parejo natural. El comportamiento final de la gráfica$y=f(x)$ coincide con uno de los siguientes:

• para$a > 0$$x \rightarrow -\infty$, como$f(x) \rightarrow \infty$ y como$x \rightarrow \infty$,$f(x) \rightarrow \infty$
• para$a < 0$$x \rightarrow -\infty$, como$f(x) \rightarrow -\infty$ y como$x \rightarrow \infty$,$f(x) \rightarrow -\infty$

Gráficamente:

Ahora volvemos nuestra atención a funciones de la forma$f(x) = x^{n}$ donde$n \geq 3$ es un número natural impar. (Ignoramos el caso cuando$n=1$, ya que la gráfica de$f(x)=x$ es una línea y no se ajusta al patrón general de polinomios impares de grado superior.) A continuación hemos graficado$y=x^3$,$y=x^5$, y$y=x^7$. El 'aplanamiento' y 'empinado' que vimos con los poderes pares se presenta aquí también, y, no debería sorprendernos que todas estas funciones sean extrañas. ¹³ El comportamiento final de estas funciones es el mismo, con$f(x) \rightarrow -\infty$ como$x \rightarrow -\infty$ y$f(x) \rightarrow \infty$ como$x \rightarrow \infty$.

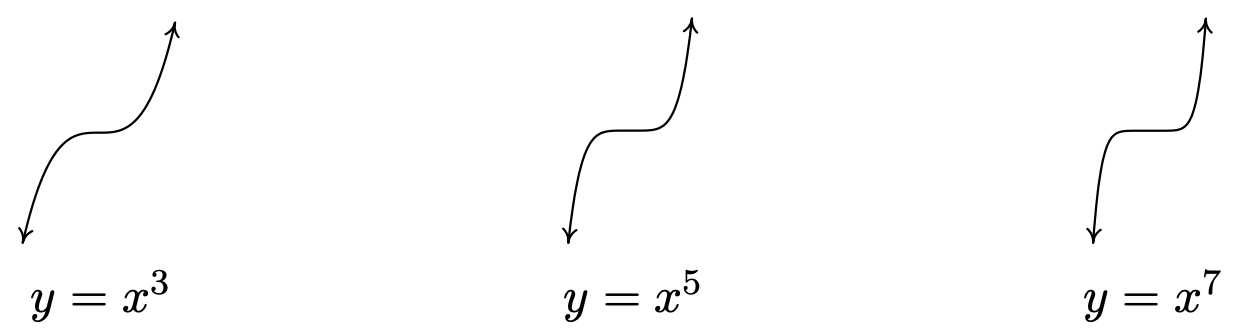
Al igual que con las funciones incluso graduadas que estudiamos anteriormente, podemos generalizar su comportamiento final.

Comportamiento final de funciones$f(x) = ax^{n}$, $n$ odd

Supongamos$f(x) = a x^{n}$ dónde$a \neq 0$ está un número real y$n \geq 3$ es un número natural impar. El comportamiento final de la gráfica$y=f(x)$ coincide con uno de los siguientes:

• para$a > 0$$x \rightarrow -\infty$, como$f(x) \rightarrow -\infty$ y como$x \rightarrow \infty$,$f(x) \rightarrow \infty$
• para$a < 0$$x \rightarrow -\infty$, como$f(x) \rightarrow \infty$ y como$x \rightarrow \infty$,$f(x) \rightarrow -\infty$

Gráficamente:

A pesar de tener un comportamiento final diferente, todas las funciones de la forma$f(x) = ax^{n}$ para números naturales$n$ comparten dos propiedades que ayudan a distinguirlos de otros animales en el zoológico de álgebra: son continuas y suaves. Si bien estos conceptos se definen formalmente usando Cálculo, ¹⁴ de manera informal, las gráficas de funciones continuas no tienen 'roturas' ni 'agujeros' en ellas, y las gráficas de funciones suaves no tienen 'giros bruscos'. Resulta que estos rasgos se conservan cuando se suman funciones, por lo que las funciones polinómicas generales heredan estas cualidades. A continuación encontramos la gráfica de una función que no es ni lisa ni continua, y a su derecha tenemos una gráfica de un polinomio, para su comparación. La función cuya gráfica aparece a la izquierda no logra ser continua donde tiene un 'break' o 'hole' en la gráfica; en todas partes, la función es continua. La función es continua en la 'esquina' y la 'cúspide', pero consideramos estos 'giros bruscos', por lo que estos son lugares donde la función no logra ser suave. Aparte de estos cuatro lugares, la función es suave y continua. Las funciones polinómicas son suaves y continuas en todas partes, como se muestra en la gráfica de la derecha.

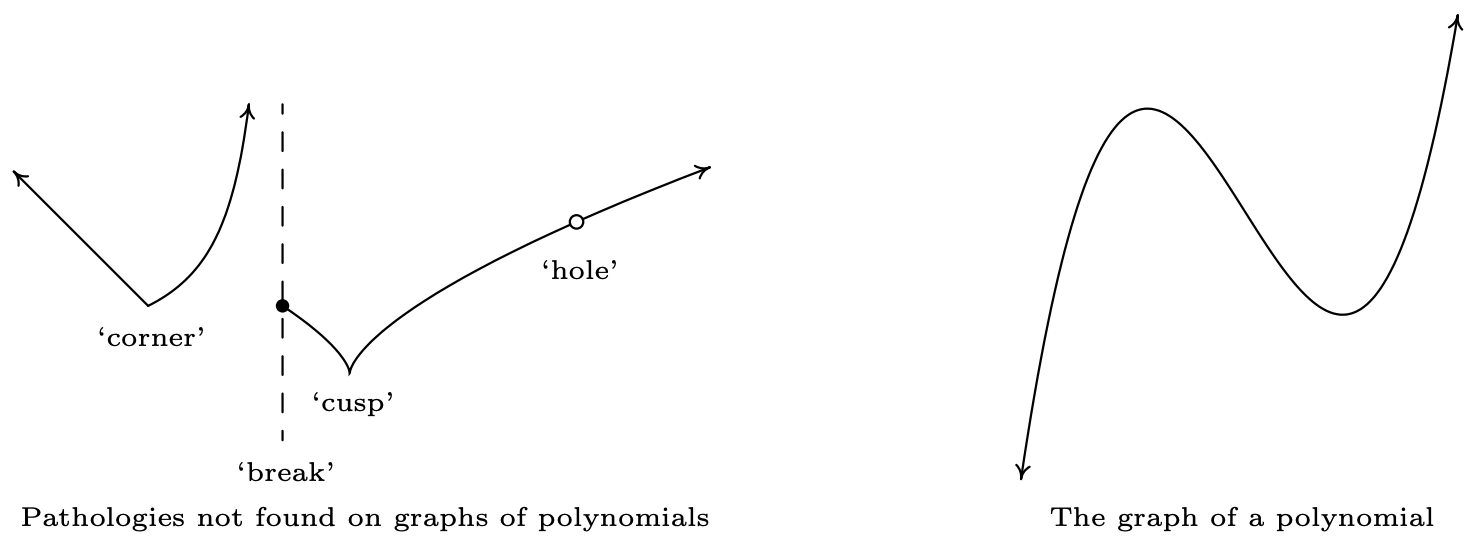
La noción de suavidad es lo que nos dice gráficamente que, por ejemplo,$f(x) = |x|$, cuya gráfica es la forma característica$\vee$ '', no puede ser un polinomio. La noción de continuidad es la que nos permitió construir el diagrama de signos para las desigualdades cuadráticas como lo hicimos en la Sección 2.4. Este último resultado se formaliza en el siguiente teorema.

Teorema 3.1. El Teorema del Valor Intermedio (Versión Cero)

Supongamos que$f$ es una función continua en un intervalo que contiene$x=a$ y$x=b$ con$a<b$. Si$f(a)$ y$f(b)$ tienen signos diferentes, entonces$f$ tiene al menos un cero entre$x = a$ y$x = b$; es decir, para al menos un número real$c$ tal que$a < c < b$, tenemos$f(c) = 0$.

El Teorema del Valor Intermedio es sumamente profundo; llega al corazón de lo que significa ser un número real, y es uno de los teoremas más utilizados y menos apreciados en Matemáticas. Dicho esto, la mayoría de los estudiantes ven el resultado como sentido común ya que dice, geométricamente, que la gráfica de una función polinómica no puede estar por encima del$x$ eje -en un punto y por debajo del$x$ eje en otro punto sin cruzar el$x$ -eje en algún punto intermedio. El siguiente ejemplo utiliza el Teorema del Valor Intermedio para establecer un hecho que la mayoría de los estudiantes dan por sentado. Muchos estudiantes, y tristemente algunos instructores, lo encontrarán tonto.

Ejemplo 3.1.4

Utilice el Teorema del Valor Intermedio para establecer que$\sqrt{2}$ es un número real.

Solución

Considerar la función polinómica$f(x) = x^2 - 2$. Entonces$f(1) = -1$ y$f(3) = 7$. Ya que$f(1)$ y$f(3)$ tienen diferentes signos, el Teorema del Valor Intermedio nos garantiza un número real$c$ entre$1$ y$3$ con$f(c) = 0$. Si$c^2 - 2 = 0$ entonces$c = \pm \sqrt{2}$. Ya que$c$ es entre$1$ y$3$,$c$ es positivo, entonces$c = \sqrt{2}$.

Nuestro uso principal del Teorema del Valor Intermedio está en la construcción de diagramas de signos, como en la Sección 2.4, ya que nos garantiza que las funciones polinómicas son siempre positivas$(+)$ o siempre negativas$(-)$ en intervalos que no contienen ninguno de sus ceros. El algoritmo general para polinomios se da a continuación.

Pasos para construir un diagrama de signos para una función polinómica

Supongamos que$f$ es una función polinómica.

1. Encuentra los ceros de$f$ y colócalos en la línea numérica con el número$0$ encima de ellos.
2. Elija un número real, denominado valor de prueba, en cada uno de los intervalos determinados en el paso 1.
3. Determine el signo de$f(x)$ para cada valor de prueba en el paso 2, y escriba ese signo por encima del intervalo correspondiente.

Ejemplo 3.1.5

Construya un diagrama de signos para$f(x) = x^3 (x-3)^2 (x+2) \left(x^2+1\right)$. Utilízala para dar un boceto aproximado de la gráfica de$y=f(x)$.

Solución

Primero, encontramos los ceros de$f$ resolviendo$x^3 (x-3)^2 (x+2)\left(x^2+1\right)=0$. Obtenemos$x=0$,$x=3$ y$x=-2$. (La ecuación no$x^2+1=0$ produce soluciones reales.) Estos tres puntos dividen la recta numérica real en cuatro intervalos:$(-\infty, -2)$,$(-2,0)$,$(0,3)$ y$(3,\infty)$. Seleccionamos los valores de prueba$x=-3$,$x=-1$,$x=1$ y$x=4$. Encontramos$f(-3)$ es$(+)$,$f(-1)$ es$(-)$ y$f(1)$ es$(+)$ tal como es$f(4)$. Donde quiera que$f$ esté$(+)$, su gráfica está por encima del$x$ eje -eje; donde quiera que$f$ esté$(-)$, su gráfica está debajo del$x$ eje -eje. Las$x$ -intercepciones de la gráfica de$f$ son$(-2,0)$,$(0,0)$ y$(3,0)$. Saber$f$ es suave y continuo nos permite esbozar su gráfica.

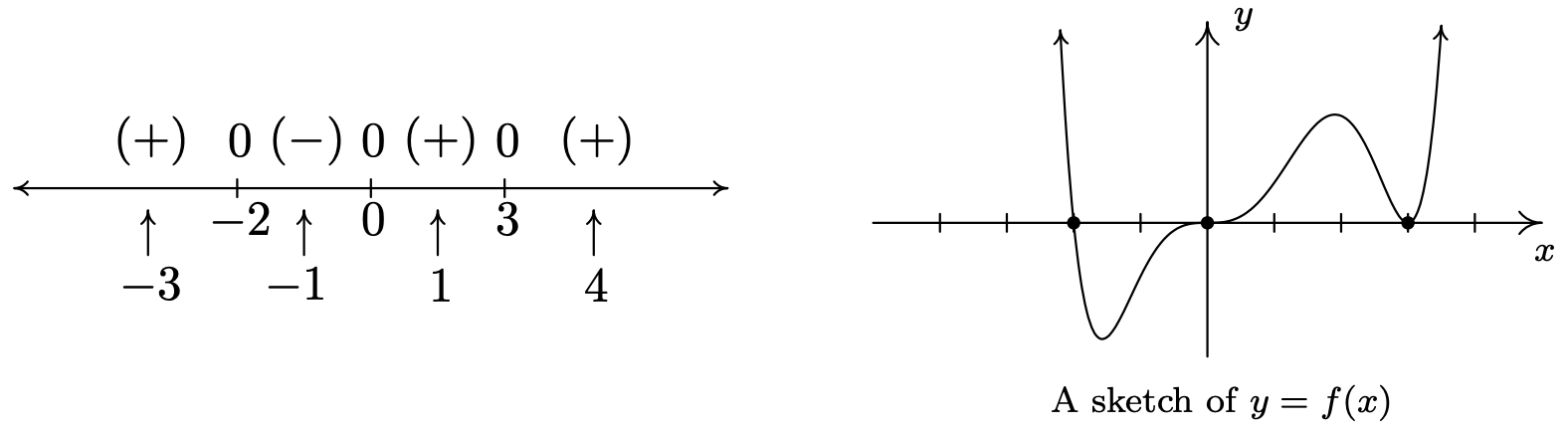
Un par de notas sobre el Ejemplo 3.1.5 están en orden. Primero, tenga en cuenta que a propósito no etiquetamos el$y$ eje -en el boceto de la gráfica de$y=f(x)$. Esto se debe a que el diagrama de signos nos da los ceros y la posición relativa de la gráfica; no nos da ninguna información sobre qué tan alto o bajo se desvía el gráfico del$x$ eje -eje. Además, como hemos mencionado anteriormente en el texto, sin Cálculo, los valores del máximo y mínimo relativos sólo se pueden encontrar aproximadamente usando una calculadora. Si nos tomáramos el tiempo para encontrar el término principal de$f$, encontraríamos que lo era$x^8$. Al observar el comportamiento final de$f$, notamos que coincide con el comportamiento final de$y=x^8$. Esto no es casualidad, como nos enteramos en el siguiente teorema.

Teorema 3.2. Comportamiento final para funciones polinomiales

El comportamiento final de un polinomio$f(x)=a_{n} x^{n}+a_{n-1} x^{n-1}+\ldots+a_{2} x^{2}+a_{1} x+a_{0} \text { with } a_{n} \neq 0$ coincide con el comportamiento final de$y = a_{n} x^{n}$.

Para ver por qué el Teorema 3.2 es cierto, primero veamos un ejemplo específico. Considerar$f(x) = 4x^3 - x + 5$. Si deseamos examinar el comportamiento final, buscamos ver el comportamiento de$f$ as$x \rightarrow \pm \infty$. Ya que estamos preocupados con$x$'s muy abajo del$x$ eje -, estamos lejos de$x=0$ así que podemos reescribir$f(x)$ para estos valores de$x$ como

$f(x) = 4x^3 \left( 1 - \dfrac{1}{4x^2} + \dfrac{5}{4x^3}\right)$

A medida que$x$ se vuelve sin límites (en cualquier dirección), los términos$\frac{1}{4x^2}$ y$\frac{5}{4x^3}$ se acercan cada vez más$0$, como indica la siguiente tabla.

$\begin{array}{|r||r|r|} \hline x & \frac{1}{4x^2} & \frac{5}{4x^3} \vphantom{\dfrac{a}{a}} \\[4pt] \hline -1000 & 0.00000025 & -0.00000000125 \\ \hline -100 & 0.000025 & -0.00000125 \\ \hline -10 & 0.0025 & -0.00125 \\ \hline 10 & 0.0025 & 0.00125 \\ \hline 100 & 0.000025 & 0.00000125 \\ \hline 1000 & 0.00000025 & 0.00000000125 \\ \hline \end{array}$

En otras palabras, as$x \rightarrow \pm \infty$,$f(x) \approx 4x^3\left( 1 - 0 +0\right) = 4x^3$, que es el término principal de$f$. La prueba formal del Teorema 3.2 funciona de la misma manera. Factorizar las hojas de término líder

$f(x) = a_{n} x^{n} \left( 1 + \dfrac{a_{n-\mbox{\tiny$1$}}}{a_{n} x}+ \ldots + \dfrac{a_2}{a_{n} x^{n-2}} + \dfrac{a_1}{a_{n} x^{n-1}}+\dfrac{a_0}{a_{n} x^{n}}\right)$

Como$x \rightarrow \pm \infty$, cualquier término con un$x$ en el denominador se vuelve cada vez más cerca$0$, y tenemos$f(x) \approx a_{n} x^{n}$. Geométricamente, el Teorema 3.2 dice que si graficamos$y=f(x)$ usando una calculadora gráfica, y seguimos 'alejando', la gráfica de la misma y su término principal se vuelven indistinguibles. A continuación se muestran las gráficas de$y=4x^3-x+5$ (la línea más gruesa) y$y=4x^3$ (la línea más delgada) en dos ventanas diferentes.

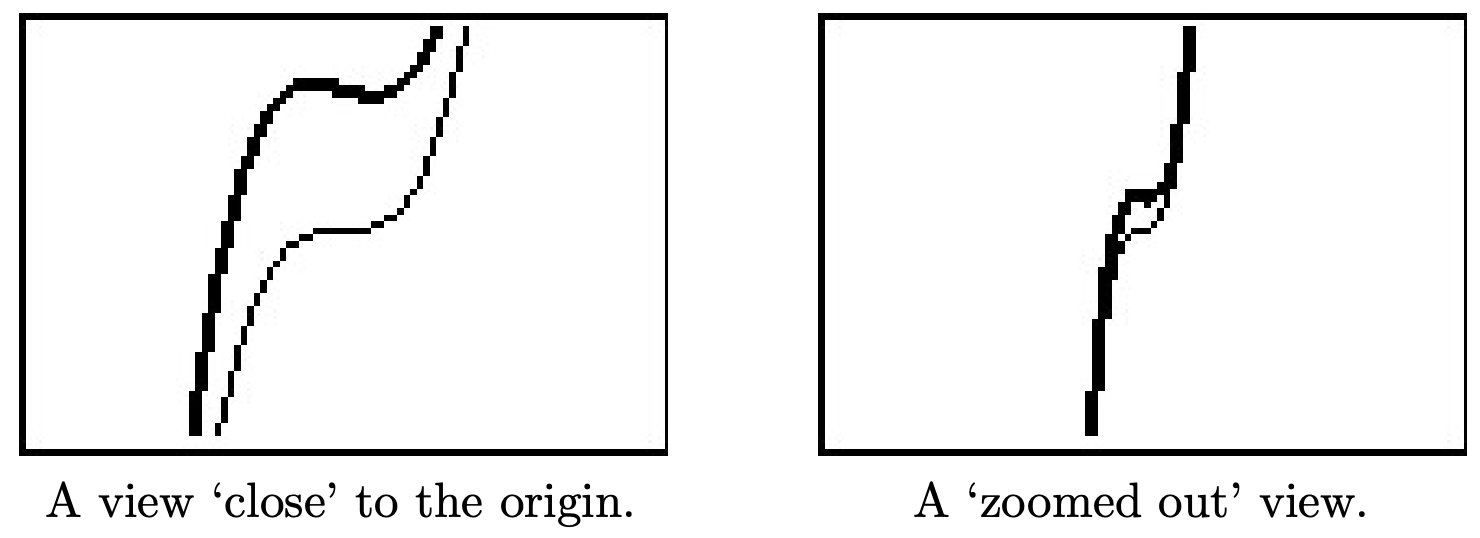
Volvamos a la función en el Ejemplo 3.1.5,$f(x) = x^3 (x-3)^2 (x+2)\left(x^2+1\right)$, cuyo diagrama de signos y gráfico se reproducen a continuación para referencia. El teorema 3.2 nos dice que el comportamiento final es el mismo que el de su término principal$x^{8}$. Esto nos dice que la gráfica de$y=f(x)$ arranca y termina por encima del$x$ eje -eje. En otras palabras,$f(x)$ es$(+)$ como$x \rightarrow \pm \infty$, y como resultado, ya no necesitamos evaluar$f$ en los valores de prueba$x=-3$ y$x=4$. ¿Hay alguna manera de eliminar la necesidad de evaluar$f$ en los otros valores de prueba? Lo que realmente necesitaríamos saber es cómo se comporta la función cerca de sus ceros - cruza a través del$x$ eje -en estos puntos, como lo hace en$x=-2$ y$x=0$, o simplemente toca y rebota como lo hace en$x=3$. Del diagrama de signos, la gráfica de$f$ cruzará el$x$ eje -siempre que los signos a ambos lados del cero cambien (como lo hacen en$x=-2$ y$x=0$); tocará cuando los signos sean los mismos a ambos lados del cero (como es el caso con$x=3$). Lo que necesitamos determinar es la razón detrás de si se produce o no el cambio de signo.

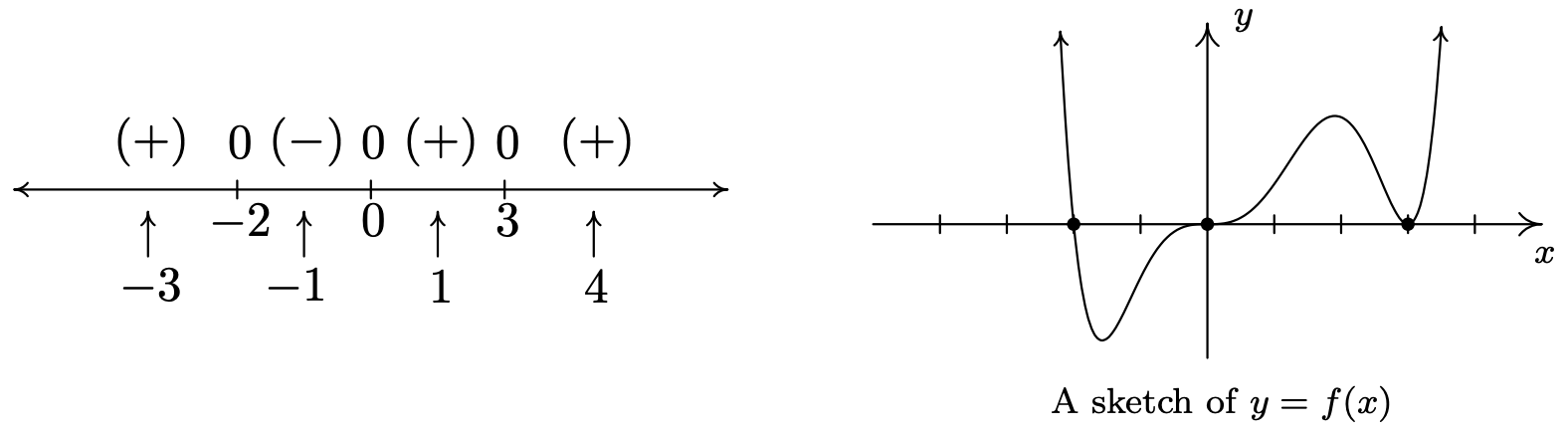
Afortunadamente, nos$f$ fue dado en forma factorizada:$f(x) = x^3 (x-3)^2 (x+2)$. Cuando intentamos determinar el signo de$f(-4)$, estamos intentando encontrar el signo del número$(-4)^3 (-7)^2 (-2)$, que resulta ser$(-)(+)(-)$ cuál es$(+)$. Si nos movemos al otro lado de$x=-2$, y encontramos el signo de$f(-1)$, estamos determinando el signo de$(-1)^3 (-4)^2 (+1)$, que es$(-)(+)(+)$ lo que nos da la$(-)$. Observe que los signos de los dos primeros factores en ambas expresiones son los mismos en$f(-4)$ y$f(-1)$. El único factor que cambia signo es el tercer factor,$(x+2)$, precisamente el factor que nos dio el cero$x=-2$. Si nos movemos al otro lado de$0$ y miramos de cerca$f(1)$, obtenemos el patrón de signo$(+1)^3(-2)^2(+3)$ o$(+)(+)(+)$ y notamos que, una vez más, pasando de$f(-1)$ a$f(1)$, el único factor que cambió de signo fue el primer factor$x^3$,, que corresponde al cero $x=0$. Por último, para encontrar$f(4)$, sustituimos para obtener$(+4)^3(+2)^2(+5)$ cuál es$(+)(+)(+)$ o$(+)$. El letrero no cambió por el factor medio$(x-3)^2$. A pesar de que este es el factor que corresponde al cero$x=3$, el hecho de que la cantidad sea cuadrada mantuvo el signo del factor medio igual a cada lado de$3$. Si miramos hacia atrás a los exponentes sobre los factores$(x+2)$ y$x^3$, vemos que ambos son impares, así como sustituimos valores a la izquierda y derecha de los ceros correspondientes, los signos de los factores correspondientes cambian lo que da como resultado que el signo del valor de la función cambie. Esta es la clave del comportamiento de la función cerca de los ceros. Necesitamos una definición y luego un teorema.

Definición 3.3.

Supongamos que$f$ es una función polinómica y$m$ es un número natural. Si$(x-c)^{m}$ es un factor de$f(x)$ pero no lo$(x-c)^{m+1}$ es, entonces decimos que$x=c$ es un cero de multiplicidad$m$.

De ahí, reescribir$f(x) = x^3 (x-3)^2 (x+2)$ como$f(x) = (x-0)^3 (x-3)^2 (x-(-2))^{1}$, vemos que$x=0$ es un cero de multiplicidad$3$,$x=3$ es un cero de multiplicidad$2$ y$x=-2$ es un cero de multiplicidad$1$.

Teorema 3.3. El papel de la multiplicidad

Supongamos que$f$ es una función polinómica y$x=c$ es un cero de multiplicidad$m$.

• Si$m$ es par, la gráfica de$y=f(x)$ toques y rebotes desde el$x$ eje -en$(c,0)$.
• Si$m$ es impar, la gráfica de$y=f(x)$ cruza a través del$x$ eje -en$(c,0)$.

Nuestro último ejemplo muestra cómo el comportamiento final y la multiplicidad nos permiten esbozar una gráfica decente sin apelar a un diagrama de signos.

Ejemplo 3.1.6

Esbozar la gráfica de$f(x) = -3(2x-1)(x+1)^2$ usar el comportamiento final y la multiplicidad de sus ceros.

Solución

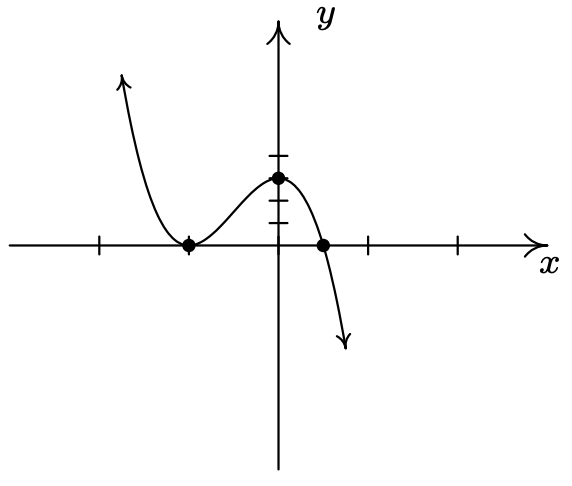
El comportamiento final de la gráfica de$f$ coincidirá con el de su término principal. Para encontrar el término principal, multiplicamos por los términos principales de cada factor para obtener$(-3)(2x)(x)^2 = -6x^3$. Esto nos dice que la gráfica comenzará por encima del$x$ eje -eje, en el Cuadrante II, y terminará por debajo del$x$ eje -eje, en el Cuadrante IV. A continuación, nos encontramos con los ceros de$f$. Afortunadamente para nosotros,$f$ se factoriza. ¹⁵ Establecer cada factor igual a cero da es$x = \frac{1}{2}$ y$x=-1$ como ceros. Para encontrar la multiplicidad de$x=\frac{1}{2}$ observamos que corresponde al factor$(2x-1)$. Esto no está estrictamente en la forma requerida en la Definición 3.3. Si factorizamos el$2$, sin embargo, obtenemos$(2x-1) = 2\left(x-\frac{1}{2}\right)$, y vemos que la multiplicidad de$x = \frac{1}{2}$ es$1$. Ya que$1$ es un número impar, sabemos por el Teorema 3.3 que la gráfica de$f$ cruzará a través del$x$ eje -en$\left(\frac{1}{2},0\right)$. Dado que el cero$x=-1$ corresponde al factor$(x+1)^2 = (x-(-1))^2$, encontramos que su multiplicidad es el$2$ que es un número par. Como tal, la gráfica de$f$ tocará y rebotará desde el$x$ eje -en$(-1,0)$. Aunque no se nos pide, podemos encontrar la$y$ -intercepción encontrando$f(0) = -3(2(0)-1)(0+1)^2 = 3$. Así$(0,3)$ es un punto adicional en la gráfica. Armando esto nos da la gráfica a continuación.

3.1.1 Ejercicios

En los Ejercicios 1 - 10, encuentra el grado, el término principal, el coeficiente principal, el término constante y el comportamiento final del polinomio dado.

1. $f(x) = 4-x-3x^2$
2. $g(x) = 3x^5 - 2x^2 + x + 1$
3. $q(r) = 1 - 16r^{4}$
4. $Z(b) = 42b - b^{3}$
5. $f(x) = \sqrt{3}x^{17} + 22.5x^{10} - \pi x^{7} + \frac{1}{3}$
6. $s(t) = -4.9t^{2} + v_0t + s_0$
7. $P(x) = (x - 1)(x - 2)(x - 3)(x - 4)$
8. $p(t) = -t^2(3 - 5t)(t^{2} + t + 4)$
9. $f(x) = -2x^3(x+1)(x+2)^2$
10. $G(t) = 4(t-2)^2\left(t+\frac{1}{2}\right)$

En los Ejercicios 11 - 20, encuentra los ceros reales del polinomio dado y sus correspondientes multiplicidades. Utilice esta información junto con un gráfico de signos para proporcionar un boceto aproximado de la gráfica del polinomio. Compara tu respuesta con el resultado de una utilidad gráfica.

11. $a(x) = x(x + 2)^{2}$
12. $g(x) = x(x + 2)^{3}$
13. $f(x) = -2(x-2)^2(x+1)$
14. $g(x) = (2x+1)^2(x-3)$
15. $F(x) = x^{3}(x + 2)^{2}$
16. $P(x) = (x - 1)(x - 2)(x - 3)(x - 4)$
17. $Q(x) = (x + 5)^{2}(x - 3)^{4}$
18. $h(x) = x^2(x-2)^2(x+2)^2$
19. $H(t) = (3-t)(t^2+1)$
20. $Z(b) = b(42 - b^{2})$

En los Ejercicios 21 - 26, dado el par de funciones$f$ y$g$, esbozar la gráfica$y=g(x)$ de comenzando con la gráfica de$y = f(x)$ y usando transformaciones. Rastrea al menos tres puntos de tu elección a través de las transformaciones. Indicar el dominio y el rango de$g$.

21. $f(x) = x^3$,$g(x) = (x + 2)^{3} + 1$
22. $f(x) = x^4$,$g(x) = (x + 2)^{4} + 1$
23. $f(x) = x^4$,$g(x) = 2 - 3(x - 1)^{4}$
24. $f(x) = x^5$,$g(x) = -x^{5} - 3$
25. $f(x) = x^5$,$g(x) = (x+1)^5+10$
26. $f(x) = x^6$,$g(x) = 8-x^6$
27. Utilice el Teorema del Valor Intermedio para demostrar que$f(x) = x^{3} - 9x + 5$ tiene un cero real en cada uno de los siguientes intervalos:$[-4, -3], [0, 1]$ y$[2, 3]$.
28. Ejemplo de retrabajo 3.1.3 asumiendo que la caja se va a hacer a partir de una hoja de papel de 8.5 pulgadas por 11 pulgadas. Usando tijeras y cinta adhesiva, construye la caja. ¿Te sorprende? ¹⁶

En los Ejercicios 29 - 31, supongamos que los ingresos$R$, en miles de dólares, por producir y vender$x$ cien televisores LCD se dan por$R(x) = -5x^3+35x^2+155x$ para$0 \leq x \leq 10.07$.

29. Utilice una utilidad gráfica para graficar$y = R(x)$ y determinar el número de televisores que deben venderse para maximizar los ingresos. ¿Cuál es el ingreso máximo? [lcdmaxprofitexerfirst]
30. Supongamos que el costo, en miles de dólares, para producir$x$ cien televisores LCD está dado por$C(x) = 200x + 25$ para$x \geq 0$. Encontrar y simplificar una expresión para la función de ganancia$P(x)$. (Recuerde: Beneficio = Ingresos - Costo.)
31. Utilice una utilidad gráfica para graficar$y = P(x)$ y determinar el número de televisores que deben venderse para maximizar las ganancias. ¿Cuál es el beneficio máximo? [lcdmaxprofitexerlast]
32. [newportaboycost] Mientras desarrollaba su nuevo juego, ¡Sasquatch Attack! , los creadores del PortaBoy (del Ejemplo 2.1.5) revisaron su función de costo y ahora usan$C(x) = .03x^{3} - 4.5x^{2} + 225x + 250$, para$x \geq 0$. Como antes,$C(x)$ es el costo de hacer$x$ PortaBoy Game Systems. La investigación de mercado indica que la función de demanda$p(x) = -1.5x + 250$ se mantiene sin cambios. Utilice una utilidad gráfica para encontrar el nivel de producción$x$ que maximice las ganancias obtenidas al producir y vender sistemas de juegos$x$ PortaBoy.
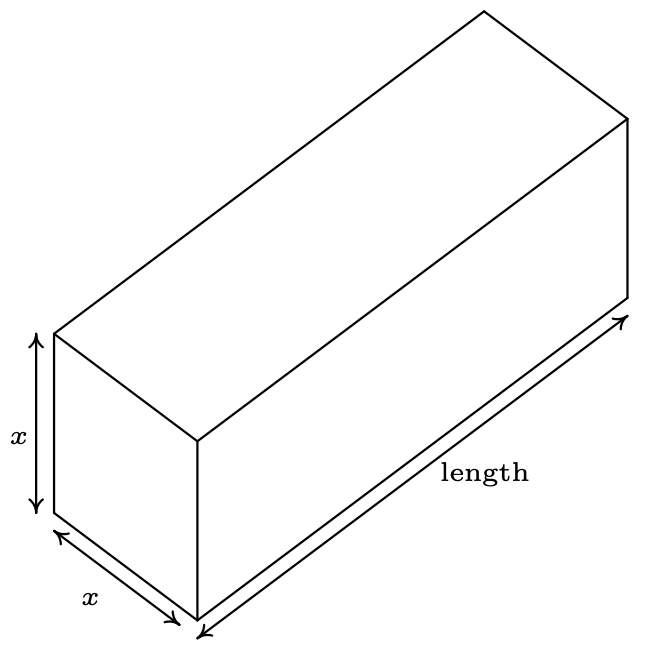
33. De acuerdo con la normativa Postal de Estados Unidos, una caja de envío rectangular debe satisfacer la desigualdad “Largo +$\leq$ Circunstancia 130 pulgadas” para el Puesto de Paquete y “Largo + Circundad$\leq$ 108 pulgadas” para otros servicios. Supongamos que tenemos una caja rectangular cerrada con una cara cuadrada de longitud lateral$x$ como se dibuja a continuación. La longitud es el lado más largo y está claramente etiquetado. El contorno es la distancia alrededor de la caja en las otras dos dimensiones por lo que en nuestro caso es la suma de los cuatro lados del cuadrado,$4x$.
    1. Suponiendo que vamos a estar por correo una caja a través de Parcel Post donde Longitud + Circunstancia$=$ 130 pulgadas, expresar la longitud de la caja en términos de$x$ y luego expresar el volumen$V$ de la caja en términos de$x$.
    2. Encuentra las dimensiones de la caja de volumen máximo que se puede enviar a través de Paquetería Postal.
    3. Repita las partes 33a y 33b si la caja se envía utilizando “otros servicios”.

       

34. Ahora revisamos el conjunto de datos del Ejercicio 6b en la Sección 2.5. En ese ejercicio, se le dio un gráfico del número de horas de luz que obtienen en el$21^{\mbox{st}}$ de cada mes en Fairbanks, Alaska basado en los datos de amanecer y atardecer de 2009 que se encuentran en el sitio web del Observatorio Naval de Estados Unidos. Dejamos$x = 1$ representar el 21 de enero de 2009,$x = 2$ representar el 21 de febrero de 2009, y así sucesivamente. El gráfico se da de nuevo como referencia.

    \ (\\ begin {array} {|l|r|r|r|r|r|r|r|r|r|r|r|r|r|}
    \ hline\ begin {array} {l}
    \ text {Mes}\
    \ texto {Número}
    \ end {array} & 1 y 2 y 3 y 4 y 5 y 6 y 7 y 8 y 9 y 10 y 11 y 12\\
    \ hline\ begin {array} {l}
    \ text {Horas de}\\
    \ text {Daylight}
    \ end {array} & 5.8 & 9.3 & 12.4 & 15.9 & 19.4 & 21.8 & 19.4 & 15.6 & 12.4 & 9.1 & 5.6 & 3.3\
    \ hline
    \ end {matriz}\)

    Encuentra polinomios cúbicos (tercer grado) y quárticos (cuarto grado) que modelan estos datos y comentan la bondad de ajuste para cada uno. ¿Qué podemos decir de usar cualquiera de los modelos para hacer predicciones sobre el año 2020? (Pista: Piense en el comportamiento final de los polinomios.) Usa los modelos para ver cuántas horas de luz tienen en tu cumpleaños y luego consulta el sitio web para ver qué tan precisos son los modelos. Sabiendo que los Sasquatch son en gran parte nocturnos, ¿qué días del año según tus modelos van a permitir al menos 14 horas de oscuridad para la investigación de campo sobre las esquivas criaturas?

35. Se construye un circuito eléctrico con una resistencia variable instalada. Para cada uno de los siguientes valores de resistencia (medidos en kilo-ohmios,$k \Omega$), la potencia correspondiente a la carga (medida en milivatios,$mW$) se da en la siguiente tabla. ¹⁷

    \ (\\ begin {array} {|l|l|l|l|l|l|l|l|}
    \ hline\ text {Resistencia:} (k\ Omega) & 1.012 & 2.199 & 3.275 & 4.676 & 6.805 & 9.975\
    \\ hline\ text {Potencia:} (m W) & 1.063 & 1.496 & 1.610 & 1.613 & 1.505 y 1.314\
    \ hline
    \ end {array}\)

    1. Haga un diagrama de dispersión de los datos usando la Resistencia como variable independiente y la Potencia como variable dependiente.
    2. Usa tu calculadora para encontrar modelos de regresión cuadrática (2do grado), cúbica (3º grado) y cuártica (4º grado) para los datos y juzgar la razonabilidad de cada uno.
    3. Para cada uno de los modelos encontrados anteriormente, encuentra la potencia máxima predicha que se puede entregar a la carga. ¿Cuál es el valor de resistencia correspondiente?
    4. Discuta con tus compañeros de clase las limitaciones de estos modelos, en particular, discute el comportamiento final de cada uno.
36. Mostrar que el comportamiento final de una función lineal$f(x) = mx + b$ es como debe ser de acuerdo a los resultados que hemos establecido en la sección para polinomios de grado impar. ²⁹ (Es decir, mostrar que la gráfica de una función lineal es “arriba en un lado y abajo en el otro” al igual que la gráfica de$y = a_{n}x^{n}$ para números impares$n$.)
37. Hay una sutileza sobre el papel de la multiplicidad que necesitamos discutir más a fondo; específicamente necesitamos ver 'cómo' la gráfica cruza el$x$ eje -en un cero de multiplicidad impar. En la sección, excluimos deliberadamente la función$f(x) = x$ de la discusión del comportamiento final de$f(x) = x^{n}$ para números impares$n$ y dijimos en su momento que se debía a que$f(x) = x$ no encajaba con el patrón que estábamos tratando de establecer. Acabas de demostrar en el ejercicio anterior que el comportamiento final de una función lineal se comporta como cualquier otro polinomio de grado impar, entonces, ¿qué no$f(x) = x$$g(x) = x^{3}$ hace eso? Es el 'aplanamiento' para valores$x$ cercanos a cero. Es este comportamiento local el que distinguirá entre un cero de multiplicidad 1 y uno de multiplicidad impar superior. Vuelva a mirar de cerca las gráficas de$a(x) = x(x + 2)^{2}$ y$F(x) = x^{3}(x + 2)^{2}$ del Ejercicio 3.1.1. Discuta con sus compañeros de clase cómo los gráficos son fundamentalmente diferentes en el origen. Podría ser útil usar una calculadora gráfica para acercar el origen y ver los diferentes comportamientos de cruce. También compare el comportamiento de$a(x) = x(x + 2)^{2}$ al de$g(x) = x(x + 2)^{3}$ cerca del punto$(-2, 0)$. ¿Qué predice que sucederá a los ceros de$f(x) = (x - 1)(x - 2)^2(x - 3)^{3}(x - 4)^{4}(x - 5)^{5}$?
38. Aquí hay algunas otras preguntas para que las discutas con tus compañeros de clase.
    1. ¿Cuántos extremos locales podría$n$ tener un polinomio de grado? ¿Cuán pocos extremos locales puede tener?
    2. ¿Podría un polinomio tener dos máximos locales pero no mínimos locales?
    3. Si un polinomio tiene dos máximos locales y dos mínimos locales, ¿puede ser de grado impar? ¿Puede ser de grado par?
    4. ¿Puede un polinomio tener extremos locales sin tener ceros reales?
    5. ¿Por qué cada polinomio de grado impar debe tener al menos un cero real?
    6. ¿Puede un polinomio tener dos ceros reales distintos y ningún extremo local?
    7. ¿Puede una$x$ intercepción producir un extremo local? ¿Puede producir un extremo absoluto?
    8. Si el$y$ -intercepto arroja un mínimo absoluto, ¿qué podemos decir del grado del polinomio y del signo del coeficiente principal?

3.1.2 Respuestas

1. $f(x) = 4-x-3x^2$
   Grado 2 Término
   $-3x^{2}$
   principal Coeficiente principal Término$-3$
   constante$4$
   As$x \rightarrow -\infty, \; f(x) \rightarrow -\infty$
   As$x \rightarrow \infty, \; f(x) \rightarrow -\infty$

2. $g(x) = 3x^5 - 2x^2 + x + 1$
   Grado 5 Término
   $3x^5$
   principal Coeficiente principal Término$3$
   constante$1$
   As$x \rightarrow -\infty, \; g(x) \rightarrow -\infty$
   As$x \rightarrow \infty, \; g(x) \rightarrow \infty$

3. $q(r) = 1 - 16r^{4}$
   Grado 4 Término
   $-16r^{4}$
   principal Coeficiente principal Término$-16$
   constante$1$
   As$r \rightarrow -\infty, \; q(r) \rightarrow -\infty$
   As$r \rightarrow \infty, \; q(r) \rightarrow -\infty$

4. $Z(b) = 42b - b^{3}$
   Grado 3 Término
   $-b^{3}$
   principal Coeficiente principal Término$-1$
   constante$0$
   As$b \rightarrow -\infty, \; Z(b) \rightarrow \infty$
   As$b \rightarrow \infty, \; Z(b) \rightarrow -\infty$

5. $f(x) = \sqrt{3}x^{17} + 22.5x^{10} - \pi x^{7} + \frac{1}{3}$
   Grado 17 Término
   $\sqrt{3}x^{17}$
   principal Coeficiente principal Término$\sqrt{3}$
   constante$\frac{1}{3}$
   As$x \rightarrow -\infty, \; f(x) \rightarrow -\infty$
   As$x \rightarrow \infty, \; f(x) \rightarrow \infty$

6. $s(t) = -4.9t^{2} + v_0t + s_0$
   Grado 2 Término
   $-4.9t^{2}$
   principal Coeficiente principal Término$-4.9$
   constante$s_0$
   As$t \rightarrow -\infty, \; s(t) \rightarrow -\infty$
   As$t \rightarrow \infty, \; s(t) \rightarrow -\infty$

7. $P(x) = (x - 1)(x - 2)(x - 3)(x - 4)$
   Grado 4 Término
   $x^{4}$
   principal Coeficiente principal Término$1$
   constante$24$
   As$x \rightarrow -\infty, \; P(x) \rightarrow \infty$
   As$x \rightarrow \infty, \; P(x) \rightarrow \infty$

8. $p(t) = -t^2(3 - 5t)(t^{2} + t + 4)$
   Grado 5 Término
   $5t^{5}$
   principal Coeficiente principal Término$5$
   constante$0$
   As$t \rightarrow -\infty, \; p(t) \rightarrow -\infty$
   As$t \rightarrow \infty, \; p(t) \rightarrow \infty$

9. $f(x) = -2x^3(x+1)(x+2)^2$
   Grado 6 Término
   $-2x^{6}$
   principal Coeficiente principal Término$-2$
   constante$0$
   As$x \rightarrow -\infty, \; f(x) \rightarrow -\infty$
   As$x \rightarrow \infty, \; f(x) \rightarrow -\infty$

10. $G(t) = 4(t-2)^2\left(t+\frac{1}{2}\right)$
    Grado 3 Término
    $4t^3$
    principal Coeficiente principal Término$4$
    constante$8$
    As$t \rightarrow -\infty, \; G(t) \rightarrow -\infty$
    As$t \rightarrow \infty, \; G(t) \rightarrow \infty$

11. $a(x) = x(x + 2)^{2}$
    $x = 0$multiplicidad 1
    $x = -2$ multiplicidad 2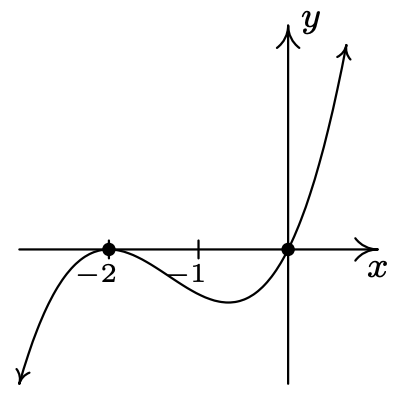

    

12. $g(x) = x(x + 2)^{3}$
    $x = 0$multiplicidad 1
    $x = -2$ multiplicidad 3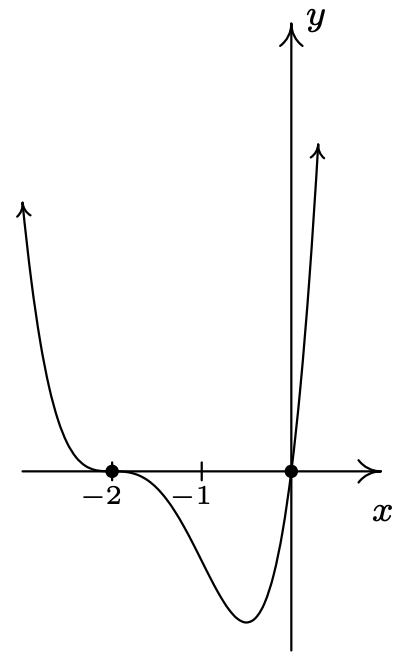

    

13. $f(x) = -2(x-2)^2(x+1)$
    $x=2$multiplicidad 2
    $x=-1$ multiplicidad 1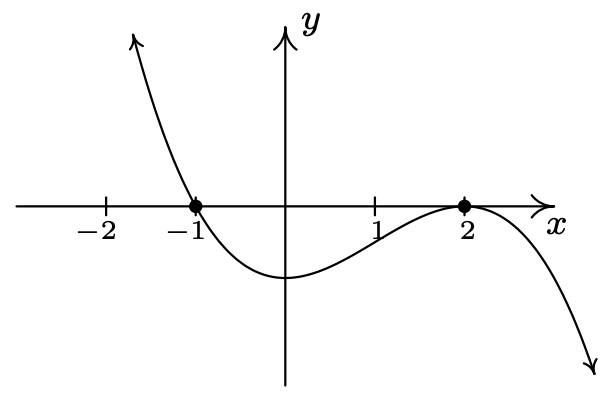

    

14. $g(x) = (2x+1)^2(x-3)$
    $x=-\frac{1}{2}$multiplicidad 2
    $x=3$ multiplicidad 1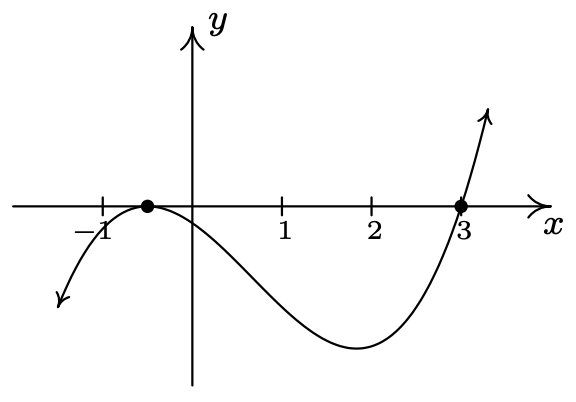

    

15. $F(x) = x^{3}(x + 2)^{2}$
    $x = 0$multiplicidad 3
    $x = -2$ multiplicidad 2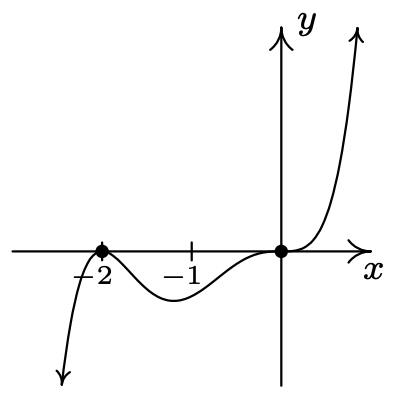

    

16. $P(x) = (x - 1)(x - 2)(x - 3)(x - 4)$
    $x = 1$multiplicidad 1
    $x = 2$ multiplicidad 1
    $x = 3$ multiplicidad 1
    $x = 4$ multiplicidad 1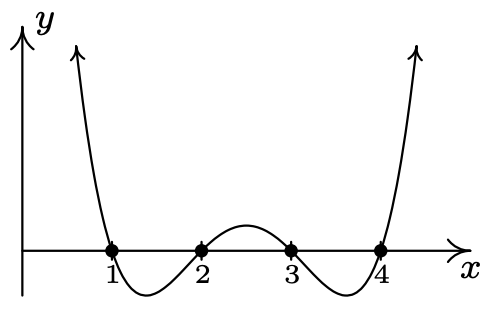

    

17. $Q(x) = (x + 5)^{2}(x - 3)^{4}$
    $x = -5$multiplicidad 2
    $x = 3$ multiplicidad 4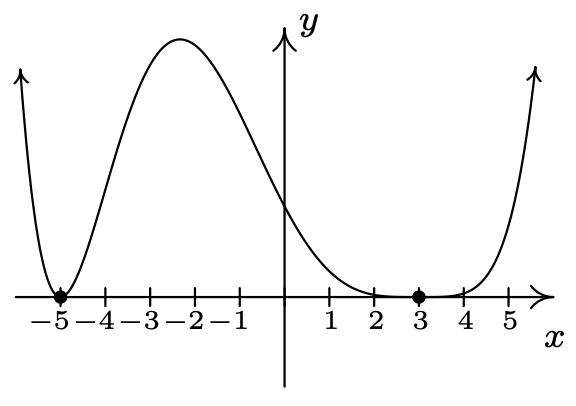

    

18. $f(x) = x^2(x-2)^2(x+2)^2$
    $x = -2$multiplicidad 2
    $x = 0$ multiplicidad 2
    $x = 2$ multiplicidad 2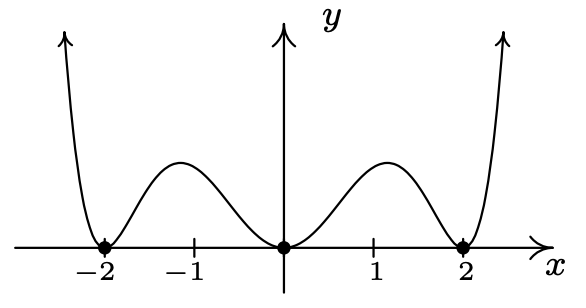

    

19. $H(t) = (3-t)\left(t^2+1\right)$
    $x =3$multiplicidad 1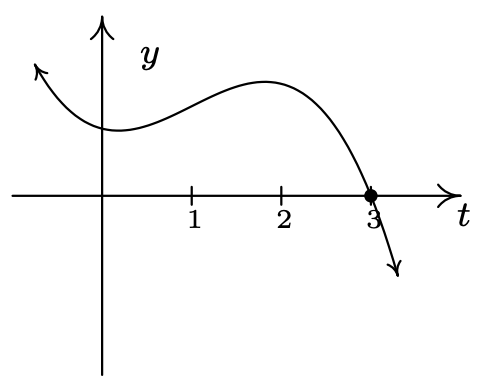

    

20. $Z(b) = b(42 - b^{2})$
    $b = -\sqrt{42}$multiplicidad 1
    $b = 0$ multiplicidad 1
    $b = \sqrt{42}$ multiplicidad 1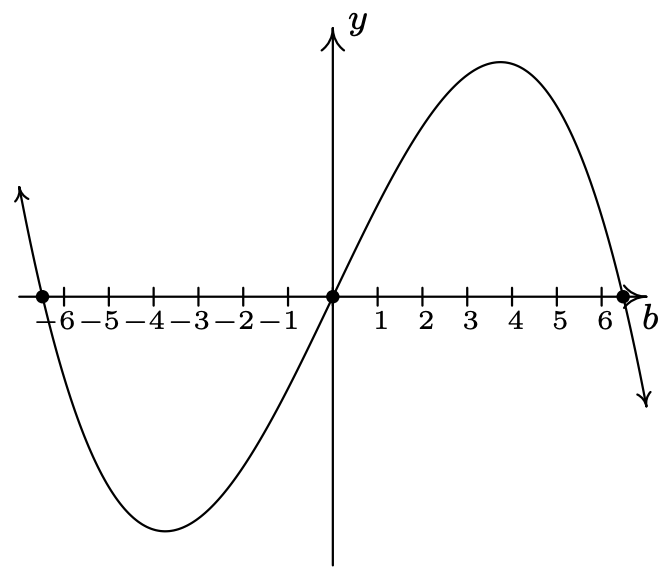

    

21. $g(x) = (x + 2)^{3} + 1$
    dominio:$(-\infty, \infty)$
    rango:$(-\infty, \infty)$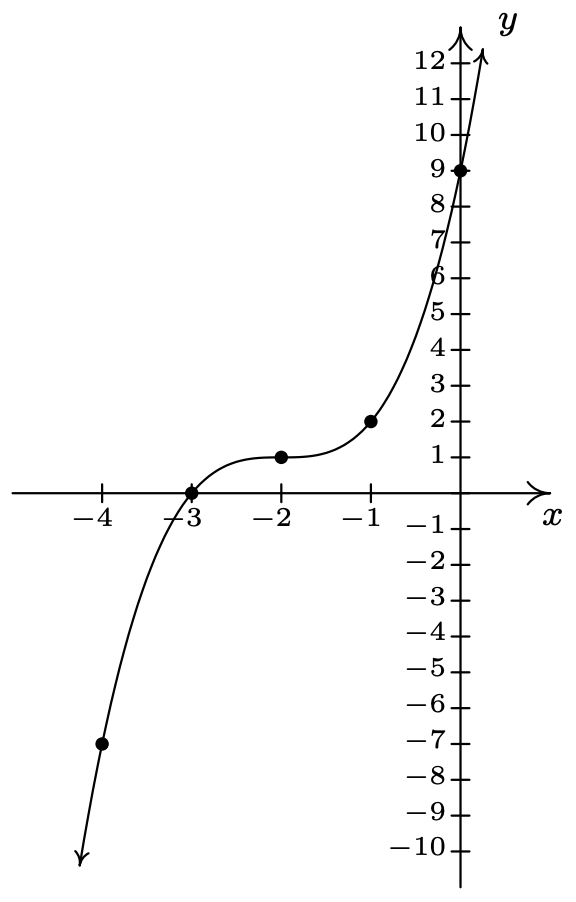

    

22. $g(x) = (x + 2)^{4} + 1$
    dominio:$(-\infty, \infty)$
    rango:$[1, \infty)$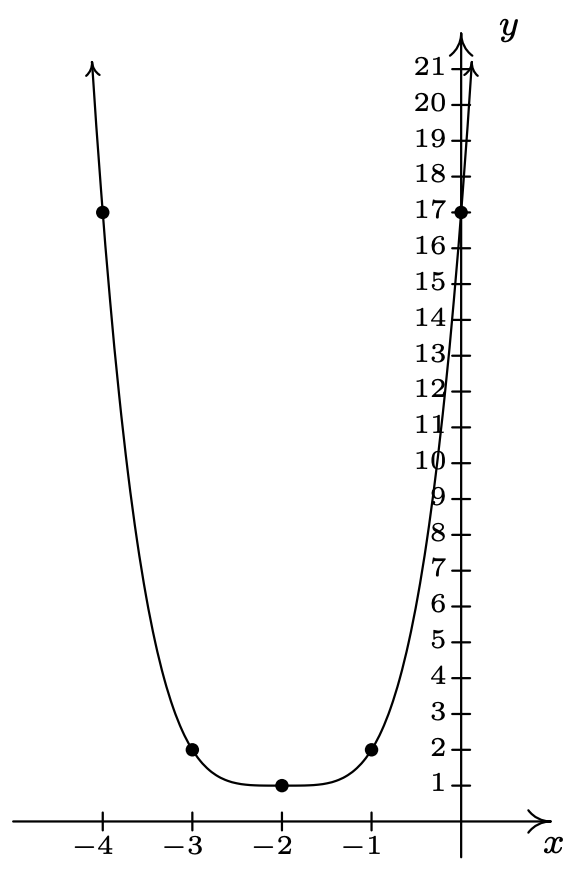

    

23. $g(x) = 2 - 3(x - 1)^{4}$
    dominio:$(-\infty, \infty)$
    rango:$(-\infty, 2]$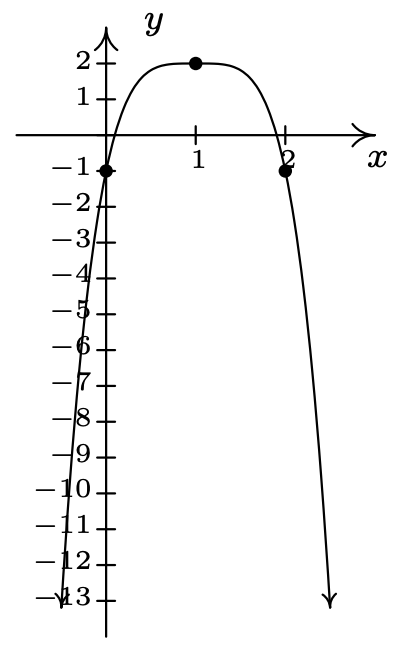

    

24. $g(x) = -x^{5} - 3$
    dominio:$(-\infty, \infty)$
    rango:$(-\infty, \infty)$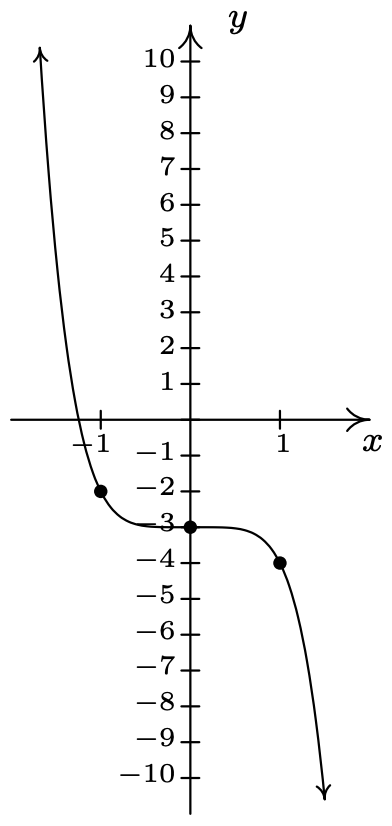

    

25. $g(x) = (x+1)^5+10$
    domain: $(-\infty, \infty)$
    range: $(-\infty, \infty)$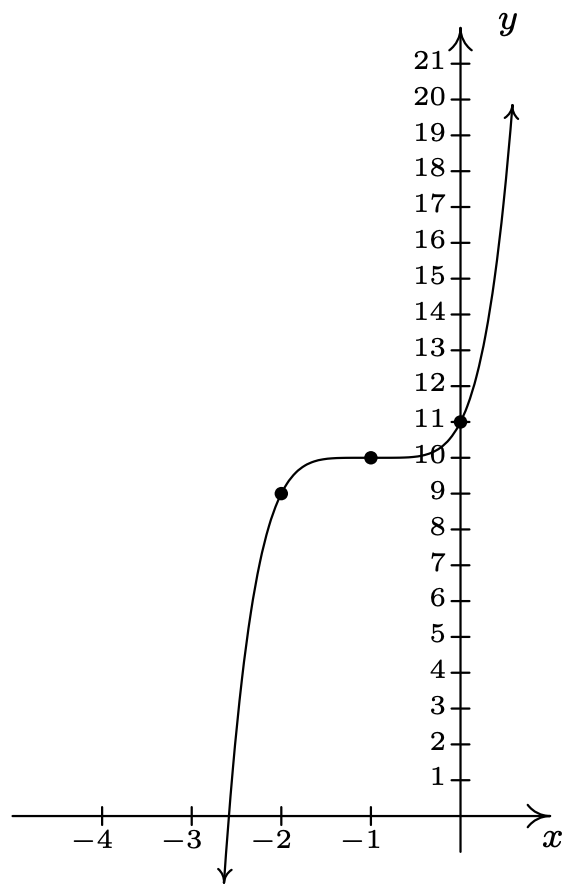

    

26. $g(x) = 8-x^{6}$
    domain: $(-\infty, \infty)$
    range: $(-\infty, 8]$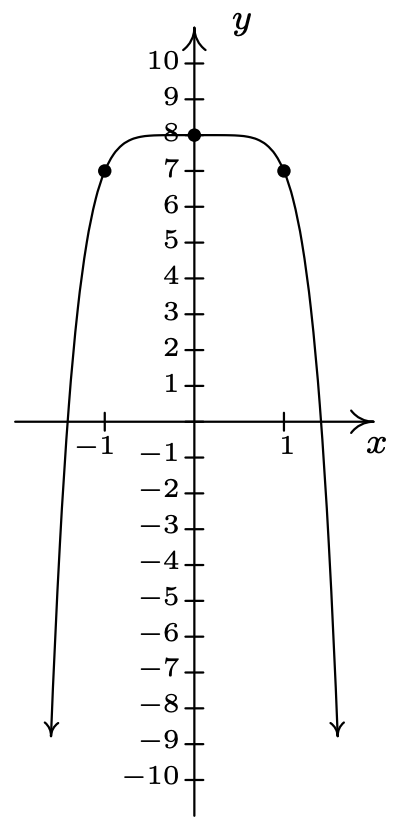

    

27. We have $f(-4)=-23,\; f(-3)=5,\; f(0)=5,\; f(1)=-3,\; f(2)=-5\;$ and $f(3)=5$ so the Intermediate Value Theorem tells us that $f(x) = x^{3} - 9x + 5$ has real zeros in the intervals $[-4, -3], [0, 1]$ and $[2, 3]$.
28. $V(x) = x(8.5-2x)(11-2x) = 4x^3-39x^2+93.5x$, $0 < x < 4.25$. Volume is maximized when $x \approx 1.58$, so the dimensions of the box with maximum volume are: height $\approx$ 1.58 inches, width $\approx$ 5.34 inches, and depth $\approx$ 7.84 inches. The maximum volume is $\approx$ 66.15 cubic inches.
29. The calculator gives the location of the absolute maximum (rounded to three decimal places) as $x \approx 6.305$ and $y \approx 1115.417$. Since $x$ represents the number of TVs sold in hundreds, $x = 6.305$ corresponds to $630.5$ TVs. Since we can’t sell half of a TV, we compare $R(6.30) \approx 1115.415$ and $R(6.31) \approx 1115.416$, so selling $631$ TVs results in a (slightly) higher revenue. Since $y$ represents the revenue in thousands of dollars, the maximum revenue is $\$ 1,\!115,\!416$.
30. $P(x) = R(x) - C(x) = -5x^3+35x^2-45x-25$, $0 \leq x \leq 10.07$.
31. The calculator gives the location of the absolute maximum (rounded to three decimal places) as $x \approx 3.897$ and $y \approx 35.255$. Since $x$ represents the number of TVs sold in hundreds, $x = 3.897$ corresponds to $389.7$ TVs. Since we can’t sell $0.7$ of a TV, we compare $P(3.89) \approx 35.254$ and $P(3.90) \approx 35.255$, so selling $390$ TVs results in a (slightly) higher revenue. Since $y$ represents the revenue in thousands of dollars, the maximum revenue is $\$ 35,\!255$.
32. Making and selling 71 PortaBoys yields a maximized profit of $5910.67.
33. 1. Our ultimate goal is to maximize the volume, so we’ll start with the maximum Length $+$ Girth of $130.$ This means the length is $130 - 4x$. The volume of a rectangular box is always length $\times$ width $\times$ height so we get $V(x) = x^{2}(130 - 4x) = -4x^{3} + 130x^{2}$.
    2. Graphing $y = V(x)$ on $[0, 33] \times [0, 21000]$ shows a maximum at $(21.67, 20342.59)$ so the dimensions of the box with maximum volume are $21.67\mbox{in.} \times 21.67\mbox{in.} \times 43.32\mbox{in.}$ for a volume of $20342.59\mbox{in.}^{3}$.
    3. If we start with Length $+$ Girth $= 108$ then the length is $108 - 4x$ and the volume is $V(x) = -4x^{3} + 108x^{2}$. Graphing $y = V(x)$ on $[0, 27] \times [0, 11700]$ shows a maximum at $(18.00, 11664.00)$ so the dimensions of the box with maximum volume are $18.00\mbox{in.} \times 18.00\mbox{in.} \times 36\mbox{in.}$ for a volume of $11664.00\mbox{in.}^{3}$. (Calculus will confirm that the measurements which maximize the volume are 18in. by 18in. by 36in., however, as I’m sure you are aware by now, we treat all calculator results as approximations and list them as such.)
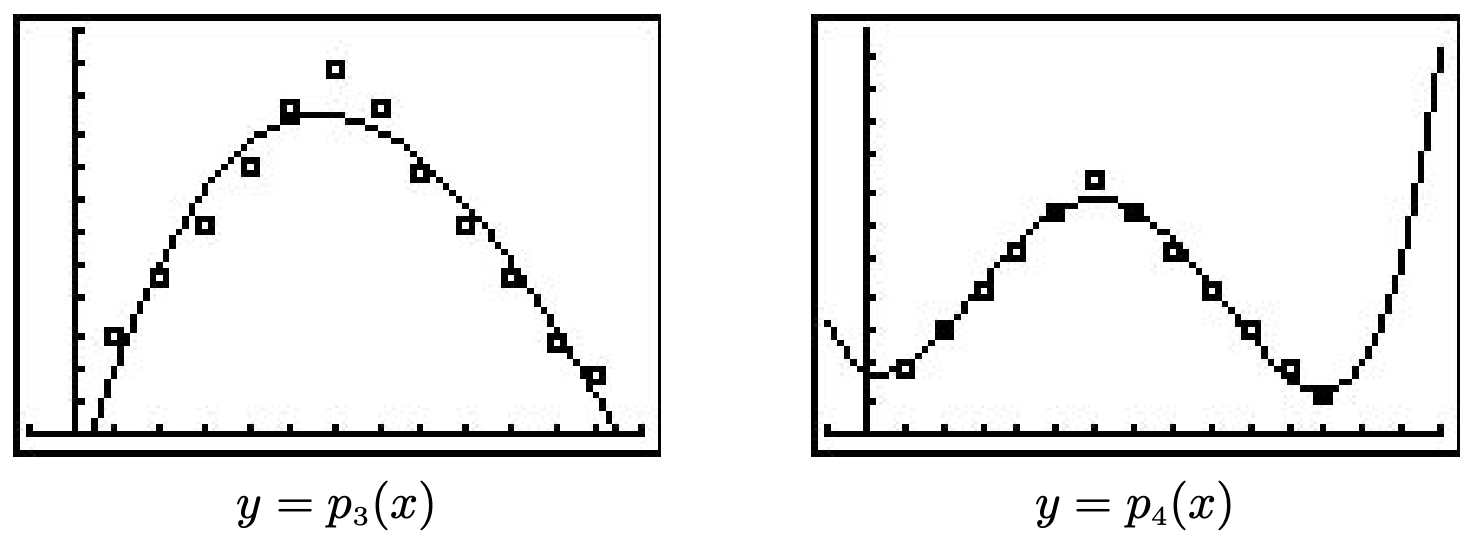
34. The cubic regression model is $p_{3}(x) = 0.0226x^{3} - 0.9508x^{2} + 8.615x - 3.446$. It has $R^{2} = 0.93765$ which isn’t bad. The graph of $y = p_{3}(x)$ in the viewing window $[-1,13] \times [0, 24]$ along with the scatter plot is shown below on the left. Notice that $p_{3}$ hits the $x$-axis at about $x = 12.45$ making this a bad model for future predictions. To use the model to approximate the number of hours of sunlight on your birthday, you’ll have to figure out what decimal value of $x$ is close enough to your birthday and then plug it into the model. My (Jeff’s) birthday is July 31 which is 10 days after July 21 ($x = 7$). Assuming 30 days in a month, I think $x = 7.33$ should work for my birthday and $p_{3}(7.33) \approx 17.5$. The website says there will be about $18.25$ hours of daylight that day. To have 14 hours of darkness we need 10 hours of daylight. We see that $p_{3}(1.96) \approx 10$ and $p_{3}(10.05) \approx 10$ so it seems reasonable to say that we’ll have at least 14 hours of darkness from December 21, 2008 ($x = 0$) to February 21, 2009 ($x = 2$) and then again from October 21,2009 ($x = 10$) to December 21, 2009 ($x = 12$).

    The quartic regression model is $p_{4}(x) = 0.0144x^{4} - 0.3507x^{3} + 2.259x^{2} - 1.571x + 5.513$. It has $R^{2} = 0.98594$ which is good. The graph of $y = p_{4}(x)$ in the viewing window $[-1, 15] \times [0, 35]$ along with the scatter plot is shown below on the right. Notice that $p_{4}(15)$ is above $24$ making this a bad model as well for future predictions. However, $p_{4}(7.33) \approx 18.71$ making it much better at predicting the hours of daylight on July 31 (my birthday). This model says we’ll have at least 14 hours of darkness from December 21, 2008 ($x = 0$) to about March 1, 2009 ($x = 2.30$) and then again from October 10, 2009 ($x = 9.667$) to December 21, 2009 ($x = 12$).

    

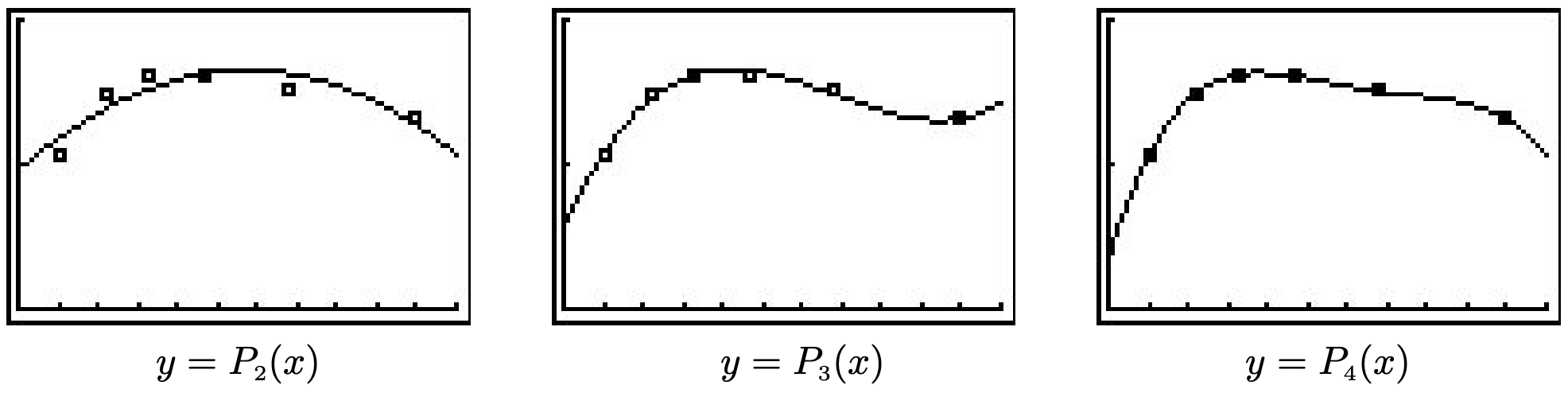
35. 1. The scatter plot is shown below with each of the three regression models.

    2. The quadratic model is $P_{2}(x) = -0.02x^{2} + 0.241x + 0.956$ with $R^{2} = 0.77708$.
       The cubic model is $P_{3}(x) = 0.005x^{3} - 0.103x^{2} + 0.602x + 0.573$ with $R^{2} = 0.98153$.
       The quartic model is $P_{4}(x) = -0.000969x^{4} + 0.0253x^{3} - 0.240x^{2} + 0.944x + 0.330$ with $R^{2} = 0.99929$.

    3. The maximums predicted by the three models are $P_{2}(5.737) \approx 1.648$, $P_{3}(4.232) \approx 1.657$ and $P_{4}(3.784) \approx 1.630$, respectively.

---

Reference

¹ Enjoy this while it lasts. Before we’re through with the book, you’ll have been exposed to the most terrible of algebraic beasts. We will tame them all, in time.

² One which really relies on Calculus to verify.

³ Technically, $\ 0^{0}$ is an indeterminant form, which is a special case of being undefined. The authors realize this is beyond pedantry, but we wouldn’t mention it if we didn’t feel it was neccessary.

⁴ this is a dangerous word...

⁵ There’s no harm in taking an extra step here and making sure this makes sense. If we chopped out a 1 inch square from each side, then the width would be 8 inches, so chopping out $\ x$ inches would leave $\ 10 − 2x$ inches.

⁶ When we write $\ V (x)$, it is in the context of function notation, not the volume $V$ times the quantity $x$.

⁷ Make sure you choose some $\ x$-values between −1 and 1.

⁸ Herein lies one of the possible origins of the term ‘even’ when applied to functions.

⁹ Of course, there are no ends to the $x$-axis.

¹⁰ We think of $x$ as becoming a very large (in the sense of its absolute value) negative number far to the left of zero.

¹¹ We think of x as moving far to the right of zero and becoming a very large positive number.

¹² See Theorems 1.4 and 1.5 in Section 1.7.

¹³ And are, perhaps, the inspiration for the moniker ‘odd function’.

¹⁴ In fact, if you take Calculus, you’ll find that smooth functions are automatically continuous, so that saying ‘polynomials are continuous and smooth’ is redundant.

¹⁵ Obtaining the factored form of a polynomial is the main focus of the next few section

¹⁶ Consider decorating the box and presenting it to your instructor. If done well enough, maybe your instructor will issue you some bonus points. Or maybe not.

¹⁷ The authors wish to thank Don Anthan and Ken White of Lakeland Community College for devising this problem and generating the accompanying data set.

¹⁸ Remember, to be a linear function, $\ m \neq 0$.