4.2: Gráficas de Funciones Racionales

En esta sección, echamos un vistazo más de cerca a graficar funciones racionales. En la Sección 4.1 aprendimos que las gráficas de funciones racionales pueden tener agujeros en ellas y podrían tener asíntotas verticales, horizontales e inclinadas. Los teoremas 4.1, 4.2 y 4.3 nos dicen exactamente cuándo y dónde ocurrirán estos comportamientos, y si combinamos estos resultados con lo que ya sabemos de graficar funciones, rápidamente podremos generar gráficas razonables de funciones racionales.

Una de las herramientas estándar que usaremos es el diagrama de signos que se introdujo primero en la Sección 2.4 y luego se revisó en la Sección 3.1. En esas secciones, operamos bajo la creencia de que una función no podía cambiar su signo sin que su gráfica cruzara por el\(x\) eje -eje. El teorema mayor que utilizamos para justificar esta creencia fue el Teorema del Valor Intermedio, Teorema 3.1. Resulta que el Teorema del Valor Intermedio se aplica a todas las funciones continuas, ¹ no solo a los polinomios. Aunque las funciones racionales son continuas en sus dominios, ² El Teorema 4.1 nos dice que las asíntotas verticales y los agujeros ocurren en los valores excluidos de sus dominios. En otras palabras, las funciones racionales no son continuas en estos valores excluidos, lo que deja abierta la posibilidad de que la función pueda cambiar de signo sin atravesar el\(x\) eje -eje. Considera la gráfica\(y=h(x)\) del Ejemplo 4.1.1, registrada a continuación para mayor comodidad. Hemos agregado su\(x\) -intercepción en\(\left(\frac{1}{2},0\right)\) para la discusión que sigue. Supongamos que deseamos construir un diagrama de signos para\(h(x)\). Recordemos que los intervalos donde\(h(x)>0\), o\((+)\), corresponden a los\(x\) -valores donde la gráfica de\(y=h(x)\) está por encima del\(x\) eje -; los intervalos en los que\(h(x) < 0\), o\((-)\) corresponden a donde la gráfica está por debajo del\(x\) eje -eje.

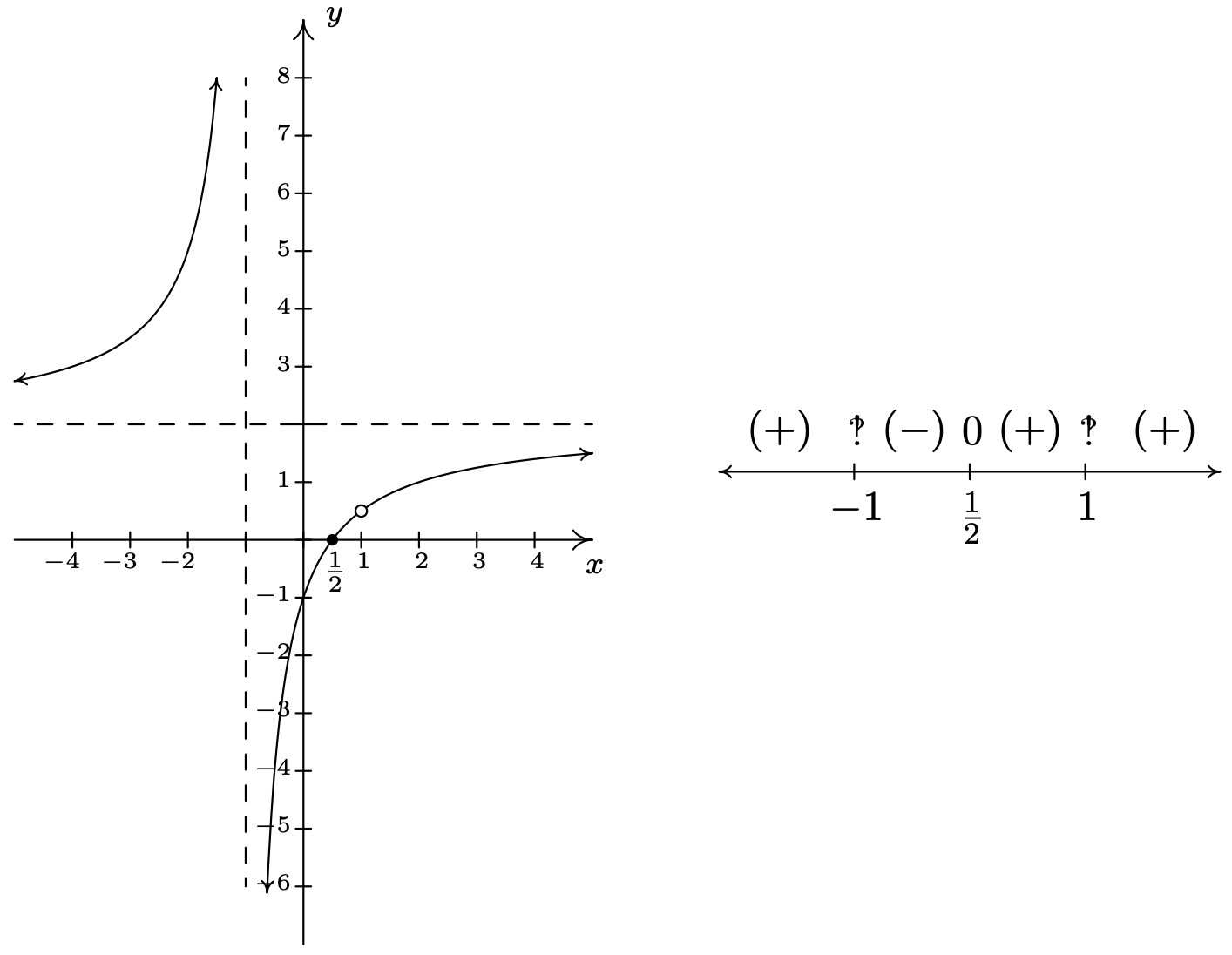
A medida que examinamos la gráfica de\(y=h(x)\), leyendo de izquierda a derecha, observamos que de\((-\infty,-1)\), la gráfica está por encima del\(x\) eje -eje, así\(h(x)\) está\((+)\) ahí. En\(x=-1\), tenemos una asíntota vertical, momento en el que la gráfica 'salta' a través del\(x\) eje. En el intervalo\(\left(-1,\frac{1}{2}\right)\), la gráfica está por debajo del\(x\) eje -, así\(h(x)\) está\((-)\) ahí. La gráfica cruza a través del\(x\) eje en\(\left(\frac{1}{2},0\right)\) y permanece por encima del\(x\) eje -hasta\(x=1\), donde tenemos un 'agujero' en la gráfica. Ya que no\(h(1)\) está definido, aquí no hay señal. Entonces tenemos\(h(x)\) como\((+)\) en el intervalo\(\left(\frac{1}{2}, 1\right)\). Continuando, vemos que encendido\((1, \infty)\), la gráfica de\(y=h(x)\) está por encima del\(x\) eje -eje, así que marcamos\((+)\) ahí. Para construir un diagrama de signos a partir de esta información, no sólo necesitamos denotar el cero de\(h\), sino también los lugares no en el dominio de\(h\). Como es nuestra costumbre, escribimos '\(0\)' arriba\(\frac{1}{2}\) en el diagrama de signos para recordarnos que es un cero de\(h\). Necesitamos una notación diferente para\(-1\) y\(1\), y hemos optado por usar '!' - un símbolo no estándar llamado interrobang. Utilizamos este símbolo para transmitir una sensación de sorpresa, precaución y asombro -una actitud apropiada a tomar al acercarse a estos puntos. La moraleja de la historia es que al construir diagramas de signos para funciones racionales, incluimos los ceros así como los valores excluidos del dominio.

Pasos para construir un diagrama de signos para una función racional

Supongamos que\(r\) es una función racional.

1. Colocar cualquier valor excluido del dominio de\(r\) en la recta numérica con un ''encima de ellos.
2. Encuentra los ceros de\(r\) y colócalos en la línea numérica con el número\(0\) encima de ellos.
3. Elija un valor de prueba en cada uno de los intervalos determinados en los pasos 1 y 2.
4. Determine el signo de\(r(x)\) para cada valor de prueba en el paso 3 y escriba ese signo por encima del intervalo correspondiente

Presentamos ahora nuestro procedimiento para graficar funciones racionales y aplicarlo a algunos ejemplos exhaustivos. Tenga en cuenta que disminuimos la cantidad de detalles dados en las explicaciones a medida que avanzamos por los ejemplos. El lector debe ser capaz de rellenar cualquier dato en aquellos pasos que hemos abreviado.

Pasos para Graficar Funciones Racionales

Supongamos que\(r\) es una función racional.

1. Encuentra el dominio de\(r\).
2. Reducir\(r(x)\) a los términos más bajos, si corresponde.
3. Encuentra las\(x\) - y\(y\) -intercepciones de la gráfica de\(y=r(x)\), si existen.
4. Determinar la ubicación de las asíntotas verticales o agujeros en la gráfica, si existen. Analizar el comportamiento de a ambos\(r\) lados de las asíntotas verticales, en su caso.
5. Analizar el comportamiento final de\(r\). Encuentra la asíntota horizontal o inclinada, si existe.
6. Utilice un diagrama de señales y trazar puntos adicionales, según sea necesario, para bosquejar la gráfica de\(y=r(x)\).

Ejemplo 4.2.1

Dibuje un gráfico detallado de\(f(x) = \dfrac{3x}{x^2-4}\).

Solución. Seguimos el procedimiento de seis pasos descrito anteriormente.

1. Como de costumbre, establecemos el denominador igual a cero para obtener\(x^2 - 4 = 0\). Nos encontramos\(x = \pm 2\), así es nuestro dominio\((-\infty, -2) \cup (-2,2) \cup (2,\infty)\).
2. Para reducir\(f(x)\) a términos más bajos, factorizamos el numerador y denominador que rinde\(f(x) = \frac{3x}{(x-2)(x+2)}\). No hay factores comunes lo que significa que ya\(f(x)\) está en términos más bajos.
3. Para encontrar las\(x\) -intercepciones de la gráfica de\(y=f(x)\), establecemos\(y=f(x) = 0\). Resolviendo\(\frac{3x}{(x-2)(x+2)} = 0\) resultados en\(x=0\). Ya que\(x=0\) está en nuestro dominio,\((0,0)\) es la\(x\) -intercepción. Para encontrar la\(y\) -intercepción, establecemos\(x=0\) y encontramos\(y = f(0) = 0\), así que esa\((0,0)\) es nuestra\(y\) -intercepción también. ³
4. Los dos números excluidos del dominio de\(f\) son\(x = -2\) y\(x=2\). Como\(f(x)\) no se redujo en absoluto, ambos valores de\(x\) siguen causando problemas en el denominador. Así por el Teorema 4.1,\(x=-2\) y\(x=2\) son asíntotas verticales de la gráfica. De hecho, podemos ir un paso más allá en este punto y determinar exactamente cómo la gráfica se acerca a la asíntota cerca de cada uno de estos valores. Aunque no es absolutamente necesario, ⁴ es una buena práctica para quienes se dirigen a Cálculo. Para la discusión que sigue, lo mejor es utilizar la forma factorizada de\(f(x) = \frac{3x}{(x-2)(x+2)}\).
   • El comportamiento de\(y=f(x)\) como\(x \rightarrow -2\): Supongamos\(x \rightarrow -2^{-}\). Si tuviéramos que construir una tabla de valores, usaríamos\(x\) -valores un poco menos que\(-2\), digamos\(-2.1\),\(-2.01\) y\(-2.001\). Si bien no hay ningún daño en construir realmente una mesa como lo hicimos en la Sección 4.1, queremos desarrollar un 'sentido de números' aquí. Pensemos en cada factor en la fórmula de\(f(x)\) como imaginamos sustituyendo un número como\(x=-2.000001\) en\(f(x)\). La cantidad\(3x\) estaría muy cerca de\(-6\), la cantidad\((x-2)\) estaría muy cerca de\(-4\), y el factor\((x+2)\) estaría muy cerca de\(0\). Más específicamente,\((x+2)\) sería un poco menor que\(0\), en este caso,\(-0.000001.\) Vamos a llamar a tal número un 'muy\((-)\) pequeño', 'muy pequeño' que significa cercano a cero en valor absoluto. Entonces, mentalmente\(x \rightarrow -2^{-}\), como, estimamos\[f(x) = \dfrac{3x}{(x-2)(x+2)} \approx \dfrac{-6}{(-4)\left( \mbox{very small $(-)$}\right)} = \dfrac{3}{2 \left( \mbox{very small $(-)$}\right)}\nonumber\] Ahora, cuanto más\(x\) se acerque\(-2\), más pequeño se\((x+2)\) volverá, así que aunque estemos multiplicando nuestro 'muy\((-)\) pequeño' por\(2\), el denominador seguirá haciéndose cada vez más pequeño, y seguirá siendo negativo. El resultado es una fracción cuyo numerador es positivo, pero cuyo denominador es muy pequeño y negativo. Mentalmente,\[f(x) \approx \dfrac{3}{2 \left( \mbox{very small $(-)$}\right)} \approx \dfrac{3}{\mbox{very small $(-)$}} \approx \mbox{very big $(-)$}\nonumber\] El término 'muy\((-)\) grande' significa un número con un gran valor absoluto el cual es negativo. ⁵ Lo que todo esto significa es que como\(x \rightarrow -2^{-}\),\(f(x) \rightarrow -\infty\). Ahora supongamos que queríamos determinar el comportamiento de\(f(x)\) as\(x \rightarrow -2^{+}\). Si nos imaginamos sustituyendo algo un poco más grande que\(-2\) en por\(x\), digamos\(-1.999999\), estimamos mentalmente\[f(x) \approx \dfrac{-6}{(-4)\left( \mbox{very small $(+)$}\right)} = \dfrac{3}{2 \left( \mbox{very small $(+)$}\right)} \approx \dfrac{3}{\mbox{very small $(+)$}} \approx \mbox{very big $(+)$}\nonumber\] Concluimos que como\(x \rightarrow -2^{+}\),\(f(x) \rightarrow \infty\).
   • El comportamiento de\(y=f(x)\) como\(x \rightarrow 2\): Considerar\(x \rightarrow 2^{-}\). Nos imaginamos sustituyendo\(x = 1.999999\). Aproximando\(f(x)\) como lo hicimos anteriormente, obtenemos\[f(x) \approx \dfrac{6}{\left( \mbox{very small $(-)$}\right)(4)} = \dfrac{3}{2 \left( \mbox{very small $(-)$}\right)} \approx \dfrac{3}{\mbox{very small $(-)$}} \approx \mbox{very big $(-)$}\nonumber\] Llegamos a la conclusión de que como\(x \rightarrow 2^{-}\),\(f(x) \rightarrow -\infty\). De igual manera, como\(x \rightarrow 2^{+}\), nos imaginamos sustituyendo\(x = 2.000001\) para conseguir\(f(x) \approx \frac{3}{\text { very small }(+)} \approx \text { very big }(+)\). Así como\(x \rightarrow 2^{+}, f(x) \rightarrow \infty\).

   Gráficamente, tenemos eso cerca\(x=-2\) y\(x=2\) la gráfica de\(y=f(x)\) parece ⁶

   

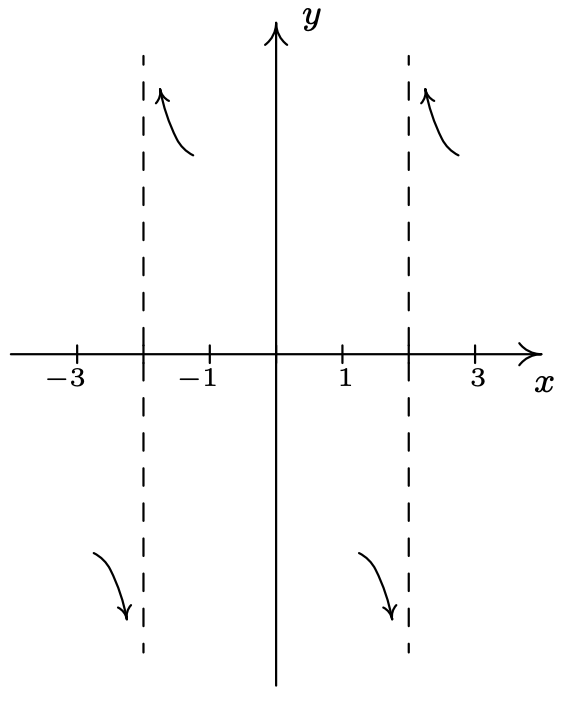
5. A continuación, determinamos el comportamiento final de la gráfica de\(y=f(x)\). Ya que el grado del numerador es\(1\), y el grado del denominador es\(2\), el Teorema 4.2 nos dice que\(y=0\) es la asíntota horizontal. Al igual que con las asíntotas verticales, podemos obtener información más detallada utilizando el 'sentido de número'. Para la discusión a continuación, utilizamos la fórmula\(f(x) = \frac{3x}{x^2-4}\).
   • El comportamiento de\(y=f(x)\) as\(x \rightarrow -\infty\): Si tuviéramos que hacer una tabla de valores para discutir el comportamiento de\(f\) as\(x \rightarrow -\infty\), sustituiríamos números negativos muy 'grandes' en\(x\), digamos por ejemplo,\(x = billion\). El numerador\(3x\) sería entonces\(-3 \, \mbox{billion}\), mientras que el denominador\(x^2-4\) sería\((billion)^2 - 4\), que es más o menos lo mismo que\(1(\mbox{billion})^2\). De ahí que,\[f\left(\mbox{$-1$ billion}\right) \approx \dfrac{-3 \, \mbox{billion}}{1(\mbox{billion})^2} \approx - \dfrac{3}{\mbox{billion}} \approx \mbox{very small $(-)$}\nonumber\]
   • El comportamiento de\(y=f(x)\) como\(x \rightarrow \infty\): Por otro lado, podemos imaginar sustituyendo números positivos muy grandes en por\(x\) y mirando el comportamiento de\(f(x)\). Por ejemplo, vamos\(x = 1\, billion\). Procediendo como antes, obtenemos\[f\left(\mbox{$1$ billion}\right) \approx \dfrac{3 \, \mbox{billion}}{1(\mbox{billion})^2} \approx \dfrac{3}{\mbox{billion}} \approx \mbox{very small $(+)$}\nonumber\] Cuanto mayor sea el número que metemos, menor será el número positivo que saldríamos. En otras palabras, as\(x \rightarrow \infty\),\(f(x) \rightarrow 0^{+}\), así que la gráfica de\(y=f(x)\) está un poco por encima del\(x\) eje -conforme miramos hacia el extremo derecho.

   Gráficamente, tenemos ⁷

   

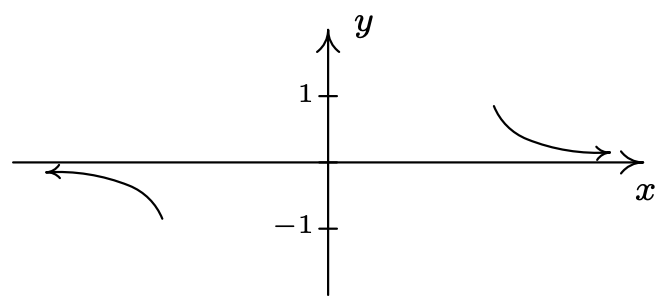
6. Por último, construimos un diagrama de signos para\(f(x)\). Los\(x\) -valores excluidos del dominio de\(f\) son\(x = \pm 2\), y el único cero de\(f\) es\(x=0\). Mostrarlos apropiadamente en la recta numérica nos da cuatro intervalos de prueba, y elegimos los valores de prueba ⁸\(x=-3\),\(x=-1\),\(x=1\) y\(x=3\). Encontramos\(f(-3)\) es\((-)\),\(f(-1)\) es\((+)\),\(f(1)\) es\((-)\) y\(f(3)\) es\((+)\). Combinando esto con nuestro trabajo anterior, obtenemos la gráfica de\(y=f(x)\) abajo.

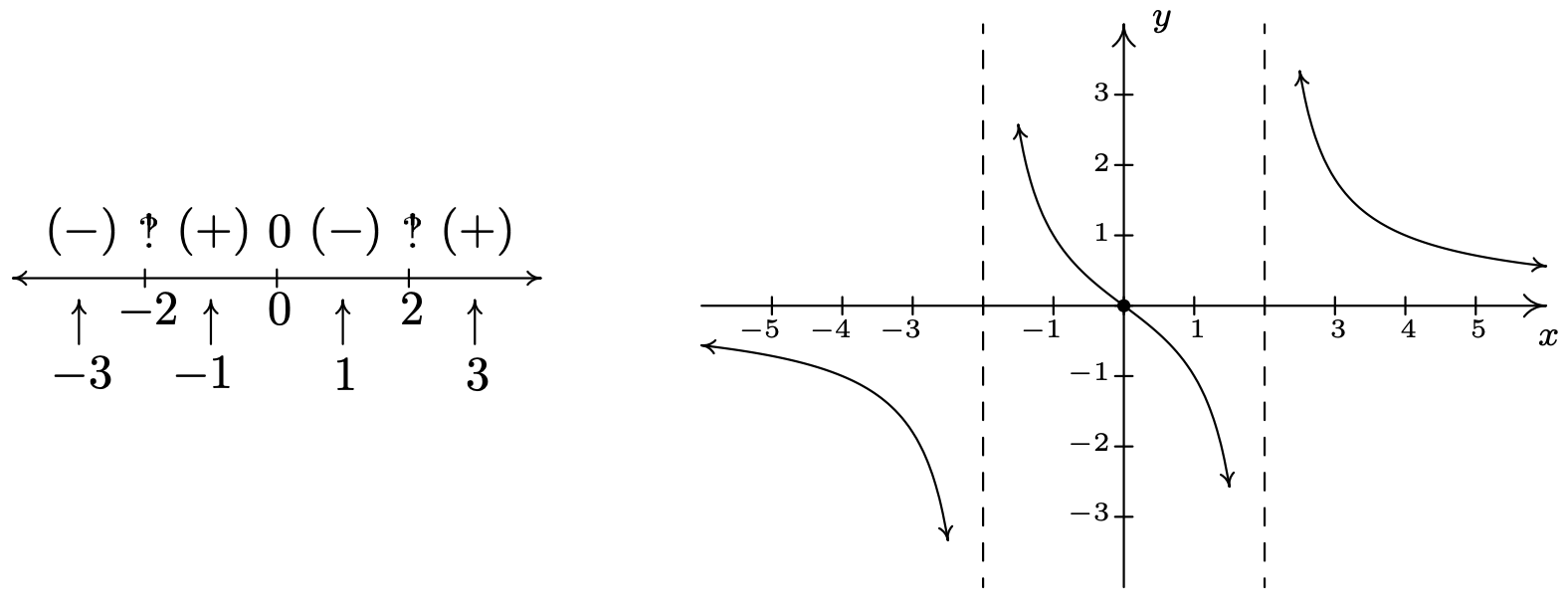
Un par de notas están en orden. En primer lugar, la gráfica de\(y=f(x)\) ciertamente parece poseer simetría con respecto al origen. De hecho, podemos comprobar\(f(-x) = -f(x)\) para ver que\(f\) es una función impar. En algunos libros de texto, verificar la simetría es parte del procedimiento estándar para graficar funciones racionales; pero como ocurre comparativamente raramente ⁹ solo lo señalaremos cuando lo veamos. También tenga en cuenta que si bien\(y=0\) es la asíntota horizontal, la gráfica de\(f\) realmente cruza el\(x\) eje en\((0,0)\). El mito de que las gráficas de funciones racionales no pueden cruzar sus asíntotas horizontales es completamente falso, ¹⁰ como volveremos a ver en nuestro siguiente ejemplo.

Ejemplo 4.2.2

Dibuje un gráfico detallado de\(g(x) = \dfrac{2x^2-3x-5}{x^2-x-6}\).

Solución.

1. Ajuste\(x^2-x-6 = 0\) da\(x = -2\) y\(x=3\). Nuestro dominio es\((-\infty, -2) \cup (-2,3) \cup (3,\infty)\).
2. Factoring\(g(x)\) da\(g(x) = \frac{(2x-5)(x+1)}{(x-3)(x+2)}\). No hay cancelación, por lo que\(g(x)\) es en términos más bajos.
3. Para encontrar la\(x\) -intercepción que establecemos\(y = g(x) = 0\). Usando la forma factorizada de\(g(x)\) arriba, encontramos que los ceros son las soluciones de\((2x-5)(x+1)=0\). Obtenemos\(x = \frac{5}{2}\) y\(x=-1\). Dado que ambos números están en el dominio de\(g\), tenemos dos\(x\) -intercepciones,\(\left( \frac{5}{2},0\right)\) y\((-1,0)\). Para encontrar la\(y\) -intercepción, establecemos\(x=0\) y encontramos\(y = g(0) = \frac{5}{6}\), entonces nuestra\(y\) -intercepción es\(\left(0, \frac{5}{6}\right)\).
4. Ya que nos\(g(x)\) fue dado en términos más bajos, tenemos, una vez más por el Teorema 4.1 asíntotas verticales\(x=-2\) y\(x=3\). Teniendo en cuenta\(g(x) = \frac{(2x-5)(x+1)}{(x-3)(x+2)}\), procedemos a nuestro análisis cerca de cada uno de estos valores.
   • El comportamiento de\(y=g(x)\) as\(x \rightarrow -2\): As\(x \rightarrow -2^{-}\), imaginamos sustituyendo un número un poco menos que\(-2\). Tenemos\[g(x) \approx \frac{(-9)(-1)}{(-5)(\mbox{very small $(-)$})} \approx \frac{9}{\mbox{very small $(+)$}} \approx \mbox{very big (+)}\nonumber\] así como\(x \rightarrow -2^{-}\),\(g(x) \rightarrow \infty\). Por otro lado, como\(x \rightarrow -2^{+}\),\[g(x) \approx \frac{9}{\mbox{ very small $(-)$}} \approx \mbox{very big $(-)$}\nonumber\] así lo conseguimos\(g(x) \rightarrow -\infty\).
   • El comportamiento de\(y=g(x)\) como\(x \rightarrow 3\): Como\(x \rightarrow 3^{-}\), imaginamos enchufar un número apenas tímido de\(3\). Tenemos\[g(x) \approx \frac{(1)(4)}{(\mbox{ very small $(-)$}) (5)} \approx \frac{4}{\mbox{very small $(-)$}} \approx \mbox{very big $(-)$}\nonumber\] De ahí, como\(x \rightarrow 3^{-}\),\(g(x) \rightarrow -\infty\). Como\(x \rightarrow 3^{+}\),\[g(x) \approx \frac{4}{\mbox{ very small $(+)$}} \approx \mbox{very big $(+)$}\nonumber\] así lo conseguimos\(g(x) \rightarrow \infty\).

   Gráficamente, tenemos (de nuevo, sin etiquetas en el\(y\) eje -axis)

   

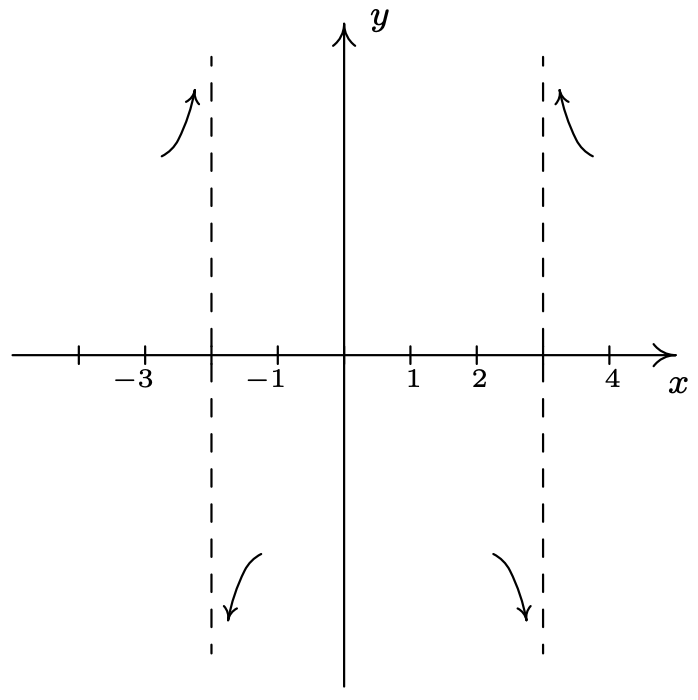
5. Ya que los grados del numerador y denominador de\(g(x)\) son los mismos, sabemos por el Teorema 4.2 que podemos encontrar la asíntota horizontal de la gráfica de\(g\) tomando la relación de los términos principales coeficientes,\(y = \frac{2}{1} = 2\). Sin embargo, si nos tomamos el tiempo para hacer un análisis más detallado, podremos revelar algún comportamiento 'oculto' que de otra manera se perdería. ¹¹ Al igual que en la discusión que sigue al Teorema 4.2, utilizamos el resultado de la división larga\(\left(2x^2-3x-5\right) \div \left(x^2-x-6\right)\) para reescribir\(g(x) = \frac{2x^2-3x-5}{x^2-x-6}\) ya\(g(x) = 2 - \frac{x-7}{x^2-x-6}.\) que enfocamos nuestra atención en el término\(\frac{x-7}{x^2-x-6}\).
   • El comportamiento de\(y=g(x)\) como\(x \rightarrow -\infty\): Si imaginamos sustituyendo\(x = billion\) en\(\frac{x-7}{x^2-x-6}\), estimamos\(\frac{x-7}{x^{2}-x-6} \approx \frac{-1 \text { billion }}{1 \text { billion }^{2}} \approx \text { very small }(-)\). ¹² De ahí que,\[g(x) = 2 - \frac{x-7}{x^2-x-6} \approx 2 - \mbox{very small $(-)$} = 2 + \mbox{very small $(+)$}\nonumber\] en otras palabras, como\(x \rightarrow -\infty\), la gráfica de\(y=g(x)\) está un poco por encima de la línea\(y=2\).
   • El comportamiento de\(y=g(x)\) as\(x \rightarrow \infty\). A considerar\(\frac{x-7}{x^2-x-6}\) como\(x \rightarrow \infty\), nos imaginamos sustituyendo\(x = 1\, billion\) y, pasando por la rutina mental habitual, encontramos\[\frac{x-7}{x^2-x-6} \approx \mbox{very small $(+)$}\nonumber\] De ahí que\(g(x) \approx 2-\text { very small }(+)\), en otras palabras, la gráfica de\(y=g(x)\) está justo debajo de la línea\(y=2\) como\(x \rightarrow \infty\).

   On\(y=g(x)\), tenemos (de nuevo, sin etiquetas en el\(x\) eje -axis)

   

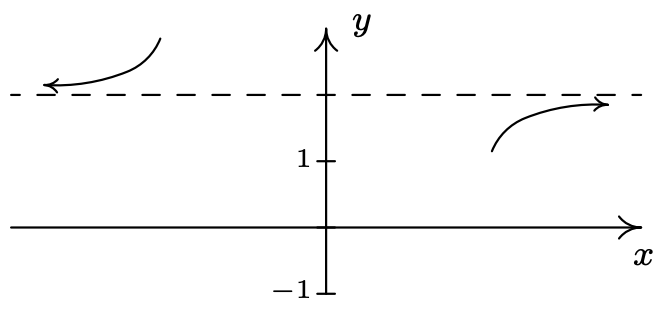
6. Finalmente construimos nuestro diagrama de signos. Colocamos un ''arriba\(x=-2\) y\(x=3\), y un '\(0\)' arriba\(x = \frac{5}{2}\) y\(x=-1\). Elegir valores de prueba en los intervalos de prueba nos da\(f(x)\) es\((+)\) en los intervalos\((-\infty, -2)\),\(\left(-1, \frac{5}{2}\right)\) y\((3, \infty)\), y\((-)\) en los intervalos\((-2,-1)\) y\(\left(\frac{5}{2}, 3\right)\). A medida que juntamos toda la información, observamos que la gráfica debe cruzar la asíntota horizontal\(x=3\) en algún momento posterior para que se acerque\(y=2\) desde abajo. Esta es la sutileza que nos habríamos perdido si nos hubiéramos saltado la división larga y el posterior análisis de comportamiento final. Podemos, de hecho, encontrar exactamente cuándo cruza la gráfica\(y=2\). Como resultado de la larga división, tenemos\(g(x) = 2 - \frac{x-7}{x^2-x-6}\). Porque\(g(x) = 2\), necesitaríamos\(\frac{x-7}{x^2-x-6} = 0\). Esto da\(x-7= 0\), o\(x=7\). Tenga en cuenta que\(x-7\) es el resto cuando\(2x^2-3x-5\) se divide por\(x^2-x-6\), por lo que tiene sentido que\(g(x)\) para igualar el cociente\(2\), el resto de la división debe ser\(0\). Bastante seguro, nos encontramos\(g(7)=2\). Además, es lógico pensar que\(g\) debe alcanzar un mínimo relativo en algún momento pasado\(x=7\). Cálculo verifica que en\(x=13\), tenemos tal mínimo en exactamente\((13, 1.96)\). El lector tiene el reto de encontrar ventanas de calculadora que muestren la gráfica cruzando su asíntota horizontal en una ventana, y el mínimo relativo en la otra.

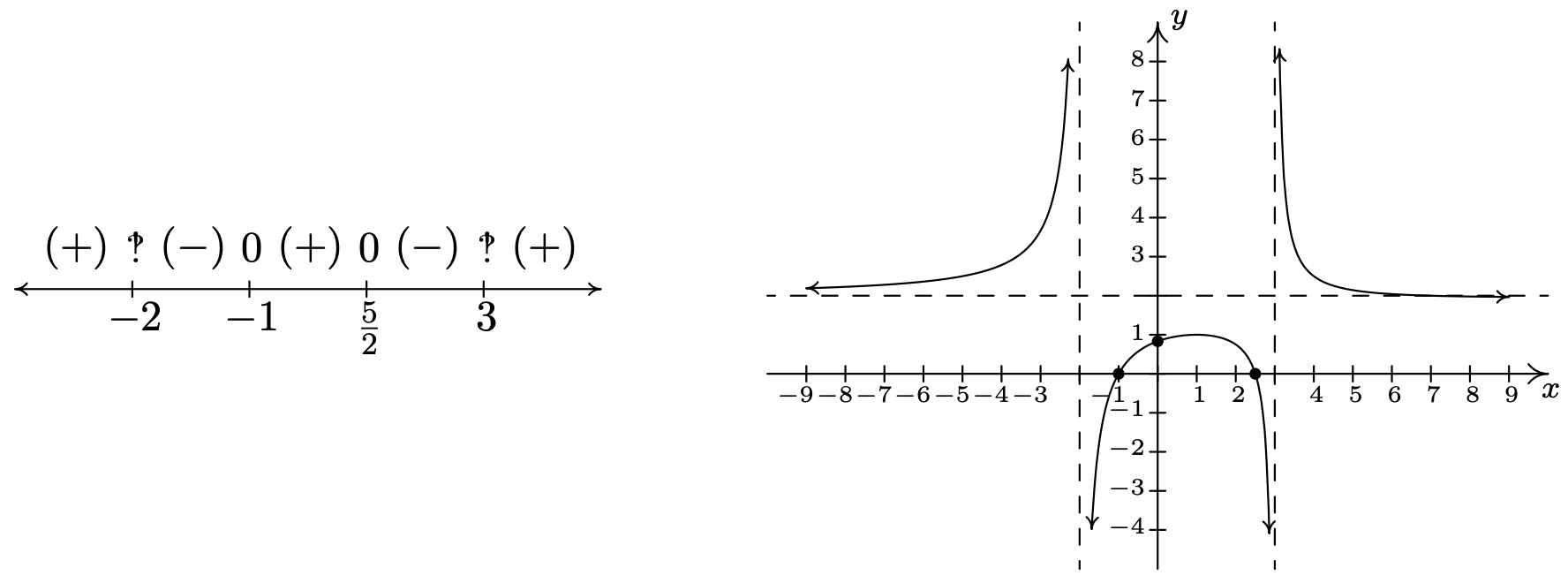
Nuestro siguiente ejemplo nos da la oportunidad de analizar más a fondo una asíntota inclinada.

Ejemplo 4.2.3

Dibuje un gráfico detallado de\(h(x) = \dfrac{2x^3+5x^2+4x+1}{x^2+3x+2}\).

Solución.

1. Para dominio, ya conoces el simulacro. Resolviendo\(x^2+3x+2 = 0\) da\(x = -2\) y\(x=-1\). Nuestra respuesta es\((-\infty, -2) \cup (-2, -1) \cup (-1, \infty)\).
2. Para reducir\(h(x)\), necesitamos factorial el numerador y el denominador. Para factorizar el numerador, utilizamos las técnicas ¹³ establecidas en la Sección 3.3 y\[h(x) = \dfrac{2x^3+5x^2+4x+1}{x^2+3x+2} = \dfrac{(2x+1)(x+1)^2}{(x+2)(x+1)} = \dfrac{ (2x+1) (x+1)^{\cancelto{1}{2}} }{(x+2)\cancel{(x+1)}} = \dfrac{(2x+1)(x+1)}{x+2}\nonumber\] obtenemos Vamos a utilizar esta fórmula reducida\(h(x)\) mientras no estemos sustituyendo\(x = −1\). Para hacer específica esta exclusión, escribimos\(h(x)=\frac{(2 x+1)(x+1)}{x+2}, x \neq-1\).
3. Para encontrar las\(x\) -intercepciones, como de costumbre, establecemos\(h(x) = 0\) y resolvemos. Resolviendo\(\frac{(2x+1)(x+1)}{x+2}=0\) rendimientos\(x=-\frac{1}{2}\) y\(x=-1\). Este último no está en el dominio de\(h\), por lo que lo excluimos. Nuestra única\(x\) intercepción es\(\left(-\frac{1}{2}, 0\right)\). Para encontrar la\(y\) -intercepción, nos fijamos\(x=0\). Ya que\(0 \neq -1\), podemos usar la fórmula reducida para\(h(x)\) y obtenemos\(h(0) = \frac{1}{2}\) para una\(y\) -intercepción de\(\left(0,\frac{1}{2}\right)\).
4. Del Teorema 4.1, sabemos que como\(x=-2\) todavía plantea una amenaza en el denominador de la función reducida, tenemos ahí una asíntota vertical. En cuanto a\(x=-1\), el factor\((x+1)\) se canceló del denominador cuando reducimos\(h(x)\), por lo que ya no causa problemas ahí. Esto quiere decir que nos sale un agujero cuando\(x=-1\). Para encontrar la\(y\) coordenada -del hoyo, sustituimos\(x=-1\) en\(\frac{(2x+1)(x+1)}{x+2}\), por Teorema 4.1 y obtenemos\(0\). Por lo tanto, tenemos un agujero en el\(x\) eje -en\((-1,0)\). Debería hacerte sentir incómodo conectarte\(x=-1\) a la fórmula reducida para\(h(x)\), especialmente porque hemos hecho un gran problema con respecto a la estipulación de no permitir\(x=-1\) esa fórmula. Lo que realmente estamos haciendo es llevar un atajo de Cálculo al tipo de análisis más detallado cerca del\(x=-1\) cual mostraremos a continuación. Hablando de lo cual, para la discusión que sigue, usaremos la fórmula\(h(x) = \frac{(2x+1)(x+1)}{x+2}\),\(x \neq -1\).
   • El comportamiento de\(y=h(x)\) as\(x \rightarrow -2\): As\(x \rightarrow -2^{-}\), imaginamos sustituyendo un número un poco menos que\(-2\). Tenemos\(h(x) \approx \frac{(-3)(-1)}{(\text { very small }(-))} \approx \frac{3}{(\text { very small }(-))} \approx \text { very big }(-)\) así como\(x \rightarrow -2^{-}\),\(h(x) \rightarrow -\infty\). Del otro lado de\(-2\), como\(x \rightarrow -2^{+}\), nos encontramos con eso\(h(x) \approx \frac{3}{\text { very small }(+)} \approx \text { very big }(+)\), así\(h(x) \rightarrow \infty\).
   • El comportamiento de\(y=h(x)\) as\(x \rightarrow -1\). Como\(x \rightarrow -1^{-}\), imaginamos enchufar un número un poco menos que\(x=-1\). Tenemos\(h(x) \approx \frac{(-1)(\text { very small }(-))}{1}=\text { very small }(+)\) De ahí, como\(x \rightarrow -1^{-}\),\(h(x) \rightarrow 0^{+}\). Esto quiere decir que como\(x \rightarrow -1^{-}\), la gráfica está un poco por encima del punto\((-1,0)\). Como\(x \rightarrow -1^{+}\), obtenemos\(h(x) \approx \frac{(-1)(\text { very small }(+))}{1}=\text { very small }(-)\). Esto nos da que como\(x \rightarrow -1^{+}\),\(h(x) \rightarrow 0^{-}\), así la gráfica es un poco más baja que\((-1,0)\) aquí.

   Gráficamente, tenemos

   

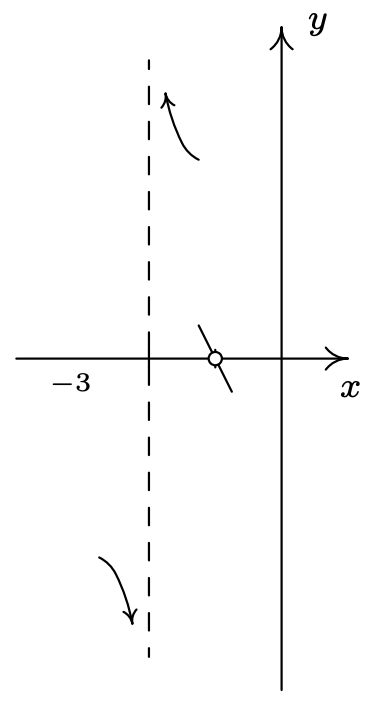
5. Para el comportamiento final, observamos que el grado del numerador de\(h(x)\),\(2x^3+5x^2+4x+1\), es\(3\) y el grado del denominador,\(x^2+3x+2\), es\(2\) así por el Teorema 4.3, la gráfica de\(y = h(x)\) tiene una asíntota inclinada. Porque\(x\rightarrow \pm \infty\), estamos lo suficientemente lejos de\(x=-1\) usar la fórmula reducida,\(h(x) = \frac{(2x+1)(x+1)}{x+2}\),\(x \neq -1\). Para realizar división larga, multiplicamos el numerador y obtenemos\(h(x) = \frac{2x^2+3x+1}{x+2}\),\(x \neq -1\), y reescribimos\(h(x) = 2x-1+\frac{3}{x+2}\),\(x \neq -1\). Por el Teorema 4.3, la asíntota inclinada es\(y = 2x-1\), y para ver mejor cómo se acerca la gráfica a la asíntota, enfocamos nuestra atención en el término generado a partir del resto,\(\frac{3}{x+2}\).
   • El comportamiento de\(y=h(x)\) como\(x \rightarrow -\infty\): Sustituyendo\(x = billion\) en\(\frac{3}{x+2}\), obtenemos la estimación\(\frac{3}{-1 \text { billion }} \approx \text { very small }(-)\). De ahí,\(h(x)=2 x-1+\frac{3}{x+2} \approx 2 x-1+\text { very small }(-)\). Esto significa que la gráfica de\(y=h(x)\) está un poco por debajo de la línea\(y=2x-1\) como\(x \rightarrow -\infty\).
   • El comportamiento de\(y=h(x)\) como\(x \rightarrow \infty\): Si\(x \rightarrow \infty\), entonces\(\frac{3}{x+2} \approx \text { very small }(+)\). Esto significa\(h(x) \approx 2 x-1+\text { very small }(+)\), o que la gráfica de\(y=h(x)\) está un poco por encima de la línea\(y=2x-1\) como\(x \rightarrow \infty\).

   Gráficamente tenemos

   

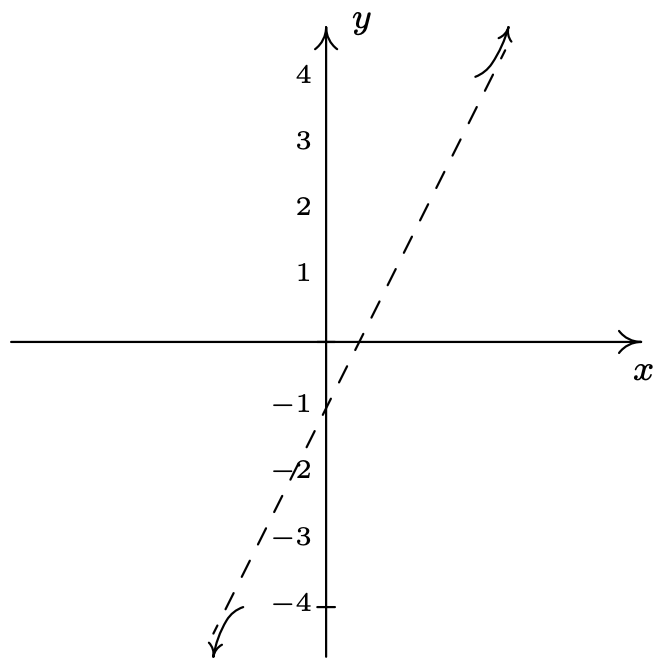
6. Para hacer nuestro diagrama de señales, colocamos un ''arriba\(x=-2\)\(x=-1\) y un '\(0\)' arriba\(x=-\frac{1}{2}\). En nuestros cuatro intervalos de prueba, encontramos que\(h(x)\) está\((+)\) encendido\((-2,-1)\) y\(\left(-\frac{1}{2}, \infty\right)\) y\(h(x)\) está\((-)\) encendido\((-\infty, -2)\) y\(\left(-1,-\frac{1}{2}\right)\). Al juntar todo nuestro trabajo se obtiene la gráfica a continuación.

   

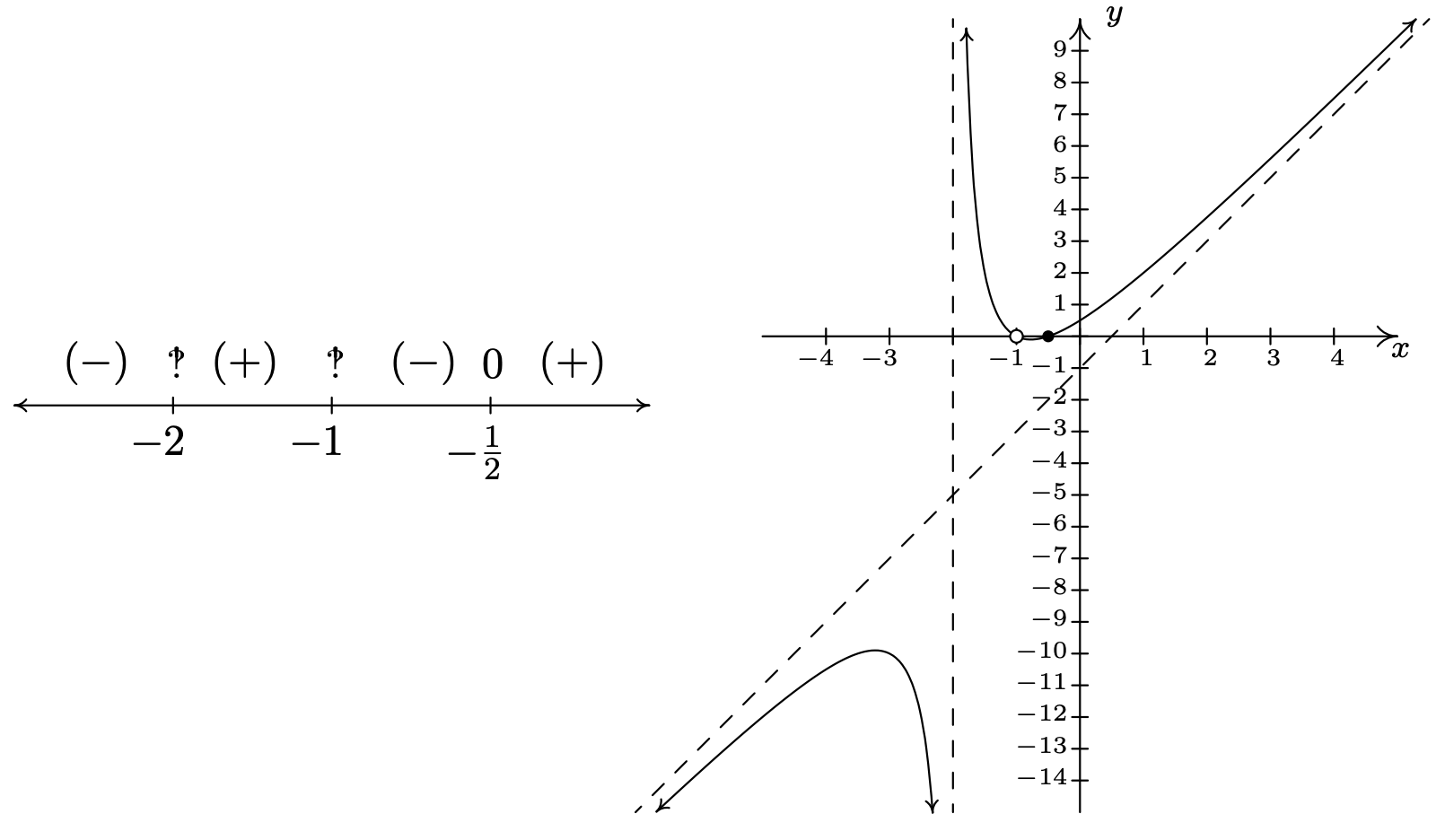
   Podríamos preguntarnos si la gráfica de\(y=h(x)\) cruza su asíntota inclinada. De la fórmula\(h(x) = 2x-1+\frac{3}{x+2}\)\(x \neq -1\),, vemos que si\(h(x) = 2x-1\), tendríamos\(\frac{3}{x+2} = 0\). Como esto nunca sucederá, concluimos que la gráfica nunca cruza su asíntota inclinada. ¹⁴

Terminamos esta sección con un ejemplo que demuestra que no todo es rareza patológica cuando se trata de funciones racionales y la tecnología todavía tiene un papel que desempeñar en el estudio de sus gráficas a este nivel.

Ejemplo 4.2.4

Esbozar la gráfica de\(r(x) = \dfrac{x^4+1}{x^2+1}\).

Solución.

1. El denominador nunca\(x^2+1\) es cero así que el dominio lo es\((-\infty, \infty)\).
2. Sin ceros reales en el denominador,\(x^2+1\) es una cuadrática irreducible. Nuestra única esperanza de reducir\(r(x)\) es si\(x^2+1\) es un factor de\(x^4+1\). Realizar división larga nos da\[\frac{x^4+1}{x^2+1} = x^2-1+\frac{2}{x^2+1}\nonumber\] El resto no es cero por lo que ya\(r(x)\) está reducido.
3. Para encontrar la\(x\) -intercepción, nos fijamos\(r(x) = 0\). Como no hay soluciones reales para\(\frac{x^4+1}{x^2+1}=0\), no tenemos\(x\) -intercepciones. Ya que\(r(0) = 1\), obtenemos\((0,1)\) como la\(y\) -intercepción.
4. Este paso no aplica a\(r\), ya que su dominio es todo números reales.
5. Para el comportamiento final, observamos que dado que el grado del numerador es exactamente dos más que el grado del denominador, no se aplican ni los Teoremas 4.2 ni 4.3. ¹⁵ Sabemos por nuestro intento de reducir\(r(x)\) que podemos reescribir\(r(x) = x^2-1+\frac{2}{x^2+1}\), por lo que enfocamos nuestra atención en el término correspondiente al resto,\(\frac{2}{x^2+1}\) Debe quedar claro que como\(x \rightarrow \pm \infty\),\(\frac{2}{x^{2}+1} \approx \text { very small }(+)\), lo que significa\(r(x) \approx x^{2}-1+\text { very small }(+)\). Entonces la gráfica\(y=r(x)\) está un poco por encima de la gráfica de la parábola\(y=x^2-1\) como\(x \rightarrow \pm \infty\). Gráficamente,

   

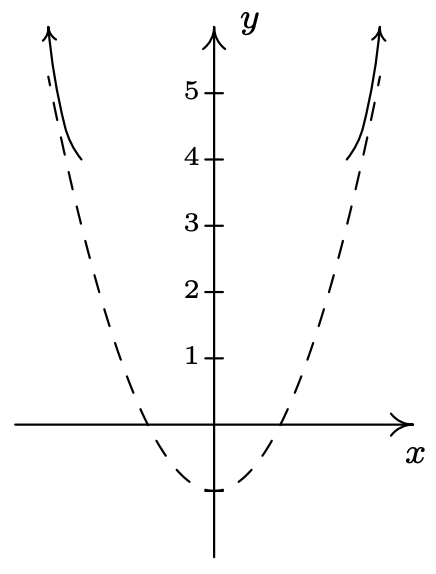
6. No hay mucho trabajo que hacer para un diagrama de señales\(r(x)\), ya que su dominio es todo números reales y no tiene ceros. Nuestro único intervalo de prueba es\((-\infty, \infty)\), y como sabemos\(r(0) = 1\), concluimos que\(r(x)\) es\((+)\) para todos los números reales. En este punto, no tenemos mucho que seguir para una gráfica. ¹⁶ A continuación se muestra una comparación de lo que hemos determinado analíticamente frente a lo que nos muestra la calculadora. No tenemos forma de detectar los extremos relativos analíticamente ¹⁷ aparte del trazado de fuerza bruta de puntos, lo que se hace de manera más eficiente por la calculadora.

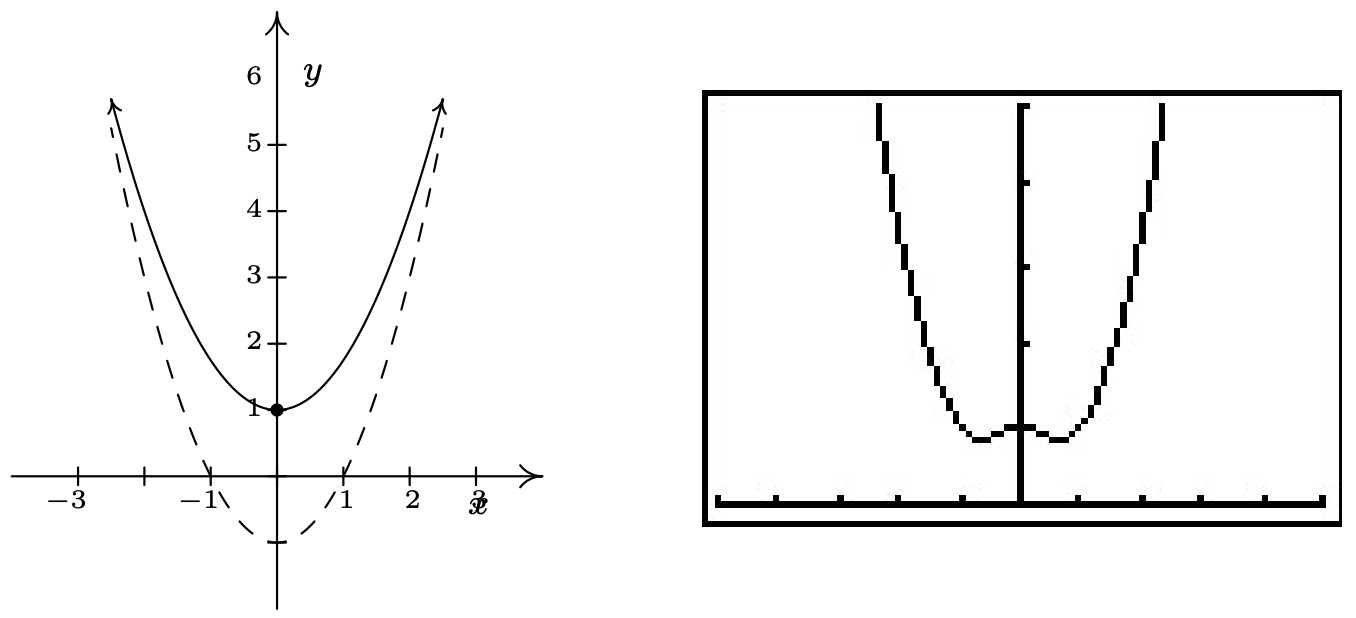
Como es habitual, los autores no ofrecen disculpas por lo que puede interpretarse como 'pedantería' en esta sección. Consideramos que el detalle presentado en esta sección es necesario para obtener una comprensión firme de los conceptos aquí presentados y también sirve como introducción a los métodos empleados en Cálculo. Como hemos dicho muchas veces en el pasado, su instructor decidirá cuántos, si los hay, de los tipos de detalles que aquí se presentan son 'críticos de misión' para su comprensión del Precálculo. Sin más dilación, te presentamos los Ejercicios de esta sección.

4.2.1 Ejercicios

En los Ejercicios 1 - 16, utilice el procedimiento de seis pasos para graficar la función racional. Asegúrese de dibujar las asíntotas como líneas discontinuas.

1. \(f(x) = \dfrac{4}{x + 2}\)
2. \(f(x) = \dfrac{5x}{6 - 2x}\)
3. \(f(x) = \dfrac{1}{x^{2}}\)
4. \(f(x) = \dfrac{1}{x^{2} + x - 12}\)
5. \(f(x) = \dfrac{2x - 1}{-2x^{2} - 5x + 3}\)
6. \(f(x) = \dfrac{x}{x^{2} + x - 12}\)
7. \(f(x) = \dfrac{4x}{x^2+4}\)
8. \(f(x) = \dfrac{4x}{x^2-4}\)
9. \(f(x) = \dfrac{x^2-x-12}{x^2+x-6}\)
10. \(f(x) = \dfrac{3x^2-5x-2}{x^2-9}\)
11. \(f(x) = \dfrac{x^2-x-6}{x+1}\)
12. \(f(x) = \dfrac{x^2-x}{3-x}\)
13. \(f(x) = \dfrac{x^3+2x^2+x}{x^2-x-2}\)
14. \(f(x) = \dfrac{-x^{3} + 4x}{x^{2} - 9}\)
15. \(f(x) = \dfrac{x^3-2x^2+3x}{2x^2+2}\)
16. ¹⁸\(f(x) = \dfrac{x^{2} - 2x + 1}{x^{3} + x^{2} - 2x}\)

En los Ejercicios 17 - 20, grafica la función racional aplicando transformaciones a la gráfica de\(y = \dfrac{1}{x}\).

17. \(f(x) = \dfrac{1}{x - 2}\)
18. \(g(x) = 1 - \dfrac{3}{x}\)
19. \(h(x) = \dfrac{-2x + 1}{x}\)(Pista: Dividir)
20. \(j(x) = \dfrac{3x - 7}{x - 2}\)(Pista: Dividir)
21. Discuta con sus compañeros de clase cómo graficaría\(f(x) = \dfrac{ax + b}{cx + d}\). ¿Qué restricciones hay que poner\(a, b, c\) y\(d\) para que la gráfica sea efectivamente una transformación de\(y = \dfrac{1}{x}\)?
22. En el Ejemplo 3.1.1 en la Sección 3.1 demostramos que no\(p(x) = \frac{4x+x^3}{x}\) es un polinomio a pesar de que su fórmula se redujo a\(4 + x^{2}\) for\(x \neq 0\). Sin embargo, es una función racional similar a las estudiadas en la sección. Con la ayuda de tus compañeros, grafica\(p(x)\).
23. Deja\(g(x) = \displaystyle \frac{x^{4} - 8x^{3} + 24x^{2} - 72x + 135}{x^{3} - 9x^{2} + 15x - 7}.\;\) Con la ayuda de tus compañeros de clase, encuentra las\(x\) - y\(y\) - intercepciones de la gráfica de\(g\). Encuentra los intervalos en los que aumenta la función, los intervalos en los que está disminuyendo y los extremos locales. Encuentra todas las asíntotas de la gráfica de\(g\) y cualquier agujero en la gráfica, si existen. Asegúrese de mostrar todo su trabajo incluyendo cualquier división polinómica o sintética. Esboce la gráfica de\(g\), usando más de una imagen si es necesario para mostrar todas las características importantes de la gráfica.

El Ejemplo 4.2.4 nos mostró que el procedimiento de seis pasos no puede decirnos todo lo importante sobre la gráfica de una función racional. Sin Cálculo, necesitamos usar nuestras calculadoras gráficas para revelar los misterios ocultos del comportamiento racional de la función. Trabajando con tus compañeros de clase, usa una calculadora gráfica para examinar las gráficas de las funciones racionales dadas en los Ejercicios 24 - 27. Compara y contrasta sus características. ¿Qué características puede revelar el proceso de seis pasos y qué características no pueden ser detectadas por él?

24. \(f(x) = \dfrac{1}{x^{2} + 1}\)
25. \(f(x) = \dfrac{x}{x^{2} + 1}\)
26. \(f(x) = \dfrac{x^{2}}{x^{2} + 1}\)
27. \(f(x) = \dfrac{x^{3}}{x^{2} + 1}\)

4.2.2 Respuestas

1. \(f(x) = \dfrac{4}{x + 2}\)
   Dominio:\((-\infty, -2) \cup (-2, \infty)\)
   No\(x\) -intercepta
   \(y\) -interceptar: asíntota\((0, 2)\)
   vertical:\(x = -2\)
   \(x \rightarrow -2^{-}, \; f(x) \rightarrow -\infty\)
   Como asíntota\(x \rightarrow -2^{+}, \; f(x) \rightarrow \infty\)
   horizontal :\(y = 0\)
   As\(x \rightarrow -\infty, \; f(x) \rightarrow 0^{-}\)
   As\(x \rightarrow \infty, \; f(x) \rightarrow 0^{+}\)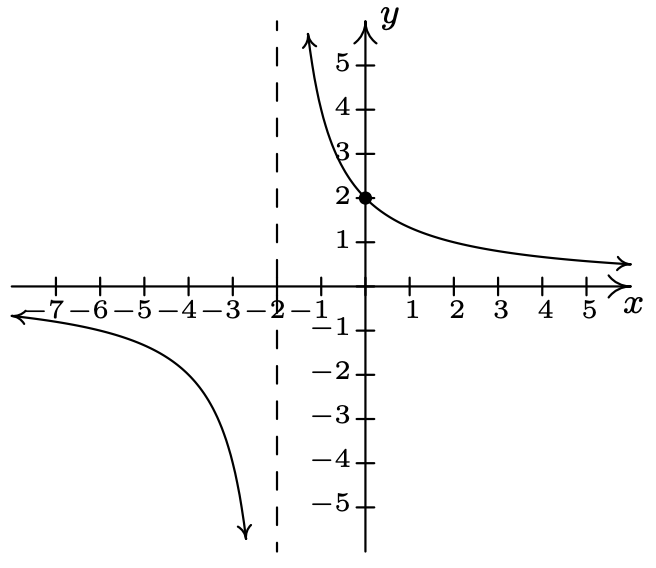

   

2. \(f(x) = \dfrac{5x}{6 - 2x}\)
   Dominio:\((-\infty, 3) \cup (3, \infty)\)
   \(x\) -intercept:\((0, 0)\)
   \(y\) -intercept: asíntota\((0, 0)\)
   vertical:\(x = 3\)
   \(x \rightarrow 3^{-}, \; f(x) \rightarrow \infty\)
   Como\(x \rightarrow 3^{+}, \; f(x) \rightarrow -\infty\)
   Horizontal asíntota:\(y = -\frac{5}{2}\)
   As\(x \rightarrow -\infty, \; f(x) \rightarrow -\frac{5}{2}^{+}\)
   As\(x \rightarrow \infty, \; f(x) \rightarrow -\frac{5}{2}^{-}\)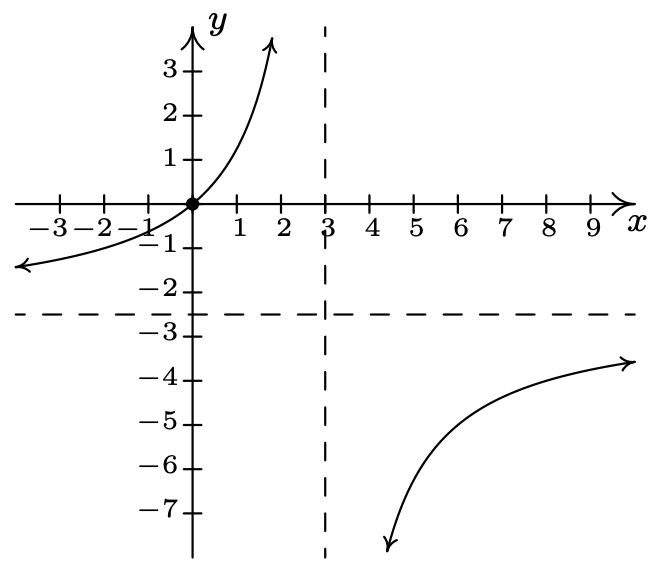

   

3. \(f(x) = \dfrac{1}{x^{2}}\)
   Dominio:\((-\infty, 0) \cup (0, \infty)\)
   No\(x\) -intercepta
   No\(y\) -intercepta Asíntota
   vertical:\(x = 0\)
   \(x \rightarrow 0^{-}, \; f(x) \rightarrow \infty\)
   Como asíntota\(x \rightarrow 0^{+}, \; f(x) \rightarrow \infty\)
   Horizontal: \(y = 0\)
   As\(x \rightarrow -\infty, \; f(x) \rightarrow 0^{+}\)
   As\(x \rightarrow \infty, \; f(x) \rightarrow 0^{+}\)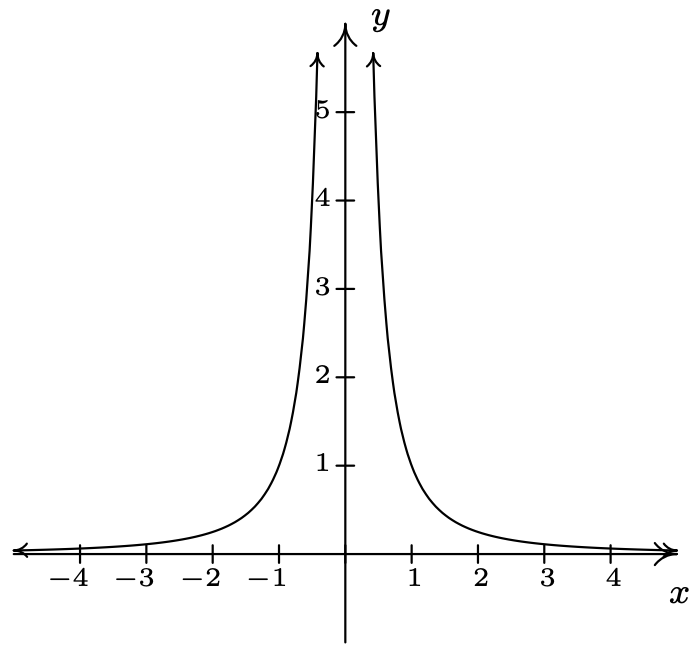

   

4. \(f(x) = \dfrac{1}{x^{2} + x - 12} = \dfrac{1}{(x - 3)(x + 4)}\)
   Dominio:\((-\infty, -4) \cup (-4, 3) \cup (3, \infty)\)
   No\(x\) -intercepta
   \(y\) -intercepción: asíntotas\((0, -\frac{1}{12})\)
   verticales:\(x = -4\) y\(x = 3\)
   \(x \rightarrow -4^{-}, \; f(x) \rightarrow \infty\)
   As\(x \rightarrow -4^{+}, \; f(x) \rightarrow -\infty\)
   As \(x \rightarrow 3^{-}, \; f(x) \rightarrow -\infty\)
   Como asíntota\(x \rightarrow 3^{+}, \; f(x) \rightarrow \infty\)
   horizontal:\(y = 0\)
   Como\(x \rightarrow -\infty, \; f(x) \rightarrow 0^{+}\)
   Como\(x \rightarrow \infty, \; f(x) \rightarrow 0^{+}\)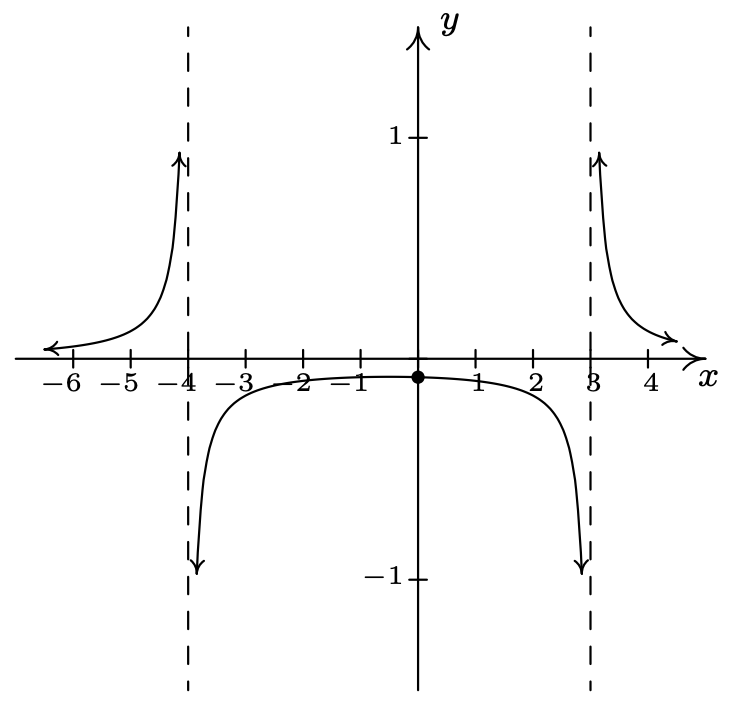

   

5. \(f(x) = \dfrac{2x - 1}{-2x^{2} - 5x + 3} = -\dfrac{2x - 1}{(2x - 1)(x + 3)}\)
   Dominio:\((-\infty, -3) \cup (-3, \frac{1}{2}) \cup (\frac{1}{2}, \infty)\)
   No\(x\) -intercepta
   \(y\) -intercepción:\((0, -\frac{1}{3})\)
   \(f(x) = \dfrac{-1}{x + 3}, \; x \neq \frac{1}{2}\)
   Agujero en la gráfica en la asíntota\((\frac{1}{2}, -\frac{2}{7})\)
   vertical:\(x = -3\)
   Como \(x \rightarrow -3^{-}, \; f(x) \rightarrow \infty\)
   Como asíntota\(x \rightarrow -3^{+}, \; f(x) \rightarrow -\infty\)
   horizontal:\(y = 0\)
   Como\(x \rightarrow -\infty, \; f(x) \rightarrow 0^{+}\)
   Como\(x \rightarrow \infty, \; f(x) \rightarrow 0^{-}\)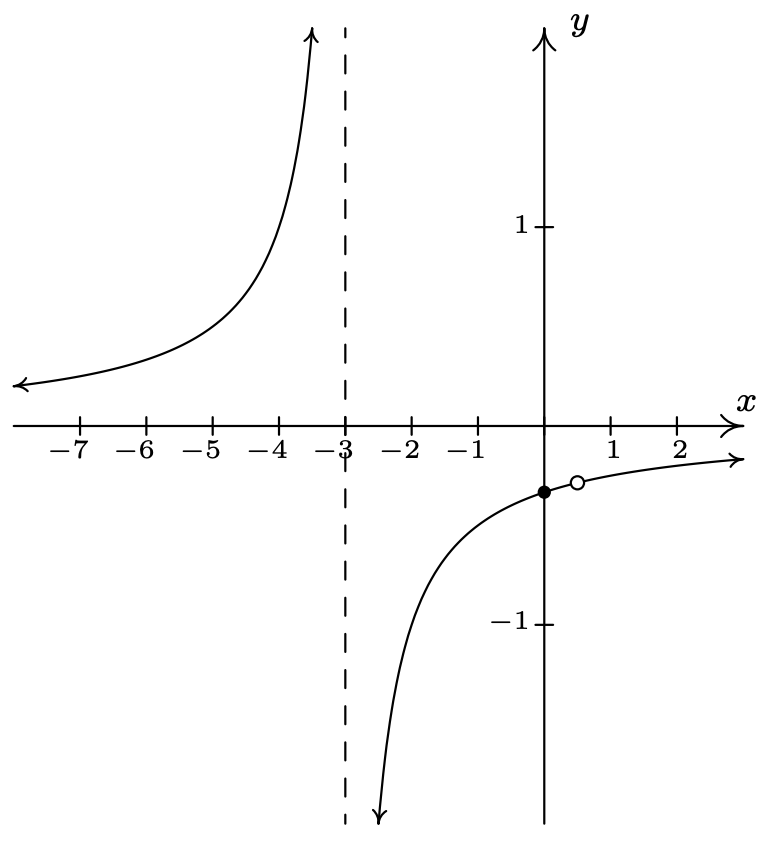

   

6. \(f(x) = \dfrac{x}{x^{2} + x - 12} = \dfrac{x}{(x - 3)(x + 4)}\)
   Dominio:\((-\infty, -4) \cup (-4, 3) \cup (3, \infty)\)
   \(x\) -interceptar:\((0, 0)\)
   \(y\) -interceptar: asíntotas\((0, 0)\)
   verticales:\(x = -4\) y\(x = 3\)
   As\(x \rightarrow -4^{-}, \; f(x) \rightarrow -\infty\)
   As\(x \rightarrow -4^{+}, \; f(x) \rightarrow \infty\)
   As\(x \rightarrow 3^{-}, \; f(x) \rightarrow -\infty\)
   As\(x \rightarrow 3^{+}, \; f(x) \rightarrow \infty\)
   Horizontal asíntota:\(y = 0\)
   As\(x \rightarrow -\infty, \; f(x) \rightarrow 0^{-}\)
   As\(x \rightarrow \infty, \; f(x) \rightarrow 0^{+}\)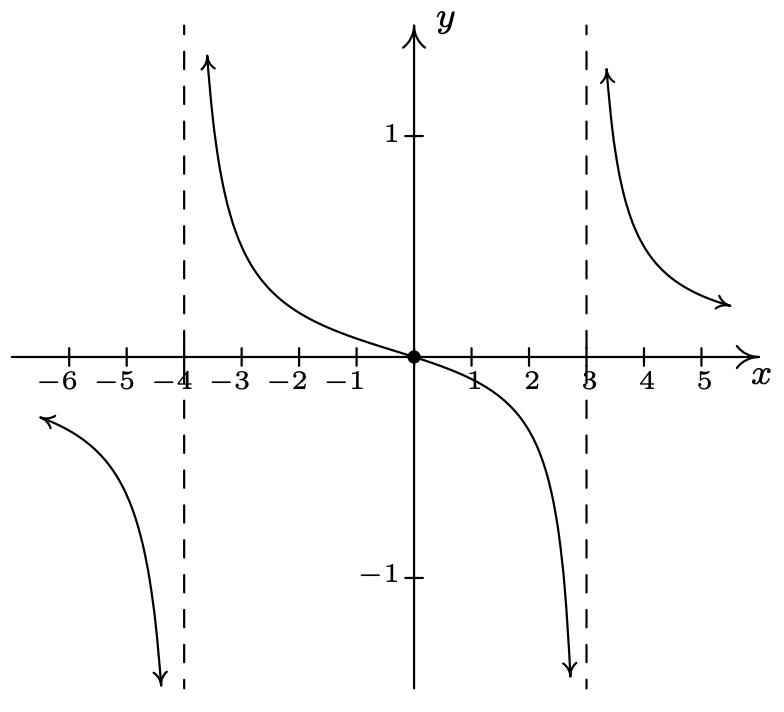

   

7. \(f(x) = \dfrac{4x}{x^{2} + 4}\)
   Dominio:\((-\infty, \infty)\)
   \(x\) -interceptar:\((0,0)\)
   \(y\) -interceptar:\((0,0)\)
   Sin asíntotas verticales
   Sin agujeros en la gráfica Asíntota
   horizontal:\(y = 0\)
   As\(x \rightarrow -\infty, f(x) \rightarrow 0^{-}\)
   As\(x \rightarrow \infty, f(x) \rightarrow 0^{+}\)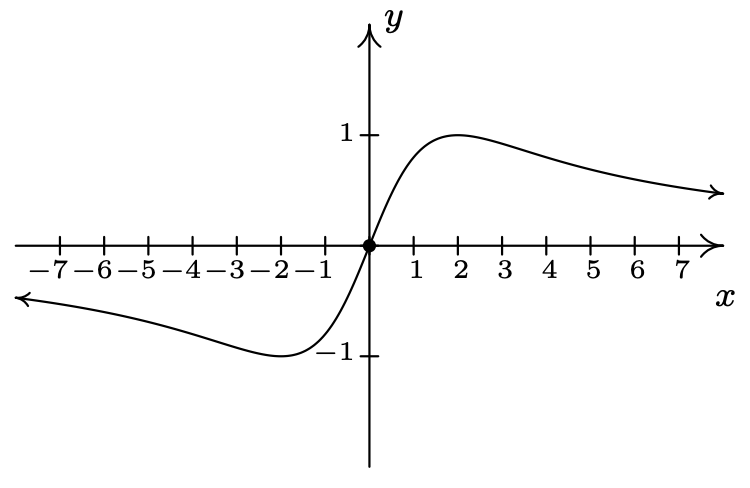

   

8. \(f(x) = \dfrac{4x}{x^{2} -4} = \dfrac{4x}{(x + 2)(x - 2)}\)
   Dominio:\((-\infty, -2) \cup (-2, 2) \cup (2, \infty)\)
   \(x\) -intercept:\((0,0)\)
   \(y\) -intercept: Asíntotas\((0,0)\)
   verticales:\(x = -2, x = 2\)
   \(x \rightarrow -2^{-}, f(x) \rightarrow -\infty\)
   As\(x \rightarrow -2^{+}, f(x) \rightarrow \infty\)
   As \(x \rightarrow 2^{-}, f(x) \rightarrow -\infty\)
   As\(x \rightarrow 2^{+}, f(x) \rightarrow \infty\)
   Sin agujeros en la gráfica Asíntota
   horizontal:\(y = 0\)
   As\(x \rightarrow -\infty, f(x) \rightarrow 0^{-}\)
   As\(x \rightarrow \infty, f(x) \rightarrow 0^{+}\)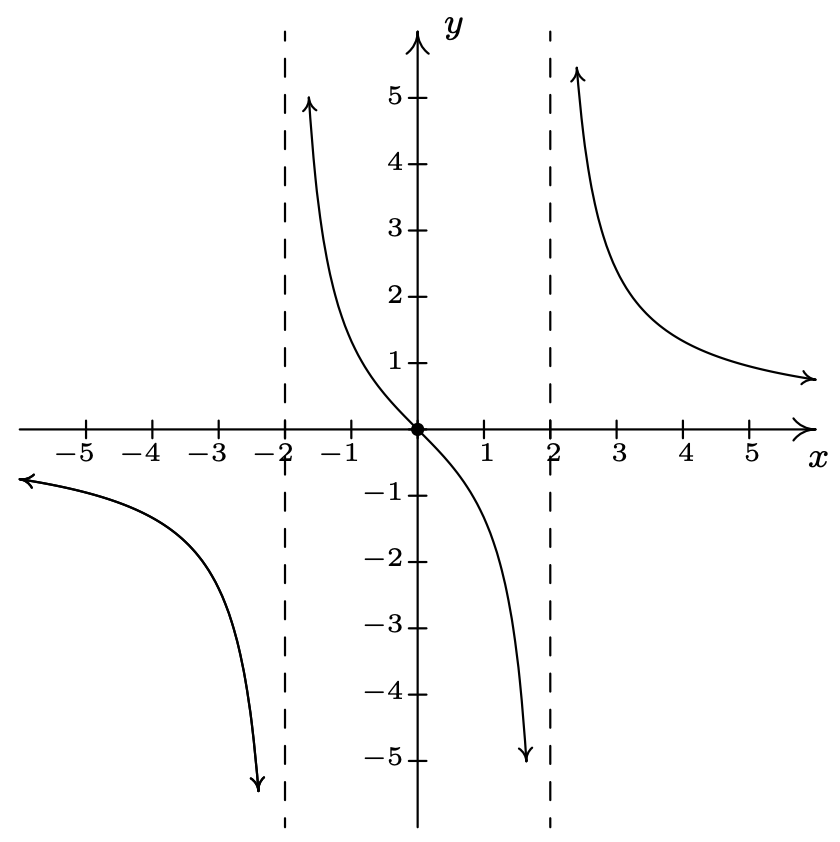

   

9. \(f(x) = \dfrac{x^2-x-12}{x^{2} +x - 6} = \dfrac{x-4}{x - 2} \, x \neq -3\)
   Dominio:\((-\infty, -3) \cup (-3, 2) \cup (2, \infty)\)
   \(x\) -intercept:\((4,0)\)
   \(y\) -intercept: Asíntota\((0,2)\)
   vertical: As\(x = 2\)
   \(x \rightarrow 2^{-}, f(x) \rightarrow \infty\)
   As\(x \rightarrow 2^{+}, f(x) \rightarrow -\infty\)
   Hole at \(\left(-3, \frac{7}{5} \right)\)
   Asíntota horizontal:\(y = 1\)
   As\(x \rightarrow -\infty, f(x) \rightarrow 1^{+}\)
   As\(x \rightarrow \infty, f(x) \rightarrow 1^{-}\)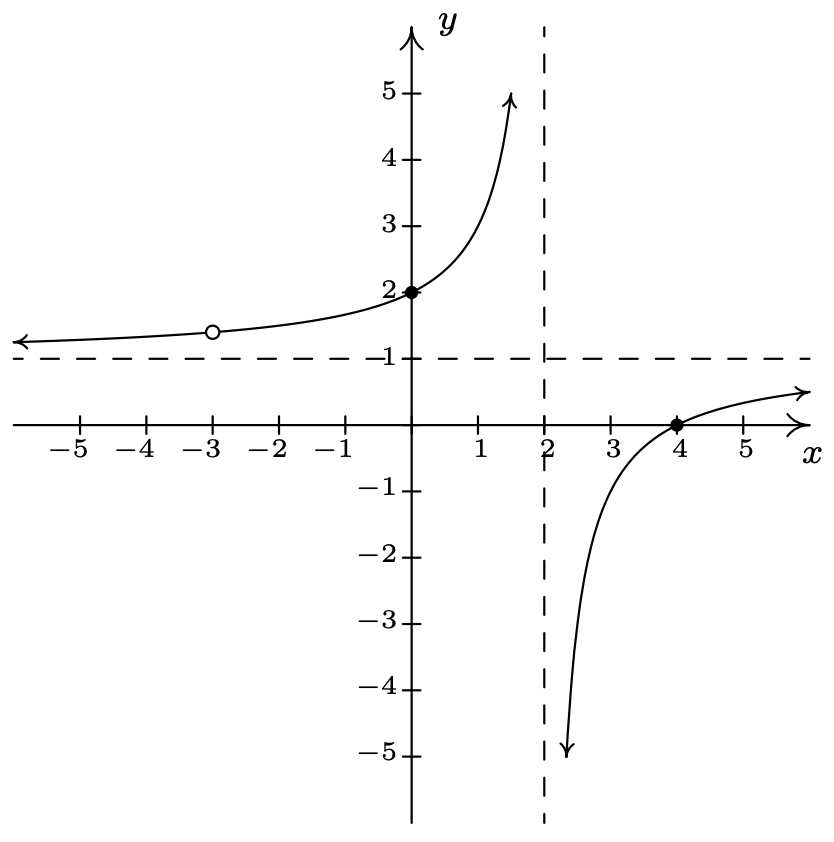

   

10. \(f(x) = \dfrac{3x^2-5x-2}{x^{2} -9} = \dfrac{(3x+1)(x-2)}{(x + 3)(x - 3)}\)
    Dominio:\((-\infty, -3) \cup (-3, 3) \cup (3, \infty)\)
    \(x\) -intercepta:\(\left(-\frac{1}{3}, 0 \right)\),\((2,0)\)
    \(y\) -interceptar: asíntotas\(\left(0, \frac{2}{9} \right)\)
    verticales:\(x = -3, x = 3\)
    Como\(x \rightarrow -3^{-}, f(x) \rightarrow \infty\)
    Como\(x \rightarrow -3^{+}, f(x) \rightarrow -\infty\)
    As\(x \rightarrow 3^{-}, f(x) \rightarrow -\infty\)
    As\(x \rightarrow 3^{+}, f(x) \rightarrow \infty\)
    Sin agujeros en la gráfica Asíntota
    horizontal:\(y = 3\)
    As\(x \rightarrow -\infty, f(x) \rightarrow 3^{+}\)
    As\(x \rightarrow \infty, f(x) \rightarrow 3^{-}\)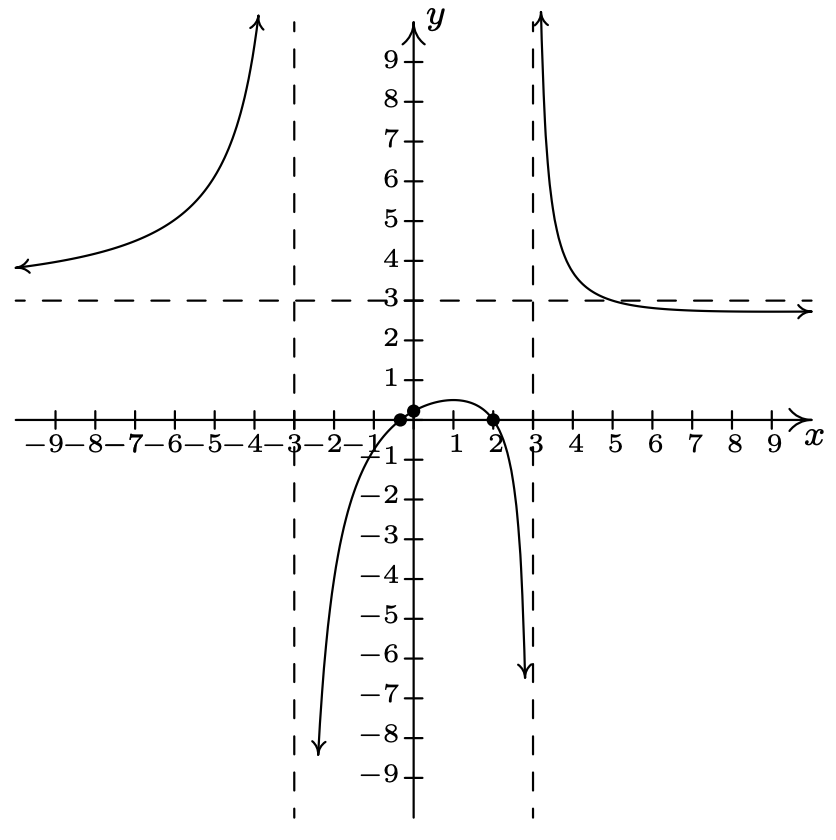

    

11. \(f(x) = \dfrac{x^2-x-6}{x+1} = \dfrac{(x-3)(x+2)}{x+1}\)
    Dominio:\((-\infty, -1) \cup (-1, \infty)\)
    \(x\) -intercepta:\((-2,0)\),\((3,0)\)
    \(y\) -interceptar: asíntota\((0,-6)\)
    vertical:\(x = -1\)
    \(x \rightarrow -1^{-}, f(x) \rightarrow \infty\)
    Como\(x \rightarrow -1^{+}, f(x) \rightarrow -\infty\)
    Asíntota inclinada:\(y = x-2\)
    As\(x \rightarrow -\infty\), la gráfica está arriba\(y=x-2\)
    As\(x \rightarrow \infty\), la gráfica está abajo\(y=x-2\)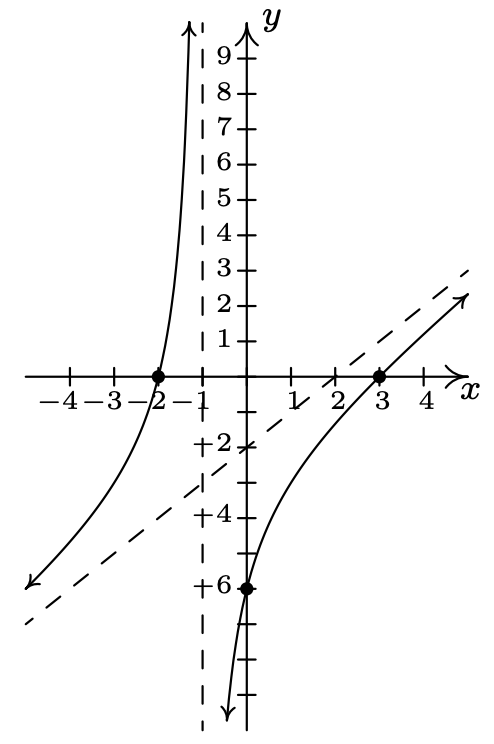

    

12. \(f(x) = \dfrac{x^2-x}{3-x} = \dfrac{x(x-1)}{3-x}\)
    Dominio:\((-\infty, 3) \cup (3, \infty)\)
    \(x\) -intercepta:\((0,0)\),\((1,0)\)
    \(y\) -interceptar: asíntota\((0,0)\)
    vertical:\(x = 3\)
    \(x \rightarrow 3^{-}, f(x) \rightarrow \infty\)
    Como\(x \rightarrow 3^{+}, f(x) \rightarrow -\infty\)
    Asíntota inclinada:\(y = -x-2\)
    As\(x \rightarrow -\infty\), la gráfica está arriba\(y=-x-2\)
    As\(x \rightarrow \infty\), la gráfica está abajo\(y=-x-2\)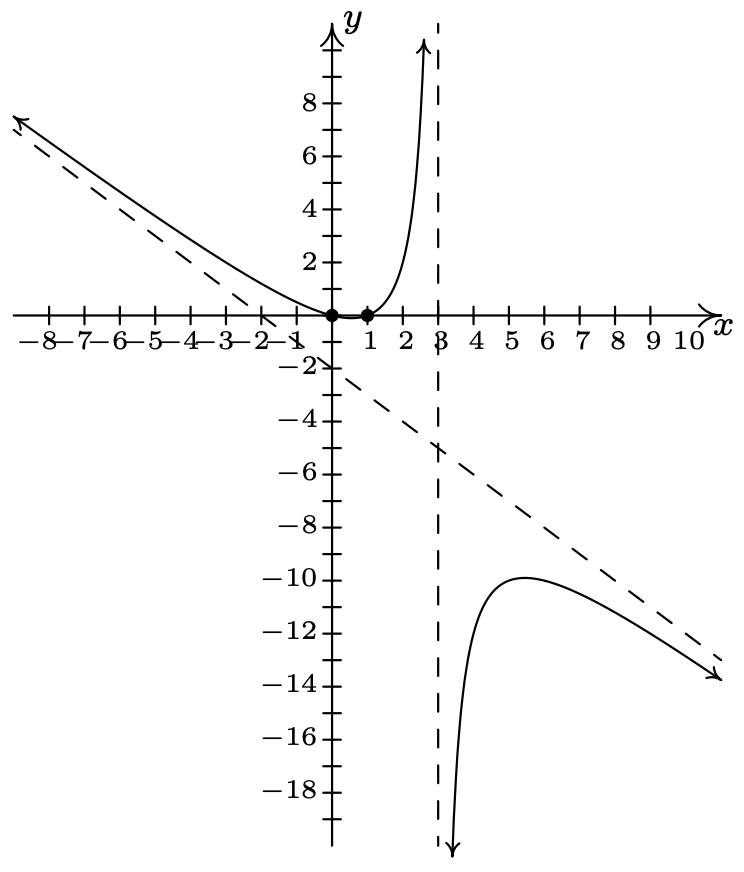

    

13. \(f(x) = \dfrac{x^3+2x^2+x}{x^{2} -x-2} = \dfrac{x(x+1)}{x - 2} \, x \neq -1\)
    Dominio:\((-\infty, -1) \cup (-1, 2) \cup (2, \infty)\)
    \(x\) -intercept:\((0,0)\)
    \(y\) -intercept: asíntota\((0,0)\)
    vertical: As\(x = 2\)
    \(x \rightarrow 2^{-}, f(x) \rightarrow -\infty\)
    As\(x \rightarrow 2^{+}, f(x) \rightarrow \infty\)
    Hole at \((-1,0)\)
    Asíntota inclinada:\(y = x+3\)
    As\(x \rightarrow -\infty\), la gráfica está debajo\(y=x+3\)
    As\(x \rightarrow \infty\), la gráfica está arriba\(y=x+3\)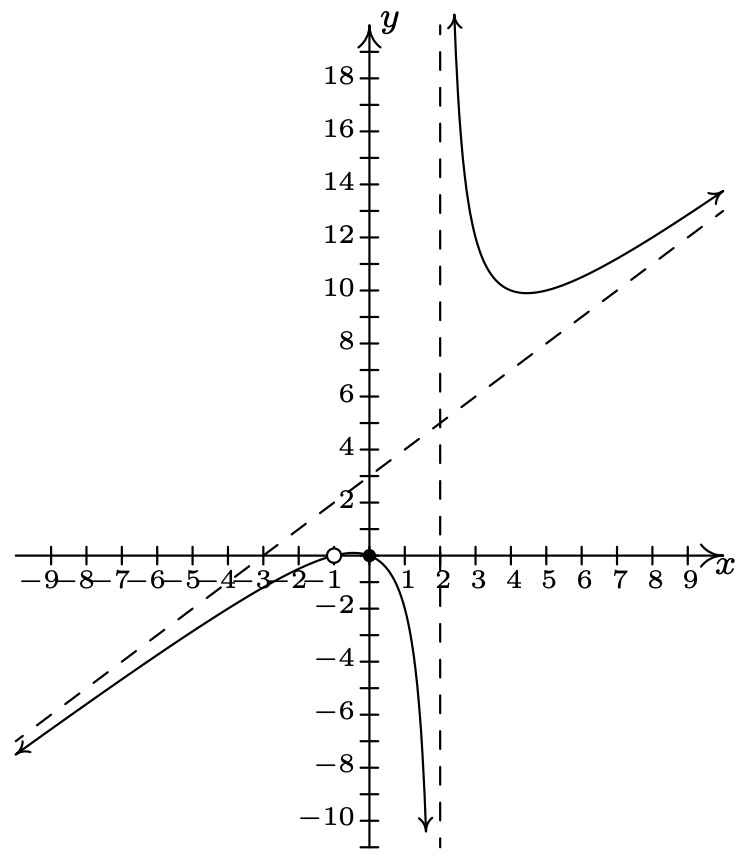

    

14. \(f(x) = \dfrac{-x^{3} + 4x}{x^{2} - 9}\)
    Dominio:\((-\infty, -3) \cup (-3, 3) \cup (3, \infty)\)
    \(x\) -intercepta:\((-2, 0), (0, 0), (2, 0)\)
    \(y\) -interceptar: asíntotas\((0, 0)\)
    verticales:\(x = -3, x = 3\)
    \(x \rightarrow -3^{-}, \; f(x) \rightarrow \infty\)
    As\(x \rightarrow -3^{+}, \; f(x) \rightarrow -\infty\)
    As \(x \rightarrow 3^{-}, \; f(x) \rightarrow \infty\)
    Como asíntota\(x \rightarrow 3^{+}, \; f(x) \rightarrow -\infty\)
    inclinada:\(y = -x\)
    As\(x \rightarrow -\infty\), la gráfica está arriba\(y=-x\)
    As\(x \rightarrow \infty\), la gráfica está abajo\(y=-x\)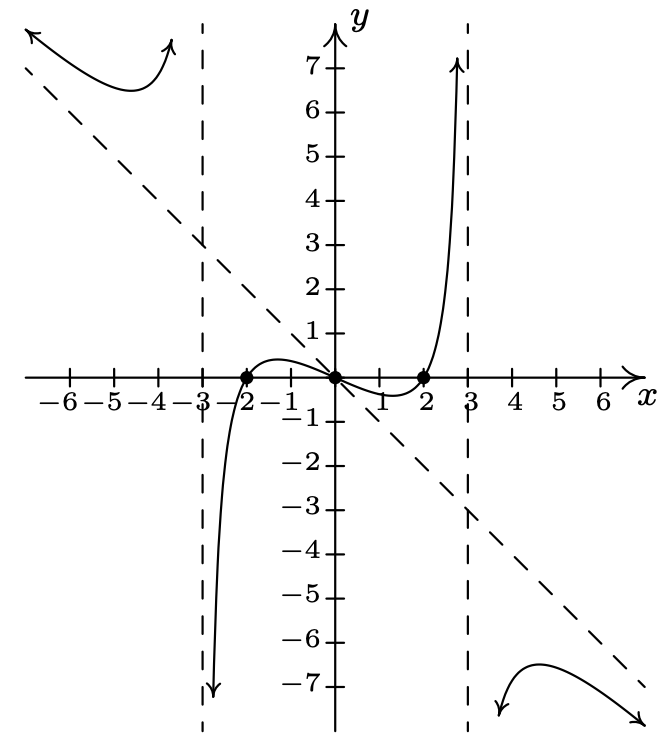

    

15. \(f(x) = \dfrac{x^3-2x^2+3x}{2x^2+2}\)
    Dominio:\((-\infty,\infty)\)
    \(x\) -interceptar:\((0,0)\)
    \(y\) -interceptar: asíntota\((0,0)\)
    inclinada:\(y = \frac{1}{2}x-1\)
    As\(x \rightarrow -\infty\), la gráfica está abajo\(y = \frac{1}{2}x-1\)
    As\(x \rightarrow \infty\), la gráfica está arriba\(y = \frac{1}{2}x-1\)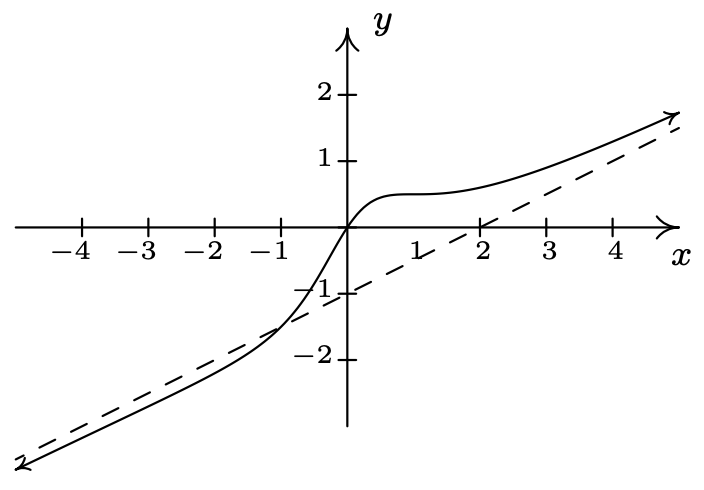

    

16. \(f(x) = \dfrac{x^{2} - 2x + 1}{x^{3} + x^{2} - 2x}\)
    Dominio:\((-\infty, -2) \cup (-2, 0) \cup (0, 1) \cup (1, \infty)\)
    \(f(x) = \dfrac{x - 1}{x(x + 2)}, \; x \neq 1\)
    No\(x\) -intercepta
    No\(y\) -intercepta asíntotas
    verticales:\(x = -2\) y\(x = 0\)
    As\(x \rightarrow -2^{-}, \; f(x) \rightarrow -\infty\)
    As\(x \rightarrow -2^{+}, \; f(x) \rightarrow \infty\)
    \(x \rightarrow 0^{-}, \; f(x) \rightarrow \infty\)
    Como\(x \rightarrow 0^{+}, \; f(x) \rightarrow -\infty\)
    Agujero en la gráfica en la asíntota\((1, 0)\)
    Horizontal:\(y = 0\)
    Como\(x \rightarrow -\infty, \; f(x) \rightarrow 0^{-}\)
    Como\(x \rightarrow \infty, \; f(x) \rightarrow 0^{+}\)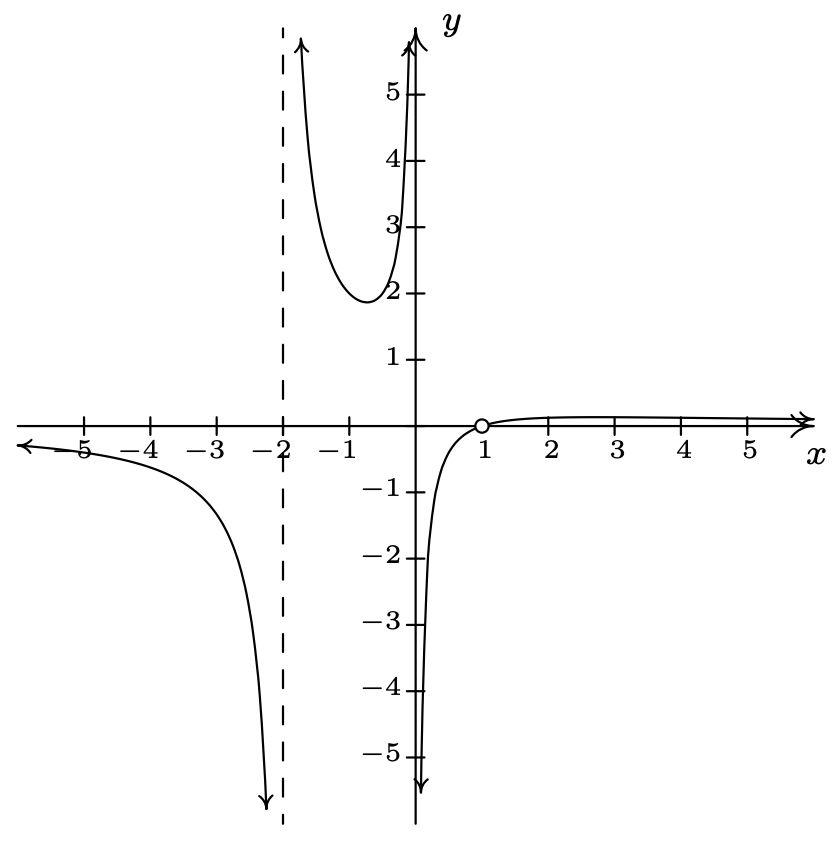

    

17. \(f(x) = \dfrac{1}{x - 2}\)
    Desplazar la gráfica de\(y = \dfrac{1}{x}\)
    a la derecha 2 unidades.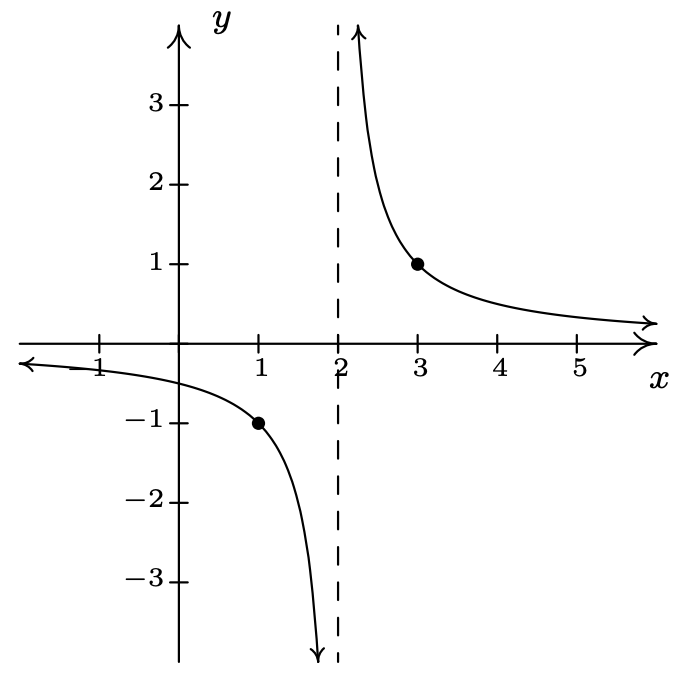

    

18. \(g(x) = 1 - \dfrac{3}{x}\)
    Estirar verticalmente la gráfica de\(y = \dfrac{1}{x}\)
    por un factor de 3.
    Refleja la gráfica de\(y = \dfrac{3}{x}\)
    alrededor del\(x\) eje.
    Desplazar la gráfica de 1 unidad\(y = -\dfrac{3}{x}\)
    hacia arriba.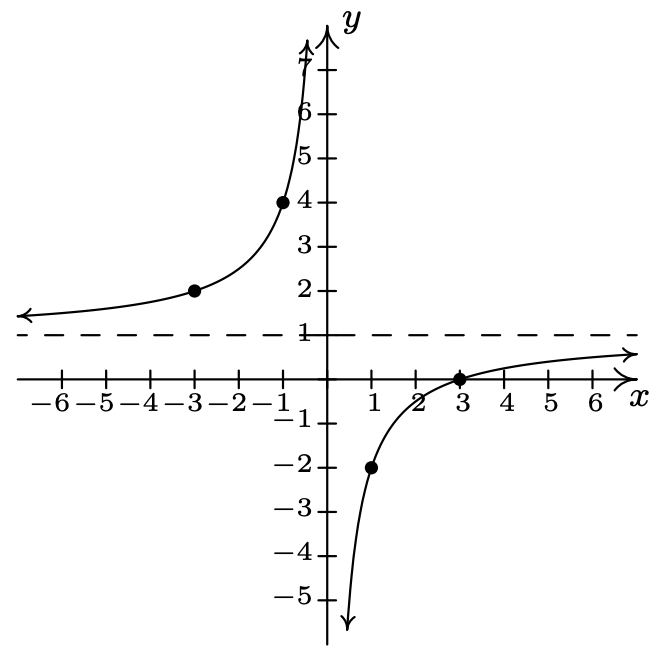

    

19. \(h(x) = \dfrac{-2x + 1}{x} = -2 + \dfrac{1}{x}\)
    Desplazar la gráfica de\(y = \dfrac{1}{x}\)
    abajo 2 unidades.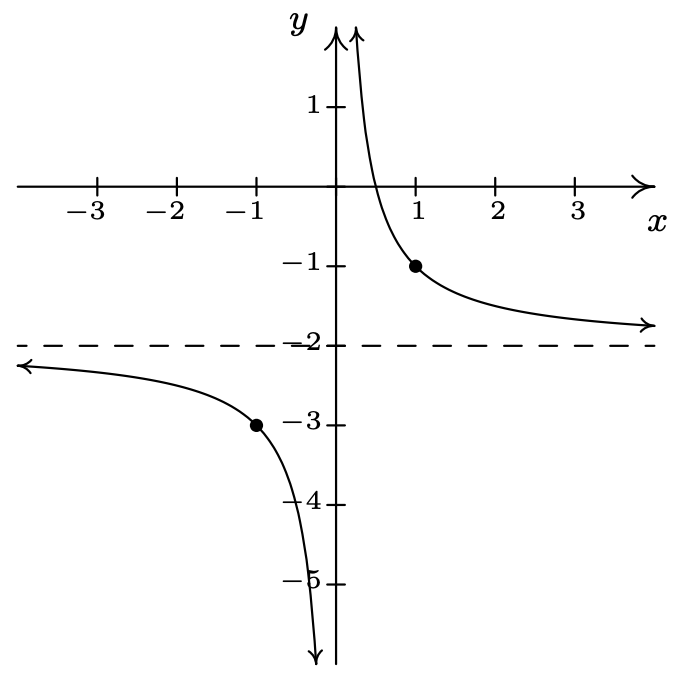

    

20. \(j(x) = \dfrac{3x - 7}{x - 2} = 3 - \dfrac{1}{x - 2}\)
    Desplazar la gráfica de\(y = \dfrac{1}{x}\)
    a la derecha 2 unidades.
    Refleja la gráfica de\(y = \dfrac{1}{x - 2}\)
    alrededor del\(x\) eje.
    Desplazar la gráfica de\(y = -\dfrac{1}{x - 2}\)
    hasta 3 unidades.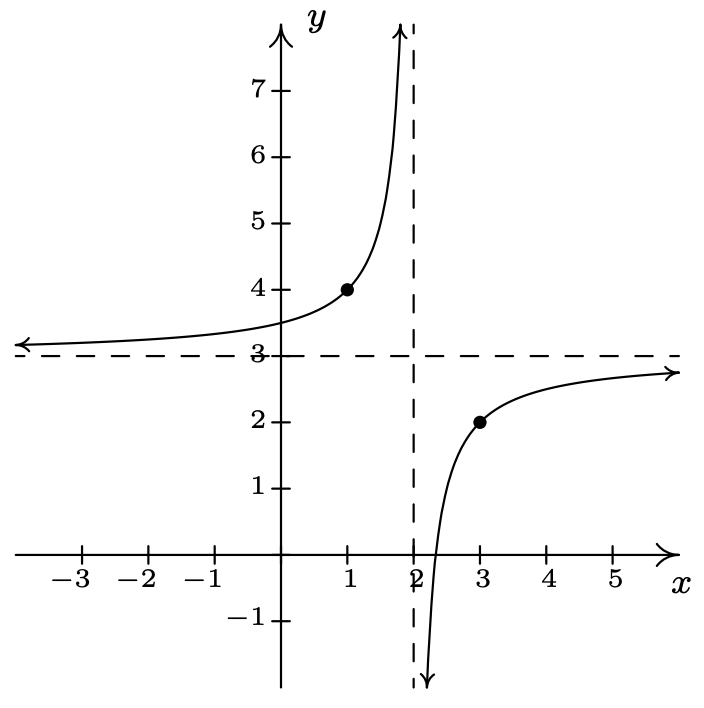

    

---

Referencia

¹ Recordemos que, para nuestros fines, esto significa que las gráficas están desprovistas de saltos, saltos o agujeros

² Otro resultado de Cálculo.

³ Como mencionamos al menos una vez antes, ya que las funciones pueden tener como máximo una\(y\) -intercepción, una vez que encontramos que (0, 0) está en la gráfica, sabemos que es la\(y\) -intercepción.

⁴ El diagrama de señales en el paso 6 también determinará el comportamiento cerca de las asíntotas verticales.

⁵ El valor real de venta al por menor\(f(−2.000001)\) es de aproximadamente −1,500,000.

⁶ Hemos dejado deliberadamente las etiquetas en el eje y porque conocemos solo el comportamiento cercano\(x = ±2\), no los valores reales de la función.

⁷ Al igual que con las asíntotas verticales en el paso anterior, solo conocemos el comportamiento de la gráfica como\(x \rightarrow \pm \infty\). Por esa razón, no proporcionamos etiquetas\(x\) de eje.

⁸ En este caso particular, podemos evitar los valores de prueba, ya que nuestro análisis del comportamiento de\(f\) cerca de las asíntotas verticales y nuestro análisis final de comportamiento nos han dado los signos en cada uno de los intervalos de prueba. En general, sin embargo, esto no siempre será así, por lo que para fines de demostración, continuamos con nuestra construcción habitual.

⁹ Y Jeff no piensa mucho en ello para empezar...

¹⁰ ¡Por eso lo llamamos MYT!

¹¹ Es decir, si usas una calculadora para graficar. Una vez más, Calculus es la herramienta eléctrica de gráficos definitiva.

¹² En el denominador, tendríamos\((\text { billion })^{2}-1 \text { billion }-6\). Es fácil ver por qué el 6 es insignificante, pero ignorar los mil millones parece criminal. Sin embargo, en comparación con\((1 \text { billion })^{2}\), está en el lado insignificante; es 10 ¹⁸ versus 10 ⁹. Estamos nuevamente utilizando el hecho de que para los polinomios, el comportamiento final está determinado por el término principal, por lo que en el denominador, el\(x^{2}\) término gana sobre el\(x\) término.

¹³ ¡Apuesto a que nunca pensaste que nunca volverías a ver esas cosas antes del examen final!

¹⁴ Pero ten la seguridad, ¡algunas gráficas sí!

¹⁵ ¡Esto no nos impedirá darle el viejo intento de colegio comunitario, sin embargo!

¹⁶ ¡Así que hasta Jeff en este punto puede comprobar si hay simetría! Dejamos que el lector muestre que\(r(−x) = r(x)\) así\(r\) es parejo, y, de ahí, su gráfica es simétrica alrededor del\(y\) eje -eje.

¹⁷ Sin apelar al Cálculo, claro.

¹⁸ Una vez que hayas realizado el procedimiento de seis pasos, usa tu calculadora para graficar esta función en la ventana de visualización [0, 12] × [0, 0.25]. ¿Qué ves?