1.1: Revisión de Funciones
- Page ID
- 116826
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Utilice notación funcional para evaluar una función.
- Determinar el dominio y el rango de una función.
- Dibuja la gráfica de una función.
- Encuentra los ceros de una función.
- Reconocer una función a partir de una tabla de valores.
- Hacer nuevas funciones a partir de dos o más funciones dadas.
- Describir las propiedades de simetría de una función.
En esta sección, proporcionamos una definición formal de una función y examinamos varias formas en que se representan las funciones, a saber, a través de tablas, fórmulas y gráficos. Estudiamos la notación formal y los términos relacionados con las funciones. También definimos composición de funciones y propiedades de simetría. La mayor parte de este material será una revisión para ti, pero sirve como una referencia útil para recordarte algunas de las técnicas algebraicas útiles para trabajar con funciones.
Funciones
Dados dos conjuntos\(A\) y\(B\) un conjunto con elementos que son pares ordenados\((x,y)\) donde\(x\) es un elemento de\(A\) y\(y\) es un elemento de\(B,\) es una relación de\(A\) a\(B\). Una relación de\(A\) a\(B\) define una relación entre esos dos conjuntos. Una función es un tipo especial de relación en la que cada elemento del primer conjunto está relacionado exactamente con un elemento del segundo conjunto. El elemento del primer conjunto se llama entrada; el elemento del segundo conjunto se llama salida. Las funciones se utilizan todo el tiempo en matemáticas para describir las relaciones entre dos conjuntos. Para cualquier función, cuando conocemos la entrada, se determina la salida, por lo que decimos que la salida es una función de la entrada. Por ejemplo, el área de un cuadrado está determinada por su longitud lateral, por lo que decimos que el área (la salida) es una función de su longitud lateral (la entrada). La velocidad de una pelota lanzada al aire se puede describir como una función de la cantidad de tiempo que la pelota está en el aire. El costo de enviar un paquete es una función del peso del paquete. Dado que las funciones tienen tantos usos, es importante tener definiciones precisas y terminología para estudiarlas.

Una función\(f\) consiste en un conjunto de entradas, un conjunto de salidas y una regla para asignar cada entrada a exactamente una salida. El conjunto de entradas se llama el dominio de la función. El conjunto de salidas se llama el rango de la función.
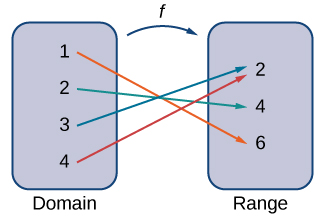
Por ejemplo, considere la función\(f\), donde el dominio es el conjunto de todos los números reales y la regla es cuadrar la entrada. Después, la entrada\(x=3\) se asigna a la salida\(3^2=9\).
Dado que cada número real no negativo tiene una raíz cuadrada de valor real, cada número no negativo es un elemento del rango de esta función. Dado que no hay un número real con un cuadrado que sea negativo, los números reales negativos no son elementos del rango. Concluimos que el rango es el conjunto de números reales no negativos.
Para una función general\(f\) con dominio\(D\), a menudo usamos\(x\) para denotar la entrada y\(y\) para denotar la salida asociada con\(x\). Al hacerlo, nos referimos\(x\) como la variable independiente y\(y\) como la variable dependiente, porque depende de ella\(x\). Usando la notación de funciones, escribimos\(y=f(x)\), y leemos esta ecuación como “\(y\)es igual a\(x.”\) Para la función\(f\) de cuadratura descrita anteriormente, escribimos\(f(x)=x^2\).
El concepto de una función se puede visualizar utilizando Figuras\(\PageIndex{1}\) -\(\PageIndex{3}\).
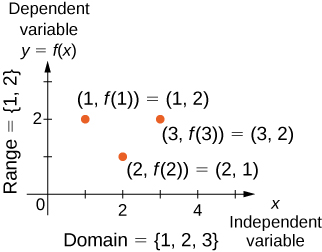
También podemos visualizar una función trazando puntos\((x,y)\) en el plano de coordenadas donde\(y=f(x)\). La gráfica de una función es el conjunto de todos estos puntos. Por ejemplo, considere la función\(f\), donde el dominio es el conjunto\(D=\{1,2,3\}\) y la regla es\(f(x)=3−x\). En la Figura\(\PageIndex{4}\), trazamos una gráfica de esta función.
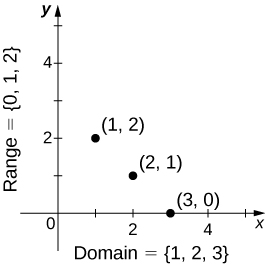
Cada función tiene un dominio. Sin embargo, a veces una función es descrita por una ecuación, como en\(f(x)=x^2\), sin dominio específico dado. En este caso, el dominio se toma como el conjunto de todos los números reales\(x\) para lo cual\(f(x)\) es un número real. Por ejemplo, dado que cualquier número real puede ser cuadrado, si no se especifica ningún otro dominio, consideramos que el dominio de\(f(x)=x^2\) es el conjunto de todos los números reales. Por otro lado, la función raíz cuadrada\(f(x)=\sqrt{x}\) sólo da una salida real si no\(x\) es negativa. Por lo tanto, el dominio de la función\(f(x)=\sqrt{x}\) es el conjunto de números reales no negativos, a veces llamado dominio natural.
Para las funciones\(f(x)=x^2\) y\(f(x)=\sqrt{x}\), los dominios son conjuntos con un número infinito de elementos. Claramente no podemos enumerar todos estos elementos. Al describir un conjunto con un número infinito de elementos, a menudo es útil usar setbuilder o notación de intervalo. Cuando se usa la notación set-builder para describir un subconjunto de todos los números reales, denotados\(R\), escribimos
\[\{x\,|\,\textit{x has some property}\}. \nonumber \]
Leemos esto como el conjunto de números reales\(x\) tal que\(x\) tiene alguna propiedad. Por ejemplo, si nos interesara el conjunto de números reales que son mayores que uno pero menores que cinco, podríamos denotar este conjunto usando notación set-builder escribiendo
\[\{x\,|\,1<x<5\}.\nonumber \]
Un conjunto como este, que contiene todos los números mayores que\(a\) y menores que también se\(b,\) puede denotar usando la notación de intervalo\((a,b)\). Por lo tanto,
\[(1,5)=\{x\,|\,1<x<5\}.\nonumber \]
Los números\(1\) y\(5\) se llaman los puntos finales de este conjunto. Si queremos considerar el conjunto que incluye los endpoints, denotaríamos este conjunto escribiendo
\[[1,5]=\{x\,|\,1 \le x \le 5\}.\nonumber \]
Podemos usar notación similar si queremos incluir uno de los puntos finales, pero no el otro. Para denotar el conjunto de números reales no negativos, usaríamos la notación set-builder
\[\{x\,|\,x\ge 0\}.\nonumber \]
El número más pequeño en este conjunto es cero, pero este conjunto no tiene un número mayor. Usando la notación de intervalos, usaríamos el símbolo\(∞,\) que se refiere al infinito positivo, y escribiríamos el conjunto como
\[[0,∞)=\{x\,|\,x\ge 0\}.\nonumber \]
Es importante señalar que no\(∞\) es un número real. Aquí se usa simbólicamente para indicar que este conjunto incluye todos los números reales mayores o iguales a cero. Del mismo modo, si quisiéramos describir el conjunto de todos los números no positivos, podríamos escribir
\[(−∞,0]=\{x\,|\,x≤0\}.\nonumber \]
Aquí, la notación\(−∞\) se refiere al infinito negativo, e indica que estamos incluyendo todos los números menores o iguales a cero, por pequeños que sean. El conjunto
\[(−∞,∞)=\{\textit{x} \,|\, \textit{x is any real number}\}\nonumber \]
se refiere al conjunto de todos los números reales. Algunas funciones se definen usando diferentes ecuaciones para diferentes partes de su dominio. Este tipo de funciones se conocen como funciones definidas por partes. Por ejemplo, supongamos que queremos definir una función\(f\) con un dominio que sea el conjunto de todos los números reales tales que\(f(x)=3x+1\) para\(x≥2\) y\(f(x)=x^2\) para\( x<2\). Denotamos esta función escribiendo
\[f(x)=\begin{cases} 3x+1, & \text{if } x≥2 \\ x^2, & \text{if } x<2 \end{cases}\nonumber \]
Al evaluar esta función para una entrada\(x\), la ecuación a utilizar depende de si\(x≥2\) o\(x<2\). Por ejemplo, ya que\(5>2\), utilizamos el hecho de que\(f(x)=3x+1\) para\(x≥2\) y vemos eso\(f(5)=3(5)+1=16\). Por otro lado, para\(x=−1\), utilizamos el hecho de que\(f(x)=x^2\) para\(x<2\) y ver eso\(f(−1)=1\).
Para la función\(f(x)=3x^2+2x−1\), evalúe:
- \(f(−2)\)
- \(f(\sqrt{2})\)
- \(f(a+h)\)
Solución
Sustituir el valor dado por\(x\) en la fórmula por\(f(x)\).
- \(f(−2)=3(−2)^2+2(−2)−1=12−4−1=7\)
- \(f(\sqrt{2})=3(\sqrt{2})^2+2\sqrt{2}−1=6+2\sqrt{2}−1=5+2\sqrt{2}\)
- \(f(a+h)=3(a+h)^2+2(a+h)−1=3(a^2+2ah+h^2)+2a+2h−1=3a^2+6ah+3h^2+2a+2h−1\)
Para\(f(x)=x^2−3x+5\), evaluar\(f(1)\) y\(f(a+h)\).
- Pista
-
Sustituto\(1\) y\(a+h\) para\(x\) en la fórmula para\(f(x)\).
- Responder
-
\(f(1)=3 \)y\(f(a+h)=a^2+2ah+h^2−3a−3h+5\)
Para cada una de las siguientes funciones, determinar el dominio i. y el rango ii.
- \(f(x)=(x−4)^2+5\)
- \(f(x)=\sqrt{3x+2}−1\)
- \(f(x)=\dfrac{3}{x−2}\)
Solución
a. Considerar\(f(x)=(x−4)^2+5.\)
1.Dado que\(f(x)=(x−4)^2+5\) es un número real para cualquier número real\(x\), el dominio de\(f\) es el intervalo\((−∞,∞)\).
2. Ya que\((x−4)^2≥0\), sabemos\(f(x)=(x−4)^2+5≥5\). Por lo tanto, el rango debe ser un subconjunto de\(\{y\,|\,y≥5\}.\) Para mostrar que cada elemento de este conjunto está en el rango, necesitamos mostrar que para un dado\(y\) en ese conjunto, hay un número real\(x\) tal que\(f(x)=(x−4)^2+5=y\). Resolviendo esta ecuación para\(x,\) vemos que necesitamos\(x\) tal que
\((x−4)^2=y−5.\)
Esta ecuación se satisface siempre y cuando exista un número real\(x\) tal que
\(x−4=±\sqrt{y−5}\)
Ya que\(y≥5\), la raíz cuadrada está bien definida. Concluimos que para\(x=4±\sqrt{y−5},\)\(f(x)=y,\) y por lo tanto el rango es\(\{y\,|\,y≥5 \}.\)
b. Considerar\(f(x)=\sqrt{3x+2}−1\).
1.Para encontrar el dominio de\(f\), necesitamos la expresión\(3x+2≥0\). Resolviendo esta desigualdad, concluimos que el dominio es\(\{x\,|\,x≥−2/3\}.\)
2.Para encontrar la gama de\(f\), observamos que desde\(\sqrt{3x+2}≥0,\)\(f(x)=\sqrt{3x+2}−1≥−1\). Por lo tanto, el rango de\(f\) debe ser un subconjunto del conjunto\(\{y\,|\,y≥−1\}\). Para demostrar que cada elemento de este conjunto está en el rango de\(f\), necesitamos mostrar que para todos\(y\) en este conjunto, existe un número real\(x\) en el dominio tal que\(f(x)=y.\) Let\(y≥−1.\) Then,\(f(x)=y\) if and only if
\(\sqrt{3x+2}−1=y.\)
Resolviendo esta ecuación para que\(x,\) veamos que\(x\) hay que resolver la ecuación
\(\sqrt{3x+2}=y+1.\)
Ya que\(y≥−1\), tal\(x\) podría existir. Al cuadrar ambos lados de esta ecuación, tenemos\(3x+2=(y+1)^2.\)
Por lo tanto, necesitamos
\(3x=(y+1)^2−2,\)
lo que implica
\(x=\frac{1}{3}(y+1)^2−\frac{2}{3}.\)
Sólo tenemos que verificar que\(x\) esté en el dominio de\(f\). Dado que el dominio de\(f\) consiste en todos los números reales mayores o iguales a\(\frac{−2}{3}\), y
\(\frac{1}{3}(y+1)^2-\frac{2}{3}≥−\frac{2}{3},\)
existe un\(x\) en el dominio de\(f\). Concluimos que el rango de\(f\) es\(\{y\,|\,y≥−1\}.\)
c. Considerar\(f(x)=\dfrac{3}{x−2}.\)
1.Dado que\(3/(x−2)\) se define cuando el denominador es distinto de cero, el dominio es\(\{x\,|\,x≠2\}.\)
2.Para encontrar el rango de\(f,\) necesitamos encontrar los valores de\(y\) tal que exista un número real\(x\) en el dominio con la propiedad que
\(\dfrac{3}{x−2}=y.\)
Resolviendo esta ecuación para\(x,\) encontramos que
\(x=\dfrac{3}{y}+2.\)
Por lo tanto, siempre y cuando\(y≠0\), exista un número real\(x\) en el dominio tal que\(f(x)=y\). Así, el rango es\(\{y\,|\,y≠0\}.\)
Encuentre el dominio y la gama para\(f(x)=\sqrt{4−2x}+5.\)
- Pista
-
Uso\(4−2x≥0\).
- Responder
-
Dominio =\(\{x\,|\,x≤2\}\) y rango =\(\{y\,|\,y≥5\}\)
Representando funciones
Normalmente, una función se representa usando una o más de las siguientes herramientas:
- Una mesa
- Un gráfico
- Una fórmula
Podemos identificar una función en cada forma, pero también podemos utilizarlas juntas. Por ejemplo, podemos trazar en una gráfica los valores de una tabla o crear una tabla a partir de una fórmula.
Mesas
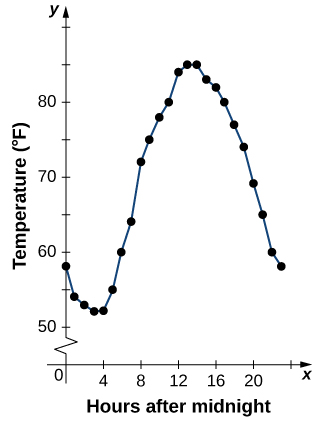
Las funciones descritas usando una tabla de valores surgen frecuentemente en aplicaciones del mundo real. Considera el siguiente ejemplo sencillo. Podemos describir la temperatura en un día determinado como una función de la hora del día. Supongamos que registramos la temperatura cada hora durante un periodo de 24 horas a partir de la medianoche. Dejamos que nuestra variable de entrada\(x\) sea el tiempo después de la medianoche, medida en horas, y la variable de salida\(y\) sea la temperatura\(x\) horas después de la medianoche, medida en grados Fahrenheit. Registramos nuestros datos en Tabla\(\PageIndex{1}\).
| Hora Después de Medianoche | Temperatura (°F) | Hora Después de Medianoche | Temperatura (°F) |
|---|---|---|---|
| 0 | 58 | 12 | 84 |
| 1 | 54 | 13 | 85 |
| 2 | 53 | 14 | 85 |
| 3 | 52 | 15 | 83 |
| 4 | 52 | 16 | 82 |
| 5 | 55 | 17 | 80 |
| 6 | 60 | 18 | 77 |
| 7 | 64 | 19 | 74 |
| 8 | 72 | 20 | 69 |
| 9 | 75 | 21 | 65 |
| 10 | 78 | 22 | 60 |
| 11 | 80 | 23 | 58 |
Podemos ver en la tabla que la temperatura es función del tiempo, y la temperatura disminuye, luego aumenta, y luego vuelve a disminuir. Sin embargo, no podemos obtener una imagen clara del comportamiento de la función sin graficarla.
Gráficas
Dada una función\(f\) descrita por una tabla, podemos proporcionar una imagen visual de la función en forma de gráfica. Graficar las temperaturas listadas en la Tabla\(\PageIndex{1}\) puede darnos una mejor idea de su fluctuación a lo largo del día. La figura\(\PageIndex{5}\) muestra la gráfica de la función de temperatura.
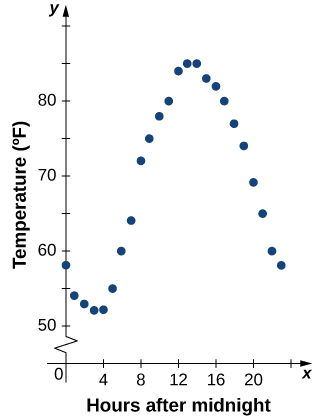
A partir de los puntos trazados en la gráfica de la Figura\(\PageIndex{5}\), podemos visualizar la forma general de la gráfica. A menudo es útil conectar los puntos en la gráfica, que representan los datos de la tabla. En este ejemplo, aunque no podemos llegar a ninguna conclusión definitiva respecto a cuál era la temperatura en ningún momento para el que no se registró la temperatura, dado el número de puntos de datos recogidos y el patrón en estos puntos, es razonable sospechar que las temperaturas en otros momentos siguieron un patrón similar, como podemos ver en la Figura\(\PageIndex{6}\).
Fórmulas algebraicas
A veces no se nos dan los valores de una función en forma de tabla, más bien se nos dan los valores en una fórmula explícita. Las fórmulas surgen en muchas aplicaciones. Por ejemplo, el área de un círculo de radio\(r\) viene dada por la fórmula\(A(r)=πr^2\). Cuando un objeto es arrojado hacia arriba desde el suelo con una velocidad inicial\(v_{0}\) ft/s, su altura sobre el suelo desde el momento en que es lanzado hasta que golpea el suelo viene dada por la fórmula\(s(t)=−16t^2+v_{0}t\). Cuando los\(P\) dólares se invierten en una cuenta a una tasa de interés anual\(r\) compuesta continuamente, la cantidad de dinero después de\(t\) años viene dada por la fórmula\(A(t)=Pe^{rt}\). Las fórmulas algebraicas son herramientas importantes para calcular los valores de las funciones. A menudo también representamos estas funciones visualmente en forma de gráfico.
Dada una fórmula algebraica para una función\(f\), la gráfica de\(f\) es el conjunto de puntos\((x,f(x))\), donde\(x\) está en el dominio de\(f\) y\(f(x)\) está en el rango. Para graficar una función dada por una fórmula, es útil comenzar usando la fórmula para crear una tabla de entradas y salidas. Si el dominio de\(f\) consiste en un número infinito de valores, no podemos enumerarlos todos, pero debido a que enumerar algunas de las entradas y salidas puede ser muy útil, a menudo es una buena manera de comenzar.
Al crear una tabla de entradas y salidas, normalmente verificamos para determinar si cero es una salida. Esos valores de\(x\) donde\(f(x)=0\) se llaman los ceros de una función. Por ejemplo, los ceros de\(f(x)=x^2−4\) son\(x=±2\). Los ceros determinan donde la gráfica de\(f\) cruza el\(x\) eje -eje, lo que nos da más información sobre la forma de la gráfica de la función. La gráfica de una función nunca puede intersectar el\(x\) eje -eje, o puede cruzarse múltiples (o incluso infinitamente muchas) veces.
Otro punto de interés es la\(y\) -intercepción, si existe. La\(y\) -intercepción viene dada por\((0,f(0))\).
Dado que una función tiene exactamente una salida por cada entrada, el gráfico de una función puede tener, como máximo, una\(y\) intersección. Si\(x=0\) está en el dominio de una función\(f,\) entonces\(f\) tiene exactamente una\(y\) -intercepción. Si no\(x=0\) está en el dominio de\(f,\) entonces no\(f\) tiene\(y\) -intercepción. Del mismo modo, para cualquier número real\(c,\) si\(c\) está en el dominio de\(f\), hay exactamente una salida\(f(c),\) y la línea\(x=c\) cruza la gráfica de\(f\) exactamente una vez. Por otro lado, si no\(c\) está en el dominio de no\(f,\)\(f(c)\) está definido y la línea\(x=c\) no se cruza con la gráfica de\(f\). Esta propiedad se resume en la prueba de línea vertical.
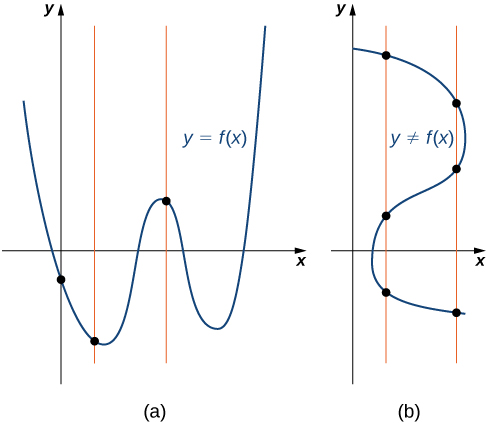
Dada una función\(f\), cada línea vertical que se pueda dibujar cruza la gráfica de\(f\) no más de una vez. Si alguna línea vertical cruza un conjunto de puntos más de una vez, el conjunto de puntos no representa una función.
Podemos utilizar esta prueba para determinar si un conjunto de puntos trazados representa la gráfica de una función (Figura\(\PageIndex{7}\)).
Considera la función\(f(x)=−4x+2.\)
- Encuentra todos los ceros de\(f\).
- Encuentra la\(y\) -intercepción (si la hay).
- Esbozar una gráfica de\(f\).
Solución
1.Para encontrar los ceros, resolver\(f(x)=−4x+2=0\). Descubrimos que\(f\) tiene uno cero en\(x=1/2\).
2. La\(y\) -intercepción viene dada por\((0,f(0))=(0,2).\)
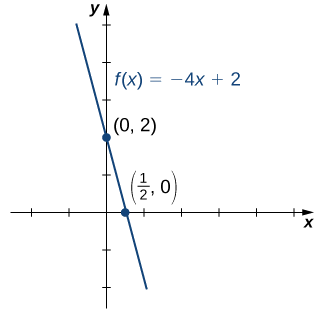
3. Dado que\(f\) es una función lineal de la forma\(f(x)=mx+b\) que pasa por los puntos\((1/2,0)\) y\((0,2)\), podemos bosquejar la gráfica de\(f\) (Figura\(\PageIndex{8}\)).
Considera la función\(f(x)=\sqrt{x+3}+1\).
- Encuentra todos los ceros de\(f\).
- Encuentra la\(y\) -intercepción (si la hay).
- Esbozar una gráfica de\(f\).
Solución
1.Para encontrar los ceros, resolver\(\sqrt{x+3}+1=0\). Esta ecuación implica\(\sqrt{x+3}=−1\). Ya que\(\sqrt{x+3}≥0\) para todos\(x\), esta ecuación no tiene soluciones, y por lo tanto no\(f\) tiene ceros.
2.La\(y\) -intercepción viene dada por\((0,f(0))=(0,\sqrt{3}+1)\).
3.Para graficar esta función, hacemos una tabla de valores. Ya que necesitamos\(x+3≥0\), tenemos que elegir valores de\(x≥−3\). Elegimos valores que facilitan la evaluación de la función de raíz cuadrada.
| \(x\) | -3 | -2 | 1 |
|---|---|---|---|
| \(f(x)\) | 1 | 2 | 3 |
Haciendo uso de la tabla y sabiendo que, dado que la función es una raíz cuadrada, la gráfica de\(f\) debe ser similar a la gráfica de\(y=\sqrt{x}\), esbozamos la gráfica (Figura\(\PageIndex{9}\)).
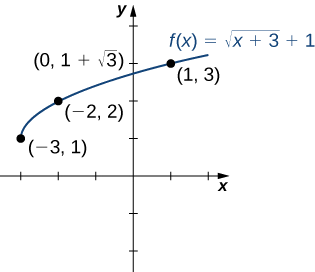
Encuentra los ceros de\(f(x)=x^3−5x^2+6x.\)
- Pista
-
Facturar el polinomio.
- Responder
-
\(x=0,2,3\)
Si se cae una pelota desde una altura de 100 pies, su altura s en el momento\(t\) viene dada por la función\(s(t)=−16t^2+100\), donde s se mide en pies y\(t\) se mide en segundos. El dominio está restringido al intervalo\([0,c],\) donde\(t=0\) es el momento en que se cae la pelota y\(t=c\) es el momento en que la pelota golpea el suelo.
- Crear una tabla que muestre la altura s (t) cuando\(t=0,\, 0.5,\, 1,\, 1.5,\, 2,\) y\(2.5\). Usando los datos de la tabla, determine el dominio para esta función. Es decir, encuentra el\(c\) momento en que la pelota golpea el suelo.
- Esbozar una gráfica de\(s\).
Solución
| \(t\) | 0 | 0.5 | 1 | 1.5 | 2 | 2.5 |
| \(s(t)\) | 100 | 96 | 84 | 64 | 36 | 0 |
Ya que la pelota golpea el suelo cuando\(t=2.5\), el dominio de esta función es el intervalo\([0,2.5]\).
2.
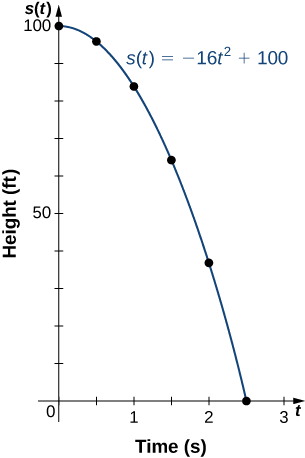
Decimos que una función\(f\) está aumentando en el intervalo\(I\) si para todos\(x_{1},\, x_{2}∈I,\)
\(f(x_{1})≤f(x_{2})\)cuando\(x_{1}<x_{2}.\)
Decimos que\(f\) está aumentando estrictamente en el intervalo\(I\) si para todos\(x_{1},x_{2}∈I,\)
\(f(x_{1})<f(x_{2})\)cuando\(x_{1}<x_{2}.\)
Decimos que una función\(f\) está disminuyendo en el intervalo\(I\) si para todos\(x_{1},x_{2}∈I,\)
\(f(x_{1})≥f(x_{2})\)si\(x_{1}<x_{2}.\)
Decimos que una función\(f\) es estrictamente decreciente en el intervalo\(I\) si para todos\(x_{1},x_{2}∈I\),
\(f(x_{1})>f(x_{2})\)si\(x_{1}<x_{2}.\)
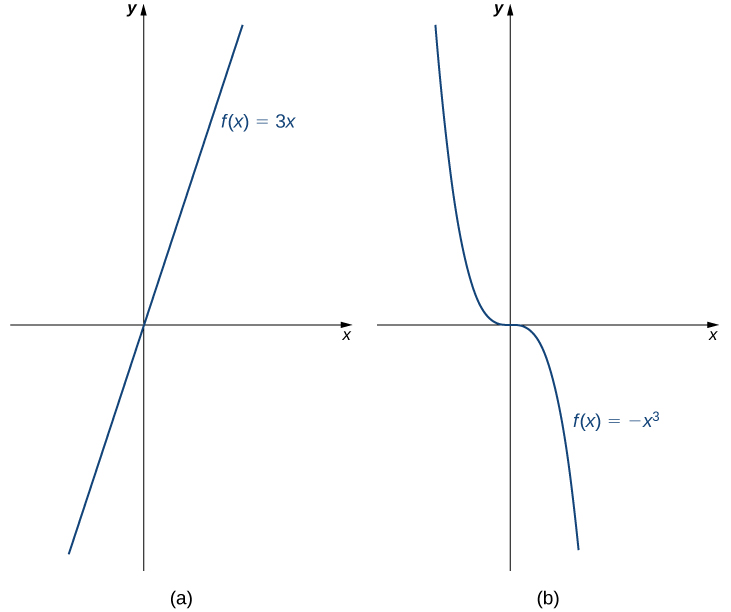
Por ejemplo, la función\(f(x)=3x\) está aumentando en el intervalo\((−∞,∞)\) porque\(3x_{1}<3x_{2}\) siempre que sea\(x_{1}<x_{2}\). Por otro lado, la función\(f(x)=−x^3\) está disminuyendo en el intervalo\((−∞,∞)\) porque\(−x^3_{1}>−x^3_{2}\) siempre que sea\(x_{1}<x_{2}\) (Figura\(\PageIndex{10}\)).
Combinar funciones
Ahora que hemos revisado las características básicas de las funciones, podemos ver qué sucede con estas propiedades cuando combinamos funciones de diferentes maneras, utilizando operaciones matemáticas básicas para crear nuevas funciones. Por ejemplo, si el costo para que una empresa fabrique\(x\) artículos es descrito por la función\(C(x)\) y el ingreso creado por la venta de\(x\) artículos es descrito por la función\(R(x)\), entonces el beneficio en la fabricación y venta de\(x\) artículos se define como\(P(x)=R(x)−C(x)\). Usando la diferencia entre dos funciones, creamos una nueva función.
Alternativamente, podemos crear una nueva función componiendo dos funciones. Por ejemplo, dadas las funciones\(f(x)=x^2\) y\(g(x)=3x+1\), la función compuesta\(f∘g\) se define de tal manera que
\[(f∘g)(x)=f(g(x))=(g(x))^2=(3x+1)^2. \nonumber \]
La función compuesta\(g∘f\) se define de tal manera que
\[(g∘f)(x)=g(f(x))=3f(x)+1=3x^2+1. \nonumber \]
Tenga en cuenta que estas dos nuevas funciones son diferentes entre sí.
Combinar funciones con operadores matemáticos
Para combinar funciones usando operadores matemáticos, simplemente escribimos las funciones con el operador y simplificamos. Dadas dos funciones\(f\) y\(g\), podemos definir cuatro nuevas funciones:
| \((f+g)(x)=f(x)+g(x)\) | Suma |
| \((f−g)(x)=f(x)−g(x)\) | Diferencia |
| \((f·g)(x)=f(x)g(x)\) | Producto |
| \((\frac{f}{g})(x)=\frac{f(x)}{g(x)}\)para\(g(x)≠0\) | Cociente |
Dadas las funciones\(f(x)=2x−3\) y\(g(x)=x^2−1\), encontrar cada una de las siguientes funciones y exponer su dominio.
- \((f+g)(x)\)
- \((f−g)(x)\)
- \((f·g)(x)\)
- \(\left(\dfrac{f}{g}\right)(x)\)
Solución
1. \((f+g)(x)=(2x−3)+(x^2−1)=x^2+2x−4.\)
El dominio de esta función es el intervalo\((−∞,∞)\).
2. \((f−g)(x)=(2x−3)−(x^2−1)=−x^2+2x−2.\)
El dominio de esta función es el intervalo\((−∞,∞)\).
3. \((f·g)(x)=(2x−3)(x^2−1)=2x^3−3x^2−2x+3.\)
El dominio de esta función es el intervalo\((−∞,∞)\).
4. \(\left(\dfrac{f}{g}\right)(x)=\dfrac{2x−3}{x^2−1}\).
El dominio de esta función es\(\{x\,|\,x≠±1\}.\)
Para\(f(x)=x^2+3\) y\(g(x)=2x−5\), encontrar\((f/g)(x)\) y exponer su dominio.
- Pista
-
La nueva función\((f/g)(x)\) es un cociente de dos funciones. ¿Para qué valores de\(x\) es el denominador cero?
- Responder
-
\(\left(\dfrac{f}{g}\right)(x)=\frac{x^2+3}{2x−5}.\)El dominio es\(\{x\,|\,x≠\frac{5}{2}\}.\)
Composición de la función
Cuando componemos funciones, tomamos una función de una función. Por ejemplo, supongamos que la temperatura\(T\) en un día dado se describe como una función del tiempo\(t\) (medido en horas después de la medianoche) como en la Tabla\(\PageIndex{1}\). Supongamos que el costo\(C\), calentar o enfriar un edificio durante 1 hora, puede describirse como una función de la temperatura\(T\). Combinando estas dos funciones, podemos describir el costo de calentar o enfriar un edificio en función del tiempo evaluando\(C(T(t))\). Hemos definido una nueva función, denotada\(C∘T\), que se define de tal manera que\((C∘T)(t)=C(T(t))\) para todos\(t\) en el dominio de\(T\). Esta nueva función se llama función compuesta. Observamos que dado que el costo es una función de la temperatura y la temperatura es una función del tiempo, tiene sentido definir esta nueva función\((C∘T)(t)\). No tiene sentido considerar\((T∘C)(t)\), porque la temperatura no es una función del costo.
Considere la función\(f\) con dominio\(A\) y rango\(B\), y la función\(g\) con dominio\(D\) y rango\(E\). Si\(B\) es un subconjunto de\(D\), entonces la función compuesta\((g∘f)(x)\) es la función con dominio\(A\) tal que
\[(g∘f)(x)=g(f(x)) \nonumber \]
Una función compuesta se\(g∘f\) puede ver en dos pasos. Primero, la función\(f\) mapea cada entrada\(x\) en el dominio de\(f\) a su salida\(f(x)\) en el rango de\(f\). En segundo lugar, dado que el rango de\(f\) es un subconjunto del dominio de\(g\), la salida\(f(x)\) es un elemento en el dominio de\(g\), y por lo tanto se mapea a una salida\(g(f(x))\) en el rango de\(g\). En la Figura\(\PageIndex{11}\), vemos una imagen visual de una función compuesta.
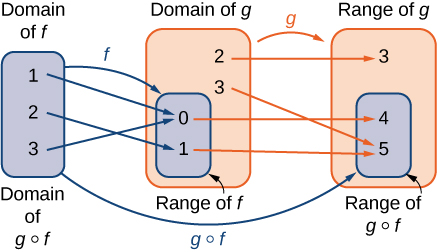
Considerar las funciones\(f(x)=x^2+1\) y\(g(x)=1/x\).
- Encontrar\((g∘f)(x)\) y exponer su dominio y alcance.
- Evaluar\((g∘f)(4),\)\((g∘f)(−1/2)\).
- Encontrar\((f∘g)(x)\) y exponer su dominio y alcance.
- Evaluar\((f∘g)(4),\)\((f∘g)(−1/2)\).
Solución
1. Podemos encontrar la fórmula para\((g∘f)(x)\) de dos maneras diferentes. Podríamos escribir
\((g∘f)(x)=g(f(x))=g(x^2+1)=\dfrac{1}{x^2+1}\).
Alternativamente, podríamos escribir
\((g∘f)(x)=g(f(x))=\dfrac{1}{f(x)}=\dfrac{1}{x^2+1}.\)
Ya que\(x^2+1≠0\) para todos los números reales\(x,\) el dominio de\((g∘f)(x)\) es el conjunto de todos los números reales. Ya que\(0<1/(x^2+1)≤1\), el rango es, a lo sumo, el intervalo\((0,1]\). Para demostrar que el rango es todo este intervalo, dejamos\(y=1/(x^2+1)\) y resolvemos esta ecuación\(x\) para mostrar que para todos\(y\) en el intervalo\((0,1]\), existe un número real\(x\) tal que\(y=1/(x^2+1)\). Resolviendo esta ecuación para que\(x,\) veamos eso\(x^2+1=1/y\), lo que implica que
\(x=±\sqrt{\frac{1}{y}−1}\)
Si\(y\) está en el intervalo\((0,1]\), la expresión bajo el radical no es negativa, y por lo tanto existe un número real\(x\) tal que\(1/(x^2+1)=y\). Concluimos que el rango de\(g∘f\) es el intervalo\((0,1].\)
2. \((g∘f)(4)=g(f(4))=g(4^2+1)=g(17)=\frac{1}{17}\)
\((g∘f)(−\frac{1}{2})=g(f(−\frac{1}{2}))=g((−\frac{1}{2})^2+1)=g(\frac{5}{4})=\frac{4}{5}\)
3. Podemos encontrar una fórmula para\((f∘g)(x)\) de dos maneras. Primero, podríamos escribir
\((f∘g)(x)=f(g(x))=f(\frac{1}{x})=(\frac{1}{x})^2+1.\)
Alternativamente, podríamos escribir
\((f∘g)(x)=f(g(x))=(g(x))^2+1=(\frac{1}{x})^2+1.\)
El dominio de\(f∘g\) es el conjunto de todos los números reales\(x\) tales que\(x≠0\). Para encontrar el rango de\(f,\) necesitamos encontrar todos los valores\(y\) para los que existe un número real\(x≠0\) tal que
\(\left(\dfrac{1}{x}\right)^2+1=y.\)
Resolviendo esta ecuación para\(x,\) vemos que necesitamos\(x\) satisfacer
\(\left(\dfrac{1}{x}\right)^2=y−1,\)
lo que simplifica a
\(\dfrac{1}{x}=±\sqrt{y−1}\)
Finalmente, obtenemos
\(x=±\dfrac{1}{\sqrt{y−1}}.\)
Dado que\(1/\sqrt{y−1}\) es un número real si y sólo si\(y>1,\) el rango de\(f\) es el conjunto\(\{y\,|\,y≥1\}.\)
4. \((f∘g)(4)=f(g(4))=f(\frac{1}{4})=(\frac{1}{4})^2+1=\frac{17}{16}\)
\((f∘g)(−\frac{1}{2})=f(g(−\frac{1}{2}))=f(−2)=(−2)^2+1=5\)
En Ejemplo\(\PageIndex{7}\), podemos ver eso\((f∘g)(x)≠(g∘f)(x)\). Esto nos dice, en términos generales, que importa el orden en que componemos las funciones.
Vamos\(f(x)=2−5x\). Vamos a\(g(x)=\sqrt{x}.\) encontrar\((f∘g)(x)\).
Solución
\((f∘g)(x)=2−5\sqrt{x}.\)
Considere las funciones\(f\) y\(g\) descritas por
| \(x\) | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|---|---|---|
| \(f(x)\) | 0 | 4 | 2 | 4 | -2 | 0 | -2 | 4 |
| \(x\) | -4 | -2 | 0 | 2 | 4 |
|---|---|---|---|---|---|
| \(g(x)\) | 1 | 0 | 3 | 0 | 5 |
- Evaluar\((g∘f)(3)\),\((g∘f)(0)\).
- Indicar el dominio y el rango de\((g∘f)(x)\).
- Evaluar\((f∘f)(3)\),\((f∘f)(1)\).
- Indicar el dominio y el rango de\((f∘f)(x)\).
Solución:
1. \((g∘f)(3)=g(f(3))=g(−2)=0\)
\((g∘f)(0)=g(4)=5\)
2.El dominio de\(g∘f\) es el conjunto\(\{−3,−2,−1,0,1,2,3,4\}.\) Dado que el rango de\(f\) es el conjunto,\(\{−2,0,2,4\},\) el rango de\(g∘f\) es el conjunto\(\{0,3,5\}.\)
3. \((f∘f)(3)=f(f(3))=f(−2)=4\)
\((f∘f)(1)=f(f(1))=f(−2)=4\)
4.El dominio de\(f∘f\) es el conjunto\(\{−3,−2,−1,0,1,2,3,4\}.\) Dado que el rango de\(f\) es el conjunto,\(\{−2,0,2,4\},\) el rango de\(f∘f\) es el conjunto\(\{0,4\}.\)
Una tienda está anunciando una venta de 20% de descuento en toda la mercancía. Caroline tiene un cupón que le da derecho a un 15% de descuento adicional en cualquier artículo, incluida la mercancía de venta. Si Caroline decide comprar un artículo con un precio original de\(x\) dólares, ¿cuánto terminará pagando si aplica su cupón al precio de venta? Resolver este problema usando una función compuesta.
Solución
Ya que el precio de venta es 20% de descuento sobre el precio original, si un artículo es\(x\) dólares, su precio de venta es dado por\(f(x)=0.80x\). Dado que el cupón da derecho a un individuo a 15% de descuento en el precio de cualquier artículo, si un artículo es\(y\) dólares, el precio, después de aplicar el cupón, viene dado por g (y) =0.85y. Por lo tanto, si el precio es originalmente\(x\) dólares, su precio de venta será\(f(x)=0.80x\) y luego su precio final después del cupón será\(g(f(x))=0.85(0.80x)=0.68x\).
Si los artículos están a la venta por un 10% de descuento en su precio original, y un cliente tiene un cupón por un 30% de descuento adicional, ¿cuál será el precio final de un artículo que originalmente es\(x\) dólares, después de aplicar el cupón al precio de venta?
Pista
El precio de venta de un artículo con un precio original de\(x\) dólares es\(f(x)=0.90x\). El precio del cupón para un artículo que es\(y\) dólares es\(g(y)=0.70y\).
Solución
\((g∘f)(x)=0.63x\)
Simetría de funciones
Las gráficas de ciertas funciones tienen propiedades de simetría que nos ayudan a entender la función y la forma de su gráfica. Por ejemplo, considere la función que\(f(x)=x^4−2x^2−3\) se muestra en la Figura\(\PageIndex{12a}\). Si tomamos la parte de la curva que se encuentra a la derecha del\(y\) eje -y la volteamos sobre el\(y\) eje -eje, se coloca exactamente en la parte superior de la curva a la izquierda del\(y\) eje -axis. En este caso, decimos que la función tiene simetría alrededor del\(y\) eje -eje. Por otro lado, considere la función que\(f(x)=x^3−4x\) se muestra en la Figura\(\PageIndex{12b}\). Si tomamos la gráfica y la giramos\(180°\) sobre el origen, la nueva gráfica se verá exactamente igual. En este caso, decimos que la función tiene simetría sobre el origen.
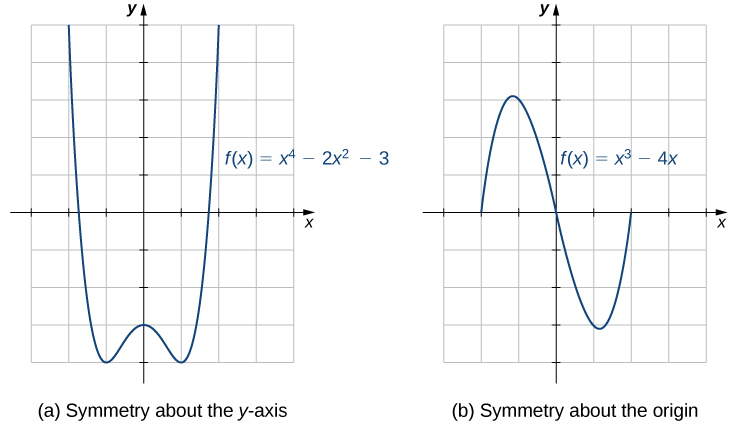
Si se nos da la gráfica de una función, es fácil ver si la gráfica tiene una de estas propiedades de simetría. Pero sin una gráfica, ¿cómo podemos determinar algebraicamente si una función\(f\) tiene simetría? Al mirar Figura\(\PageIndex{12a}\) nuevamente, vemos que ya que\(f\) es simétrico alrededor del\(y\) eje -eje, si el punto\((x,y)\) está en la gráfica, el punto\((−x,y)\) está en la gráfica. En otras palabras,\(f(−x)=f(x)\). Si una función\(f\) tiene esta propiedad, decimos que\(f\) es una función par, que tiene simetría alrededor del\(y\) eje -eje. Por ejemplo,\(f(x)=x^2\) es incluso porque
\(f(−x)=(−x)^2=x^2=f(x).\)
En contraste, mirando\(\PageIndex{12b}\) nuevamente a Figura, si una función\(f\) es simétrica sobre el origen, entonces siempre que el punto\((x,y)\) esté en la gráfica, el punto también\((−x,−y)\) está en la gráfica. En otras palabras,\(f(−x)=−f(x)\). Si\(f\) tiene esta propiedad, decimos que\(f\) es una función impar, que tiene simetría sobre el origen. Por ejemplo,\(f(x)=x^3\) es impar porque
\(f(−x)=(−x)^3=−x^3=−f(x).\)
- Si\(f(x)=f(−x)\) para todos\(x\) en el dominio de\(f\), entonces\(f\) es una función par. Una función par es simétrica alrededor del\(y\) eje.
- Si\(f(−x)=−f(x)\) para todos\(x\) en el dominio de\(f\), entonces\(f\) es una función impar. Una función impar es simétrica sobre el origen.
Determina si cada una de las siguientes funciones es par, impar o ninguna.
- \(f(x)=−5x^4+7x^2−2\)
- \(f(x)=2x^5−4x+5\)
- \(f(x)=\frac{3x}{x^2+1}\)
Solución
Para determinar si una función es par o impar, la evaluamos\(f(−x)\) y comparamos con\(f(x)\) y\(−f(x)\).
1. \(f(−x)=−5(−x)^4+7(−x)^2−2=−5x^4+7x^2−2=f(x).\)Por lo tanto,\(f\) es parejo.
2. \(f(−x)=2(−x)^5−4(−x)+5=−2x^5+4x+5.\)Ahora,\(f(−x)≠f(x).\) además, al señalar que\(−f(x)=−2x^5+4x−5\), vemos eso\(f(−x)≠−f(x)\). Por lo tanto, no\(f\) es ni par ni impar.
3. \(f(−x)=3(−x)/((−x)2+1)\)\(=−3x/(x^2+1)=\)\(−[3x/(x^2+1)]=−f(x).\)Por lo tanto,\(f\) es extraño.
Determinar si\(f(x)=4x^3−5x\) es par, impar o ninguno.
- Pista
-
Comparar\(f(−x)\) con\(f(x)\) y\(−f(x)\).
- Responder
-
\(f(x)\)es impar.
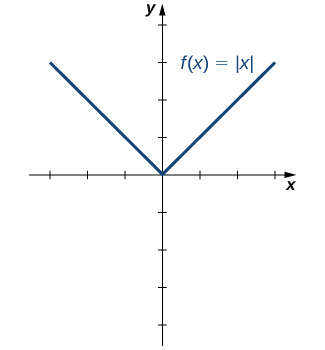
Una función simétrica que surge frecuentemente es la función de valor absoluto, escrita como\(|x|\). La función de valor absoluto se define como
\[f(x)=\begin{cases} -x, & \text{if }x<0 \\ x, & \text{if } x≥0 \end{cases} \nonumber \]
Algunos alumnos describen esta función afirmando que “hace que todo sea positivo”. Por la definición de la función de valor absoluto, vemos que si\(x<0\), entonces\(|x|=−x>0,\) y si\(x>0\), entonces\(|x|=x>0.\) Sin embargo, para\(x=0,\)\(|x|=0.\) Por lo tanto, es más preciso decir que para todas las entradas distintas de cero, la salida es positiva, pero si\(x=0\), la salida\(|x|=0\). Concluimos que el rango de la función de valor absoluto es\(\{y\,|\,y≥0\}.\) En Figura\(\PageIndex{13}\), vemos que la función de valor absoluto es simétrica alrededor del\(y\) eje -y por lo tanto es una función par.
Encuentra el dominio y el rango de la función\(f(x)=2|x−3|+4\).
Solución
Dado que la función de valor absoluto está definida para todos los números reales, el dominio de esta función es\((−∞,∞)\). Ya que\(|x−3|≥0\) para todos\(x\), la función\(f(x)=2|x−3|+4≥4\). Por lo tanto, el rango es,\(\{y\,|\,y≥4\}.\) a lo sumo, el conjunto Para ver que el rango es, de hecho, todo este conjunto, necesitamos demostrar que para\(y≥4\) existe un número real\(x\) tal que
\(2|x−3|+4=y\)
Un número real\(x\) satisface esta ecuación siempre que
\(|x−3|=\frac{1}{2}(y−4)\)
Ya que\(y≥4\), sabemos\(y−4≥0\), y así el lado derecho de la ecuación no es negativo, por lo que es posible que haya una solución. Además,
\(|x−3|=\begin{cases} −(x−3), & \text{if } x<3\\x−3, & \text{if } x≥3\end{cases}\)
Por lo tanto, vemos que hay dos soluciones:
\(x=±\frac{1}{2}(y−4)+3\).
El rango de esta función es\(\{y\,|\,y≥4\}.\)
Para la función\(f(x)=|x+2|−4\), encuentra el dominio y el rango.
- Pista
-
\(|x+2|≥0\)para todos los números reales\(x\).
- Responder
-
Dominio =\((−∞,∞)\), rango =\(\{y\,|\,y≥−4\}.\)
Conceptos clave
- Una función es un mapeo de un conjunto de entradas a un conjunto de salidas con exactamente una salida para cada entrada.
- Si no se establece ningún dominio para una función, se considera que\(y=f(x),\) el dominio es el conjunto de todos los números reales\(x\) para los que se define la función.
- Al esbozar la gráfica de una función,\(f,\) cada línea vertical puede intersectar la gráfica, como máximo, una vez.
- Una función puede tener cualquier número de ceros, pero tiene, como mucho, una\(y\) intercepción.
- Para definir la composición\(g∘f\), el rango de\(f\) debe estar contenido en el dominio de\(g\).
- Las funciones pares son simétricas alrededor del\(y\) eje, mientras que las funciones impares son simétricas sobre el origen.
Ecuaciones Clave
- Composición de dos funciones
\((g∘f)(x)=g\big(f(x)\big)\)
- Función de valor absoluto
\(f(x)=\begin{cases}−x, & \text{if } x<0\\x, & \text{if } x≥0\end{cases}\)
Glosario
- función de valor absoluto
- \(f(x)=\begin{cases}−x, & \text{if } x<0\\x, & \text{if } x≥0\end{cases}\)
- función compuesta
- dadas dos funciones\(f\) y\(g\), una nueva función, denotada\(g∘f\), tal que\((g∘f)(x)=g(f(x))\)
- decreciente en el intervalo\(I\)
- una función decreciente en el intervalo\(I\) si, para todos\(x_1,\,x_2∈I,\;f(x_1)≥f(x_2)\) si\(x_1<x_2\)
- variable dependiente
- la variable de salida para una función
- dominio
- el conjunto de entradas para una función
- incluso función
- una función es incluso si\(f(−x)=f(x)\) para todos\(x\) en el dominio de\(f\)
- función
- un conjunto de entradas, un conjunto de salidas y una regla para mapear cada entrada a exactamente una salida
- gráfico de una función
- el conjunto de puntos\((x,y)\) tal que\(x\) está en el dominio de\(f\) y\(y=f(x)\)
- aumentando en el intervalo\(I\)
- una función que aumenta en el intervalo\(I\) si para todos\(x_1,\,x_2∈I,\;f(x_1)≤f(x_2)\) si\(x_1<x_2\)
- variable independiente
- la variable de entrada para una función
- función impar
- una función es impar si\(f(−x)=−f(x)\) para todos\(x\) en el dominio de\(f\)
- gama
- el conjunto de salidas para una función
- simetría sobre el origen
- la gráfica de una función\(f\) es simétrica sobre el origen si\((−x,−y)\) está en la gráfica de\(f\) siempre que\((x,y)\) esté en la gráfica
- simetría sobre el\(y\) eje
- la gráfica de una función\(f\) es simétrica sobre el\(y\) eje -si\((−x,y)\) está en la gráfica de\(f\) siempre que\((x,y)\) esté en la gráfica
- tabla de valores
- una tabla que contiene una lista de entradas y sus correspondientes salidas
- prueba de línea vertical
- dada la gráfica de una función, cada línea vertical se cruza con la gráfica, a lo sumo, una vez
- ceros de una función
- cuando un número real\(x\) es un cero de una función\(f,\;f(x)=0\)


