3.5: Ceros reales de polinomios

Última actualización
Guardar como PDF

Page ID: 116520

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

En la última sección, vimos cómo determinar si un número real era un cero de un polinomio. En esta sección, aprenderemos a encontrar buenos candidatos para probar usando división sintética. En los días previos a que la tecnología gráfica fuera algo común, los matemáticos descubrieron muchos trucos inteligentes para determinar las ubicaciones probables de los ceros. La tecnología ha proporcionado un enfoque mucho más simple para acotar a los candidatos potenciales, pero no siempre es suficiente por sí misma. Por ejemplo, la función que se muestra a la derecha no tiene ninguna intercepción clara.

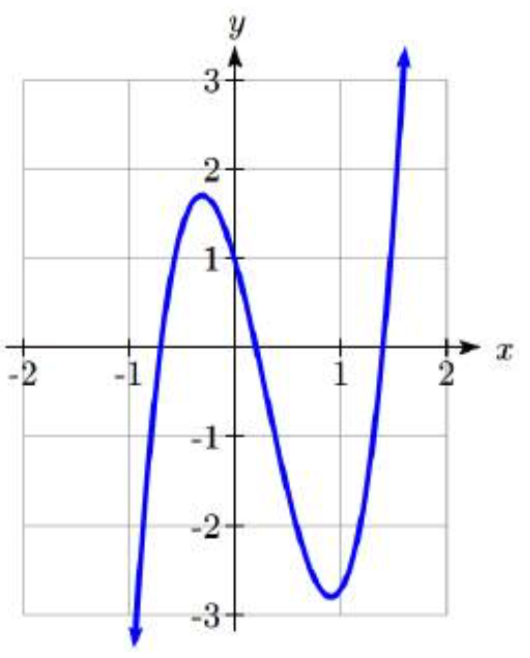
$Un gráfico cúbico que cruza el eje x en tres ubicaciones no enteras poco claras.$

Hay dos resultados que pueden ayudarnos a identificar dónde están los ceros de un polinomio. El primero nos da un intervalo en el que se pueden encontrar todos los ceros reales de un polinomio.

Definición: Cauchy's Bound

Dado un polinomio

\[(f(x)=a_{n} x^{n} +a_{n-1} x^{n-1} +\cdots +a_{1} x+a_{0},\]

dejar$M$ ser el mayor de los coeficientes en valor absoluto. Entonces todos los ceros reales de$f(x)$ mentira en el intervalo

\[\left[-\dfrac{M}{\left|a_{n} \right|} -1,\quad \dfrac{M}{\left|a_{n} \right|} +1\right] \label{Cauchy}\]

Ejemplo 1

Vamos$f(x)=2x^{4} +4x^{3} -x^{2} -6x-3$. Determinar un intervalo que contenga todos los ceros reales de f.

Solución

Para encontrar el$M$ de Cauchy's Bound, tomamos el valor absoluto de los coeficientes y escogemos el más grande, en este caso$\left|-6\right|=6$. Divide esto por el valor absoluto del coeficiente principal, 2, para obtener 3. Todos los ceros reales de f se encuentran en el intervalo

\[\left[-\dfrac{6}{\left|2\right|} -1,\quad \dfrac{6}{\left|2\right|} +1\right]=\left[-3-1,\quad 3+1\right]=[-4,\; 4]. \nonumber\]

Conocer este límite puede ser muy útil a la hora de usar una calculadora gráfica, ya que podemos usarla para establecer los límites de visualización. Esto ayuda a evitar perder un cero porque está graficado fuera de la ventana de visualización.

Ejercicio$\PageIndex{1}$

Determinar un intervalo que contiene todos los ceros reales de$f(x)=3x^{3} -12x^{2} +6x-8$.

Contestar

El coeficiente máximo en valor absoluto es 12. Cauchy's Bound para todos los ceros reales es

\[\left[-\dfrac{12}{\left|3\right|} -1,\quad \dfrac{12}{\left|3\right|} +1\right]=[-5,5]\nonumber \]

Ahora que sabemos dónde podemos encontrar los ceros reales, todavía necesitamos una lista de posibles ceros reales. El teorema de las raíces racionales nos proporciona una lista de enteros potenciales y ceros racionales.

teorema de raíces racionales

Dado un polinomio

\[f(x)=a_{n} x^{n} +a_{n-1} x^{n-1} +\cdots +a_{1} x+a_{0}\]

con coeficientes enteros, si$r$ es un cero racional de$f$, entonces$r$ es de la forma$r=\pm \dfrac{p}{q}$, donde$p$ es un factor del término constante$a_{0}$, y$q$ es un factor del coeficiente principal,$a_{n}$.

Esto nos da una lista de números para probar en nuestra división sintética, que es un mejor lugar para comenzar que simplemente adivinar. Si ninguno de los números de la lista son ceros, entonces o el polinomio no tiene ceros reales en absoluto, o todos los ceros reales son números irracionales.

Ejemplo$\PageIndex{2}$

Vamos$f(x)=2x^{4} +4x^{3} -x^{2} -6x-3$. Utilice el Teorema de Raíces Racionales para enumerar todos los ceros racionales posibles de$f(x)$.

Solución

Para generar una lista completa de ceros racionales, necesitamos tomar cada uno de los factores de la

término constante,$a_{0} =-3$, y dividirlos por cada uno de los factores del coeficiente principal$a_{4} =2$. Los factores de -3 son$\pm 1$ y$\pm 3$. Dado que el Teorema de Raíces Racionales tachuelas en una de$\pm$ todas formas, por el momento, consideramos solo los factores positivos 1 y 3. Los factores de 2 son 1 y 2, por lo que el Teorema de Raíces Racionales da la lista

\[\left\{\pm \dfrac{1}{1} ,\pm \dfrac{1}{2} ,\pm \dfrac{3}{1} ,\pm \dfrac{3}{2} \right\}\text{ ,or }\left\{\pm 1,\pm \dfrac{1}{2} ,\pm 3,\pm \dfrac{3}{2} \right\}\nonumber \]

Ahora podemos usar división sintética para probar estos posibles ceros. Para estrechar la lista primero, podríamos usar tecnología gráfica para ayudarnos a identificar algunas buenas posibilidades.

Ejemplo$\PageIndex{3}$

Encuentra las intercepciones horizontales de$f(x)=2x^{4} +4x^{3} -x^{2} -6x-3$.

Solución

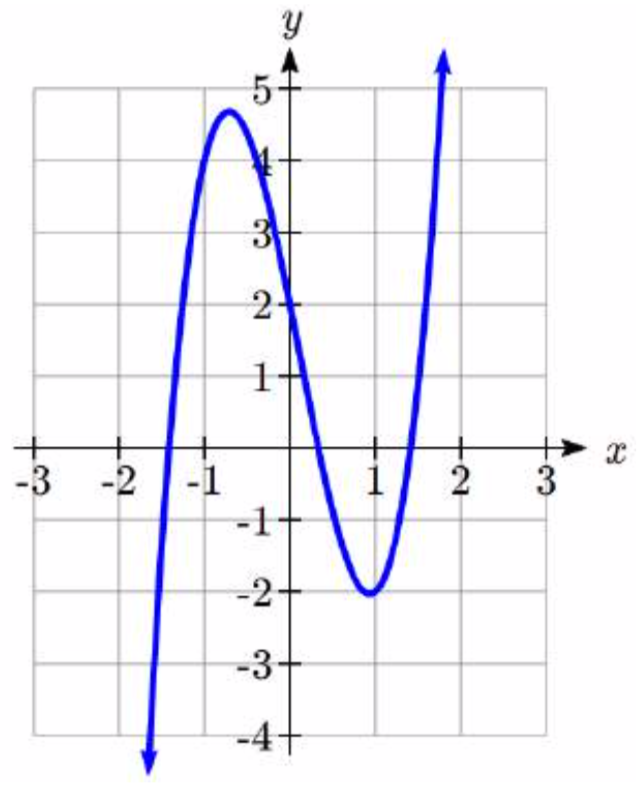
Del Ejemplo 1, sabemos que los ceros reales se encuentran en el intervalo [-4, 4]. Usando una calculadora gráfica, podríamos establecer la ventana en consecuencia y obtener el gráfico a continuación.

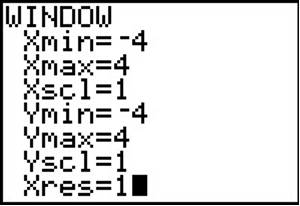
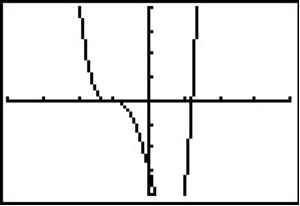
$Una imagen de una página de ventana de calculadora gráfica, que muestra xmin es igual a -4, xmax es igual a 4, xscl es igual a 1, ymin es igual a -4, ymax es igual a 4, yscl es igual a 1, xres es igual a 1.$ $Una imagen de una gráfica de 2 x a la cuarta más 4 x cubos menos x al cuadrado menos 6 x menos 3 en una calculadora gráfica. La gráfica tiene intercepciones x en negativo 1 y otro valor alrededor de 1.2.$

En el Ejemplo 2, aprendimos que cualquier cero racional debe estar en la lista$\left\{\pm 1,\pm \dfrac{1}{2} ,\pm 3,\pm \dfrac{3}{2} \right\}$. De la gráfica, parece que -1 es una buena posibilidad, así que lo intentamos usando división sintética.

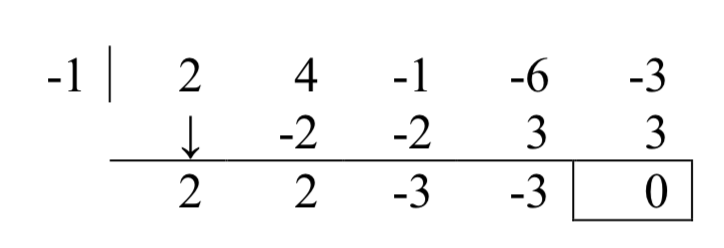
$2019-06-23 7.53.30.png$

¡Éxito! Recordando que$f$ era un polinomio de cuarto grado, sabemos que nuestro cociente es un polinomio de tercer grado. Si podemos hacer una división más exitosa, habremos derribado el cociente a una cuadrática, y, si todo lo demás falla, podremos usar la fórmula cuadrática para encontrar los dos últimos ceros. Como parece que no hay otros ceros racionales que probar, seguimos con -1. Además, la forma del cruce en nos$x = -1$ lleva a preguntarnos si el cero$x = -1$ tiene multiplicidad 3.

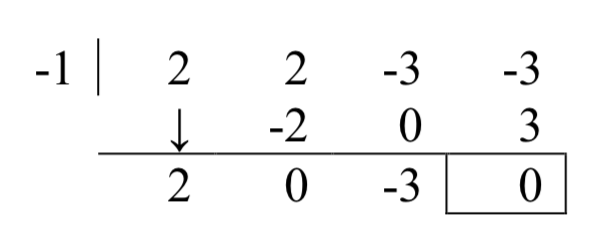
$2019-06-23 7.54.36.png$

¡Éxito otra vez! Nuestro polinomio cociente es ahora$2x^{2} -3$. Poner esto a cero da$2x^{2} -3=0$, dando$x=\pm \sqrt{\dfrac{3}{2} } =\pm \dfrac{\sqrt{6} }{2}$. Dado que un polinomio de cuarto grado puede tener como máximo cuatro ceros, incluyendo multiplicidades, entonces la intercepción x = -1 solo debe tener multiplicidad 2, que habíamos encontrado a través de la división, y no 3 como habíamos adivinado.

Es interesante señalar que podríamos mejorar mucho en la gráfica de$y=f(x)$ en el ejemplo anterior que nos dio la calculadora. Por ejemplo, a partir de nuestra determinación de los ceros de$f$ y sus multiplicidades, sabemos que la gráfica cruza en$x=-\dfrac{\sqrt{6} }{2} \approx -1.22$ luego vuelve hacia arriba para tocar el$x$ eje en$x = -1$. Esto nos dice que, a pesar de lo que la calculadora nos mostró la primera vez, hay un máximo relativo que ocurre en$x = -1$ y no un “cruce aplanado” como originalmente creíamos.

Después de redimensionar la ventana, vemos no solo el máximo relativo sino también un mínimo relativo justo a la izquierda de$x = -1$

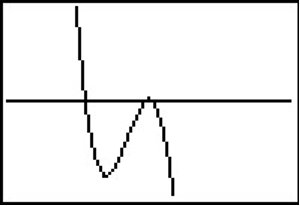
$Una imagen de una página de ventana de calculadora gráfica, que muestra xmin es igual a -1.5, xmax es igual a -0.5, xscl es igual a 1, ymin es igual a -0.01, ymax igual a 0.01, yscl es igual a 1, xres es igual a 1.$ $Un gráfico con zoom que muestra una intercepción x en negativo 1 y otra x intercepción ligeramente a la izquierda de la misma.$

En este caso, las matemáticas ayudaron a revelar algo que estaba oculto en la gráfica inicial.

Ejemplo 4

Encuentra los ceros reales de$f(x)=4x^{3} -10x^{2} -2x+2$.

Solución

$Una gráfica cúbica cruza el eje x en tres puntos poco claros. El primero está entre 1 y 0 negativo, el segundo entre 0 y 1, y el tercero entre 2 y 3.$ Cauchy's Bound nos dice que los ceros reales se encuentran en el intervalo$\left[-\dfrac{10}{\left|4\right|} -1,\quad \dfrac{10}{\left|4\right|} +1\right]=[-3.5,\; 3.5]$.

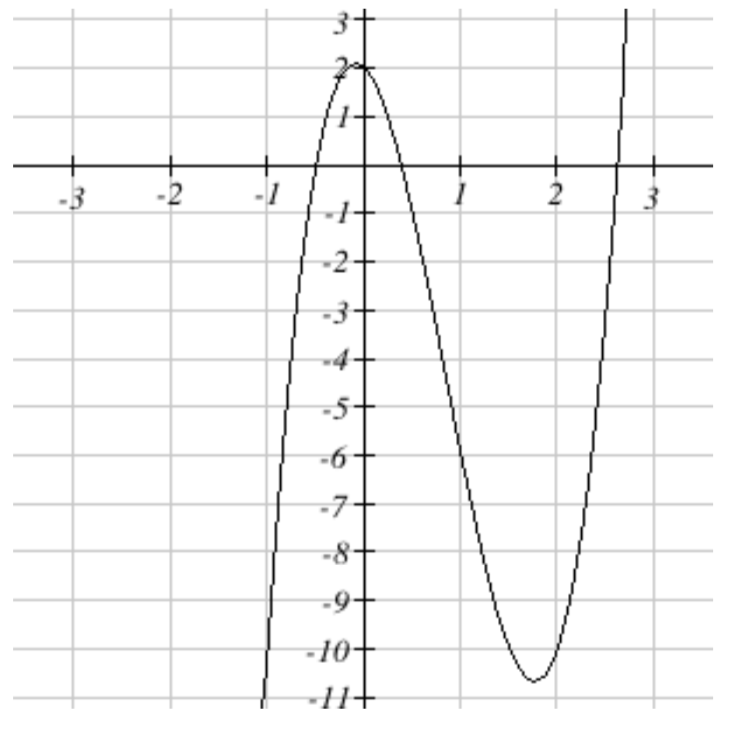
Graficar en este intervalo no revela ceros enteros claros. Volviendo al teorema de raíces racionales, necesitamos tomar cada uno de los factores del término constante,$a_{0} =2$, y dividirlos por cada uno de los factores del coeficiente principal$a_{3} =4$. Los factores de 2 son 1 y 2. Los factores de 4 son 1, 2 y 4, por lo que el Teorema de Raíces Racionales da la lista

\[\left\{\pm \dfrac{1}{1} ,\pm \dfrac{1}{2} ,\pm \dfrac{1}{4} ,\pm \dfrac{2}{1} ,\pm \dfrac{2}{2} ,\pm \dfrac{2}{4} \right\}\text{ ,or }\left\{\pm 1,\pm \dfrac{1}{2} ,\pm \dfrac{1}{4} ,\pm 2\right\}\nonumber \]

Los dos candidatos más probables son$\pm \dfrac{1}{2}$.

Intentando$\dfrac{1}{2}$,

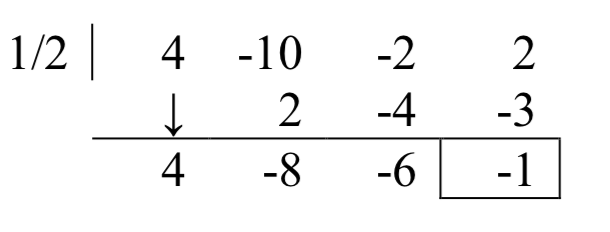
$2019-06-23 7.59.25.png$

El resto no es cero, así que esto no es un cero. Intentando$-\dfrac{1}{2}$,

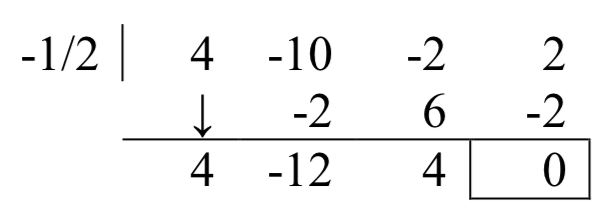
$2019-06-23 7.59.41.png$

¡Éxito! Esto nos dice$4x^{3} -10x^{2} -2x+2=\left(x+\dfrac{1}{2} \right)\left(4x^{2} -12x+4\right)$, y que la gráfica tiene una intercepción horizontal en$x=-\dfrac{1}{2}$.

Para encontrar las dos intercepciones restantes, podemos usar la ecuación cuadrática, estableciendo$4x^{2} -12x+4=0$. Primero, podríamos sacar el factor común,$4\left(x^{2} -3x+1\right)=0$.

\[x=\dfrac{3\pm \sqrt{(-3)^{2} -4(1)(1)} }{2(1)} =\dfrac{3\pm \sqrt{5} }{2} \approx 2.618,\; \; 0.382\nonumber \]

Ejercicio$\PageIndex{2}$

Encuentra los ceros reales de$f(x)=3x^{3} -x^{2} -6x+2$

Contestar

Cauchy's Bound nos dice que los ceros se encuentran en el intervalo$\left[-\dfrac{6}{\left|3\right|} -1,\quad \dfrac{6}{\left|3\right|} +1\right]=[-3,3]$. El teorema de las raíces racionales nos dice que los posibles ceros racionales del polinomio están en la lista $Una gráfica cúbica que cruza el eje x en tres puntos poco claros. El primero está entre negativo 2 y negativo 1, el segundo entre 0 y 1, y el tercero entre 1 y 2.$

\[\left\{\pm \dfrac{1}{1} ,\pm \dfrac{1}{3} ,\pm \dfrac{2}{1} ,\pm \dfrac{2}{3} \right\}=\left\{\pm 1,\pm \dfrac{1}{3} ,\pm 2,\pm \dfrac{2}{3} \right\}\nonumber \]

Mirando una gráfica, el único candidato probable es$\dfrac{1}{3}$

Usando división sintética,

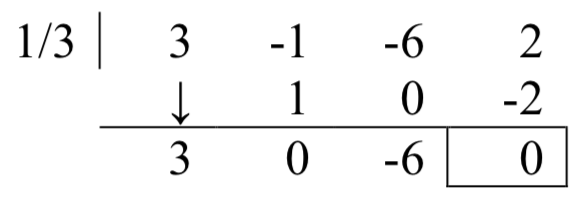
$2019-06-23 8.01.50.png$

\[3x^{3} -x^{2} -6x+2=\left(x-\dfrac{1}{3} \right)\left(3x^{2} -6\right)=3\left(x-\dfrac{1}{3} \right)\left(x^{2} -2\right)\nonumber \]

Resolver$x^{2} -2=0$ da ceros$x=\pm \sqrt{2}$.

Los ceros reales del polinomio son$x=\sqrt{2} ,\; -\sqrt{2} ,\; \dfrac{1}{3}$.

Temas Importantes de esta Sección

Cauchy's Bound para todos los ceros reales de un polinomio
Teorema de raíces racionales
Encontrar ceros reales de un polinomio