9.3: Parábolas y sistemas no lineales

Para escuchar señales desde el espacio, un radiotelescopio utiliza un plato en forma de parábola para enfocar y collec las señales en el receptor.

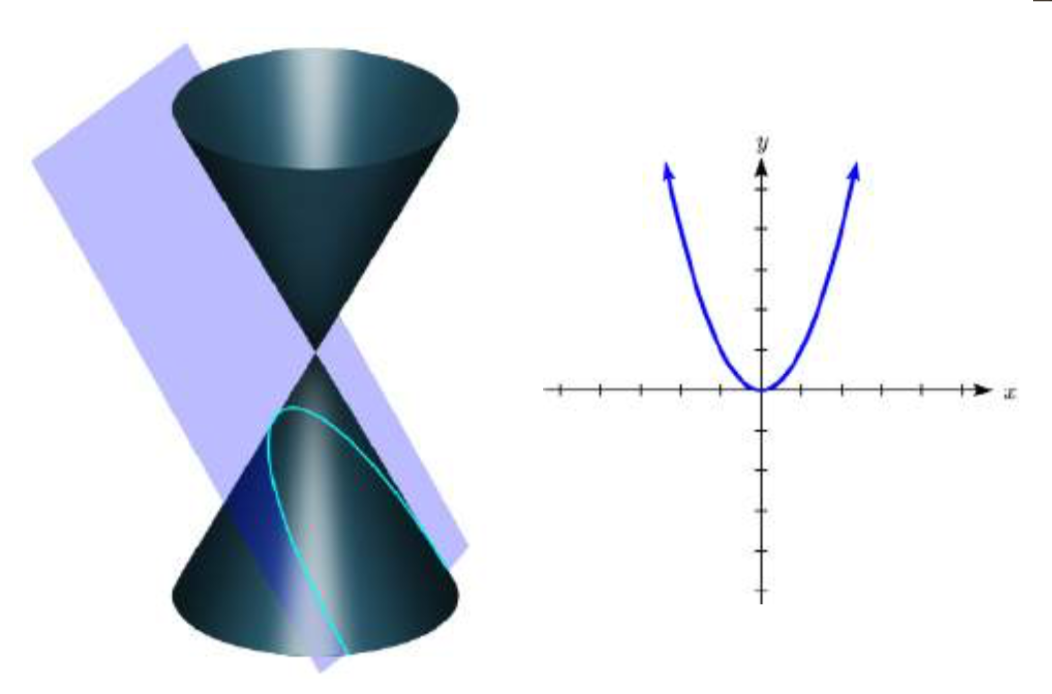
Si bien estudiamos las parábolas antes cuando exploramos las cuadráticas, en ese momento no las discutimos como una sección cónica. Una parábola es la forma resultante de cuando un plano paralelo al lado del cono se cruza con el cono (Pbroks13 (Commons.wikimedia.org/wiki/F... with_plane.svg), “Secciones cónicas con plano”, recortadas para mostrar solo parábola, CC BY 3.0).

Definición: PARÁBOLA Definición Y VOCABULARIO

Una parábola con vértice en el origen se puede definir colocando un punto fijo en\(F\left( 0,p \right)\) llamado foco, y dibujando una línea en\(y = - p\), llamada directriz. La parábola es el conjunto de todos los puntos\(Q\left( x,y \right)\) que están a una distancia igual entre el punto fijo y la directriz.

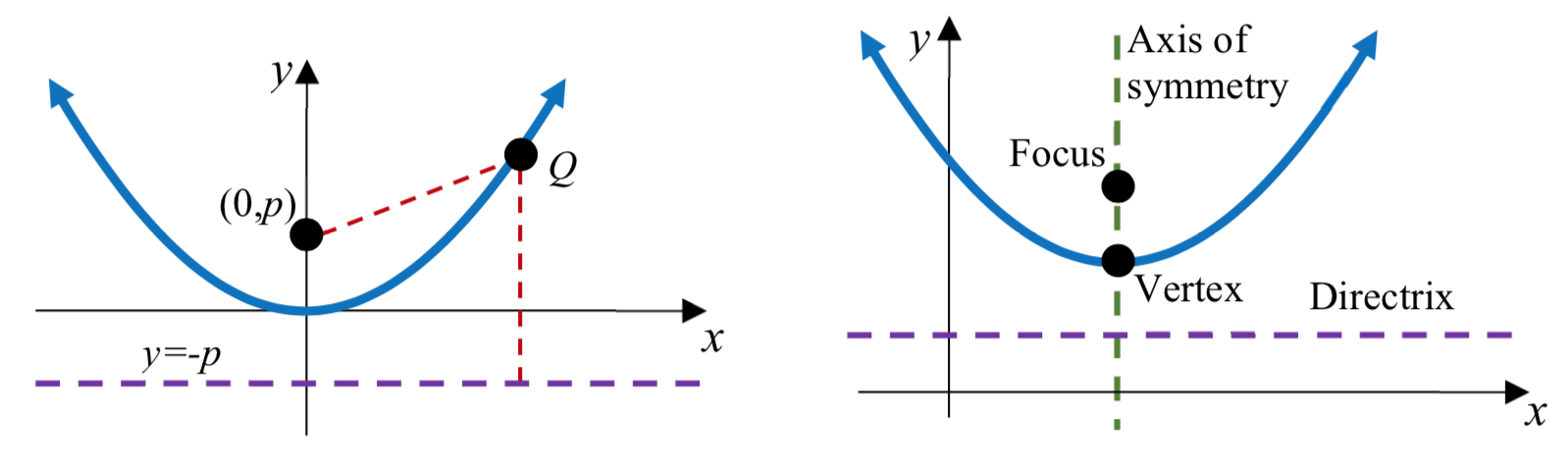
Para las parábolas generales,
El eje de simetría es la línea que pasa por los focos, perpendicular a la directriz.
El vértice es el punto donde la parábola cruza el eje de simetría.
La distancia desde el vértice hasta el foco,\(p\), es la distancia focal.

Ecuaciones para Parábolas con Vértice en el Origen

De la definición anterior podemos encontrar una ecuación de una parábola. Lo encontraremos para una parábola con vértice en el origen,\(C\left( 0,0 \right)\), abriéndose hacia arriba con enfoque en\(F\left( 0,p \right)\) y directriz en\(y = - p\).

Supongamos que\(Q\left( x,y \right)\) es algún punto sobre la parábola. La distancia desde\(Q\) el foco es

\[d(Q,F)=\sqrt{(x-0)^{2}+(y-p)^{2}}=\sqrt{x^{2}+(y-p)^{2}}\nonumber\]

La distancia desde el punto\(Q\) a la directriz es la diferencia de los\(y\) valores -:

\[d = y - ( - p) = y + p\nonumber\]

A partir de la definición de la parábola, estas distancias deben ser iguales:

\[\sqrt {x^2 + \left( y - p \right)^2} = y + p\nonumber\]Cuadrado ambos lados
\[x^2 + \left( y - p \right)^2 = \left( y + p \right)^2\nonumber\] Ampliar
\[x^2 + y^2 - 2py + p^2 = y^2 + 2py +p^2\nonumber\] Combinar términos similares
\[x^2 = 4py\nonumber\]

Esta es la forma cónica estándar de una parábola que se abre hacia arriba o hacia abajo (eje vertical de simetría), centrada en el origen. Tenga en cuenta que si nos dividimos por\(4p\), obtendríamos una ecuación más familiar para la parábola,\(y = \dfrac{x^2}{4p}\). Podemos reconocer esto como una transformación de la parábola\(y = x^2\), comprimida verticalmente o estirada por\(\dfrac{1}{4p}\).

Usando un proceso similar, podríamos encontrar una ecuación de una parábola con vértice en el origen que se abre a la izquierda o a la derecha. El foco estará en (\(p\),0) y la gráfica tendrá un eje horizontal de simetría y una directriz vertical. La forma cónica estándar de su ecuación será\(y^2 = 4px\), que también podríamos escribir como\(x = \dfrac{y^2}{4p}\).

Ejemplo\(\PageIndex{1}\)

Escriba la ecuación cónica estándar para una parábola con vértice en el origen y enfoque en (0, -2).

Solución

Con enfoque en (0, -2), el eje de simetría es vertical, por lo que la ecuación cónica estándar es\(x^2 = 4py\). Dado que el foco es (0, -2),\(p = -2\).

La ecuación cónica estándar para la parábola es\[x^2 = 4( - 2)y\text{, or }x^2 = - 8y\nonumber\]
Para parábolas con vértice no en el origen, podemos desplazar estas ecuaciones, llevando a las ecuaciones resumidas a continuación.

ECUACIÓN DE UNA PARÁBOLA CON VERTEX EN\(h,k\) IN STANDARD CONIC FORM

La forma cónica estándar de una ecuación de una parábola con vértice en el punto\(\left( h,k \right)\) depende de si el eje de simetría es horizontal o vertical. La siguiente tabla da la ecuación estándar, vértice, eje de simetría, directriz, enfoque y gráfica para cada uno.

	Horizontal	Vertical
Ecuación estándar	\((y - k)^2 = 4p(x - h)\)	\((x - h)^2 = 4p(y - k)\)
Vertex	\((h, k)\)	\((h, k)\)
Eje de simetría	\(y = k\)	\(x = h\)
Directrix	\(x = h - p\)	\(y = k - p\)
Foco	\((h +p, k)\)	\((h, k + p)\)
Gráfica	Un ejemplo con\(p < 0\)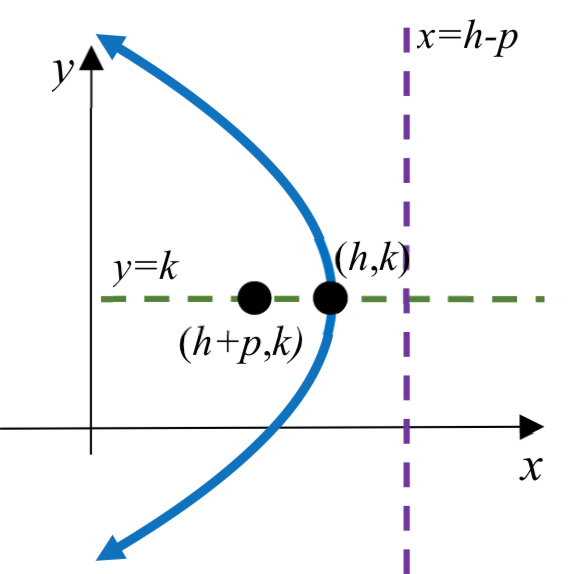	Un ejemplo con\(p > 0\)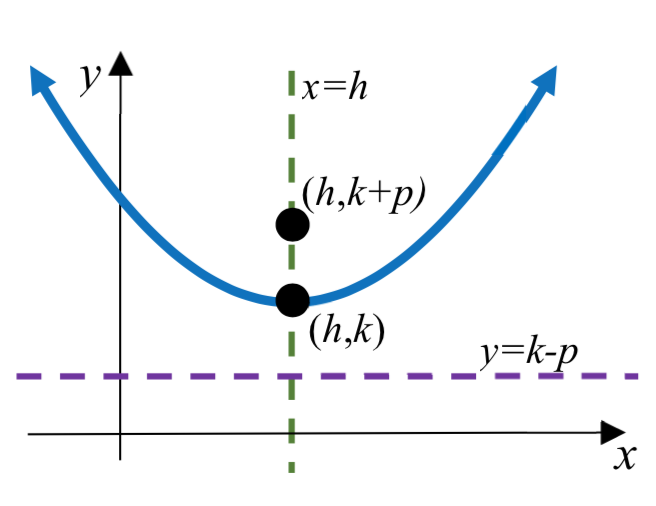

Como ya estudiaste cuadrráticas con cierta profundidad antes, exploraremos principalmente los nuevos conceptos asociados a las parábolas, particularmente el enfoque.

Ejemplo\(\PageIndex{2}\)

Poner la ecuación de la parábola\(y = 8{(x - 1)^2} + 2\) en forma cónica estándar. Encuentra el vértice, el foco y el eje de simetría.

Solución

De tu trabajo anterior con cuadráticas, es posible que ya puedas identificar el vértice como (1,2), pero seguiremos adelante y pondremos la parábola en la forma cónica estándar. Para ello, necesitamos aislar el factor cuadrado.

\[y = 8(x - 1)^2 + 2\nonumber\]Restar 2 de ambos lados
\[y - 2 = 8(x - 1)^2\nonumber\] Dividir por 8
\[\dfrac{\left( y - 2 \right)}{8} = (x - 1)^2\nonumber\]

Esto coincide con la forma general para una parábola vertical,\(\left( x - h \right)^2 = 4p\left( y - k \right)\), dónde\(4p = \dfrac{1}{8}\). Resolver esto nos dice\(p = \dfrac{1}{32}\). La forma cónica estándar de la ecuación es

\[\left( x - 1 \right)^2 = 4\left( \dfrac{1}{32} \right)\left( y - 2 \right). \nonumber\]

El vértice está en (1,2). El eje de simetría está en\(x = 1\).
La directrix está en\[y = 2 - \dfrac{1}{32} = \dfrac{63}{32}\nonumber\]
El foco está en\[\left( 1,2 + \dfrac{1}{32} \right) = \left( 1,\dfrac{65}{32} \right)\nonumber\]

Ejemplo\(\PageIndex{3}\)

Una parábola tiene su vértice en (1, 5) y enfoque en (3, 5). Encuentra una ecuación para la parábola.

Solución

Dado que el vértice y el foco se encuentran en la línea\(y = 5\), ese es nuestro eje de simetría.

El vértice (1, 5) nos dice\(h = 1\) y\(k = 5\).

Mirando la distancia desde el vértice hasta el foco,\(p = 3 – 1 = 2\).

Sustituir estos valores en la forma cónica estándar de una ecuación para una parábola horizontal da la ecuación

\[\left( y - 5 \right)^2 = 4(2)\left( x - 1 \right)\nonumber\]

\[\left( y - 5 \right)^2 = 8\left( x - 1 \right)\nonumber\]

Tenga en cuenta que esto también podría reescribirse resolviendo para\(x\), resultando en

\[x = \dfrac{1}{8}{\left( {y - 5} \right)^2} + 1\nonumber\]

Ejercicio\(\PageIndex{1}\)

Una parábola tiene su vértice en (-2,3) y enfoque en (-2,2). Encuentra una ecuación para esta parábola.

Contestar

El eje de simetría es vertical, y el foco está por debajo del vértice.
\[p = 2 – 3 = -1\nonumber\]
\[\left( x - ( - 2) \right)^2 = 4( - 1)\left( y - 3 \right)\text{, or }\left( x + 2 \right)^2 = - 4\left( y - 3 \right)\nonumber\]

Aplicaciones de Parábolas

En una sección anterior, aprendimos que las elipses tienen una propiedad especial de que un rayo que emana de un foco se reflejará de nuevo al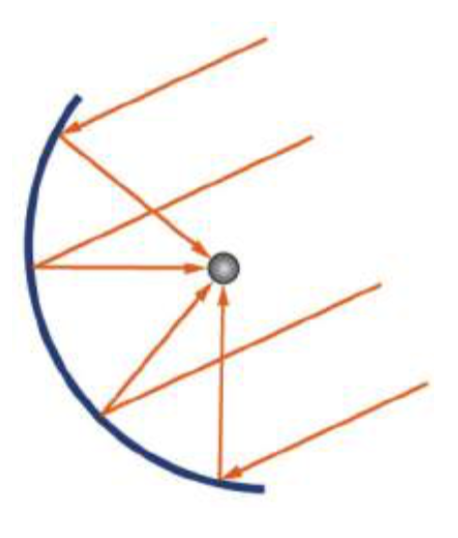 otro foco, la propiedad que permite que la cámara susurrante funcione. Las parábolas también tienen una propiedad especial, que cualquier rayo que emana del foco se reflejará paralelo al eje de simetría. Los reflectores en linternas aprovechan esta propiedad para enfocar la luz de la bombilla en un haz colimado. La misma propiedad se puede utilizar en reversa, tomando rayos paralelos de luz solar o señales de radio y dirigiéndolos todos al foco.

Ejemplo\(\PageIndex{4}\)

Una cocina solar es un plato parabólico que refleja los rayos del sol a un punto central permitiendo cocinar los alimentos. Si una cocina solar tiene un plato parabólico de 16 pulgadas de diámetro y 4 pulgadas de alto, ¿dónde se debe colocar la comida?

Solución

Necesitamos determinar la ubicación del foco, ya que ahí es donde se debe colocar la comida. 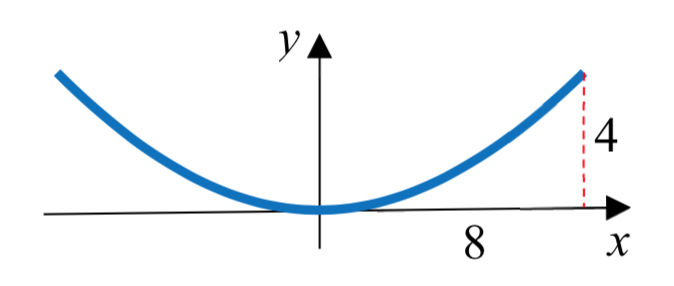Posicionando la base del plato en el origen, la forma desde el lado se ve así:

La forma cónica estándar de una ecuación para la parábola sería\({x^2} = 4py\). La parábola pasa por (4, 8), por lo que sustituyendo eso en la ecuación, podemos resolver por\(p\):

\[8^2 = 4(p)(4)\nonumber\]
\[p = \dfrac{8^2}{16} = 4\nonumber\]

El foco está a 4 pulgadas por encima del vértice. Esto lo convierte en un diseño muy conveniente, ya que entonces se podría colocar una rejilla encima del plato para sostener la comida.

Ejercicio\(\PageIndex{2}\)

Un radiotelescopio tiene 100 metros de diámetro y 20 metros de profundidad. ¿Dónde se debe colocar el receptor?

Contestar

La forma cónica estándar de la ecuación es\[x^2 = 4py\nonumber\]
Usando (50,20), podemos encontrar eso\(50^2 = 4p(20)\), así\(p = 31.25\) metros.
El receptor debe colocarse a 31.25 metros por encima del vértice.

Sistemas no lineales de ecuaciones

En muchas aplicaciones, es necesario resolver para la intersección de dos curvas. Muchas de las técnicas que puede haber usado antes para resolver sistemas de ecuaciones lineales también funcionarán para ecuaciones no lineales, particularmente la sustitución. Ya has resuelto algunos ejemplos de sistemas no lineales cuando encontraste la intersección de una parábola y una línea mientras estudiabas cuadráticas, y cuando encontrabas la intersección de un círculo y una línea mientras estudiabas círculos.

Ejemplo\(\PageIndex{4}\)

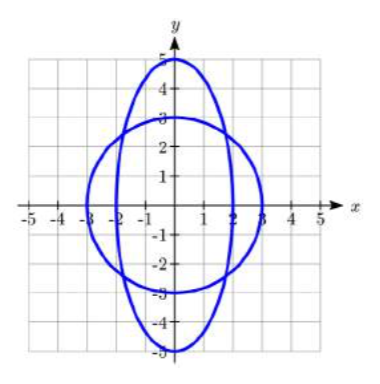
Encuentra los puntos donde la elipse se\(\dfrac{x^2}{4} + \dfrac{y^2}{25} = 1\) cruza con el círculo\(x^2+ y^2 = 9\).

Solución

Para comenzar, podríamos multiplicar la ecuación de elipse por 100 en ambos lados para borrar las fracciones, dando\[25x^2 + 4y^2 = 100\nonumber\]

Un enfoque común para encontrar intersecciones es la sustitución. Con estas ecuaciones, en lugar de resolver para\(x\) o\(y\), podría ser más fácil de resolver para\(x^2\) o\(y^2\). Resolviendo la ecuación circular para\(x^2\) da\(x^2 = 9 - y^2\). Entonces podemos sustituir esa expresión por\(x^2\) en la ecuación de elipse.

\[25x^2 + 4y^2= 100\nonumber\]Sustituto\(x^2 = 9 - y^2\)
\[25\left( 9 - y^2 \right) + 4y^2 = 100\nonumber\] Distribuir
\[225 - 25y^2 + 4y^2 = 100\nonumber\] Combinar términos similares
\[ - 21y^2 = - 125\nonumber\] Dividir por -21
\[y^2 = \dfrac{125}{21}\nonumber\] Usa la raíz cuadrada para resolver
\[y = \pm \sqrt {\dfrac{125}{21}} = \pm \dfrac{5\sqrt 5 }{\sqrt {21} }\nonumber\]

Podemos sustituir cada uno de estos\(y\) valores de nuevo\(x^2 = 9 - y^2\) para encontrar\(x\)

\[x^{2}=9-\left(\sqrt{\frac{125}{21}} \right)^{2}=9-\frac{125}{21}=\frac{189}{21}-\frac{125}{21}=\frac{64}{21}\nonumber\]

\[x = \pm \sqrt {\dfrac{64}{21}} = \pm \dfrac{8}{\sqrt {21} }\nonumber\]

Hay cuatro puntos de intersección:\[\left( \pm \dfrac{8}{\sqrt {21} }, \pm \dfrac{5\sqrt 5 }{\sqrt {21} } \right)\nonumber\]

Vale la pena señalar que hay una segunda técnica que podríamos haber utilizado en el ejemplo anterior, llamada eliminación. Si multiplicamos la ecuación circular por -4 para obtener\( - 4x^2 - 4y^2 = - 36\), entonces podemos agregarla a la ecuación de elipse, eliminando la variable\(y\).

\[25x^2 + 4y^2 = 100\nonumber\]
\[ - 4x^2 - 4y^2 = - 36\nonumber\]Agrega los lados izquierdos y agrega los lados derechos
\[21x^2 = 64\nonumber\] Resolver para\(x\)
\[x = \pm \sqrt {\dfrac{64}{21}} = \pm \dfrac{8}{\sqrt {21} }\nonumber\]

Ejemplo\(\PageIndex{5}\)

Encuentra los puntos donde la hipérbola\(\dfrac{y^2}{4} - \dfrac{x^2}{9} = 1\) se cruza con la parábola\(y = 2x^2\).

Solución

Podemos resolver este sistema de ecuaciones sustituyendo\(y = 2{x^2}\) en la ecuación de hipérbola.

\[\dfrac{(2x^2)^2}{4} - \dfrac{x^2}{9} = 1\nonumber\]
\[\dfrac{4x^4}{4} - \dfrac{x^2}{9} = 1\nonumber\]Simplificar Simplificar y multiplicar por 9
\[9x^4 - x^2 = 9\nonumber\] Mover el 9 a la izquierda
\[9x^4 - x^2 - 9 = 0\nonumber\]

Si bien esto parece un reto de resolver, podemos pensarlo como un “cuadrático disfrazado”, ya que\(x^4 = (x^2)^2\). Dejando\(u = x^2\), la ecuación se convierte

\[9u^2 - u^2 - 9 = 0\nonumber\]Resuelve usando la fórmula cuadrática
\[u = \dfrac{ - ( - 1) \pm \sqrt ( - 1)^2 - 4(9)( - 9) }{2(9)} = \dfrac{1 \pm \sqrt {325} }{18}\nonumber\] Resolver para\(x\)
\[x^2 = \dfrac{1 \pm \sqrt {325} }{18}\nonumber\] Pero\(1 - \sqrt {325} < 0\), así
\[x = \pm \sqrt {\dfrac{1 + \sqrt {325} }{18}} \nonumber\] Esto lleva a dos soluciones reales
\[x \approx 1.028, -1.028\nonumber\]

Sustituyendo estos en\(y = 2{x^2}\), podemos encontrar los valores y correspondientes.
Las curvas se cruzan en los puntos (1.028, 2.114) y (-1.028, 2.114).

Ejercicio\(\PageIndex{3}\)

Encuentra los puntos donde la línea se\(y = 4x\) cruza con la elipse\(\dfrac{y^2}{4} - \dfrac{x^2}{16} = 1\)

Contestar

Sustituyendo\(y = 4x\) da\(\dfrac{\left( 4x \right)^2}{4} - \dfrac{x^2}{16} = 1\).
Simplifica
\[\dfrac{16x^2}{4} - \dfrac{x^2}{16} = 1\nonumber\] Multiplicar por 16 para obtener
\[64x^2 - x^2 = 16\nonumber\]
\[x = \pm \sqrt {\dfrac{16}{63}} = \pm 0.504\nonumber\]

Sustituir esos en\(y = 4x\) da los\(y\) valores correspondientes.
Las curvas se cruzan en (0.504, 2.016) y (-0.504, -2.016).

Resolver la intersección de dos hipérbolas nos permite utilizar el enfoque de navegación LORAN descr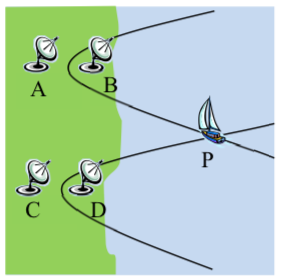 ibed en la última sección.

En nuestro ejemplo, las estaciones A y B están a 150 kilómetros de distancia y envían una señal de radio simultánea al barco. La señal de B llega 0.0003 segundos antes de la señal de A. Encontramos que la ecuación de la hipérbola en forma estándar sería

\[\dfrac{x^2}{2025} - \dfrac{y^2}{3600} = 1\nonumber\]

Ejemplo\(\PageIndex{10}\)

Continuando con la situación desde el último tramo, supongamos que las estaciones C y D se encuentran a 200 km al sur de las estaciones A y B y a 100 km de distancia. La señal de D llega 0.0001 segundos antes de la señal de C, lo que lleva a la ecuación\(\dfrac{x^2}{225} - \dfrac{(y + 200)^2}{2275} = 1\). Encuentra la posición de la nave.

Solución

Para resolver la posición de la embarcación, necesitamos encontrar dónde se cruzan las hipérbolas. Esto significa resolver el sistema de ecuaciones. Para ello, podríamos comenzar resolviendo ambas ecuaciones para\({x^2}\). Con la primera ecuación del ejemplo anterior

\[\dfrac{x^2}{2025} - \dfrac{y^2}{3600} = 1\nonumber\]Mover el\(y\) término a la derecha
\[\dfrac{x^2}{2025} = 1 + \dfrac{y^2}{3600}\nonumber\] Multiplicar ambos lados por 2025
\[x^2 = 2025 + \dfrac{2025y^2}{3600}\nonumber\] Simplificar
\[x^2 = 2025 + \dfrac{9y^2}{16}\nonumber\]

Con la segunda ecuación, repetimos el mismo proceso

\[\dfrac{x^2}{225} - \dfrac{(y + 200)^2}{2275} = 1\nonumber\]Mover el\(y\) término a la derecha y multiplicar por 225
\[x^2 = 225 + \dfrac{225(y + 200)^2}{2275}\nonumber\] Simplificar
\[x^2 = 225 + \dfrac{9(y + 200)^2}{91}\nonumber\]

Ahora establece estas dos expresiones para\(x^2\) iguales entre sí y resuelve.

\[2025 + \dfrac{9y^2}{16} = 225 + \dfrac{9(y + 200)^2}{91}\nonumber\]Restar 225 de ambos lados
\[1800 + \dfrac{9y^2}{16} = \dfrac{9(y + 200)^2}{91}\nonumber\] Dividir por 9
\[200 + \dfrac{y^2}{16} = \dfrac{(y + 200)^2}{91}\nonumber\] Multiplicar ambos lados por\(16 \cdot 91 = 1456\)
\[291200 + 91y^2 = 16(y + 200)^2\nonumber\] Expandir y distribuir
\[291200 + 91y^2 = 16y^2 + 6400y + 640000\nonumber\] Combinar términos similares en un lado
\[75y^2 - 6400y - 348800 = 0\nonumber\] Resolver usando la fórmula cuadrática
\[y = \dfrac{ - ( - 6400) \pm \sqrt {( - 6400)^2 - 4(75)( - 348800)} }{2(75)} \approx 123.11 \text{ km or }-37.78\text{ km}\nonumber\]

Podemos encontrar los\(x\) valores asociados sustituyendo estos\(y\) valores en cualquiera de las ecuaciones de hipérbola. Cuando\(y \approx 123.11\),

\[x^2 \approx 2025 + \dfrac{9(123.11)^2}{16}\nonumber\]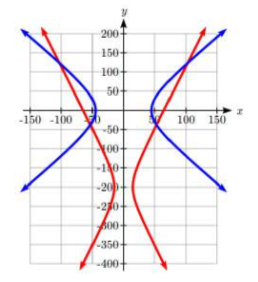
\[x \approx \pm 102.71\nonumber\]

Cuando\(y \approx\) -37.78 km,

\[x^2 \approx 2025 + \dfrac{9( - 37.78)^2}{16}\nonumber\]
\[x \approx \pm 53.18\nonumber\]

Esto proporciona 4 posibles ubicaciones para el barco. Dos pueden ser desechados de inmediato, ya que están en tierra. Los navegantes usarían otras técnicas de navegación para decidir entre las dos ubicaciones restantes.

Temas Importantes de esta Sección

• Definición de parábola
• Ecuaciones de parábola en forma estándar
• Aplicaciones de Parábolas
• Resolviendo Sistemas de Ecuaciones No Lineales