1.1: Ángulos

Última actualización
Guardar como PDF

Page ID: 113536

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Recordemos las siguientes definiciones de geometría elemental:

Un ángulo es agudo si es entre$0°$ y$90°$.
Un ángulo es un ángulo recto si es igual$90°$.
Un ángulo es obtuso si es entre$90°$ y$180°$.
Un ángulo es un ángulo recto si es igual$180°$.

En geometría elemental, los ángulos siempre se consideran positivos y no mayores que$360^\circ $. Por ahora sólo consideraremos tales ángulos. A lo largo del texto se utilizarán las siguientes definiciones:

Dos ángulos agudos son complementarios si su suma es igual$90^◦$. En otras palabras, si$0^◦ ≤ ∠ A , ∠B ≤ 90^◦ \text{ then }∠ A \text{ and }∠B$ son complementarios si$∠ A +∠B = 90^◦$.
Dos ángulos entre ellos$0^◦ \text{ and }180^◦$ son suplementarios si su suma es igual$180^◦$. Es decir, si$0^◦ ≤ ∠ A , ∠B ≤ 180^◦ \text{ then }∠ A \text{ and }∠B$ son suplementarios si$∠ A +∠B = 180^◦$.
Dos ángulos entre ellos$0^◦ \text{ and }360^◦$ son conjugados (o explementarios) si su suma es igual$360^◦$. En otras palabras, si$0^◦ ≤ ∠ A , ∠B ≤ 360^◦ \text{ then }∠ A \text{ and }∠B\text{ are conjugate if }∠ A+∠B = 360^◦$.

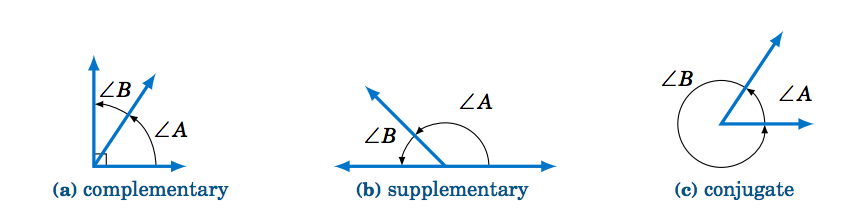
En lugar de usar la notación de ángulo$∠ A$ para denotar un ángulo, a veces usaremos solo una letra mayúscula por sí misma (por ejemplo$A, B, C$) o un nombre de variable en minúscula (por ejemplo$x, y, t$). También es común usar letras (mayúsculas o minúsculas) del alfabeto griego, que se muestran en la tabla siguiente, para representar ángulos:

Tabla 1.1 El alfabeto griego

En geometría elemental aprendiste que la suma de los ángulos en un triángulo es igual$180^◦$, y que un triángulo isósceles es un triángulo con dos lados de igual longitud. Recordemos que en un triángulo rectángulo uno de los ángulos es un ángulo recto. Así, en un triángulo rectángulo es uno de los ángulos$90^◦$ y los otros dos ángulos son ángulos agudos cuya suma es$90^◦$ (es decir, los otros dos ángulos son ángulos complementarios).

Ejemplo 1.1

Para cada triángulo a continuación, determine el ángulo (es) desconocido (s):

Nota: A veces nos referiremos a los ángulos de un triángulo por sus puntos de vértice. Por ejemplo, en el primer triángulo anterior simplemente nos referiremos al ángulo$\angle\,BAC$ como ángulo$A$.

Solución:

Para triángulo$\triangle\,ABC$,$ A = 35^\circ$ y$C = 20^\circ$, y sabemos que$A + B + C = 180^\circ$, por lo

\[\nonumber 35^◦ + B + 20^◦ = 180^◦ ⇒ B = 180^◦ − 35^◦ − 20^◦ ⇒ \fbox{$B = 125^◦$} . \nonumber \]

Para el triángulo rectángulo$△DEF,\, E = 53^◦ \text{ and }F = 90^◦$, y sabemos que los dos ángulos agudos$D$ y$E$ son complementarios, así

\[\nonumber D + E = 90^◦ ⇒ D = 90^◦ − 53^◦ ⇒ \fbox{$D = 37^◦$} . \nonumber \]

Para triángulo$△ XY Z$, los ángulos están en términos de un número desconocido$α$, pero sí lo sabemos$X +Y + Z = 180^◦$, que podemos usar para resolver$α$ y luego usarlo para resolver para$X, Y, \text{ and }Z$:

\[\nonumber α + 3α + α = 180^◦ ⇒ 5α = 180^◦ ⇒ α = 36^◦ ⇒ \fbox{$X = 36^◦ ,\, Y = 3×36^◦ = 108^◦ ,\, Z = 36^◦$} \nonumber \]

Ejemplo 1.2: Teorema de Tales

El Teorema de Thales establece que si$A, \, B,\text{ and }C$ hay puntos (distintos) en un círculo de tal manera que el segmento de línea$\overline{AB}$ es un diámetro del círculo, entonces el ángulo$\angle\,ACB$ es un ángulo recto (ver Figura 1.1.3 (a)). En otras palabras, el triángulo$\triangle\,ABC$ es un triángulo rectángulo.

Figura 1.1.3 Teorema de Tales:$∠ ACB = 90^◦$

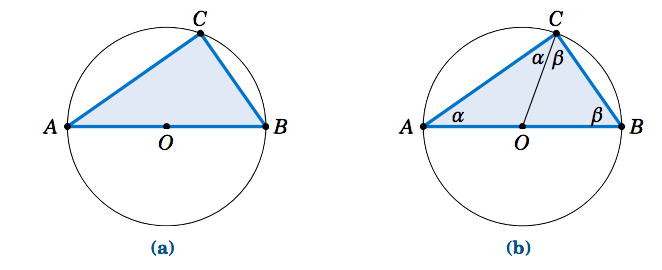
Para probarlo, deje$O$ ser el centro del círculo y dibuje el segmento de línea$\overline{OC}$, como en la Figura 1.1.3 (b). Vamos$α = ∠BAC \text{ and }β = ∠ ABC$. Dado que$\overline{AB}$ es un diámetro del círculo,$\overline{OA} \text{ and }\overline{OC}$ tienen la misma longitud (es decir, el radio del círculo). Esto significa que$△OAC \text{ is an isosceles triangle, and so }∠OCA = ∠OAC = α$. Así mismo,$△OBC$ es un triángulo isósceles y$∠OCB = ∠OBC = β$. Entonces vemos eso$∠ ACB = α+β$. Y como los ángulos de$△ ABC$ deben sumar a$180^◦$, vemos eso$180^◦ = α+(α+β)+β = 2 (α+β), \text{ so }α+β = 90^◦$. Por lo tanto,$∠ ACB = 90^◦$. QED

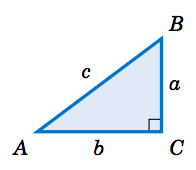
Al conocer las longitudes de dos lados de un triángulo rectángulo, la longitud del tercer lado se puede determinar usando el Teorema de Pitágoras:

Teorema 1.1. Teorema de Pitágoras

El cuadrado de la longitud de la hipotenusa de un triángulo rectángulo es igual a la suma de los cuadrados de las longitudes de sus patas.

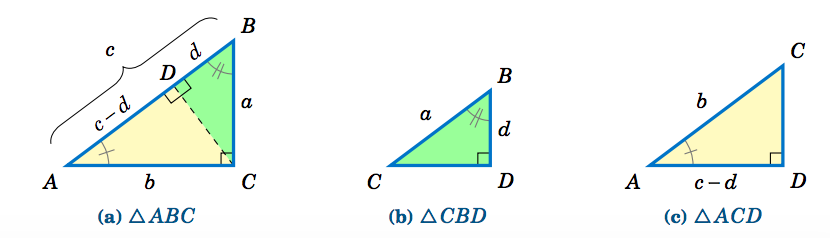
Figura 1.1.5 Triángulos similares$△ ABC, △CBD, △ ACD$

Recordemos que los triángulos son similares si sus ángulos correspondientes son iguales, y esa similitud implica que los lados correspondientes son proporcionales. Así, dado que$\triangle\,ABC $ es similar a$\triangle\,CBD $, por proporcionalidad de lados correspondientes vemos que

\ [\ nonumber\ overline {AB} ~\ text {es a} ~\ overline {CB} ~\ text {(hipotenusas)}\ text {as}
\ overline {BC} ~\ text {es a} ~\ overline {BD} ~\ text {(piernas verticales)}
\ quad\ Rightarrow\ quad\ frac {c} {a} ~=~\ frac {a}} {d}\ quad\ Rightarrow\ quad cd ~=~ a^2 ~. \ nonumber\]

Dado que$\triangle\,ABC $ es similar a$\triangle\,ACD $, comparando piernas horizontales e hipotenusas da

\ [\ nonumber\ frac {b} {c-d} ~=~\ frac {c} {b}\ quad\ Rightarrow\ quad b^2 ~=~ c^2 ~-~ cd ~=~ c ^2 ~-~ a^2
\ quad\ Rightarrow\ quad a^2 ~+~ b^2 ~=~ c^2 ~. \ textbf {QED}\ nonumber\]

Nota: Los símbolos$\perp$ y$\sim$ denotan perpendicularidad y similitud, respectivamente. Por ejemplo, en la prueba anterior tuvimos$\,\overline{CD} \perp \overline{AB}\, $ y$\,\triangle\,ABC \sim \triangle\,CBD \sim \triangle\,ACD $.

Ejemplo 1.3

Para cada triángulo rectángulo a continuación, determine la longitud del lado desconocido:

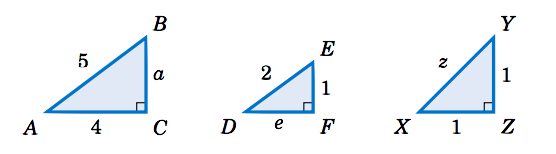
Solución:

Para triángulo$\triangle\,ABC $, el Teorema de Pitágoras dice que

\ [\ nonumber a^2 ~+~ 4^2 ~=~ 5^2\ quad\ Rightarrow\ quad a^2 ~=~ 25 ~-~ 16 ~=~ 9\ quad\ Rightarrow\ quad
\ fbox {$a ~=~ 3$} ~. \ nonumber\]

Para triángulo$\triangle\,DEF $, el Teorema de Pitágoras dice que

\ [\ nonumber e^2 ~+~ 1^2 ~=~ 2^2\ quad\ Rightarrow\ quad e^2 ~=~ 4 ~-~ 1 ~=~ 3\ quad\ Rightarrow\ quad
\ fbox {$e ~=~\ sqrt {3} $} ~. \ nonumber\]

Para triángulo$\triangle\,XYZ $, el Teorema de Pitágoras dice que

\ [\ nonumber 1^2 ~+~ 1^2 ~=~ z^2\ quad\ Rightarrow\ quad z^2 ~=~ 2\ quad\ Rightarrow\ quad
\ quad\ fbox {$z ~=~\ sqrt {2} $} ~. \ nonumber\]

Ejemplo 1.4

Una escalera de 17 pies apoyada contra una pared tiene su pie a 8 pies de la base de la pared. ¿A qué altura está la parte superior de la escalera tocando la pared?

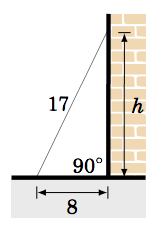
Solución

Deja$h $ ser la altura a la que la escalera toca la pared. Podemos suponer que el suelo hace un ángulo recto con la pared, como en la imagen de la derecha. Luego vemos que la escalera, el suelo y la pared forman un triángulo rectángulo con una hipotenusa de longitud 17 pies (la longitud de la escalera) y patas con longitudes de 8 pies y$h $ pies. Así que por el Teorema de Pitágoras, tenemos

\ [\ nonumber h^2 ~+~ 8^2 ~=~ 17^2\ quad\ Rightarrow\ quad h^2 ~=~ 289 ~-~ 64 ~=~ 225\ quad\ Rightarrow\ quad
\ fbox {$h ~=~ 15 ~\ text {ft} $} ~. \ nonumber\]