1.2: Funciones trigonométricas de un ángulo agudo
- Page ID
- 113520
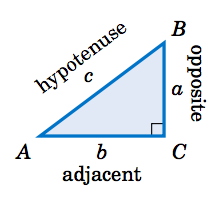
Considera un triángulo rectángulo\(\triangle\,ABC \), con el ángulo recto en\(C \) y con longitudes\(a \)\(b \), y\(c \), como en la figura de la derecha. Para el ángulo agudo\(A\), llame a la pierna\(\overline{BC} \) su lado opuesto, y llame a la pierna\(\overline{AC} \) su lado adyacente. Recordemos que la hipotenusa del triángulo es el lado\(\overline{AB} \). Las proporciones de lados de un triángulo rectángulo ocurren con la suficiente frecuencia en aplicaciones prácticas como para garantizar sus propios nombres, por lo que definimos las seis funciones trigonométricas de la\(A \) siguiente manera:
Cuadro 1.2 Las seis funciones trigonométricas de\(A\)
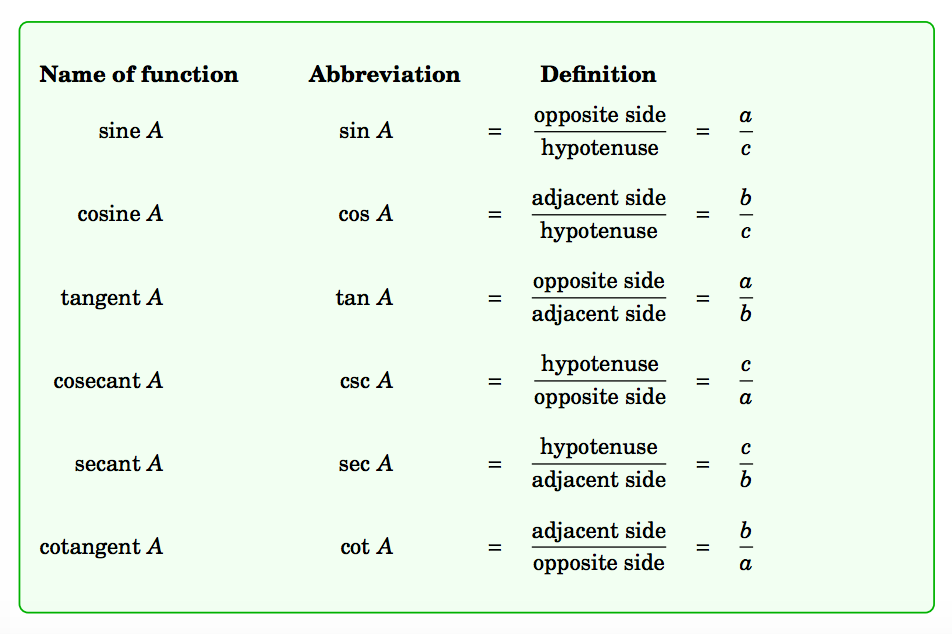
Usualmente usaremos los nombres abreviados de las funciones. Observe de la Tabla 1.2 que los pares\(\sin A \) y\(\csc A \),\(\cos A \) y\(\sec A \), y\(\tan A \) y\(\cot A \) son recíprocos:

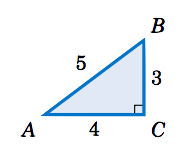
Para el triángulo rectángulo que\(\triangle\,ABC \) se muestra a la derecha, encontrar los valores de las seis funciones trigonométricas de los ángulos agudos\(A \) y\(B \).
Solución:
La hipotenusa de\(\triangle\,ABC \) tiene longitud\(5 \). Para el ángulo\(A \), el lado opuesto\(\overline{BC} \) tiene longitud\(3 \) y el lado adyacente\(\overline{AC} \) tiene longitud\(4 \). Así:
\ [\ nonumber\ sin A ~=~\ dfrac {\ text {opuesto}} {\ texto {hipotenusa}} ~=~\ dfrac {3} {5}\ qquad\ qquad
\ cos A ~=~\ dfrac {\ text {adyacente}} {\ text {hipotenusa}} ~=~\ dfrac {4} {5}\ qquad
\ tan A ~=~\ dfrac {\ text {opuesto}} {\ texto {adyacente}} ~=~\ dfrac {3} {4}\ nonumber\]
\ [\ nonumber\ csc A ~=~\ dfrac {\ text {hipotenusa}} {\ text {opuesto}} ~=~\ dfrac {5} {3}\ qquad\ qquad
\ seg A ~=~\ dfrac {\ text {hipotenusa}} {\ text {adyacente}} ~=~\ dfrac {5} {4}\ qquad\ qquad
\ quad\ cot A ~=~\ dfrac {\ text {adyacente}} {\ text {opuesto}} ~=~\ dfrac {4} {3}\ nonumber\]
Para el ángulo\(B \), el lado opuesto\(\overline{AC} \) tiene longitud\(4 \) y el lado adyacente\(\overline{BC} \) tiene longitud\(3 \). Así:
\ [\ sin B ~=~\ dfrac {\ texto {opuesto}} {\ texto {hipotenusa}} ~=~\ dfrac {4} {5}\ qquad\ qquad
\ cos B ~=~\ dfrac {\ texto {adyacente}} {\ texto {hipotenusa}} ~=~\ dfrac {3} {5}\ qquad\ qquad
\ tan B =~\ dfrac {\ texto {opuesto}} {\ texto {adyacente}} ~=~\ dfrac {4} {3}\ nonumber\]
\ [\ csc B ~=~\ dfrac {\ texto {hipotenusa}} {\ texto {opuesto}} ~=~\ dfrac {5} {4}\ qquad\ qquad
\ seg B ~=~\ dfrac {\ texto {hipotenusa}} {\ texto {adyacente}} ~=~\ dfrac {5} {3}\ qquad\ qquad
\ cuna B ~=~\ dfrac {\ texto {adyacente}} {\ texto {opuesto}} ~=~\ dfrac {3} {4}\ nonumber\]
Observe en el Ejemplo 1.5 que no especificamos las unidades para las longitudes. Esto plantea la posibilidad de que nuestras respuestas dependieran de un triángulo de un tamaño físico específico.
Por ejemplo, supongamos que dos estudiantes diferentes están leyendo este libro de texto: uno en Estados Unidos y otro en Alemania. El estudiante estadounidense piensa que los largos\(3 \),\(4 \), y\(5 \) en el Ejemplo 1.5 se miden en pulgadas, mientras que el estudiante alemán piensa que se miden en centímetros. Ya que\(1 \) en\(\approx \)\(2.54 \) cm, los alumnos están utilizando triángulos de diferentes tamaños físicos (ver Figura 1.2.1 a continuación, no dibujados a escala).
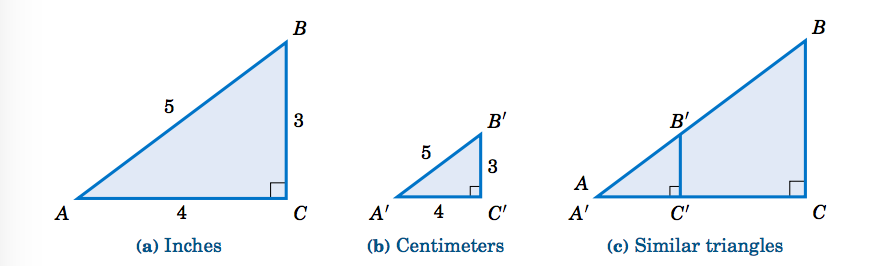
Si el triángulo americano es\(\triangle\,ABC \) y el triángulo alemán lo es\(\triangle\,A'B'C' \), entonces vemos en la Figura 1.2.1 que\(\triangle\,ABC \) es similar a\(\triangle\,A'B'C' \), y de ahí que los ángulos correspondientes son iguales y las proporciones de los lados correspondientes son iguales. De hecho, sabemos esa relación común: los lados de\(\triangle\,ABC \) son aproximadamente\(2.54 \) veces más largos que los lados correspondientes de\(\triangle\,A'B'C' \). Entonces, cuando el estudiante estadounidense calcula\(\sin A \) y el estudiante alemán calcula\(\sin A' \), obtienen la misma respuesta:
\ [\ triángulo\, ABC ~\ sim~\ triángulo\, A'B'C'\ quad\ Rightarrow\ quad
\ dfrac {BC} {B'C'} ~=~\ dfrac {AB} {A'B'}\ quad\ Rightarrow\ quad
\ dfrac {BC} {AB} ~=~\ dfrac {B'C'} {A'B'}\\ Rightarrow\ quad\ sin A ~=~\ sin A'\ nonumber\]
Asimismo, los otros valores de las funciones trigonométricas de\(A \) y\(A'\) son los mismos. De hecho, nuestro argumento fue lo suficientemente general como para trabajar con cualquier triángulo recto similar. Esto nos lleva a la siguiente conclusión:
Al calcular las funciones trigonométricas de un ángulo agudo\(A \), puede usar cualquier triángulo rectángulo que tenga\(A \) como uno de los ángulos.
Dado que definimos las funciones trigonométricas en términos de proporciones de lados, se puede pensar en las unidades de medida para esos lados como canceladas en esas relaciones. Esto significa que los valores de las funciones trigonométricas son números sin unidades. Entonces, cuando el estudiante estadounidense calculó\(3/5 \) como el valor de\(\sin A \) en el Ejemplo 1.5, eso es lo mismo\(3/5 \) que el que calculó el estudiante alemán, a pesar de las diferentes unidades para las longitudes de los lados.
Encuentra los valores de las seis funciones trigonométricas de\(45^\circ \).
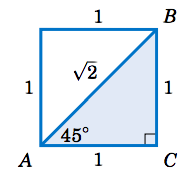
Solución:
Ya que podemos usar cualquier triángulo rectángulo que tenga\(45^\circ \) como uno de los ángulos, utilizar el más simple: tomar un cuadrado cuyos lados son todos\(1 \) unidad de largo y dividirlo por la mitad diagonalmente, como en la figura de la derecha. Dado que las dos patas del triángulo\(\triangle\,ABC \) tienen la misma longitud,\(\triangle\,ABC \) es un triángulo isósceles, lo que significa que los ángulos\(A \) y\(B \) son iguales. Entonces ya\(A + B = 90^\circ \), esto quiere decir que debemos tener\(A = B = 45^\circ \). Según el Teorema de Pitágoras, la longitud\(c \) de la hipotenusa viene dada por
\[c^2 ~=~ 1^2 ~+~ 1^2 ~=~ 2 \quad\Rightarrow\quad c ~=~ \sqrt{2} ~ \nonumber \]
Así, usando el ángulo\(A \) obtenemos:
\ [\ sin\; 45^\ circ ~=~\ dfrac {\ text {opuesto}} {\ texto {hipotenusa}} ~=~\ dfrac {1} {\ sqrt {2}}\ quad\ cuádruple
\ cos\; 45^\ circ ~=~\ dfrac {\ text {adyacente}} {\ text {hipotenusa}} ~=~\ dfrac {1} {\ sqrt {2}}\ quad\ quad
\ tan\; 45^\ circ ~=~\ dfrac {\ text {opuesto}} {\ text {adyacente}} ~=~\ dfrac {1} {1} ~=~ 1\ nonumber\]
\ [\ csc\; 45^\ circ ~=~\ dfrac {\ text {hipotenusa}} {\ text {opuesto}} ~=~\ sqrt {2}\ quad
\ quad\ seg\; 45^\ circ ~=~\ dfrac {\ text {hipotenusa}} {\ text {adyacente}} ~=~\ sqrt {2}\ quad
\ cot\; 45^\ circ ~=~\ dfrac {\ texto {adyacente}} {\ texto {opuesto}} ~=~\ dfrac {1} {1} ~=~ 1\ nonumber\]
Tenga en cuenta que hubiéramos obtenido las mismas respuestas si hubiéramos usado algún triángulo rectángulo similar a\(\triangle\,ABC \). Por ejemplo, si multiplicamos cada lado de\(\triangle\,ABC \) por\(\sqrt{2} \), entonces tendríamos un triángulo similar con patas de longitud\(\sqrt{2} \) e hipotenusa de longitud\(2 \). Esto nos daría\(\sin 45^\circ = \frac{\sqrt{2}}{2} \), que iguala\(\frac{\sqrt{2}}{\sqrt{2} \cdot \sqrt{2}} = \frac{1}{\sqrt{2}} \) como antes. Lo mismo ocurre con las demás funciones.
Encuentra los valores de las seis funciones trigonométricas de\(60^\circ \).
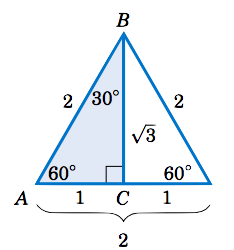
Solución:
Ya que podemos usar cualquier triángulo rectángulo que tenga\(60^\circ \) como uno de los ángulos, usaremos uno simple: tomar un triángulo cuyos lados sean todas las\(2 \) unidades de largo y dividirlo por la mitad dibujando la bisectriz de un vértice al lado opuesto, como en la figura de la derecha. Como el triángulo original era un triángulo equilátero (es decir, los tres lados tenían la misma longitud), sus tres ángulos eran todos iguales, a saber\(60^\circ \). Recordemos de la geometría elemental que la bisectriz desde el ángulo de vértice de un triángulo equilátero hasta su lado opuesto biseca tanto el ángulo del vértice como el lado opuesto. Entonces como en la figura de la derecha, el triángulo\(\triangle\,ABC \) tiene ángulo\(A = 60^\circ \) y ángulo\(B = 30^\circ \), lo que obliga al ángulo\(C \) a ser\(90^\circ \). Así,\(\triangle\,ABC \) es un triángulo rectángulo. Vemos que la hipotenusa tiene longitud\(c = AB = 2 \) y la pierna\(\overline{AC} \) tiene longitud\(b = AC = 1 \). Según el Teorema de Pitágoras, la longitud\(a \) de la pierna\(\overline{BC} \) viene dada por
\ [a^2 ~+~ b^2 ~=~ c^2\ quad\ Rightarrow\ quad a^2 ~=~ 2^2 ~-~ 1^2 ~=~ 3
\ quad\ Rightarrow\ quad a ~=~\ sqrt {3} ~. \ nonumber\]
Así, usando el ángulo\(A \) obtenemos:
\ [\ sin 60^\ circ\; =\;\ dfrac {\ texto {opuesto}} {\ texto {hipotenusa}}\; =\;\ dfrac {\ sqrt {3}} {2}\ qquad
\ cos 60^\ circ\; =\;\ dfrac {\ texto {adyacente}} {\ texto {hipotenusa}}\; =\ dfrac {1} {2}\ qquad
\ tan 60^\ circ\; =\;\ dfrac {\ texto {opuesto}} {\ texto {adyacente}}\; =\;\ dfrac {\ sqrt {3}} {1}\, =\,
\ sqrt {3}\ nonumber\]
\ [\ csc 60^\ circ\; =\;\ dfrac {\ texto {hipotenusa}} {\ texto {opuesto}}\; =\;\ dfrac {2} {\ sqrt {3}}\ qquad
\ seg 60^\ circ\; =\;\ dfrac {\ texto {hipotenusa}} {\ texto {adyacente}}\; =\; 2\ qquad
\ cuna 60^\ circ\; =\;\ dfrac {\ texto {adyacente}} {\ texto {opuesto}}\; =\;
\ dfrac {1} {\ sqrt {3}} ~\ quad\ quad\ nonumber\]
Observe que, como bono, obtenemos los valores de las seis funciones trigonométricas de\(30^\circ \), mediante el uso de ángulo\(B = 30^\circ \) en el mismo triángulo\(\triangle\,ABC \) anterior:
\ [\ sin 30^\ circ\; =\;\ dfrac {\ texto {opuesto}} {\ texto {hipotenusa}}\; =\;\ dfrac {1} {2}\ qquad
\ cos 30^\ circ\; =\;\ dfrac {\ text {adyacente}} {\ text {hipotenusa}}\; =\;\ dfrac {\ sqsq. rt {3}} {2}\ qquad
\ tan 30^\ circ\; =\;\ dfrac {\ texto {opuesto}} {\ texto {adyacente}}\; =\;
\ dfrac {1} {\ sqrt {3}}\ cuádruple\ cuádruple\ nonumber\]
\ [\ csc 30^\ circ\; =\;\ dfrac {\ texto {hipotenusa}} {\ texto {opuesto}}\; =\; =\; 2
\ qquad\ seg 30^\ circ\; =\;\ dfrac {\ texto {hipotenusa}} {\ texto {adyacente}}\; =\;\ dfrac {2} {\ sqrt {3}\ qquad
\ cot 30^\ circ\; =\;\ dfrac {\ texto {adyacente}} {\ texto {opuesto}}\; =\;
\ dfrac {\ sqrt {3}} {1}\; =\; =\; \ sqrt {3}\ nonumber\]
\(A \)es un ángulo agudo tal que\(\sin A = \frac{2}{3} \). Encuentra los valores de las otras funciones trigonométricas de\(A \).
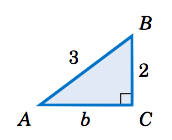
Solución:
En general ayuda a dibujar un triángulo rectángulo para resolver problemas de este tipo. La razón es que las funciones trigonométricas se definieron en términos de proporciones de lados de un triángulo rectángulo, y se le da una de esas funciones (el seno, en este caso) ya en términos de una relación:\(\sin\;A = \frac{2}{3} \). Ya que\(\sin\;A \) se define como\(\frac{\text{opposite}}{\text{hypotenuse}} \), utilizar\(2 \) como la longitud del lado opuesto\(A \) y utilizar\(3 \) como la longitud de la hipotenusa en un triángulo rectángulo\(\triangle\,ABC \) (ver la figura anterior), de manera que\(\sin\;A = \frac{2}{3} \). El lado adyacente a\(A \) tiene longitud desconocida\(b \), pero podemos usar el Teorema de Pitágoras para encontrarlo:
\ [2^2 ~+~ b^2 ~=~ 3^2\ quad\ Rightarrow\ quad b^2 ~=~ 9 ~-~ 4 ~=~ 5\ quad\ Rightarrow\ quad
b ~=~\ sqrt {5}\ nonumber\]
Ahora conocemos las longitudes de todos los lados del triángulo\(\triangle\,ABC \), así que tenemos:
\ [\ cos\; A\; =\;\ dfrac {\ texto {adyacente}} {\ texto {hipotenusa}}\; =\;\ dfrac {\ sqrt {5}} {3}\ qquad
\ tan\; A\; =\;\ dfrac {\ text {opuesto}} {\ text {adyacente}}\; =\;
\ dfrac {2} {\ sqrt {5}}\ quad\ quad\ nonumber\]
\ [\ csc\; A\; =\;\ dfrac {\ texto {hipotenusa}} {\ texto {opuesto}}\; =\;\ dfrac {3} {2}\ qquad
\ seg\; A\; =\; =\;\ dfrac {\ text {hipotenusa}} {\ text {adyacente}}\; =\;\ dfrac {3} {\ sqsqr rt {5}}
\ qquad\ cuna\; A\; =\;\ dfrac {\ texto {adyacente}} {\ texto {opuesto}}\; =\;\ dfrac {\ sqrt {5}} {2}\ nonumber\]
Es posible que hayas notado las conexiones entre el seno y el coseno, secante y cosecante, y tangente y cotangente de los ángulos complementarios en los Ejemplos 1.5 y 1.7. Generalizar esos ejemplos nos da el siguiente teorema:
Si\(A \) y\(B \) son los ángulos agudos complementarios en un triángulo rectángulo\(\triangle\,ABC \), entonces se mantienen las siguientes relaciones:
\[\sin\;A ~=~ \cos\;B \qquad\qquad \sec\;A ~=~ \csc\;B \qquad\qquad \tan\;A ~=~ \cot\;B \nonumber \]
\[\sin\;B ~=~ \cos\;A \qquad\qquad \sec\;B ~=~ \csc\;A \qquad\qquad \tan\;B ~=~ \cot\;A \nonumber \]
Decimos que los pares de funciones\(\lbrace\;\sin, \cos\;\rbrace \),\(\lbrace\;\sec, \csc\;\rbrace \), y\(\lbrace\;\tan, \cot\;\rbrace \) son\(\textbf{cofunctions}\).
Entonces seno y coseno son cofunciones, secante y cosecante son cofunciones, y tangente y cotangente son cofunciones. Así es como las funciones coseno, cosecante y cotangente consiguieron la “co” en sus nombres. El Teorema de la Cofunción dice que cualquier función trigonométrica de un ángulo agudo es igual a su cofunción del ángulo complementario.
Escribe cada uno de los siguientes números como funciones trigonométricas de un ángulo menor que\(45^\circ : \textbf{(a)} \sin\;65^\circ; \textbf{(b)} \cos\;78^\circ; \textbf{(c)} \tan\;59^\circ \).
Solución
\(\textbf{(a)}\)El complemento de\(65^\circ \) es\(90^\circ - 65^\circ = 25^\circ \) y la cofunción de\(\sin \) es\(\cos \), así que por el Teorema de la Cofunción lo sabemos\(\sin\;65^\circ = \cos\;25^\circ \).
\(\textbf{(b)}\)El complemento de\(78^\circ \) es\(90^\circ - 78^\circ = 12^\circ \) y la cofunción de\(\cos \) es\(\sin \), entonces\(\cos\;78^\circ = \sin\;12^\circ \).
\(\textbf{(c)}\)El complemento de\(59^\circ \) es\(90^\circ - 59^\circ = 31^\circ \) y la cofunción de\(\tan \) es\(\cot \), entonces\(\tan\;59^\circ = \cot\;31^\circ \).
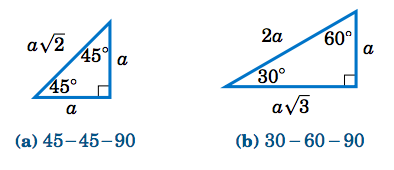
Los ángulos\(30^\circ \),\(45^\circ \), y\(60^\circ \) surgen a menudo en aplicaciones. Podemos usar el Teorema de Pitágoras para generalizar los triángulos rectos en los Ejemplos 1.6 y 1.7 y ver cómo se ven los triángulos cualquiera\(45-45-90 \) y\(30-60-90 \) derecho, como en la Figura 1.2.2 anterior.
Encuentra el seno, coseno, y tangente de\(75^\circ \).
Solución
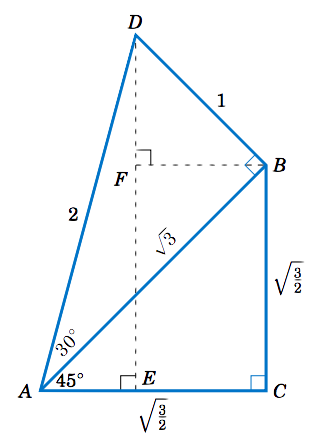
Ya que\(75^\circ = 45^\circ + 30^\circ \), colocar un\(30-60-90 \) triángulo rectángulo\(\triangle\,ADB \) con patas de longitud\(\sqrt{3} \) y\(1 \) encima de la hipotenusa de un\(45-45-90 \) triángulo rectángulo\(\triangle\,ABC \) cuya hipotenusa tiene longitud\(\sqrt{3} \), como en la figura de la derecha. De la Figura 1.2.2 (a) sabemos que la longitud de cada pata de\(\triangle\,ABC\) es la longitud de la hipotenusa dividida por\(\sqrt{2} \). Entonces\(AC = BC = \frac{\sqrt{3}}{\sqrt{2}} =\sqrt{\frac{3}{2}} \). Dibuja\(\overline{DE} \) perpendicular a\(\overline{AC} \), de modo que\(\triangle\,ADE\) sea un triángulo rectángulo. Desde\(\angle\,BAC = 45^\circ \) y\(\angle\,DAB = 30^\circ \), vemos que\(\angle\,DAE = 75^\circ \) ya que es la suma de esos dos ángulos. Por lo tanto, necesitamos encontrar el seno, el coseno y la tangente de\(\angle\,DAE \).
Observe que\(\angle\,ADE = 15^\circ \), ya que es el complemento de\(\angle\,DAE \). Y\(\angle\,ADB = 60^\circ \), ya que es el complemento de\(\angle\,DAB \). Dibuja\(\overline{BF} \) perpendicular a\(\overline{DE} \), de modo que\(\triangle\,DFB \) sea un triángulo rectángulo. Entonces\(\angle\,BDF = 45^\circ \), ya que es la diferencia de\(\angle\,ADB = 60^\circ \) y\(\angle\,ADE = 15^\circ \). También,\(\angle\,DBF = 45^\circ \) ya que es el complemento de\(\angle\,BDF \). La hipotenusa\(\overline{BD} \) de\(\triangle\,DFB \) tiene longitud\(1 \) y\(\triangle\,DFB \) es un\(45-45-90 \) triángulo rectángulo, así que lo sabemos\(DF = FB = \frac{1}{\sqrt{2}} \).
Ahora, eso lo sabemos\(\overline{DE} \perp \overline{AC} \) y\(\overline{BC} \perp \overline{AC} \), así\(\overline{FE} \) y\(\overline{BC} \) son paralelos. Del mismo modo,\(\overline{FB} \) y\(\overline{EC} \) son ambos perpendiculares\(\overline{DE} \) y por lo tanto\(\overline{FB} \) es paralelo a\(\overline{EC} \). Así,\(FBCE \) es un rectángulo, ya que\(\angle\,BCE \) es un ángulo recto. Entonces\(EC = FB = \frac{1}{\sqrt{2}}\) y\(FE = BC = \sqrt{\frac{3}{2}} \). Por lo tanto,
\ [DE ~=~ DF ~+~ FE ~=~\ tfrac {1} {\ sqrt {2}} ~+~\ sqrt {\ tfrac {3} {2}} ~=~\ tfrac {\ sqrt {3} ~+~ 1} {\ sqrt {2}}
\ quad\ text {y}\ quad
EC ~=~ AC ~-~ ~\ sqrt {\ tfrac {3} {2}} ~-~\ tfrac {1} {\ sqrt {2}} ~=~\ tfrac {\ sqrt {3} ~-~ 1} {\ sqrt {2}}
~. ~\ text {Así,}\ nonumber\]
\ [\ sin\; 75^\ circ =\ tfrac {DE} {AD} =\ tfrac {\ frac {\ frac {\ sqrt {3} + 1} {\ sqrt {2}}} {2} =
\ tfrac {\ sqrt {6} +\ sqrt {2}} {4} ~, ~\ cos\; 75^\ circ =\ tfrac {AE} {AD} =
\ tfrac {\ frac {\ sqrt {3} - 1} {\ sqrt {2}}} {2} =\ tfrac {\ sqrt {6} -\ sqrt {2}} {4}
~, ~\ texto {y} ~\ tan\; 75^\ circ =
\ tfrac {DE} {AE} =\ tfrac {\ frac {\ sqrt {3} + 1} {\ sqrt {2}}} {\ frac {\ sqrt {3} - 1} {\ sqrt {2}} =
\ tfrac {\ sqrt {6} +\ sqrt {2}} {\ sqrt {6} -\ sqrt {2}}} ~. \ nonumber\]
Nota: Tomando reciprocidad, obtenemos\(\csc\;75^\circ = \frac{4}{\sqrt{6} + \sqrt{2}} \),\(\sec\;75^\circ = \frac{4}{\sqrt{6} - \sqrt{2}} \), y\(\cot\;75^\circ = \frac{\sqrt{6} - \sqrt{2}}{\sqrt{6} + \sqrt{2}} \).


