3.1: Identidades trigonométricas básicas

Hasta el momento conocemos algunas relaciones entre las funciones trigonométricas. Por ejemplo, conocemos las relaciones recíprocas:

1. \(\csc\;\theta ~=~ \dfrac{1}{\sin\;\theta} \qquad \)cuando\(\sin\;\theta \ne 0\)
2. \(\sec\;\theta ~=~ \dfrac{1}{\cos\;\theta} \qquad \)cuando\(\cos\;\theta \ne 0\)
3. \(\cot\;\theta ~=~ \dfrac{1}{\tan\;\theta} \qquad \)cuando\(\tan\;\theta \) se define y no\(0\)
4. \(\sin\;\theta ~=~ \dfrac{1}{\csc\;\theta} \qquad \)cuando\(\csc\;\theta \) se define y no\(0\)
5. \(\cos\;\theta ~=~ \dfrac{1}{\sec\;\theta} \qquad \)cuando\(\sec\;\theta \) se define y no\(0\)
6. \(\tan\;\theta ~=~ \dfrac{1}{\cot\;\theta} \qquad \)cuando\(\cot\;\theta \) se define y no\(0\)

Observe que cada una de estas ecuaciones es verdadera para todos los ángulos\(\theta \) para los que se definen ambos lados de la ecuación. Dichas ecuaciones se denominan identidades, y en esta sección discutiremos varias identidades trigonométricas, es decir, identidades que involucran las funciones trigonométricas. Estas identidades se utilizan a menudo para simplificar expresiones o ecuaciones complicadas. Por ejemplo, una de las identidades trigonométricas más útiles es la siguiente:

\[ \tan\;\theta ~=~ \frac{\sin\;\theta}{\cos\;\theta} \qquad \text{when } \cos\;\theta \ne 0 \label{3.1} \]

Para acreditar esta identidad, escoja un punto\((x,y) \) en el lado terminal de\(\theta \) una\(r >0 \) distancia del origen, y supongamos que\(\cos\;\theta \ne 0 \). Entonces\(x \ne 0 \) (desde\(\cos\;\theta = \frac{x}{r}\)), entonces por definición

\ [\ frac {\ sin\;\ theta} {\ cos\;\ theta} ~=~\ dfrac {~\ dfrac {y} {r} ~} {~\ dfrac {x} {r} ~} ~=~\ frac {y} {x} ~=~
\ tan\;\ theta ~.
\ nonumber\]

Observe cómo probamos la identidad expandiendo uno de sus lados (\(\frac{\sin\;\theta}{\cos\;\theta}\)) hasta que obtuvimos una expresión que era igual al otro lado (\(\tan\;\theta\)). Esta es probablemente la técnica más común para probar identidades. Tomar recíprocas en la identidad anterior da:

\[ \cot\;\theta ~=~ \frac{\cos\;\theta}{\sin\;\theta} \qquad \text{when } \sin\;\theta \ne 0 \label{3.2} \]

Figura 3.1.1

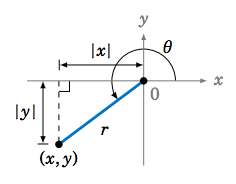
Ahora derivaremos una de las identidades trigonométricas más importantes. Dejar\(\theta \) ser cualquier ángulo con un punto\((x,y) \) en su lado terminal a una\(r>0 \) distancia del origen. Por el Teorema de Pitágoras,\(r^2 = x^2 + y^2 \) (y por lo tanto\(r=\sqrt{x^2 + y^2}\)). Por ejemplo, si\(\theta \) está en QIII como en la Figura 3.1.1, entonces las patas del triángulo rectángulo formado por el ángulo de referencia tienen longitudes\(|x| \) y\(|y| \) (usamos valores absolutos porque\(x \) y\(y \) son negativos en QIII). El mismo argumento se mantiene si\(\theta\) está en los otros cuadrantes o en cualquiera de los ejes. Así,

\ [r^2 ~=~ | {x} |^2 ~+~ | {y} |^2 ~=~ x^2 ~+~ y^2 ~,
\ nonumber\]

así que dividir ambos lados de la ecuación por\(r^2 \) (lo que podemos hacer desde entonces\(r>0\)) da

\ [\ frac {r^2} {r^2} ~=~\ frac {x^2 ~+~ y^2} {r^2} ~=~\ frac {x^2} {r^2} ~+~\ frac {y^2} {r^2} ~=~
\ izquierda (\ frac {x} {r}\ derecha) ^2 ~+~ izquierda\ (\ frac {y} {r}\ derecha) ^2 ~.
\ nonumber\]

Desde\(\frac{r^2}{r^2} = 1 \),\(\frac{x}{r} = \cos\;\theta \), y\(\frac{y}{r} = \sin\;\theta \), podemos reescribir esto como:

\[\cos^2 \;\theta ~+~ \sin^2 \;\theta ~=~ 1 \label{3.3} \]

Se puede pensar en esto como una especie de variante trigonométrica del Teorema de Pitágoras. Tenga en cuenta que usamos la notación\(\sin^2 \;\theta \) para significar\((\sin\;\theta)^2 \), así mismo para el coseno y las otras funciones trigonométricas. Usaremos la misma notación para otros poderes además\(2 \).

De la identidad anterior podemos derivar más identidades. Por ejemplo:

\[ \sin^2 \;\theta ~=~ 1 ~-~ \cos^2 \;\theta \label{3.4} \]

\[ \cos^2 \;\theta ~=~ 1 ~-~ \sin^2 \;\theta \label{3.5} \]

de la que obtenemos (después de tomar raíces cuadradas):

\[ \sin\;\theta ~=~ \pm\,\sqrt{1 ~-~ \cos^2 \;\theta}\label{3.6} \]

\[\cos\;\theta ~=~ \pm\,\sqrt{1 ~-~ \sin^2 \;\theta}\label{3.7} \]

También, a partir de las desigualdades\(0 \le \sin^2 \;\theta = 1 ~-~ \cos^2 \;\theta \le 1 \) y\(0 \le \cos^2 \;\theta = 1 ~-~ \sin^2 \;\theta \le 1 \), tomar raíces cuadradas nos da los siguientes límites en seno y coseno:

\[ -1 ~ \le ~ \sin\;\theta ~ \le ~ 1 \label{3.8} \]

\[-1 ~ \le ~ \cos\;\theta ~ \le ~ 1 \label{3.9} \]

Las desigualdades anteriores no son identidades (ya que no son ecuaciones), sino que proporcionan comprobaciones útiles en los cálculos. Recordemos que derivamos esas desigualdades de las definiciones de seno y coseno en la Sección 1.4.

En la Ecuación\ ref {3.3}, dividiendo ambos lados de la identidad por\(\cos^2 \;\theta \) da

\ [\ frac {\ cos^2\;\ theta} {\ cos^2\;\ theta} ~+~\ frac {\ sin^2\;\ theta} {\ cos^2\;\ theta} ~=~
\ frac {1} {\ cos^2\;\ theta} ~~,
\ nonumber\]

así que desde\(\tan\;\theta = \frac{\sin\;\theta}{\cos\;\theta} \) y\(\sec\;\theta = \frac{1}{\cos\;\theta} \), obtenemos:

\[1 ~+~ \tan^2 \;\theta ~=~ \sec^2 \;\theta \label{3.10} \]

Del mismo modo, dividiendo ambos lados de la Ecuación\ ref {3.3} por\(\sin^2 \;\theta \) da

\ [\ frac {\ cos^2\;\ theta} {\ sin^2\;\ theta} ~+~\ frac {\ sin^2\;\ theta} {\ sin^2\;\ theta} ~=~
\ frac {1} {\ sin^2\;\ theta} ~~,
\ nonumber\]

así que desde\(\cot\;\theta = \frac{\cos\;\theta}{\sin\;\theta} \) y\(\csc\;\theta = \frac{1}{\sin\;\theta} \), obtenemos:

\[\cot^2 \;\theta ~+~ 1 ~=~ \csc^2 \;\theta \label{3.11} \]

Ejemplo 3.1

Simplificar\(\;\cos^2 \;\theta ~ \tan^2 \;\theta\; \).

Solución

Podemos usar la ecuación\ ref {3.5} para simplificar:

\ [\ nonumber\ begin {alinear*}
\ cos^2\;\ theta~\ tan^2\;\ theta ~ &= ~\ cos^2\;\ theta ~\ cdot~
\ frac {\ sin^2\;\ theta} {\ cos^2\;\ theta}\\ noumber
&= ~\ sin^2\;\ theta
\ fin {alinear*}\ nonumber\]

Ejemplo 3.2

Simplificar\(\;5\sin^2 \;\theta ~+~ 4\cos^2 \;\theta\; \).

Solución

Podemos usar la ecuación\ ref {3.1} para simplificar:

\ [\ nonumber\ begin {alinear*}
5\ sin^2\;\ theta ~+~ 4\ cos^2\;\ theta ~ &= ~ 5\ sin^2\;\ theta ~+~
4\ izquierda (1 ~-~\ sin^2\;\ theta\ derecha)\\\ nonumber
&= ~ 5\ sin^2\;\ theta ~+~ 4 ~-~ 4\ sin^2\;\ theta\\ nonumber
&= ~\ sin^2\;\ theta ~+~ 4
\ end {align*}\ nonumber\]

Ejemplo 3.3

\(\;\tan \;\theta ~+~ \cot \;\theta ~=~ \sec \;\theta ~ \csc \;\theta\; \)Demuéstralo.

Solución

Ampliaremos el lado izquierdo y mostraremos que es igual al lado derecho:

\ [\ nonumber\ begin {alignat*} {3}
\ tan\;\ theta +\ cot\;\ theta ~ &= ~\ frac {\ sin\;\ theta} {\ cos\;\ theta} ~+~
\ frac {\ cos\;\ theta} {\ sin\;\ theta} & {}\ qquad &\ text {(por ref\ {3.1} y
\ ref {3.2})}\\\ nonúmero
&= ~\ frac {\ sin\;\ theta} {\ cos\;\ theta }\;\ cdot\;\ frac {\ sin\;\ theta} {\ sin\;\ theta} ~+~
\ frac {\ cos\;\ theta} {\ sin\;\ theta}\;\ cdot\;\ frac {\ cos\;\ theta} {\ cos\;\ theta}
& {}\ qquad &\ text {(ambos multiplican fracciones por\(1\))}\\\ nonumber
&= ~\ frac {\ sin^2\;\ theta ~+~\ cos^2\;\ theta} {\ cos\;\ theta ~\ sin\;\ theta} & {}\ qquad
&\ text {(después de obtener un denominador común)}\\\ nonumber
&= ~\ frac {1} {\ cos\;\ theta ~\ sin\;\ theta} & {}\ qquad &\ text {(por\ ref {3.3})}\\\ nonumber
&= ~\ frac {} {\ cos\;\ theta} ~\ cdot~\ frac {1} {\ sin\;\ theta}\\\ nonumber
&= ~\ sec\;\ theta ~\ csc\;\ theta
\ end {alignat*}\ nonumber\]

En el ejemplo anterior, ¿cómo sabíamos expandir el lado izquierdo en lugar del lado derecho? En general, aunque esta técnica no siempre funciona, es probable que el lado más complicado de la identidad sea más fácil de expandir. El motivo es que, por su complejidad, habrá más cosas que puedas hacer con esa expresión. Por ejemplo, si se le pidió que demuestre que

\ [\ sec\;\ theta ~-~\ sin\;\ theta ~\ tan\;\ theta ~=~\ cos\;\ theta ~,
\ nOnumber\]

no habría mucho de lo que pudieras hacer con el lado derecho de esa identidad; consiste en un solo término (\(\cos\;\theta\)) que no ofrece medios obvios de expansión.

Ejemplo 3.4

\(\;\dfrac{1 ~+~ \cot^2 \;\theta}{\sec\;\theta} ~=~ \csc\;\theta ~ \cot\;\theta\; \)Demuéstralo.

Solución

De los dos lados, el lado izquierdo se ve más complicado, por lo que ampliaremos eso:

\ [\ nonumber\ begin {alignat*} {3}
\ frac {1 ~+~\ cot^2\;\ theta} {\ sec\;\ theta} ~ &= ~\ frac {\ csc^2\;\ theta} {\ seg\;\ theta}
& {}\ qquad &\ text {(por\ ref {3.11})}\\ nonúmero
&= ~\ dfrac {\ csc\;\ theta ~\ cdot~\ dfrac {1} {\ sin\;\ theta}} {\ dfrac {1} {\ cos\;\ theta}} & ; {}
& {}\\ [2mm]\ nonúmero
&= ~\ csc\;\ theta ~\ cdot~\ frac {\ cos\;\ theta} {\ sin\;\ theta} & {} & {}\\\ nonúmero
&= ~\ csc\;\ theta ~\ cot\;\ theta & {}\ qquad &\ text {(por\ ref {3.2})}
\ end {alignat*}\ nonumber\]

Al intentar probar una identidad donde al menos un lado es una proporción de expresiones, la multiplicación cruzada puede ser una técnica efectiva:

\ [\ frac {a} {b} ~=~\ frac {c} {d}\ quad\ texto {si y solo si}\ quad ad ~=~ bc
\ nonumber\]

Ejemplo 3.6

\(\;\dfrac{1 ~+~ \sin\;\theta}{\cos\;\theta} ~=~ \dfrac{\cos\;\theta}{1 ~-~ \sin\;\theta}\; \)Demuéstralo.

Solución

Multiplicar y reducir ambos lados hasta que quede claro que son iguales:

\ [\ nonumber\ begin {alinear*}
(1 ~+~\ sin\;\ theta) (1 ~-~\ sin\;\ theta) ~ &= ~\ cos\;\ theta ~\ cdot~\ cos\;\ theta\;\ nonumber
1 ~-~\ sin^2\;\ theta ~ &= ~\ cos^2\;\ theta
\ fin {alinear*}\ nonumber\]

Por\ ref {3.5} ambos lados de la última ecuación son realmente iguales. Así, la identidad original se mantiene.

Ejemplo 3.7

Supongamos que\(\;a\,\cos\;\theta = b\; \) y\(\;c\,\sin\;\theta = d\; \) para algún ángulo\(\theta \) y algunas constantes\(a \),\(b \),\(c \), y\(d \). \(\;a^2 c^2 = b^2 c^2 + a^2 d^2 \)Demuéstralo.

Solución

Multiplique ambos lados de la primera ecuación por\(c \) y la segunda ecuación por\(a\):

\ [\ nonumber\ begin {align*}
ac\,\ cos\;\ theta ~ &= ~ bc\\ nonumber
ac\,\ sin\;\ theta ~ &= ~ ad
\ end {align*}\ nonumber\]

Ahora cuadre cada una de las ecuaciones anteriores y luego agréguelas juntas para obtener:

\ [\ nonumber\ begin {align*}
(ac\,\ cos\;\ theta) ^2 ~+~ (ac\,\ sin\;\ theta) ^2 ~ &= ~ (bc) ^2 ~+~ (ad) ^2\\ nonumber
(ac) ^2\ left (\ cos^2\;\ theta ~+~\ sin^2\; theta eta\ derecha) ~ &= ~ b^2 c^2 ~+~ a^2 d^2\\ no número
a^2 c^2 ~ &= ~ b^2 c^2 ~+~ a^2 d^2\ qquad\ texto {(por \ ref {3.3})}
\ end {align*}\ nonumber\]

Observe cómo\(\theta \) no aparece en nuestro resultado final. El truco era obtener un coeficiente común (\(ac\)) para\(\;\cos\;\theta\; \) y para que\(\;\sin\;\theta\; \) pudiéramos usar\(\;\cos^2 \;\theta + \sin^2 \;\theta = 1 \). Esta es una técnica común para eliminar funciones trigonométricas de sistemas de ecuaciones.