3.2: Fórmulas de suma y diferencia

Ahora derivaremos identidades para las funciones trigonométricas de la suma y diferencia de dos ángulos. Para la suma de dos ángulos cualquiera\(A \) y\(B \), tenemos las fórmulas de suma:

\[\sin\;(A+B) ~=~ \sin\;A ~ \cos\;B ~+~ \cos\;A ~ \sin\;B\label{eqn:sumsin} \]

\[ \cos\;(A+B) ~=~ \cos\;A ~ \cos\;B ~-~ \sin\;A ~ \sin\;B\label{eqn:sumcos} \]

Para probarlos, primero asumamos que\(A \) y\(B \) son ángulos agudos. Entonces\(A+B \) es agudo u obtuso, como en la Figura 3.2.1. Obsérvese en ambos casos que\(\angle\,QPR = A \), desde

\ [\ begin {align*}
\ ángulo\, QPR ~&=~\ ángulo\, QPO -\ ángulo\, OPM ~=~ (90^\ circ - B) -
(90^\ circ - (A+B)) ~=~ A ~~\ text {en la Figura 3.2.1 (a), y}\\ [4pt]
\ ángulo\, QPR ~&=~\ ángulo\, QPO +\ ángulo\, OPM ~=~ (90^\ circ - B) +
(90^\ circ - (180^\ circ - (A+B))) ~= ~ A ~~\ texto {en la Figura 3.2.1 (b).}
\ end {align*}\ nonumber\]

Figura 3.2.1\(\sin (A +B) \text{ and }\cos (A +B)\) para aguda\(A\) y\(B\)

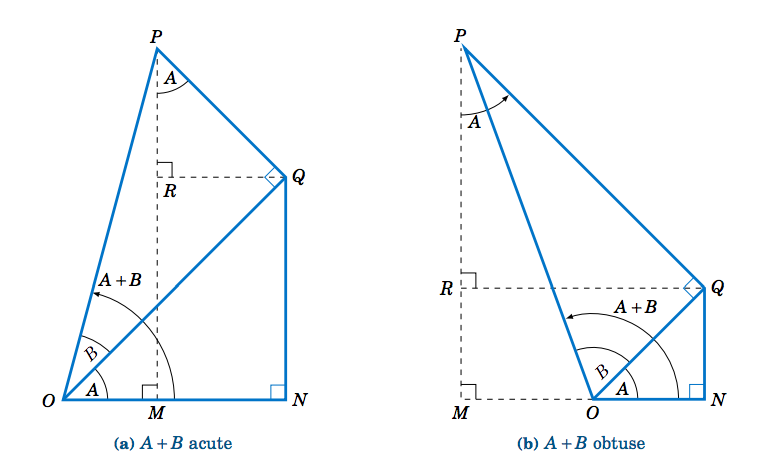
Por lo tanto,

\ [\ begin {alinear*}
\ sin\ ;( A+B) ~&=~\ frac {MP} {OP} ~=~\ frac {MR+RP} {OP} ~=~\ frac {NQ+RP} {OP} ~=~
\ frac {NQ} {OP} ~+~\ frac {RP} {OP}\\ [4pt]
&=~\ frac ac {NQ} {OQ}\,\ cdot\,\ frac {OQ} {OP} ~+~\ frac {RP} {PQ}\,\ cdot\,\ frac {PQ} {OP}\ nonumber\\ [4pt]
&=~\ sin\; A ~\ cos\; B ~+~\ cos\; A ~\ sin\; B ~,\ etiqueta {eqn:sinsumproof}
\ end {align*}\ nonumber\]

y

\ [\ begin {alinear*}
\ cos\ ;( A+B) ~&=~\ frac {OM} {OP} ~=~\ frac {ON-MN} {OP} ~=~\ frac {ON-RQ} {OP} ~=~
\ frac {ON} {OP} ~-~\ frac {RQ} {OP}\\ [4pt]
&=~\ frac {ON} {OQ}\,\ cdot\,\ frac {OQ} {OP} ~-~\ frac {RQ} {PQ}\,\ cdot\,\ frac {PQ} {OP}\\ [4pt]
&=~\ cos\; A ~\ cos\ ; B ~-~\ pecado\; A ~\ pecado\; B ~. \ label {eqn:cossumproof}
\ end {align*}\ nonumber\]

Entonces hemos demostrado las identidades para ángulos agudos\(A \) y\(B \). Es sencillo verificar que sostengan en el caso especial de\(A=B=0^\circ \). Para ángulos generales, necesitaremos usar las relaciones que derivamos en la Sección 1.5 que implican sumar o restar\(90^\circ\):

\ [\ begin {alignat*} {4}
\ sin\ ;(\ theta + 90^\ circ) ~ &= ~\ phantom {-}\ cos\;\ theta &\ qquad\ quad
\ sin\ ;(\ theta - 90^\ circ) ~ &= ~ -\ cos\;\ theta\ [4pt]
\ cos\ ;(\ theta + 90^\ circ) ~ &= ~ -\ sin\;\ theta &\ qquad\ quad
\ cos\ ;(\ theta - 90^\ circ) ~ &= ~\ phantom {-}\ sin\;\ theta
\ end {alignat*}\ nonumber\]

Estos serán útiles porque cualquier ángulo se puede escribir como la suma de un ángulo agudo (o\(0^\circ\)) y múltiplos enteros de\(\pm 90^\circ\). Por ejemplo,\(155^\circ = 65^\circ + 90^\circ \),\(222^\circ = 42^\circ + 2(90^\circ) \),\(-77^\circ = 13^\circ - 90^\circ \), etc. entonces si podemos probar que las identidades se mantienen al sumar o restar\(90^\circ \) a o de cualquiera\(A\) o\(B \), respectivamente, donde\(A \) y\(B \) son agudas o\(0^\circ \), entonces las identidades también se mantendrán cuando sumar o restar repetidamente\(90^\circ \), y por lo tanto se mantendrá para todos los ángulos. Reemplazar\(A \) por\(A+90^\circ \) y usar las relaciones para agregar\(90^\circ \) da

\ [\ begin {alinear*}
\ sin\ ;( (A+90^\ circ) + B) ~&=~\ sin\ ;( (A+B) + 90^\ circ) ~=~\ cos\ ;( A+B) ~,\\ [4pt]
&=~\ cos\; A ~\ cos\; B ~-~\ sin\; A ~\ sin\; B ~\ text {(por Ecuación\ ref {eqn:cossumproof})}\\ [4pt]
&=~\ sin\ ;( A + 90^\ circ) ~\ cos\; B ~+~\ cos\ ;( A + 90^\ circ) ~\ sin\ ; B ~,\ final {alinear*}\ nonumber\]

por lo que la identidad se mantiene para\(A+90^\circ \) y\(B \) (y, de manera similar, para\(A \) y\(B+90^\circ\)). Asimismo,

\ [\ nonumber\ begin {align*}\ sin\; ((A-90^\ circ) + B) ~&=~\ sin\; ((A+B) - 90^\ circ) ~=~ -\ cos\; (A+B) ~,\\ [4pt]
&=~ - (\ cos\; A ~\ cos\; B ~-~\ sin\; A\ sin\; B)\\ [4pt]
&=~ (-\ cos\; A) ~\ cos\; B ~+~\ sin\; A ~\ sin\; B\\ [4pt]
&=~\ sin\ ;( A - 90^\ circ) ~\ cos\; B ~+ ~\ cos\; (A - 90^\ circ) ~\ sin\; B ~,
\ final {alinear*}\ nonumber\]

por lo que la identidad se mantiene para\(A-90^\circ \) y\(B \) (y, de manera similar, para\(A \) y\(B+90^\circ\)). Así, la ecuación de suma\ ref {eqn:sumsin} para seno se mantiene para todos\(A \) y\(B \). Un argumento similar muestra que la ecuación de suma\ ref {eqn:sumcos} para coseno es verdadera para todos\(A \) y\(B \). QED

Sustituir\(B \) por\(-B \) en las fórmulas de suma y usar las relaciones\(\sin\;(-\theta) = -\sin\;\theta \) y\(\cos\;(-\theta) = \cos\;\theta \) de la Sección 1.5 nos da las fórmulas de resta:

\[ \sin\;(A-B) ~=~ \sin\;A ~ \cos\;B ~-~ \cos\;A ~ \sin\;B\label{eqn:diffsin} \]

\[ \cos\;(A-B) ~=~ \cos\;A ~ \cos\;B ~+~ \sin\;A ~ \sin\;B\label{eqn:diffcos} \]

Usando la identidad\(\tan\;\theta = \frac{\sin\;\theta}{\cos\;\theta} \), y las fórmulas de adición para seno y coseno, podemos derivar la fórmula de adición para tangente:

\ [\ requieren {cancelar}\ comenzar {alinear*}
\ tan\ ;( A+B) ~&=~\ frac {\ sin\ ;( A+B)} {\ cos\ ;( A+B)}\\ [4pt]
&=~\ frac {\ sin\; A ~\ cos\; B ~+~\ cos\; A ~\ sin\; B} {\ cos\; A\ cos\; B ~-~\ sin\; A ~\ sin\; B}\\ [4pt]
&=~\ frac {\ dfrac {\ sin\; A ~\ cos\; B} {\ cos\; A ~\ cos\; B} ~+~
\ dfrac {\ cos\; A ~\ sin\; B} {\ cos\; A ~\ cos\; B}} {\ dfrac {\ cos\; A ~\ cos\; B} {\ cos\; A ~\ cos\; B}
~-~\ dfrac {\ sin\; A ~\ sin\; B} {\ cos\; A ~\ cos\; B}}}\ quad\ text {(dividir arriba e abajo por
\(\cos\;A ~ \cos\;B\))}\\ [4pt]
&=~\ frac {\ dfrac {\ sin\; A} {\ cos\; A}\;\ cdot\;\ cancelar {\ dfrac {\ cos\; B} {\ cos\; B}} ~+~
\ cancelar {\ dfrac {\ cos\; A} {\ cos\; A}}\;\ cdot\;\ dfrac {\ sin\; B} {\ cos\; B}} {1 ~-~
\ dfrac {\ sin\; A} {\ cos\; A}}\;\ cdot\;\ dfrac {\ sin\; B} {\ cos\; B}}\\ [4pt]
&=~\ frac {\ tan\; A ~+~\ tan\; B} {1 ~-~\ tan\; A ~\ tan\; B}
\ end {alinear *}\ nonumber\]

Esto, combinado con reemplazar\(B \) por\(-B \) y usar la relación\(\tan\;(-\theta) = -\tan\;\theta \), nos da las fórmulas de suma y resta para tangente:

\[ \tan\;(A+B) ~=~ \frac{\tan\;A ~+~ \tan\;B}{1 ~-~ \tan\;A ~ \tan\;B}\label{eqn:sumtan} \]

\[\tan\;(A-B) ~=~ \frac{\tan\;A ~-~ \tan\;B}{1 ~+~ \tan\;A ~ \tan\;B}\label{eqn:difftan} \]

Ejemplo 3.8

Dados ángulos\(A \) y\(B \) tal que\(\sin\;A = \frac{4}{5} \)\(\cos\;A = \frac{3}{5} \),\(\sin\;B = \frac{12}{13} \),, y\(\cos\;B = \frac{5}{13} \), encontrar los valores exactos de\(\sin\;(A+B) \),\(\cos\;(A+B) \), y\(\tan\;(A+B) \).

Solución

Usando la fórmula de adición para seno, obtenemos:

\ [\ begin {alinear*}
\ sin\ ;( A+B) ~&=~\ sin\; A ~\ cos\; B ~+~\ cos\; A ~\ sin\; B\\ [4pt]
&=~\ frac {4} {5}\;\ cdot\;\ frac {5} {13} ~+~\ frac {3} {5}\;\ cdot\;\ frac {12} {13}
\ quad\ Rightarrow\ quad\ en caja {\ sin\ ;( A+B) ~=~\ frac {56} {65}}\ end {align*}\ nonumber\]

Usando la fórmula de adición para coseno, obtenemos:

\ [\ begin {alinear*}\ cos\; (A+B) ~&=~\ cos\; A ~\ cos\; B ~-~\ sin\; A ~\ sin\; B\\ [4pt]
&=~\ frac {3} {5}\;\ cdot\;\ frac {5} {13} ~-~\ frac {4} {5}\;\ cdot\;\ frac {12} {13}
\ quad\ Rightarrow\ quad\ en caja {\ cos\ ;( A+B) ~=~ -\ frac {33} {65}}\ end {align*}\ nonumber\]

En lugar de usar la fórmula de adición para tangente, podemos usar los resultados anteriores:

\ [\ tan\; (A+B) ~=~\ frac {\ sin\; (A+B)} {\ cos\; (A+B)}
~=~\ frac {\ frac {56} {65}} {-\ frac {33} {65}}
\ quad\ Rightarrow\ quad\ box {\ tan\ ;( A+B) ~=~ -\ frac {56} {33}}\ nonúmero\]

Ejemplo 3.9

Demostrar la siguiente identidad:

\ [\ sin\; (A+B+C) ~=~\ sin\; A~\ cos\; B~\ cos\; C\; +\;\ cos\; A~\ sin\; B~\ cos\; C\; +
\;\ cos\; A~\ cos\; B~\ sin\; C\; -\ sin\; A~\ sin\; B~\ sin\; C\ nonúmero\]

Solución

Trate\(A+B+C \) como\((A+B)+C \) y use las fórmulas de adición tres veces:

\ [\ comenzar {alinear*}
\ sin\ ;( A+B+C) ~&=~\ sin\; ((A+B) +C)\\ [4pt]
&=~\ sin\ ;( A+B) ~\ cos\; C\; +\;\ cos\ ;( A+B) ~\ sin\; C\ [4pt]
&=~ (\ sin\; A ~\ cos\; B\; +\;\ cos\; A ~\ sin\; B) ~\ cos\; C\; +\;
(\ cos\; A ~\ cos\; B\; -\;\ sin\; A ~\ sin\; B) ~\ sin\; C\\ [4pt]
&=~\ sin\; A~\ cos\; B~\ cos\; C\; +\;\ cos\; A~\ sin\; B~\ cos\; C\; +\;
\ cos\; A~\ cos\; B~\ sin\; C\; -\ sin\; A~\ sin\; B~\ sin\; C
\ final {alineación*}\ umber\]

Ejemplo 3.10

Para cualquier triángulo\(\triangle\,ABC \), mostrar que\ (\ tan\; A +\ tan\; B +\ tan\; C =
\ tan\; A~\ tan\; B~\ tan\; C\).

Solución

Tenga en cuenta que esta no es una identidad que se mantenga para todos los ángulos; ya que\(A \)\(B \),, y\(C \) son los ángulos de un triángulo, se sostiene cuando\(A \),\(B \),\(C\)\(> 0^\circ \) y\(A + B + C = 180^\circ \). Entonces usando\(C = 180^\circ - (A+B) \) y la relación\(\;\tan\;(180^\circ - \theta) = -\tan\;\theta\; \) de la Sección 1.5, obtenemos:

\ [\ comenzar {alinear*}\ tan\; A\; +\;\ tan\; B\; +\;\ tan\; C ~&=~\ tan\; A\; +\;\ tan\; B\; +\;\ tan\; (180^\ circ - (A+B))\\ [4pt]
&=~\ tan\; A\; +\; bronceado\\; B\; -\;\ tan\ ;( A+B)\\ [4pt]
&=~\ tan\; A\; +\;\ tan\; B\; -\ frac {\ tan\; A +\ tan\; B} {1 -\ tan\; A ~\ tan\; A ~\ tan\; B}\\ [4pt]
&=~ (\ tan\; A\; +\;\ tan\; B) ~\ izquierda (1\; -\;\ dfrac {1} {1 -\ tan\; A ~\ tan\; B}\ derecha)\\ [4pt]
&=~ (\ tan\; A\; +\;\ tan\; B) ~\ izquierda (\ dfrac {1 bronceado -\\; A ~\ tan\; B} {1 -\ tan\; A ~\ tan\; B}\; -\;
\ dfrac {1} {1 -\ tan\; A ~\ tan\; B}\ derecha)\\ [4pt]
&=~ (\ tan\; A\; + \;\ tan\; B)\;\ cdot\;\ izquierda (\ frac {-\ tan\; A ~\ tan\; B} {1 -\ tan\; A ~\ tan\; B}
\ derecha)\\ [4pt]
&=~\ tan\; A ~\ tan\; B\;\ cdot\;\ cdot\;\ izquierda (-\ frac {\ tan\; A\; +\;\ tan\; B} {1 -\ tan\; A ~\ tan\; B}\ derecha)\\ [4pt]
&=~\ tan\; A ~\ tan\; B\;\ cdot\; (-\ tan\ ;( A+B))\\ [4pt]
&=~\ tan\; A ~\ tan\; B\;\ cdot\; (\ tan\ ;( 180^\ circ - (A+B)))\\ [4pt]
&=~\ tan\; A ~\ tan\; B ~\ tan\; C
\ final {alinear*}\ nonumber\]

Ejemplo 3.11

Dejar\(A \),\(B \),\(C \), y\(D \) ser ángulos positivos tales que\(A+B+C+D=180^\circ \). Demostrar que

\[\sin\;A~\sin\;B ~+~ \sin\;C~\sin\;D ~=~ \sin\;(A+C)~\sin\;(B+C) ~. \nonumber \]

Solución

Puede ser tentador expandir el lado derecho, ya que parece más complicado. No obstante, observe que el lado derecho no tiene\(D \) término. Entonces, en cambio, ampliaremos el lado izquierdo, ya que podemos eliminar el\(D \) término de ese lado usando\(D=180^\circ - (A+B+C) \) y la relación

\[\sin\;(180^\circ -(A+B+C)) ~=~ \sin\;(A+B+C).\nonumber \]

Así que desde\(\;\sin\;D = \sin\;(A+B+C) \), obtenemos

\ [\ begin {alinear*}
\ sin\; A~\ sin\; B ~+~\ sin\; C~\ sin\; D ~&=~\ sin\; A~\ sin\; B ~+~\ sin\; C~\ sin\ ;( A+B+C) ~, ~\ text {así por Ejemplo 3.9 obtenemos}\\ [4pt]
&=~\ sin\; ~\ sin\; B ~+~\ sin\; C~ (\ sin\; A~\ cos\; B~\ cos\; C\; +\;\ cos\; A~\ sin\; B~\ cos\; C\\ [4pt]
&\ quad +\;\ cos\; A~\ cos\; A~\ cos\ cos\; B~\ sin\; C\; -\;\ sin\; A~\ sin\; B~\ sin\; C)\\ [4pt]
&=~\ sin\; A~\ sin\; B ~+~\ sin\; C~\ sin\; A~\ cos\; B~\ cos\; C ~+~\ sin\; C~\ cos\; A~\ sin\; B~\ cos\; C\\ [4pt]
&\ quad +~\ sin\; C~\ cos\; A~\ cos\; B~\ sin\; C ~-~
\ sin\; C~\ sin\; A~\ sin\; B~\ sin\; C ~. \ end {align*}\ nonumber\]

Puede que no sea inmediatamente obvio a dónde ir a partir de aquí, pero no son completamente conjeturas. Tenemos que terminar con\(\sin\;(A+C)~\sin\;(B+C) \), y eso lo sabemos\(\sin\;(B+C) = \sin\;B~\cos\;C + \cos\;B~\sin\;C \). Hay dos términos que involucran\(\;\cos\;B~\sin\;C \), así que agruparlos para obtener

\ [\ comenzar {alinear*}\ sin\; A~\ sin\; B ~+~\ sin\; C~\ sin\; D ~
&=~\ sin\; A~\ sin\; B ~-~\ sin\; C~\ sin\; A~\ sin\; B~\ sin\; C ~+~\ sin\; C~\ cos\; A~\ sin\; ~\ cos\; C\\ [4pt]
&\ cuádruple +~\ cos\; B~\ sin\; C~ (\ sin\; A~\ cos\; C ~+~\ cos\; A~\ sin\; C)\\ [4pt]
&=~\ sin\; A~\ sin\; B~ (1 -\ sin^2 \; C) ~+~\ sin\; C~\ cos\; A~\ sin\; B~\ cos\; C\\ [4pt]
&\ quad +~\ cos\; B~\ sin\; C~\ sin\ ;( A+C)\\ [4pt]
&=~\ sin\; A~\ sin\; B~\ cos^2\; C ~+~ pecado\\; C~\ cos\; A~\ sin\; B~\ cos\; C\\ [4pt]
&\ quad +~\ cos\; B~\ sin\; C~\ sin\ ;( A+C) ~. \ end {align*}\ nonumber\]

Ahora tenemos dos términos que involucran\(\;\sin\;B~\cos\;C \), que podemos facturar:

\ [\ begin {alinear*}\ sin\; A~\ sin\; B ~+~\ sin\; C~\ sin\; D ~&=~\ sin\; B~\ cos\; C~ (\ sin\; A~\ cos\; C +\ cos\; A~\ sin\; C~)\\ [4pt]
&\ quad +~\ cos\; B~\ sin\\; C~\ sin\ ;( A+C)\\[4pt] &=~ \sin\;B~\cos\;C~\sin\;(A+C) ~+~ \cos\;B~\sin\;C~\sin\;(A+C)\\[4pt] &=~ \sin\;(A+C)~(\sin\;B~\cos\;C + \cos\;B~\sin\;C)\\[4pt] &=~ \sin\;(A+C)~\sin\;(B+C) \\[4pt]\end{align*} \nonumber \]

Ejemplo 3.12

En el estudio de la propagación de ondas electromagnéticas, la ley de Snell da la relación

\[n_1 ~\sin\;\theta_1 ~=~ n_2 ~\sin\;\theta_2\label{eqn:snell} ~, \]

donde\(\theta_1 \) es el ángulo de incidencia en el que una ola golpea el límite plano entre dos medios,\(\theta_2 \) es el ángulo de transmisión de la onda a través del nuevo medio,\(n_1 \) y y\(n_2\) son los índices de refracción de los dos medios. La cantidad

\ [r_ {1\; 2\; s} ~=~\ frac {n_1 ~\ cos\;\ theta_1 ~-~ n_2 ~\ cos\;\ theta_2} {n_1 ~\ cos\;\ theta_1 ~+~
n_2 ~\ cos\;\ theta_2}\ label {3.21}\]

se denomina coeficiente de Fresnel para la reflexión de incidencia normal de la onda para polarización s. Demostrar que esto puede escribirse como:

\[ r_{1\;2\;s} ~=~ \frac{\sin\;(\theta_2 - \theta_1)}{\sin\;(\theta_2 + \theta_1)} \nonumber \]

Solución

Multiplica la parte superior e inferior de\(r_{1\;2\;s} \) por\(\;\sin\;\theta_1 ~ \sin\;\theta_2\; \) para obtener:

\ [\ begin {alinear*}
r_ {1\; 2\; s} ~&=~\ frac {n_1 ~\ cos\;\ theta_1 ~-~ n_2 ~\ cos\;\ theta_2} {n_1 ~\ cos\;\ theta_1 ~+~
n_2 ~\ cos\;\ theta_2}\;\ cdot\; frac {\ sin\;\ theta_1 ~\ sin\;\ theta_2} {\ sin\;\ theta_1 ~
\ sin\;\ theta_2}\\ [4pt]
&=~\ frac {(n_1 ~\ sin\;\ theta_1) ~\ sin\;\ theta_2 ~\ cos\;\ theta_1 ~-~
(n_2 ~\ sin\;\ theta_2) ~\ cos\;\ theta_2 ~\ sin\;\ theta_1} {
(n_1 ~\ sin\;\ theta_1) ~\ sin\;\ theta_2 ~\ cos\;\ theta_1 ~+~
(n_2 ~\ sin\;\ theta_2) ~\ cos\;\ theta_2 ~\ sin\;\ theta_1}\\ [4pt]
&=~\ frac {(n_1 ~\ sin\;\ theta_1) ~\ sin\;\ theta_2 ~\ cos\;\ theta_1 ~-~
(n_1 ~\ sin\;\ theta_1) ~\ cos\;\ theta_2 ~\ sin\;\ theta_1} {
(n_1 ~\ sin\;\ theta_1) ~\ sin\;\ theta_2 ~\ cos\;\ theta_1 +~
(n_1 ~\ sin\;\ theta_1) ~\ cos\;\ theta_2 ~\ sin\;\ theta_1}
\ qquad\ text {(por la ley de Snell)}\\ [4pt]
&=~\ frac {\ sin\;\ theta_2 ~\ cos\;\ theta_1 ~-~
\ cos\;\ theta_2 ~\ sin\;\ theta_1} {
\ sin\;\ theta_2 ~\ cos\;\ theta_1 ~+~
\ cos\;\ theta_2 ~\ sin\;\ theta_1}\ [4pt]
&=~\ frac {\ sin\ ;(\ theta_2 -\ theta_1)} {\ sin\ ;(\ theta_2 +\ theta_1)}
\ fin {alinear*}\ nonumber\]

Los dos últimos ejemplos demuestran un aspecto importante de cómo se utilizan las identidades en la práctica: reconocer términos que forman parte de identidades conocidas, para que puedan ser factorizadas. Esta es una técnica común.