5.3: Funciones trigonométricas inversas
- Page ID
- 113478
Hemos mencionado brevemente las funciones trigonométricas inversas antes, por ejemplo en la Sección 1.3 cuando discutimos cómo usar los botones\(\fbox{\(\sin^{-1}\)}\),\(\fbox{\(\cos^{-1}\)}\), y\(\fbox{\(\tan^{-1}\)}\) en una calculadora para encontrar un ángulo que tenga cierto valor de función trigonométrica. Ahora definiremos esas funciones inversas y determinaremos sus gráficas.
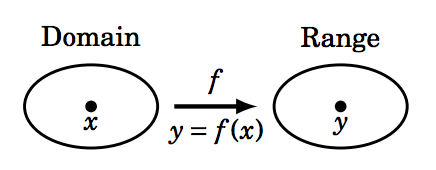
Recordemos que una función es una regla que asigna un solo objeto\(y \) de un conjunto (el rango a cada objeto\(x \) de otro conjunto (el dominio). Podemos escribir esa regla como\(y = f(x) \), donde\(f \) está la función (ver Figura 5.3.1). Existe una regla vertical simple para determinar si una regla\(y=f(x) \) es una función:\(f \) es una función si y solo si cada línea vertical interseca la gráfica de\(y=f(x) \) en el plano\(xy\) -coordenada como máximo una vez (ver Figura 5.3.2).
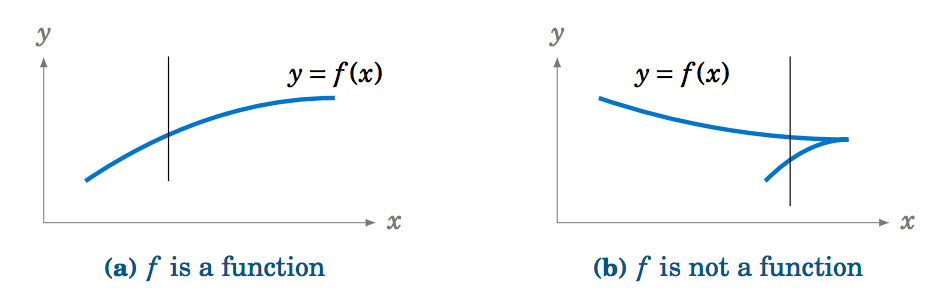
Recordemos que una función\(f \) es uno a uno (a menudo escrito como\(1-1\)) si asigna valores distintos de\(y \) a distintos valores de\(x \). En otras palabras, si\(x_1 \ne x_2 \) entonces\(f(x_1 ) \ne f(x_2 ) \). Equivalentemente,\(f \) es uno a uno si\(f(x_1 ) = f(x_2 ) \) implica\(x_1 = x_2 \). Existe una regla horizontal simple para determinar si una función\(y=f(x) \) es uno a uno:\(f \) es uno a uno si y solo si cada línea horizontal cruza la gráfica de\(y=f(x) \) en el plano\(xy\) de coordenadas como máximo una vez (ver Figura 5.3.3).
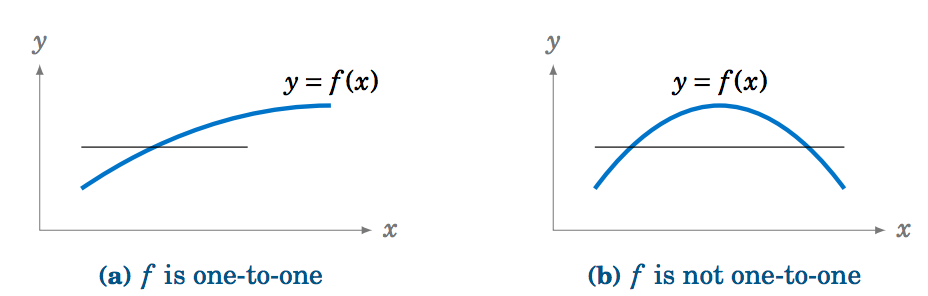
Si una función\(f \) es uno a uno en su dominio, entonces\(f \) tiene una función inversa, denotada por\(f^{-1} \), tal que\(y=f(x) \) si y solo si\(f^{-1}(y) = x \). El dominio de\(f^{-1} \) es el rango de\(f \).
La idea básica es que\(f^{-1} \) “deshace” lo que\(f \) hace, y viceversa. En otras palabras,
\ [\ nonumber\ begin {alignat*} {3}
f^ {-1} (f (x)) ~&=~ x\ quad&&\ text {para todos\(x \) en el dominio de\(f \), y}\\\ nonumber
f (f^ {-1} (y)) ~&=~ y\ quad&&\ text {para todos\(y \) en el rango de\(f \).}
\ end {alignat*}\ nonumber\]
Sabemos por sus gráficas que ninguna de las funciones trigonométricas es una a una en todos sus dominios. Sin embargo, podemos restringir esas funciones a subconjuntos de sus dominios donde son uno a uno. Por ejemplo,\(y=\sin\;x \) es uno a uno a lo largo del intervalo\(\left[ -\frac{\pi}{2},\frac{\pi}{2} \right] \), como vemos en la gráfica a continuación:
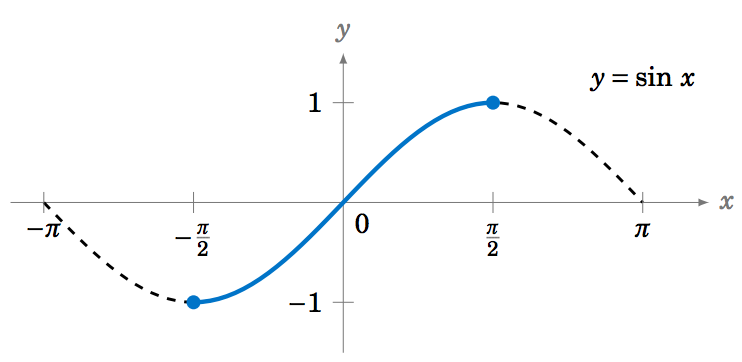
Porque\(-\frac{\pi}{2} \le x \le \frac{\pi}{2} \) tenemos\(-1 \le \sin\;x \le 1 \), así podemos definir la función sinusoidal inversa\(y=\sin^{-1} x \) (a veces llamada el arco seno y denotada por\(y=\arcsin\;x\)) cuyo dominio es el intervalo\([-1,1] \) y cuyo rango es el intervalo\(\left[ -\frac{\pi}{2},\frac{\pi}{2} \right] \). En otras palabras:
\ [\ begin {alignat} {3}
\ sin^ {-1} (\ sin\; y) ~&=~ y\ quad&&\ text {para\ (-\ tfrac {\ pi} {2}\ le y\ le
\ tfrac {\ pi} {2}\)}\ label {eqn:arcsin1}\\
\ sin\ ;(\ sin^ {-1} x) ~&=~ x\ quad&&\ text {for\(-1 \le x \le 1\)}\ label {eqn:arcsin2}
\ end {alignat}\ nonumber\]
Encuentra\(\sin^{-1} \left(\sin\;\frac{\pi}{4}\right) \).
Solución
Ya que\(-\frac{\pi}{2} \le \frac{\pi}{4} \le \frac{\pi}{2} \), sabemos que\(\sin^{-1} \left(\sin\;\frac{\pi}{4}\right) = \boxed{\frac{\pi}{4}}\; \), por Ecuación\ ref {eqn:arcsin1}.
Encuentra\(\sin^{-1} \left(\sin\;\frac{5\pi}{4}\right) \).
Solución
Ya que\(\frac{5\pi}{4} > \frac{\pi}{2} \), no podemos usar la ecuación\ ref {eqn:arcsin1}. Pero eso lo sabemos\(\sin\;\frac{5\pi}{4} = -\frac{1}{\sqrt{2}} \). Así,\(\sin^{-1} \left(\sin\;\frac{5\pi}{4}\right) = \sin^{-1} \left( -\frac{1}{\sqrt{2}} \right) \) es, por definición, el ángulo\(y \) tal que\(-\frac{\pi}{2} \le y \le \frac{\pi}{2} \) y\(\sin\;y = -\frac{1}{\sqrt{2}} \). Ese ángulo es\(y=-\frac{\pi}{4} \), ya que
\ [\ sin\;\ izquierda (-\ tfrac {\ pi} {4}\ derecha) ~=~ -\ sin\;\ izquierda (\ tfrac {\ pi} {4}\ derecha) ~=~
-\ tfrac {1} {\ sqrt {2}} ~. \ nonumber\]
Por lo tanto,\(\sin^{-1} \left(\sin\;\frac{5\pi}{4}\right) = \boxed{-\tfrac{\pi}{4}}\; \).
El ejemplo 5.14 ilustra un punto importante: siempre\(\sin^{-1} x \) debe ser un número entre\(-\frac{\pi}{2} \) y\(\frac{\pi}{2} \). Si obtienes un número fuera de ese rango, entonces cometiste un error en alguna parte. Es por esto que en el Ejemplo 1.27 en la Sección 1.5 obtuvimos\(\sin^{-1}(-0.682) = -43^\circ \) al usar el botón\(\fbox{\(\sin^{-1}\)}\) en una calculadora. En lugar de un ángulo entre\(0^\circ \) y\(360^\circ \) (es decir,\(0 \) a\(2\pi \) radianes) obtuvimos un ángulo entre\(-90^\circ \) y\(90^\circ \) (es decir,\(-\frac{\pi}{2} \) a\(\frac{\pi}{2} \) radianes).
En general, la gráfica de una función inversa\(f^{-1} \) es el reflejo de la gráfica de\(f \) alrededor de la línea\(y=x \). La gráfica de\(y=\sin^{-1} x \) se muestra en la Figura 5.3.5. Observe la simetría sobre la línea\(y=x \) con la gráfica de\(y=\sin\;x \).
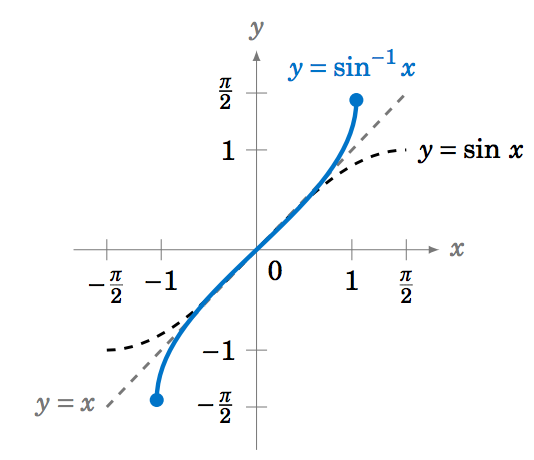
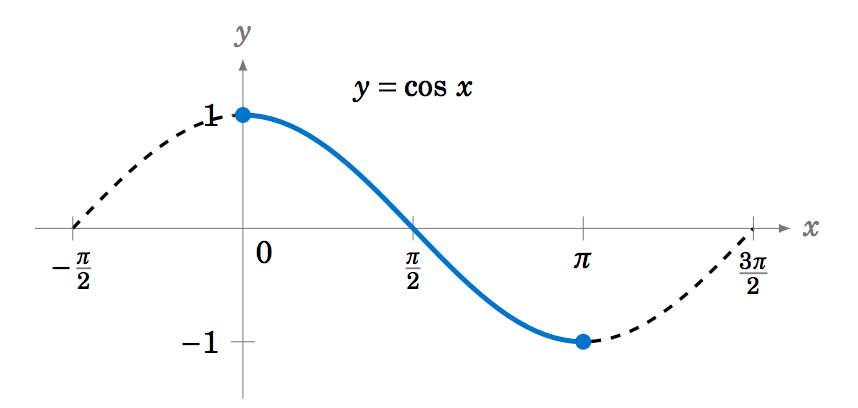
La función coseno inversa\(y=\cos^{-1} x \) (a veces llamada coseno arco y denotada por\(y=\arccos\;x\)) se puede determinar de manera similar. La función\(y=\cos\;x \) es uno a uno a lo largo del intervalo\([0,\pi] \), como vemos en la gráfica a continuación:
Así,\(y=\cos^{-1} x \) es una función cuyo dominio es el intervalo\([-1,1] \) y cuyo rango es el intervalo\([0,\pi] \). En otras palabras:
\ [\ begin {alignat} {3}
\ cos^ {-1} (\ cos\; y) ~&=~ y\ quad&&\ text {for\(0 \le y \le \pi\)}\ label {eqn:arccos1}\\
\ cos\ ;(\ cos^ {-1} x) ~&=~ x\ quad&&\ text {for\(-1 \le x \le 1\)}\ label {eqn:arccos2}
\ end {alignat}\ nonumber\]
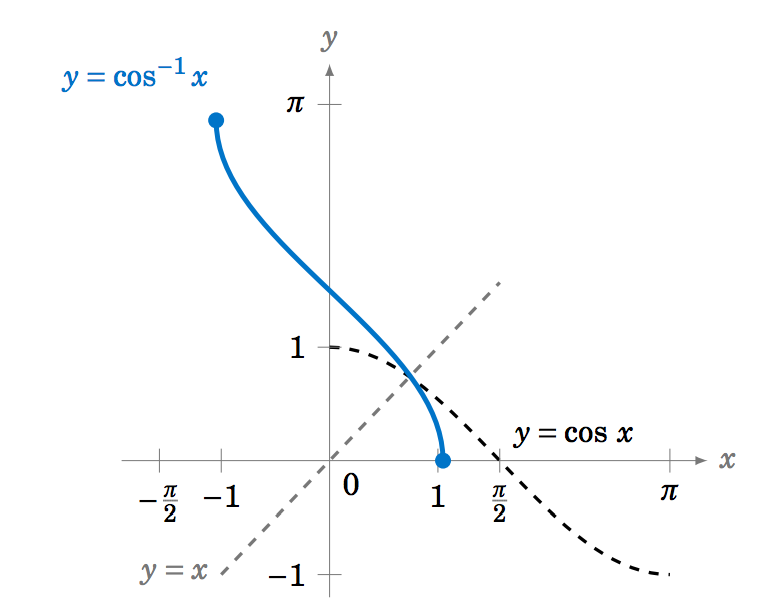
La gráfica de\(y=\cos^{-1} x \) se muestra a continuación en la Figura 5.3.7. Observe la simetría sobre la línea\(y=x \) con la gráfica de\(y=\cos\;x \).
Encuentra\(\cos^{-1} \left(\cos\;\frac{\pi}{3}\right) \).
Solución
Ya que\(0 \le \frac{\pi}{3} \le \pi \), sabemos que\(\cos^{-1} \left(\cos\;\frac{\pi}{3}\right) = \boxed{\frac{\pi}{3}}\; \), por Ecuación\ ref {eqn:arccos1}.
Encuentra\(\cos^{-1} \left(\cos\;\frac{4\pi}{3}\right) \).
Solución
Ya que\(\frac{4\pi}{3} > \pi \), no podemos usar la ecuación\ ref {eqn:arccos1}. Pero eso lo sabemos\(\cos\;\frac{4\pi}{3} = -\frac{1}{2} \). Así,\(\cos^{-1} \left(\cos\;\frac{4\pi}{3}\right) = \cos^{-1} \left( -\frac{1}{2} \right) \) es, por definición, el ángulo\(y \) tal que\(0 \le y \le \pi \) y\(\cos\;y = -\frac{1}{2} \). Ese ángulo es\(y=\frac{2\pi}{3} \) (i.e.\(120^\circ\)). Por lo tanto,\(\cos^{-1} \left(\cos\;\frac{4\pi}{3}\right) = \boxed{\tfrac{2\pi}{3}}\; \).
Los ejemplos 5.14 y 5.16 pueden resultar confusos, ya que parecen violar la regla general para funciones inversas que\(f^{-1}(f(x)) = x \) para todos\(x \) en el dominio de\(f \). Pero esa regla sólo se aplica cuando la función\(f \) es uno-a-uno sobre todo su dominio. Tuvimos que restringir las funciones seno y coseno a subconjuntos muy pequeños de sus dominios completos para que esas funciones fueran uno a uno. Esa regla general, por lo tanto, sólo se mantiene para\(x \) en esos subconjuntos pequeños en el caso del seno inverso y el coseno inverso.
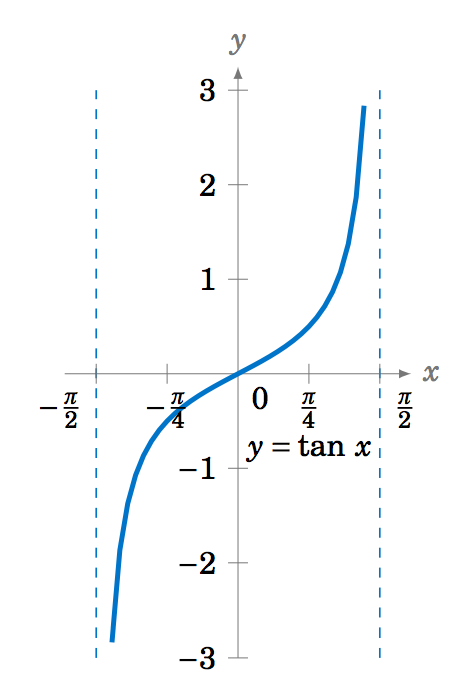
La función tangente inversa\(y=\tan^{-1} x \) (a veces llamada tangente de arco y denotada por\(y=\arctan\;x\)) se puede determinar de manera similar. La función\(y=\tan\;x \) es uno a uno a lo largo del intervalo\(\left( -\frac{\pi}{2},\frac{\pi}{2} \right) \), como vemos en la Figura 5.3.8:
La gráfica de\(y=\tan^{-1} x \) se muestra a continuación en la Figura 5.3.9. Observe que las asíntotas verticales para\(y=\tan\;x \) convertirse en asíntotas horizontales para\(y=\tan^{-1} x \). Tenga en cuenta también la simetría sobre la línea\(y=x \) con la gráfica de\(y=\tan\;x \).
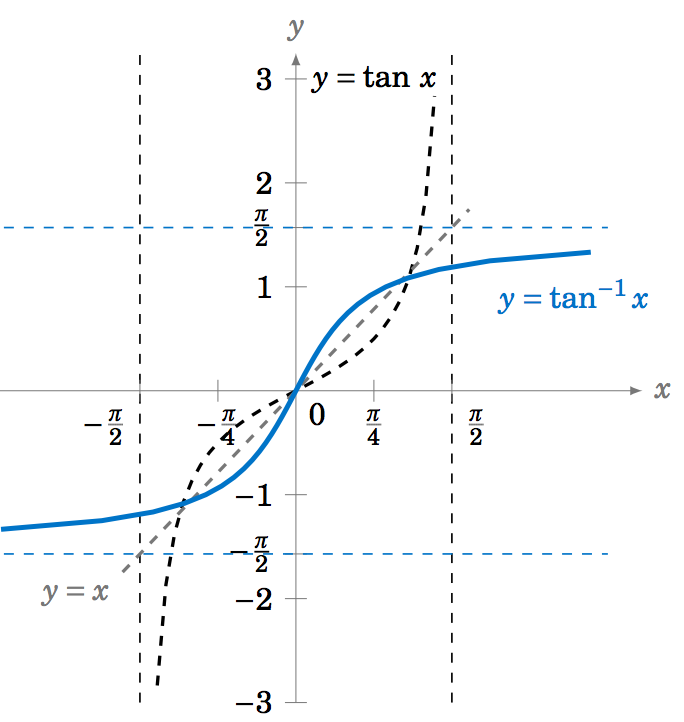
Así,\(y=\tan^{-1} x \) es una función cuyo dominio es el conjunto de todos los números reales y cuyo rango es el intervalo\(\left( -\frac{\pi}{2},\frac{\pi}{2} \right) \). En otras palabras:
\ [\ begin {alignat} {3}
\ tan^ {-1} (\ tan\; y) ~&=~ y\ quad&&\ text {for\ (-\ tfrac {\ pi} {2} < y <
\ tfrac {\ pi} {2}\)}\ label {eqn:arctan1}\\
\ tan\ ;(\ tan^ {-1} x) ~&=~ x\ quad&&\ text {para todos los reales\(x\)}\ label {eqn:arctan2}
\ end { alignat}\ nonumber\]
Encuentra\(\tan^{-1} \left(\tan\;\frac{\pi}{4}\right) \).
Solución
Ya que\(-\tfrac{\pi}{2} \le \tfrac{\pi}{4} \le \tfrac{\pi}{2} \), sabemos que\(\tan^{-1} \left(\tan\;\frac{\pi}{4}\right) = \boxed{\frac{\pi}{4}}\; \), por Ecuación\ ref {eqn:arctan1}.
Encuentra\(\tan^{-1} \left(\tan\;\pi\right) \).
Solución
Ya que\(\pi > \tfrac{\pi}{2} \), no podemos usar la ecuación\ ref {eqn:arctan1}. Pero eso lo sabemos\(\tan\;\pi = 0 \). Así,\(\tan^{-1} \left(\tan\;\pi\right) = \tan^{-1} 0 \) es, por definición, el ángulo\(y \) tal que\(-\tfrac{\pi}{2} \le y \le \tfrac{\pi}{2} \) y\(\tan\;y = 0 \). Ese ángulo es\(y=0 \). Por lo tanto,\(\tan^{-1} \left(\tan\;\pi \right) = \boxed{0}\; \).
Encuentra el valor exacto de\(\cos\;\left(\sin^{-1}\;\left(-\frac{1}{4}\right)\right) \).
Solución
Vamos\(\theta = \sin^{-1}\;\left(-\frac{1}{4}\right) \). Sabemos que\(-\tfrac{\pi}{2} \le \theta \le \tfrac{\pi}{2} \), así ya que\(\sin\;\theta = -\frac{1}{4} < 0 \),\(\theta \) debe estar en la QIV. De ahí\(\cos\;\theta > 0 \). Por lo tanto,
\ [\ cos^2\;\ theta ~=~ 1 ~-~\ sin^2\;\ theta ~=~ 1 ~-~\ izquierda (-\ frac {1} {4}\ derecha) ^2 ~=~\ frac {15} {16}
\ quad\ Rightarrow\ quad\ cos\;\ theta ~=~\ frac {\ sqrt {15}} 4} ~. \ nonumber\]
Tenga en cuenta que tomamos la raíz cuadrada positiva arriba desde entonces\(\cos\;\theta > 0 \). Por lo tanto,\(\cos\;\left(\sin^{-1}\;\left(-\frac{1}{4}\right)\right) = \boxed{\frac{\sqrt{15}}{4}}\; \).
\(\tan\;(\sin^{-1} x) = \dfrac{x}{\sqrt{1 - x^2}} \)Demuéstralo para\(-1 < x < 1 \).
Solución
Cuando\(x=0 \), la Ecuación se sostiene trivialmente, ya que
\[\nonumber \tan\;(\sin^{-1} 0) ~=~ \tan\;0 ~=~ 0 ~=~ \dfrac{0}{\sqrt{1 - 0^2}} ~. \nonumber \]
Ahora supongamos eso\(0 < x < 1 \). Vamos\(\theta = \sin^{-1} x \). Entonces\(\theta \) está en QI y\(\sin\;\theta = x \). Dibuja un triángulo rectángulo con un ángulo\(\theta \) tal que la pata opuesta tenga longitud\(x \) y la hipotenusa tenga longitud\(1 \), como en la Figura 5.3.10 (nótese que esto es posible desde entonces\(0 < x < 1\)). Entonces\(\sin\;\theta = \frac{x}{1} = x \). Por el Teorema de Pitágoras, la pierna adyacente tiene longitud\(\sqrt{1 - x^2} \). Por lo tanto,\(\tan\;\theta = \frac{x}{\sqrt{1 - x^2}} \).
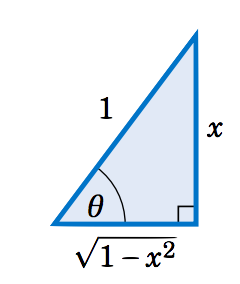
Si\(-1 < x < 0 \) entonces\(\theta = \sin^{-1} x \) está en QIV. Así podemos dibujar el mismo triángulo salvo que estaría “al revés” y volveríamos a tener\(\tan\;\theta = \frac{x}{\sqrt{1 - x^2}} \), ya que la tangente y el seno tienen el mismo signo (negativo) en QIV. Así,\(\tan\;(\sin^{-1} x) = \dfrac{x}{\sqrt{1 - x^2}} \) para\(-1 < x < 1 \).
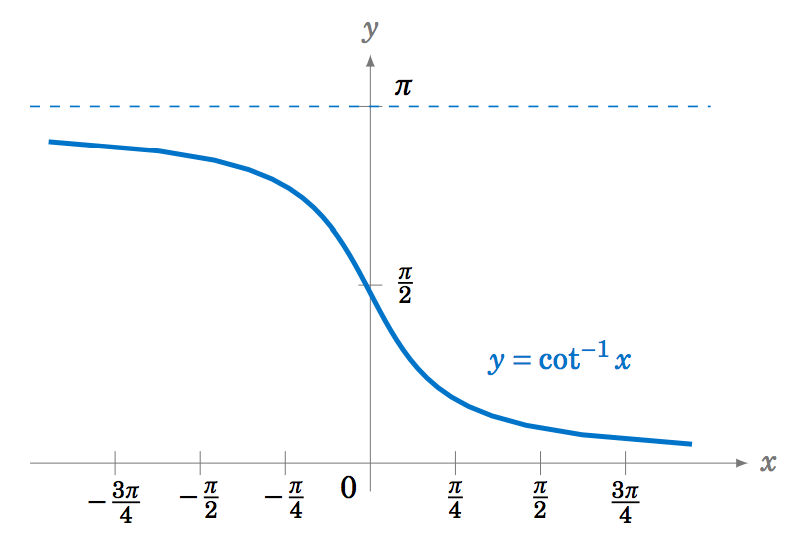
Las funciones inversas para cotangente, cosecante y secante se pueden determinar observando sus gráficas. Por ejemplo, la función\(y=\cot\;x \) es uno a uno en el intervalo\((0,\pi) \), donde tiene un rango igual al conjunto de todos los números reales. Así, la cotangente inversa\(y=\cot^{-1} x \) es una función cuyo dominio es el conjunto de todos los números reales y cuyo rango es el intervalo\((0,\pi) \). En otras palabras:
\ [\ begin {alignat} {3}
\ cot^ {-1} (\ cot\; y) ~&=~ y\ quad&&\ text {for\(0 < y < \pi\)}\ label {eqn:arccot1}\\
\ cot\ ;(\ cot^ {-1} x) ~&=~ x\ quad&&\ text {para todos los reales\(x\)}\ label {eqn:arccot2}
\ end {alignat}\ nonumber\]
La gráfica de\(y=\cot^{-1} x \) se muestra a continuación en la Figura 5.3.11.
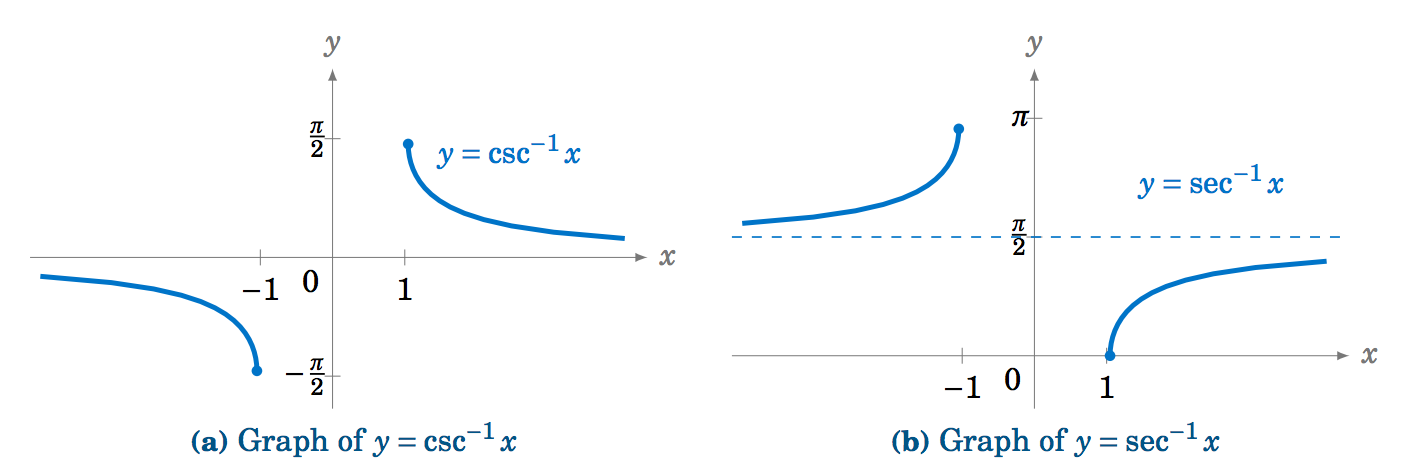
De igual manera, se puede demostrar que la cosecante inversa\(y=\csc^{-1} x \) es una función cuyo dominio es\(|x| \ge 1 \) y cuyo rango es\(-\frac{\pi}{2} \le y \le \frac{\pi}{2} \),\(y \ne 0 \). Asimismo, la secante inversa\(y=\sec^{-1} x \) es una función cuyo dominio es\(|x| \ge 1 \) y cuyo rango es\(0 \le y \le \pi \),\(y \ne \frac{\pi}{2} \).
\ [\ begin {alignat} {3}
\ csc^ {-1} (\ csc\; y) ~&=~ y\ quad&&\ text {for\ (-\ frac {\ pi} {2}\ le
y\ le\ frac {\ pi} {2}\),\(y \ne 0\)}\ label {eqn:arccsc1}\
\ csc\ ;(\ csc^ {-1} x) ~&=~ x\ quad&&\ text {for\(|x| \ge 1\)}\ label {eqn:arccsc2}
\ end { alignat}\ nonumber\]
\ [\ begin {alignat} {3}
\ sec^ {-1} (\ sec\; y) ~&=~ y\ quad&&\ text {for\(0 \le y \le \pi \),\ (y\ ne
\ frac {\ pi} {2}\)}\ label {eqn:arcsec1}\
\\ sec\ ;(\ sec^ {-1} x) ~&=~ x\ quad&&\ text para\(|x| \ge 1\)}\ label {eqn:arcsec2}
\ end {alignat}\ nonumber\]
También es común llamar\(\cot^{-1} x \),\(\csc^{-1} x \), y\(\sec^{-1} x \) el arco cotangente, arco cosecante, y arco secante, respectivamente, de\(x \). Las gráficas de\(y=\csc^{-1} x \) y\(y=\sec^{-1} x \) se muestran en la Figura 5.3.12:
Demostrar la identidad\(\tan^{-1} x \;+\; \cot^{-1} x ~=~ \frac{\pi}{2} \).
Solución:
Vamos\(\theta = \cot^{-1} x \). Usando las relaciones de la Sección 1.5, tenemos
\ [\ nonumber\ tan\;\ izquierda (\ tfrac {\ pi} {2} -\ theta\ derecha) ~=~ -\ tan\;\ izquierda (\ theta -\ tfrac {\ pi} {2}\ derecha)
~=~\ cuna\;\ theta ~=~\ cuna\ ;(\ cot^ {-1} x) ~=~ x ~,\ umber\]
por Ecuación\ ref {eqn:arccot2}. Entonces ya que\(\tan\;(\tan^{-1} x) = x \) para todos\(x \), esto significa eso\(\tan\;(\tan^{-1} x) = \tan\;\left( \tfrac{\pi}{2} - \theta \right) \). Por lo tanto,\(\tan\;(\tan^{-1} x) = \tan\;\left( \tfrac{\pi}{2} - \cot^{-1} x \right) \). Ahora, lo sabemos\(0 < \cot^{-1} x < \pi \), entonces, es decir\(-\tfrac{\pi}{2} < \tfrac{\pi}{2} - \cot^{-1} x < \tfrac{\pi}{2} \),\(\tfrac{\pi}{2} - \cot^{-1} x \) está en el subconjunto restringido en el que la función tangente es uno a uno. De ahí,\(\tan\;(\tan^{-1} x) = \tan\;\left( \tfrac{\pi}{2} - \cot^{-1} x \right)\) implica eso\(\tan^{-1} x = \tfrac{\pi}{2} - \cot^{-1} x \), lo que acredita la identidad.
¿Es\(\;\tan^{-1} a \;+\; \tan^{-1} b ~=~ \tan^{-1} \left( \dfrac{a+b}{1-ab} \right)\; \) una identidad?
Solución
En la Ecuación de suma tangente\(\tan\;(A+B) = \dfrac{\tan\;A \;+\; \tan\;B}{1 \;-\; \tan\;A~\tan\;B} \), let\(A = \tan^{-1} a \) y\(B = \tan^{-1} b \). Entonces
\ [\ nonumber\ begin {alinear*}
\ tan\ ;(\ tan^ {-1} a\; +\;\ tan^ {-1} b) ~&=~\ dfrac {\ tan\ ;(\ tan^ {-1} a)\; +\;\ tan\ ;(\ tan^ {-1}
b)} {1\; -\;\\ tan ;(\ tan^ {-1} b)} {1\; -\\ tan ;(\ tan^ {-1} a) ~\ tan\ ;(\ tan^ {-1} b)}\\\ nonumber
&=~\ dfrac {a+b} {1-ab}\ qquad\ text {por Ecuación\ ref {eqn:arctan2}, así parece que tenemos}\\\ nonumber
\ tan^ {-1} a\; +\;\ tan^ {-1} b ~&=~\ tan^ {-1}\ left (\ dfrac {a+b} {1-ab}\ derecha)
\ end {align*}\ nonumber\]
por definición de la tangente inversa. No obstante, recordemos eso\(-\tfrac{\pi}{2} < \tan^{-1} x < \tfrac{\pi}{2} \) para todos los números reales\(x \). Entonces, en particular, debemos tener\(-\tfrac{\pi}{2} < \tan^{-1} \left( \frac{a+b}{1-ab} \right) < \tfrac{\pi}{2} \). Pero es posible que no\(\tan^{-1} a \;+\; \tan^{-1} b \) esté en el intervalo\(\left(-\tfrac{\pi}{2},\tfrac{\pi}{2}\right) \). Por ejemplo,
\[ \tan^{-1} 1 \;+\; \tan^{-1} 2 ~=~ 1.892547 ~>~ \tfrac{\pi}{2} \approx 1.570796 ~.\nonumber \]
Y eso lo vemos\(\tan^{-1} \left( \frac{1+2}{1-(1)(2)} \right) = \tan^{-1} (-3) = -1.249045 \ne \tan^{-1} 1 \;+\; \tan^{-1} 2 \). Entonces la Ecuación sólo es cierta cuando\(-\tfrac{\pi}{2} < \tan^{-1} a \;+\; \tan^{-1} b < \tfrac{\pi}{2} \).


