5.E: Gráfica y Funciones Inversas (Ejercicios)

Última actualización
Guardar como PDF

Page ID: 113485

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Estos son ejercicios de tarea para acompañar el mapa de texto “Trigonometría Primaria” de Corral. Se trata de un texto sobre trigonometría elemental, diseñado para estudiantes que han cursado cursos de álgebra y geometría de secundaria. Aunque está diseñado para estudiantes universitarios, también podría usarse en escuelas secundarias. Se cubren los temas tradicionales, pero se toma un enfoque más geométrico de lo habitual. También se discuten algunos métodos numéricos (por ejemplo, el método secante para resolver ecuaciones trigonométricas).

5.1 Ejercicio

Para los Ejercicios 1-12, dibuje la gráfica de la función dada para$0 \le x \le 2\pi $.

5.1.1$y=-\cos\;x$

5.1.2$y=1+\sin\;x$

5.1.3$y=2-\cos\;x$

5.1.4$y=2-\sin\;x$

5.1.5 $y=-\tan\;x$

5.1.6$y=-\cot\;x$

5.1.7$y=1+\sec\;x$

5.1.8$y=-1-\csc\;x$

5.1.9$y=2\sin\;x$

5.1.10$y=-3\cos\;x$

5.1.11$y=-2\tan\;x$

5.1.12$y=-2\sec\;x$

5.1.13 Podemos extender la definición de círculo unitario del seno y el coseno funciones a las seis funciones trigonométricas. Dejar$P $ ser un punto en QI en el círculo unitario, de manera que el segmento de línea$\overline{OP} $ en la Figura 5.1.10 tenga longitud$1 $ y forme un ángulo agudo$\theta$ con el$x$ eje positivo. Identificar cada una de las seis funciones trigonométricas de$\theta $ con exactamente uno de los segmentos de línea en la Figura 5.1.10, teniendo en cuenta que el radio del círculo es$1 $. Para empezar, tenemos$\sin\;\theta = MP $ (¿por qué?).

$alt$
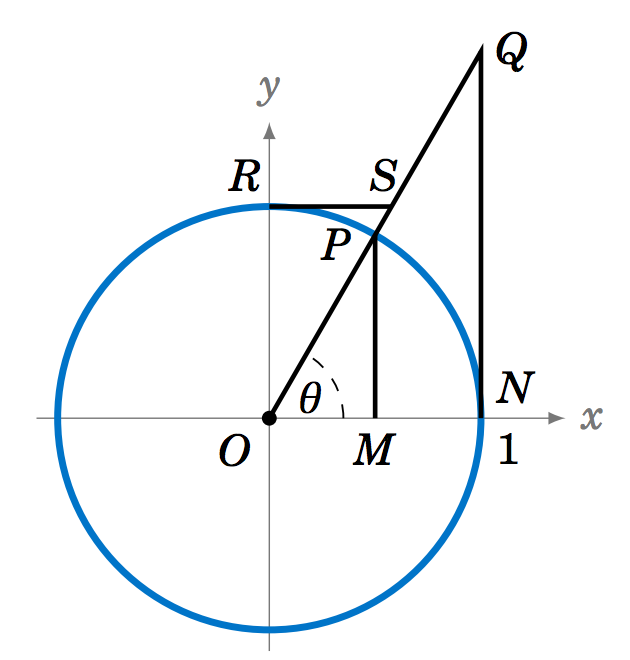
Figura 5.1.10

5.1.14 Para el Ejercicio 13, ¿cómo dibujarías los segmentos de línea en la Figura 5.1.10 si$\theta $ estuviera en la QII? Recordemos que algunas de las funciones trigonométricas son negativas en QII, por lo que tendrá que llegar a una convención sobre cómo tratar algunas de las longitudes de segmento de línea como negativas.

5.1.15 Para cualquier punto$(x,y) $ del círculo unitario y cualquier ángulo$\alpha $, mostrar que el punto$R_{\alpha} (x,y) $ definido por también$R_{\alpha} (x,y) = (x\,\cos\;\alpha \,-\, y\,\sin\;\alpha , x\,\sin\;\alpha \,+\, y\,\cos\;\alpha) $ está en el círculo unitario. ¿Cuál es la interpretación geométrica de$R_{\alpha} (x,y)$? Además,$R_{-\alpha} (R_{\alpha} (x,y)) = (x,y) $ demuéstralo y$R_{\beta} (R_{\alpha} (x,y)) = R_{\alpha + \beta} (x,y) $.

5.2 Ejercicio

Para los Ejercicios 1-12, encuentre la amplitud, el periodo y el desplazamiento de fase de la función dada. Después grafica un ciclo de la función, ya sea a mano o usando Gnuplot (ver Apéndice B).

5.2.1$y=3\,\cos\;\pi x$

5.2.2$y=\sin\;(2\pi x - \pi)$

5.2.3$y=-\sin\;(5x + 3)$

5.2.4$y=1+8\,\cos\;(6x- \pi)$

5.2.5 $y=2+\cos\;(5x + \pi)$

5.2.6$y=1-\sin\;(3\pi - 2x)$

5.2.7$y=1-\cos\;(3\pi - 2x)$

5.2.8$y=2\,\tan\;(x - 1)$

5.2.9$y=1-\tan\;(3\pi - 2x)$

5.2.10$y=\sec\;(2x + 1)$

5.2.11$y=2\csc\;(2x - 1)$

5.2.12$y=2+4\,\cot\;(1-x)$

5.2.13 Para la función$y=2\,\sin\;( x^2 ) $ del Ejemplo 5.8, para la cual los valores de $x$¿alcanza la función su valor máximo$2 $, y para qué valores de$x $ alcanza su valor mínimo$-2\,$?

5.2.14 Para la función$y=3\,\sin\;x + 4\,\cos\;x $ del Ejemplo 5.9,$x $ ¿para qué valores de la función alcanza su valor máximo$5 $, y para qué valores de$x $ alcanza su valor mínimo$-5\,$? Puedes restringir tus respuestas para que estén entre$0 $ y$2\pi $.

5.2.15 Grafica la función$y=\sin^2 \,x $ de$x=0 $ a$x=2\pi $, ya sea a mano o usando Gnuplot. ¿Cuáles son la amplitud y el periodo de esta función?

5.2.16 La corriente$i(t) $ en un circuito eléctrico de CA en el momento$t\ge 0 $ viene dada por$i(t) = I_m \,\sin\;\omega t $, y la tensión$v(t) $ viene dada por$v(t) = V_m \,\sin\;\omega t $, donde$V_m > I_m > 0 $ y$\omega > 0 $ son constantes. Dibuje un ciclo de ambos$i(t) $ y$v(t) $ juntos en la misma gráfica (es decir, en el mismo conjunto de ejes). ¿La corriente y el voltaje están en fase o fuera de fase?

5.2.17 Repita$i(t) $ el Ejercicio 16 con lo mismo que antes pero con$v(t)= V_m \,\sin\;\left(\omega t + \frac{\pi}{4}\right) $.

5.2.18 Repita el Ejercicio 16 con$i(t)=-I_m \,\cos\;\left(\omega t - \frac{\pi}{3}\right) $ y\ (v (t) =
V_m\,\ sin\;\ izquierda (\ omega t -\ frac {5\ pi} {6}\ derecha)\).

Para los Ejercicios 19-21, encuentra la amplitud y el periodo de la función dada. Después grafica un ciclo de la función, ya sea a mano o usando Gnuplot.

5.2.19$y=3\,\sin\;\pi x \;-\; 5\,\cos\;\pi x$

5.2.20$y=-5\,\sin\;3x \;+\; 12\,\cos\;3x$

5.2.21$y=2\,\cos\;x \;+\; 2\,\sin\;x$

5.2.22 Encuentra la amplitud de la función $y=2\,\sin\;( x^2 ) \;+\; \cos\;( x^2 ) $.

Para Ejercicios 23-25, encuentra el periodo de la función dada. Grafica un ciclo usando Gnuplot.

5.2.23$y=\sin\;3x \;-\; \cos\;5x$

5.2.24$y=\sin\;\frac{x}{3} \;+\; 2\,\cos\;\frac{3x}{4}$

5.2.25$y=2\,\sin\;\pi x \;+\; 3\,\cos\;\frac{\pi}{3}x$

5.2.26 Vamos$y = 0.5\,\sin\;x ~\sin\;12x\, $. Su gráfica para$x $ de$0 $ a$4\pi $ se muestra en la Figura 5.2.14:

$alt$
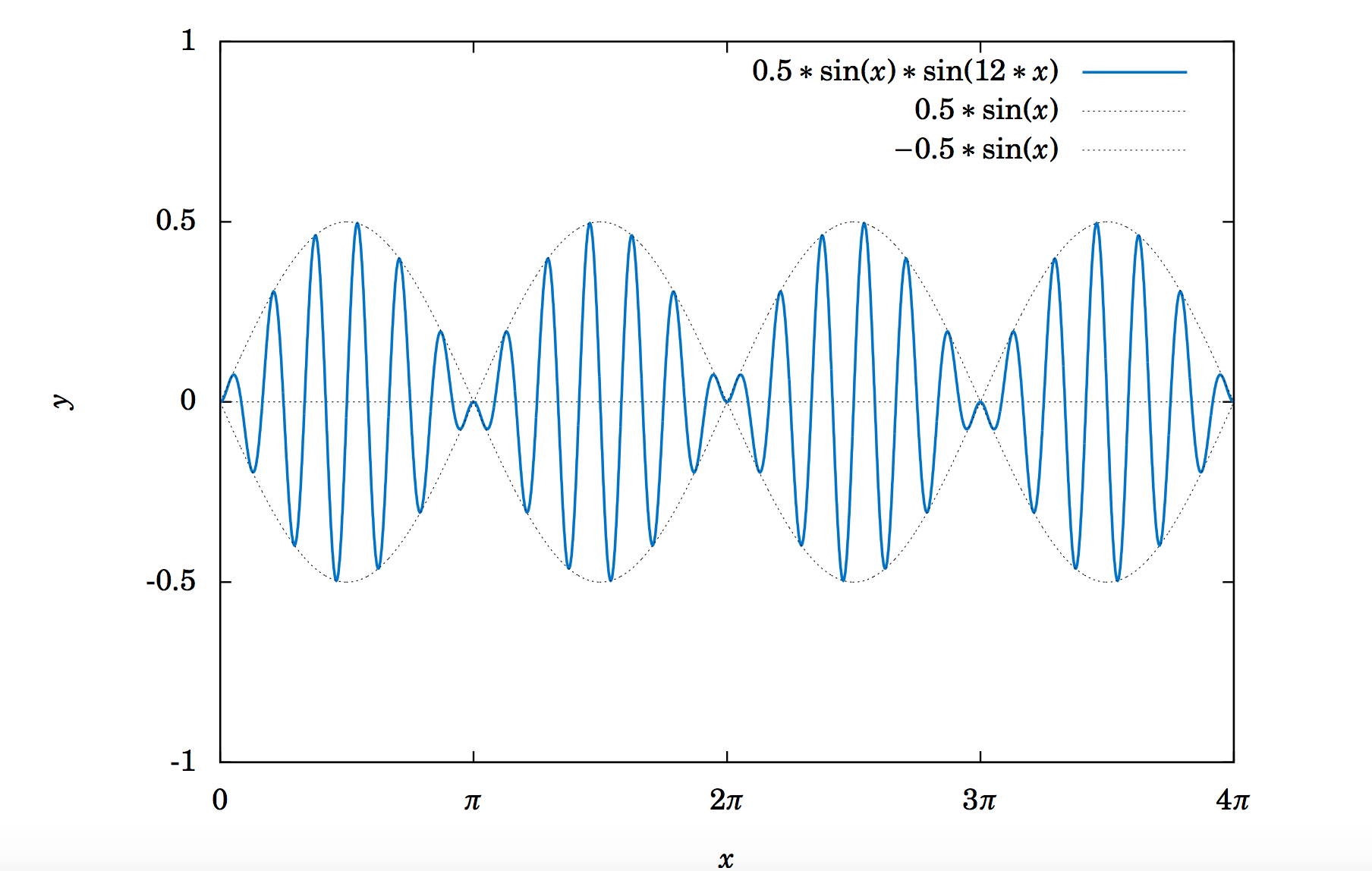
Figura 5.2.14 Onda modulada$y = 0.5 \sin x \sin 12x$

Se puede pensar en esta función como$\sin\;12x $ con una “amplitud” sinusoidalmente variable de$0.5\,\sin\;x $. ¿Cuál es el periodo de esta función? De la gráfica parece que la amplitud puede ser$0.5 $. Sin encontrar la amplitud exacta, explique por qué la amplitud es de hecho menor que$0.5 $. La función anterior se conoce como onda modulada, y las funciones$\pm\,0.5\,\sin\;x $ forman una envolvente de amplitud para la onda (es decir, encierran la onda). Utilice una identidad de la Sección 3.4 para escribir esta función como una suma de curvas sinusoidales.

5.2.27 Usa Gnuplot para graficar la función$y= x^2 \,\sin\;10x $ de$x = -2\pi $ a$x=2\pi $. ¿Qué funciones forman su envolvente de amplitud? (Nota: Uso$\texttt{set samples 500}$ en Gnuplot.)

5.2.28 Usa Gnuplot para graficar la función$y= \frac{1}{x^2} \,\sin\;80x $ de$x = 0.2 $ a$x=\pi $. ¿Qué funciones forman su envolvente de amplitud? (Nota: Uso$\texttt{set samples 500}$ en Gnuplot.)

5.2.29 ¿La función$y=\sin\;\pi x \;+\; \cos\;x $ tiene un periodo? Explique su respuesta.

5.2.30 Usa Gnuplot para graficar la función$y=\frac{\sin\;x}{x} $ de$x=-4\pi $ a$x=4\pi $. ¿Qué pasa en$x=0$?

5.3 Ejercicio

Para los Ejercicios 1-25, encuentra el valor exacto de la expresión dada en radianes.

5.3.1$\tan^{-1} 1$

5.3.2$\tan^{-1} \,(-1)$

5.3.3$\tan^{-1} 0$

5.3.4$\cos^{-1} 1$

5.3.5 $\cos^{-1} \,(-1)$

5.3.6$\cos^{-1} 0$

5.3.7$\sin^{-1} 1$

5.3.8$\sin^{-1} \,(-1)$

5.3.9$\sin^{-1} 0$

5.3.10$\sin^{-1} \left(\sin\;\frac{\pi}{3}\right)$

5.3.11$\sin^{-1} \left(\sin\;\frac{4\pi}{3}\right)$

5.3.12$\sin^{-1} \left(\sin\;\left(-\frac{5\pi}{6}\right)\right)$

5.3.13$\cos^{-1} \left(\cos\;\frac{\pi}{7}\right)$

5.3.14 $\cos^{-1} \left(\cos\;\left(-\frac{\pi}{10}\right)\right)$

5.3.15$\cos^{-1} \left(\cos\;\frac{6\pi}{5}\right)$

5.3.16$\tan^{-1} \left(\tan\;\frac{4\pi}{3}\right)$

5.3.17$\tan^{-1} \left(\tan\;\left(-\frac{5\pi}{6}\right)\right)$

5.3.18$\cot^{-1} \left(\cot\;\frac{4\pi}{3}\right)$

5.3.19$\csc^{-1} \left(\csc\;\left(-\frac{\pi}{9}\right)\right)$

5.3.20$\sec^{-1} \left(\sec\;\frac{6\pi}{5}\right)$

5.3.21$\cos\;\left(\sin^{-1}\;\left(\frac{5}{13}\right)\right)$

5.3.22$\cos\;\left(\sin^{-1}\;\left(-\frac{4}{5}\right)\right)$

5.3.23 $\sin^{-1}\;\frac{3}{5} \;+\; \sin^{-1}\;\frac{4}{5}$

5.3.24$\sin^{-1}\;\frac{5}{13} \;+\; \cos^{-1}\;\frac{5}{13}$

5.3.25$\tan^{-1}\;\frac{3}{5} \;+\; \cot^{-1}\;\frac{3}{5}$

Para los Ejercicios 26-33, acreditar la identidad dada.

5.3.26$\cos\;(\sin^{-1} x) ~=~ \sqrt{1 - x^2}$

5.3.27$\sin\;(\cos^{-1} x) ~=~ \sqrt{1 - x^2}$

5.3.28$\sin^{-1} x \;+\; \cos^{-1} x ~=~ \frac{\pi}{2}$

5.3.29$\sec^{-1} x \;+\; \csc^{-1} x ~=~ \frac{\pi}{2}$

5.3.30$\sin^{-1} (-x) ~=~ -\sin^{-1} x$

5.3.31$\cos^{-1} (-x) \;+\; \cos^{-1} x ~=~ \pi$

5.3.32$\cot^{-1} x ~=~ \tan^{-1} \,\frac{1}{x}~ $ para$x>0$

5.3.33$\tan^{-1} x \;+\; \tan^{-1} \,\frac{1}{x} ~=~ \frac{\pi}{2}~ $ para$x>0$

5.3.34 En el Ejemplo 5.22 demostramos que la fórmula$\;\tan^{-1} a \;+\; \tan^{-1} b ~=~ \tan^{-1} \left( \dfrac{a+b}{1-ab} \right)\; $ no siempre se sostiene. ¿Siempre se sostiene la fórmula$\tan\;(\tan^{-1} a \;+\; \tan^{-1} b ) ~=~ \dfrac{a+b}{1-ab} $, que formaba parte de ese ejemplo? Explique su respuesta.

5.3.35 Demuéstralo$\;\tan^{-1}\;\frac{1}{3}\;+\;\tan^{-1}\;\frac{1}{5} ~=~ \tan^{-1}\;\frac{4}{7}\; $.

5.3.36 Demuéstralo$\;\tan^{-1}\;\frac{1}{4}\;+\;\tan^{-1}\;\frac{2}{9} ~=~ \tan^{-1}\;\frac{1}{2}\; $.

5.3.37 La figura 5.3.13 muestra tres cuadrados iguales alineados uno contra el otro. Para los ángulos$\alpha $,$\beta $, y$\gamma $ en la imagen, muestran eso$\alpha = \beta + \gamma $. (Pista: Considera las tangentes de los ángulos. )

$alt$
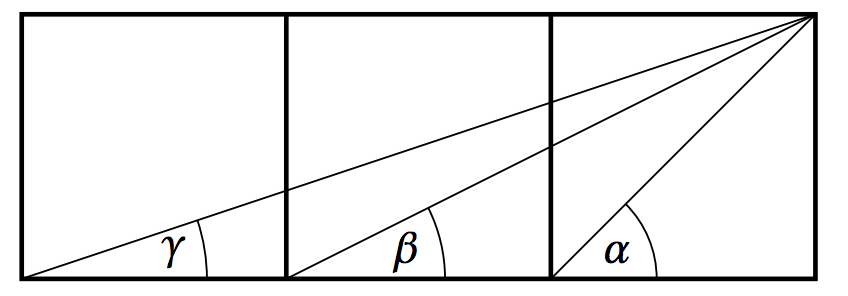
Figura 5.3.13 Ejercicio 37

5.3.38 Esbozar la gráfica de$y=\sin^{-1} 2x $.

5.3.39 Escribe un programa de computadora para resolver un triángulo en el caso en el que te den tres lados. Su programa debe leer en los tres lados como parámetros de entrada e imprimir los tres ángulos en grados como salida si existe una solución. Tenga en cuenta que dado que la mayoría de los lenguajes informáticos utilizan radianes para sus funciones trigonométricas inversas, es probable que tenga que hacer la conversión de radianes a grados usted mismo en el programa.