1.4: Composición de las funciones
- Page ID
- 121383
Objetivos de aprendizaje
- Combina funciones usando operaciones algebraicas.
- Crear una nueva función por composición de funciones.
- Evaluar funciones compuestas.
- Encuentra el dominio de una función compuesta.
- Descomponer una función compuesta en sus funciones componentes.
Supongamos que queremos calcular cuánto cuesta calentar una casa en un día determinado del año. El costo para calentar una casa dependerá de la temperatura media diaria, y a su vez, la temperatura media diaria depende del día particular del año. Observe cómo acabamos de definir dos relaciones: El costo depende de la temperatura, y la temperatura depende del día.
Usando variables descriptivas, podemos anotar estas dos funciones. La función\(C(T)\) da el costo\(C\) de calentar una casa para una temperatura diaria promedio dada en\(T\) grados centígrados. La función\(T(d)\) da la temperatura media diaria en el día d del año. Para cualquier día dado,\(Cost=C(T(d))\) significa que el costo depende de la temperatura, que a su vez depende del día del año. Así, podemos evaluar la función de costo a la temperatura\(T(d)\). Por ejemplo, podríamos evaluar\(T(5)\) para determinar la temperatura promedio diaria en el quinto día del año. Luego, podríamos evaluar la función de costo a esa temperatura. Nosotros escribiríamos\(C(T(5))\).
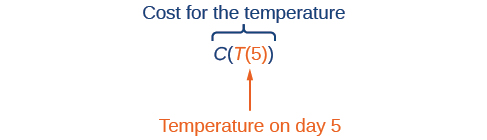
Al combinar estas dos relaciones en una sola función, hemos realizado la composición de funciones, que es el foco de esta sección.
Combinación de funciones mediante operaciones algebraicas
La composición de funciones es solo una forma de combinar funciones existentes. Otra forma es llevar a cabo las operaciones algebraicas habituales sobre funciones, como suma, resta, multiplicación y división. Esto lo hacemos realizando las operaciones con las salidas de la función, definiendo el resultado como la salida de nuestra nueva función.
Supongamos que necesitamos sumar dos columnas de números que representen los ingresos anuales separados de un esposo y una esposa a lo largo de un periodo de años, siendo el resultado el ingreso total del hogar. Queremos hacer esto por cada año, sumando solo los ingresos de ese año y luego recabando todos los datos en una nueva columna. Si\(w(y)\) es el ingreso de la esposa y\(h(y)\) es el ingreso del marido en el año\(y\), y\(T\) queremos representar el ingreso total, entonces podemos definir una nueva función.
\[T(y)=h(y)+w(y) \nonumber\]
Si esto es cierto para cada año, entonces podemos enfocarnos en la relación entre las funciones sin referencia a un año y escribir
\[T=h+w \nonumber\]
Al igual que para esta suma de dos funciones, podemos definir funciones de diferencia, producto y relación para cualquier par de funciones que tengan los mismos tipos de entradas (no necesariamente números) y también los mismos tipos de salidas (que tienen que ser números para que las operaciones habituales de álgebra puedan aplicarse a ellas, y cuáles también deben tener las mismas unidades o ninguna unidad cuando sumamos y restamos). De esta manera, podemos pensar en sumar, restar, multiplicar y dividir funciones.
Para dos funciones\(f(x)\) y\(g(x)\) con salidas de número real, definimos nuevas funciones\(f+g\)\(f−g\),\(fg\), y\(\frac{f}{g}\) por las relaciones.
\[ \begin{align*} (f+g)(x) &=f(x)+g(x) \\[4pt] (f−g)(x) &=f(x)−g(x) \\[4pt] (fg)(x)&=f(x)g(x) \\[4pt] \left(\dfrac{f}{g}\right)(x) &=\dfrac{f(x)}{g(x)} \end{align*}\]
Ejemplo\(\PageIndex{1}\): Performing Algebraic Operations on Functions
Encontrar y simplificar las funciones\((g−f)(x)\) y\(\left(\dfrac{g}{f}\right)(x)\), dado\(f(x)=x−1\) y\(g(x)=x^2−1\). ¿Son la misma función?
Solución
Comience por escribir la forma general, y luego sustituya las funciones dadas.
\[\begin{align*} (g−f)(x) &= g(x)−f(x) \\[4pt] (g−f)(x) &=x^2−1−(x−1) \\[4pt] &=x^2−x \\[4pt] &=x(x−1) \end{align*}\]
\[\begin{align*} \left(\dfrac{g}{f}\right)(x)&=g(x)f(x) \\[4pt] \left(\dfrac{g}{f}\right)(x)&=\dfrac{x^2−1}{x−1} \\[4pt] &=\dfrac{(x+1)(x−1)}{x−1} \\[4pt]&=x+1 \end{align*}\]
No, las funciones no son las mismas.
Nota: For\(\left(\dfrac{g}{f}\right)(x)\), la condición\(x\neq1\) es necesaria porque cuando\(x=1\), el denominador es igual a 0, lo que hace que la función sea indefinida.
Ejercicio\(\PageIndex{1}\)
Encuentre y simplifique las funciones\((fg)(x)\) y\((f−g)(x)\).
\[f(x)=x−1 \nonumber\]
y
\[g(x)=x^2−1 \nonumber\]
¿Son la misma función?
- Contestar
-
\((fg)(x)=f(x)g(x)=(x−1)(x2−1)=x^3−x^2−x+1 \\[4pt] (f−g)(x)=f(x)−g(x)=(x−1)−(x^2−1)=x−x^2\)
No, las funciones no son las mismas.
Crear una función por composición de funciones
Realizar operaciones algebraicas en funciones las combina en una nueva función, pero también podemos crear funciones componiendo funciones. Cuando queríamos calcular un costo de calefacción a partir de un día del año, creamos una nueva función que toma un día como entrada y produce un costo como salida. El proceso de combinar funciones para que la salida de una función se convierta en la entrada de otra se conoce como una composición de funciones. La función resultante se conoce como una función compuesta. Representamos esta combinación por la siguiente notación:
\[f{\circ}g(x)=f(g(x))\]
Leemos el lado izquierdo como “\(f\)compuesto con\(g\) at\(x\)” y el lado derecho como “\(f\)\(g\)de”\(x\). Los dos lados de la ecuación tienen el mismo significado matemático y son iguales. El símbolo de círculo abierto\(\circ\) se llama operador de composición. Utilizamos este operador principalmente cuando deseamos enfatizar la relación entre las funciones mismas sin hacer referencia a ningún valor de entrada particular. La composición es una operación binaria que toma dos funciones y forma una nueva función, tanto como suma o multiplicación toma dos números y da un nuevo número. Sin embargo, es importante no confundir la composición de funciones con la multiplicación porque, como aprendimos anteriormente, en la mayoría de los casos\(f(g(x)){\neq}f(x)g(x)\).
También es importante comprender el orden de las operaciones en la evaluación de una función compuesta. Seguimos la convención habitual con paréntesis comenzando primero por los paréntesis más internos, y luego trabajando hacia el exterior. En la ecuación anterior, la función\(g\) toma\(x\) primero la entrada y produce una salida\(g(x)\). Entonces la función\(f\) toma\(g(x)\) como entrada y produce una salida\(f(g(x))\).
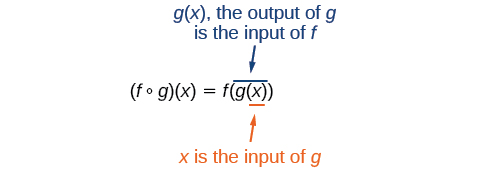
En general,\(f{\circ}g\) y\(g{\circ}f\) son diferentes funciones. Es decir, en muchos casos\(f(g(x)){\neq}g(f(x))\) para todos\(x\). También veremos que a veces se pueden componer dos funciones sólo en un orden específico.
Por ejemplo, si\(f(x)=x^2\) y\(g(x)=x+2\), entonces
\[\begin{align*} f(g(x))&= f(x+2) \\[4pt]&=(x+2)^2 \\[4pt] &=x^2+4x+4 \end{align*}\]
pero
\[\begin{align*} g(f(x))&= g(x^2) \\[4pt]&=x^2+2 \end{align*}\]
Estas expresiones no son iguales para todos los valores de x, por lo que las dos funciones no son iguales. Es irrelevante que las expresiones pasen a ser iguales para el único valor de entrada\(x=−\frac{1}{2}\).
Tenga en cuenta que el rango de la función interna (la primera función a evaluar) debe estar dentro del dominio de la función externa. De manera menos formal, la composición tiene que tener sentido en términos de entradas y salidas.
Composición de las funciones
Cuando la salida de una función se usa como entrada de otra, llamamos a toda la operación una composición de funciones. Para cualquier entrada\(x\) y funciones\(f\) y\(g\), esta acción define una función compuesta, que escribimos como\(f{\circ}g\) tal que
\[(f{\circ}g)(x)=f(g(x))\]
El dominio de la función compuesta\(f{\circ}g\) es todo\(x\) tal que\(x\) está en el dominio de\(g\) y\(g(x)\) está en el dominio de\(f\).
Es importante darse cuenta de que el producto de las funciones no\(fg\) es lo mismo que la composición de la función\(f(g(x))\), porque, en general,\(f(x)g(x){\neq}f(g(x))\).
Ejemplo\(\PageIndex{2}\): Determining whether Composition of Functions is Commutative
Usando las funciones proporcionadas, encontrar\(f(g(x))\) y\(g(f(x))\). Determinar si la composición de las funciones es conmutativa.
\[f(x)=2x+1 \;\;\;\; g(x)=3−x \nonumber\]
Solución
Empecemos por sustituir\(g(x)\) en\(f(x)\).
\[\begin{align*} f(g(x))&= 2(3−x)+1 \\[4pt] &=6−2x+1 \\[4pt] &=7−2x \end{align*}\]
Ahora podemos sustituir\(f(x)\) en\(g(x)\).
\[\begin{align*} g(f(x))&= 3−(2x+1) \\[4pt]&=3−2x−1 \\[4pt] &=2-2x \end{align*}\]
Encontramos eso\(g(f(x)){\neq}f(g(x))\), por lo que el funcionamiento de la composición de funciones no es conmutativa.
Ejemplo\(\PageIndex{3}\): Interpreting Composite Functions
La función\(c(s)\) da la cantidad de calorías quemadas completando\(s\) abdominales, y\(s(t)\) da la cantidad de abdominales que una persona puede completar en\(t\) minutos. Interpretar\(c(s(3))\).
Solución
La expresión interior en la composición es\(s(3)\). Porque la entrada a la\(s\) función -es tiempo,\(t=3\) representa 3 minutos, y\(s(3)\) es el número de abdominales completados en 3 minutos.
Usar\(s(3)\) como entrada a la función nos\(c(s)\) da el número de calorías quemadas durante el número de abdominales que se pueden completar en 3 minutos, o simplemente el número de calorías quemadas en 3 minutos (haciendo abdominales).
Ejemplo\(\PageIndex{4}\): Investigating the Order of Function Composition
Supongamos que\(f(x)\) da millas que se pueden conducir en\(x\) horas y\(g(y)\) da los galones de gas utilizados en la conducción de\(y\) millas. ¿Cuál de estas expresiones tiene sentido:\(f(g(y))\) o\(g(f(x))\)?
Solución
La función\(y=f(x)\) es una función cuya salida es el número de millas recorridas correspondiente al número de horas recorridas.
\[\text{number of miles } =f (\text{number of hours}) \nonumber\]
La función\(g(y)\) es una función cuya salida es el número de galones utilizados correspondiente al número de millas recorridas. Esto significa:
\[\text{number of gallons } =g(\text{number of miles}) \nonumber\]
La expresión\(g(y)\) toma millas como entrada y varios galones como salida. La función\(f(x)\) requiere un número de horas como entrada. Tratar de introducir varios galones no tiene sentido. La expresión\(f(g(y))\) carece de sentido.
La expresión\(f(x)\) toma horas como entrada y un número de millas conducidas como salida. La función\(g(y)\) requiere un número de millas como entrada. Usar\(f(x)\) (millas conducidas) como valor de entrada para\(g(y)\), donde galones de gas dependen de millas conducidas, tiene sentido. La expresión tiene\(g(f(x))\) sentido, y producirá el número de galones de gas utilizados,\(g\), conduciendo un cierto número de millas,\(f(x)\), en\(x\) horas.
Pregunta/Respuesta
¿Hay alguna situación en la\(g(f(x))\) que\(f(g(y))\) y ambas serían expresiones significativas o útiles?
Sí. Para muchas funciones matemáticas puras, ambas composiciones tienen sentido, aunque suelen producir nuevas funciones diferentes. En problemas del mundo real, las funciones cuyas entradas y salidas tienen las mismas unidades también pueden dar composiciones que son significativas en cualquier orden
Ejercicio\(\PageIndex{2}\)
La fuerza gravitacional sobre un planeta a una\(r\) distancia del sol viene dada por la función\(G(r)\). La aceleración de un planeta sometido a cualquier fuerza\(F\) viene dada por la función\(a(F)\). Formar una composición significativa de estas dos funciones, y explicar lo que significa.
- Contestar
-
Una fuerza gravitacional sigue siendo una fuerza, así\(a(G(r))\) que tiene sentido como la aceleración de un planeta a una\(r\) distancia del Sol (debido a la gravedad), pero\(G(a(F))\) no tiene sentido.
Evaluación de funciones compuestas
Una vez que componemos una nueva función a partir de dos funciones existentes, necesitamos poder evaluarla para cualquier entrada en su dominio. Esto lo haremos con entradas numéricas específicas para funciones expresadas como tablas, gráficas y fórmulas y con variables como entradas a funciones expresadas como fórmulas. En cada caso, evaluamos la función interna usando la entrada inicial y luego usamos la salida de la función interna como entrada para la función externa.
Evaluación de funciones compuestas mediante tablas
Al trabajar con funciones dadas como tablas, leemos los valores de entrada y salida de las entradas de la tabla y siempre trabajamos desde el interior hacia el exterior. Evaluamos primero la función inside y luego usamos la salida de la función inside como entrada a la función externa.
Ejemplo\(\PageIndex{5}\): Using a Table to Evaluate a Composite Function
Usando Tabla\(\PageIndex{1}\), evaluar\(f(g(3))\) y\(g(f(3))\).
| \(x\) | \(f(x)\) | \(g(x)\) |
|---|---|---|
| \ (x\)” style="vertical-align:middle; text-align:center;” class="lt-math-1296">1 | \ (f (x)\)” style="vertical-align:middle; text-align:center;” class="lt-math-1296">6 | \ (g (x)\)” style="vertical-align:middle; text-align:center;” class="lt-math-1296">3 |
| \ (x\)” style="vertical-align:middle; text-align:center;” class="lt-math-1296">2 | \ (f (x)\)” style="vertical-align:middle; text-align:center;” class="lt-math-1296">8 | \ (g (x)\)” style="vertical-align:middle; text-align:center;” class="lt-math-1296">5 |
| \ (x\)” style="vertical-align:middle; text-align:center;” class="lt-math-1296">3 | \ (f (x)\)” style="vertical-align:middle; text-align:center;” class="lt-math-1296">3 | \ (g (x)\)” style="vertical-align:middle; text-align:center;” class="lt-math-1296">2 |
| \ (x\)” style="vertical-align:middle; text-align:center;” class="lt-math-1296">4 | \ (f (x)\)” style="vertical-align:middle; text-align:center;” class="lt-math-1296">1 | \ (g (x)\)” style="vertical-align:middle; text-align:center;” class="lt-math-1296">7 |
Solución
Para evaluar\(f(g(3))\), partimos desde el interior con el valor de entrada 3. Luego evaluamos la expresión interior\(g(3)\) usando la tabla que define la función\(g: g(3)=2\). Entonces podemos usar ese resultado como la entrada a la función\(f\), por lo que\(g(3)\) se sustituye por 2 y obtenemos\(f(2)\). Entonces, usando la tabla que define la función\(f\), nos encontramos con eso\(f(2)=8\).
\[g(3)=2 \nonumber\]
\[f(g(3))=f(2)=8 \nonumber\]
Para evaluar\(g(f(3))\), primero evaluamos la expresión interna\(f(3)\) usando la primera tabla:\(f(3)=3\). Luego, usando la tabla para\(g\), podemos evaluar
\[g(f(3))=g(3)=2 \nonumber\]
Tabla\(\PageIndex{2}\) muestra las funciones compuestas\(f{\circ}g\) y\(g{\circ}f\) como tablas.
| \(x\) | \(g(x)\) | \(f(g(x))\) | \(f(x)\) | \(g(f(x))\) |
|---|---|---|---|---|
| \ (x\)” style="vertical-align:middle; text-align:center;” class="lt-math-1296">3 | \ (g (x)\)” style="vertical-align:middle; text-align:center;” class="lt-math-1296">2 | \ (f (g (x))\)” style="vertical-align:middle; text-align:center;” class="lt-math-1296">8 | \ (f (x)\)” style="vertical-align:middle; text-align:center;” class="lt-math-1296">3 | \ (g (f (x))\)” style="vertical-align:middle; text-align:center;” class="lt-math-1296">2 |
Ejercicio\(\PageIndex{3}\)
Usando Tabla\(\PageIndex{1}\), evaluar\(f(g(1))\) y\(g(f(4))\).
- Contestar
-
\(f(g(1))=f(3)=3\)y\(g(f(4))=g(1)=3\)
Evaluación de funciones compuestas mediante gráficos
Cuando se nos dan funciones individuales como gráficas, el procedimiento para evaluar funciones compuestas es similar al proceso que utilizamos para evaluar tablas. Leemos los valores de entrada y salida, pero esta vez, de los ejes x e y de las gráficas.
Cómo...
Dada una función compuesta y gráficas de sus funciones individuales, evaluarla utilizando la información proporcionada por las gráficas.
- Localice la entrada dada a la función interna en el eje x de su gráfica.
- Lee la salida de la función interna del eje y de su gráfica.
- Localice la salida de la función interna en el eje x de la gráfica de la función externa.
- Lea la salida de la función externa del eje y de su gráfica. Esta es la salida de la función compuesta.
Ejemplo\(\PageIndex{6}\): Using a Graph to Evaluate a Composite Function
Usando la Figura\(\PageIndex{3}\), evalúe\(f(g(1))\).
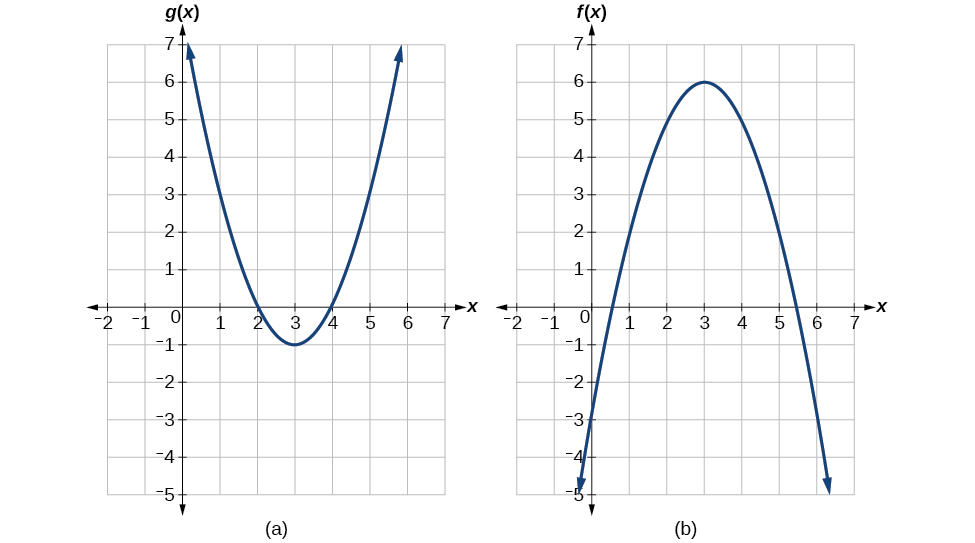
Solución
Para evaluar\(f(g(1))\), se inicia con la evaluación interna. Ver Figura\(\PageIndex{4}\).
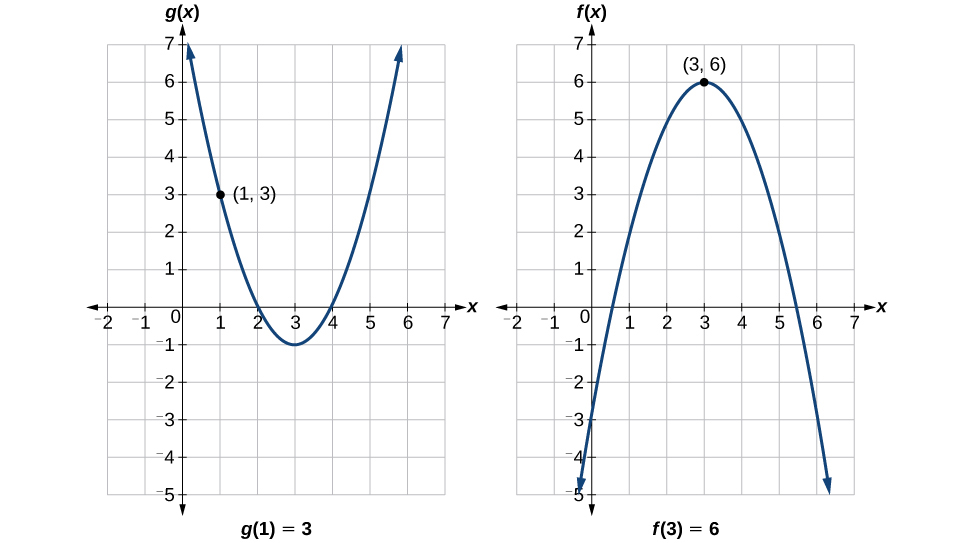
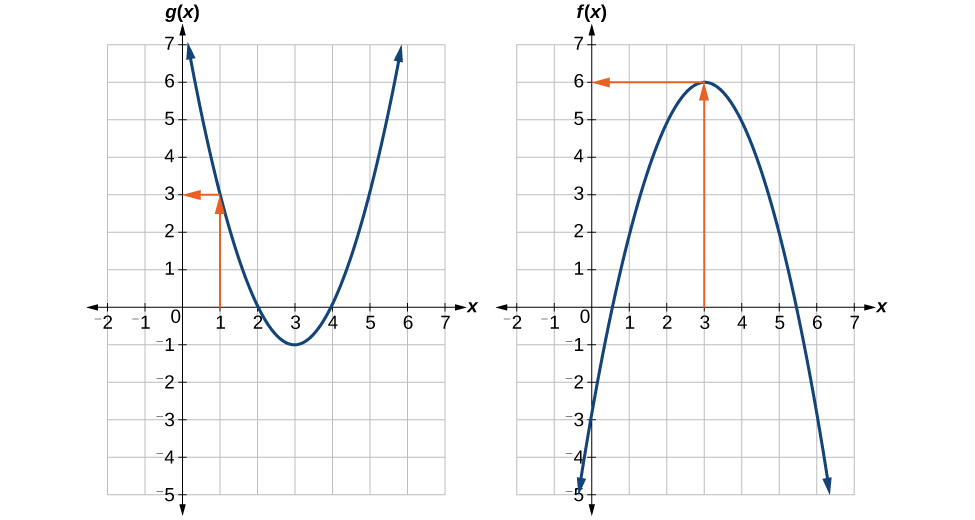
Evaluamos\(g(1)\) usando la gráfica de\(g(x)\), encontrando la entrada de 1 en el eje x y encontrando el valor de salida de la gráfica en esa entrada. Aquí,\(g(1)=3\). Utilizamos este valor como entrada a la función\(f\).
\[f(g(1))=f(3) \nonumber\]
Luego podemos evaluar la función compuesta mirando a la gráfica de\(f(x)\), encontrando la entrada de 3 en el eje x y leyendo el valor de salida de la gráfica en esta entrada. Aquí,\(f(3)=6\), entonces\(f(g(1))=6\).
Análisis
La figura\(\PageIndex{5}\) muestra cómo podemos marcar las gráficas con flechas para trazar la ruta desde el valor de entrada hasta el valor de salida.
Ejercicio\(\PageIndex{4}\)
Usando la Figura\(\PageIndex{3}\), evalúe\(g(f(2))\).
- Contestar
-
\(g(f(2))=g(5)=3\)
Evaluación de funciones compuestas mediante fórmulas
Al evaluar una función compuesta donde ya sea hemos creado o se nos han dado fórmulas, la regla de trabajar de adentro hacia afuera sigue siendo la misma. El valor de entrada a la función externa será la salida de la función interna, que puede ser un valor numérico, un nombre de variable o una expresión más complicada.
Si bien podemos componer las funciones para cada valor de entrada individual, a veces es útil encontrar una sola fórmula que calcule el resultado de una composición\(f(g(x))\). Para ello, ampliaremos nuestra idea de evaluación de funciones. Recordemos que, cuando evaluamos una función como\(f(t)=t^2−t\), sustituimos el valor dentro de los paréntesis en la fórmula donde veamos la variable de entrada.
Cómo...
Dada una fórmula para una función compuesta, evalúe la función.
- Evalúe la función interior utilizando el valor de entrada o la variable proporcionada.
- Utilice la salida resultante como entrada a la función externa.
Ejemplo\(\PageIndex{7}\): Evaluating a Composition of Functions Expressed as Formulas with a Numerical Input
Dado\(f(t)=t^2−t\) y\(h(x)=3x+2\), evaluar\(f(h(1))\).
Solución
Debido a que la expresión interior es\(h(1)\), comenzamos evaluando\(h(x)\) en 1.
\[ \begin{align*} h(1)=3(1)+2 \\[4pt] h(1)&=5 \end{align*} \]
Entonces\(f(h(1))=f(5)\), así evaluamos\(f(t)\) a una entrada de 5.
\[ \begin{align*} f(h(1)) &=f(5) \\[5pt] f(h(1))&=5^2−5 \\[5pt] f(h(1))&=20 \end{align*} \]
Análisis
No hace diferencia lo que las variables de entrada\(t\) y\(x\) fueron llamadas en este problema porque evaluamos para valores numéricos específicos.
Ejercicio\(\PageIndex{5}\)
Dado\(f(t)=t^2−t\) y\(h(x)=3x+2\), evaluar
a.\(h(f(2))\)
b.\(h(f(−2))\)
- Contestar a
-
8
- Respuesta b
-
20
Encontrar el dominio de una función compuesta
Como discutimos anteriormente, el dominio de una función compuesta como\(f{\circ}g\) es dependiente del dominio de\(g\) y del dominio de\(f\). Es importante saber cuándo podemos aplicar una función compuesta y cuándo no podemos, es decir, conocer el dominio de una función como\(f{\circ}g\). Supongamos que conocemos los dominios de las funciones\(f\) y\(g\) por separado. Si escribimos la función compuesta para una entrada\(x\) como\(f(g(x))\), podemos ver de inmediato que\(x\) debe ser miembro del dominio de g para que la expresión sea significativa, porque de lo contrario no podemos completar la evaluación de la función interna. No obstante, también vemos que\(g(x)\) debe ser miembro del dominio de\(f\), de lo contrario\(f(g(x))\) no se puede completar la evaluación de la segunda función en, y la expresión aún está indefinida. Así el dominio de\(f{\circ}g\) consiste únicamente en aquellas entradas en el dominio de\(g\) que producen salidas de\(g\) pertenecer al dominio de\(f\). Tenga en cuenta que el dominio de\(f\) compuesto con\(g\) es el conjunto de todos los\(x\) tales que\(x\) está en el dominio de\(g\) y g (x)\) está en el dominio de\(f\).
Definición: Dominio de una función compuesta
El dominio de una función compuesta\(f(g(x))\) es el conjunto de aquellas entradas\(x\) en el dominio de\(g\) para las cuales\(g(x)\) está en el dominio de\(f\).
Cómo...
Dada una composición de funciones\(f(g(x))\), determinar su dominio.
- Encuentra el dominio de\(g\).
- Encuentra el dominio de\(f\).
- Encuentra aquellas entradas\(x\) en el dominio de\(g\) para las cuales\(g(x)\) está en el dominio de\(f\). Es decir, excluir aquellas entradas\(x\) del dominio de\(g\) para las cuales no\(g(x)\) esté en el dominio de\(f\). El conjunto resultante es el dominio de\(f{\circ}g\).
Ejemplo\(\PageIndex{8A}\): Finding the Domain of a Composite Function
Encuentra el dominio de
\[(f∘g)(x) \text{ where } f(x)=\dfrac{5}{x−1} \text{ and } g(x)=\dfrac{4}{3x−2} \nonumber\]
Solución
El dominio de\(g(x)\) consiste en todos los números reales excepto\(x=\frac{2}{3}\), ya que ese valor de entrada provocaría que nos dividiéramos por 0. De igual manera, el dominio de\(f\) consiste en todos los números reales excepto 1. Por lo que necesitamos excluir del dominio de\(g(x)\) ese valor de\(x\) para el cual\(g(x)=1\).
\[\begin{align*} \dfrac{4}{3x-2}&= 1 \\[4pt] 4 &=3x-2 \\[4pt] 6&=3x \\[4pt] x&= 2 \end{align*}\]
Entonces el dominio de\(f{\circ}g\) es el conjunto de todos los números reales excepto\(\frac{2}{3}\) y\(2\). Esto significa que
\[x{\neq} \dfrac{2}{3} \text{ or } x\neq2 \nonumber\]
Podemos escribir esto en notación de intervalos como
\[\left(−\infty,\dfrac{2}{3}\right)\cup \left(\dfrac{2}{3},2 \right)\cup \left(2,\infty \right) \nonumber\]
Ejemplo\(\PageIndex{8B}\): Finding the Domain of a Composite Function Involving Radicals
Encuentra el dominio de
\[(f{\circ}g)(x) \text{ where } f(x)=\sqrt{x+2} \text{ and } g(x)=\sqrt{3−x} \nonumber\]
Solución
Porque no podemos tomar la raíz cuadrada de un número negativo, el dominio de\(g\) es\(\left(−\infty,3\right]\). Ahora comprobamos el dominio de la función compuesta
\[(f{\circ}g)(x)=\sqrt{\sqrt{3−x}+2} \nonumber\]
Porque\((f∘g)(x)=\sqrt{ \sqrt{3−x}+2},\sqrt{3−x}+2≥0,\) ya que el radicando de una raíz cuadrada debe ser positivo. Dado que las raíces cuadradas son positivas\(\sqrt{3−x}≥0\),, o,\(3−x≥0,\) lo que da un dominio de\((-∞,3]\).
Análisis
Este ejemplo muestra que el conocimiento del rango de funciones (específicamente la función interna) también puede ser útil para encontrar el dominio de una función compuesta. También muestra que el dominio de\(f{\circ}g\) puede contener valores que no están en el dominio de\(f\), aunque deben estar en el dominio de\(g\).
Ejercicio\(\PageIndex{6}\)
Encuentra el dominio de
\[(f{\circ}g)(x) \text{ where } f(x)=\dfrac{1}{x−2} \text{ and } g(x)=\sqrt{x+4} \nonumber\]
- Contestar
-
\([−4,0)∪(0,∞)\)
Descomponer una función compuesta en sus funciones componentes
En algunos casos, es necesario descomponer una función complicada. En otras palabras, podemos escribirlo como una composición de dos funciones más simples. Puede haber más de una manera de descomponer una función compuesta, por lo que podemos elegir la descomposición que parezca más conveniente.
Ejemplo\(\PageIndex{9}\): Decomposing a Function
Escribir\(f(x)=\sqrt{5−x^2}\) como la composición de dos funciones.
Solución
Estamos buscando dos funciones,\(g\) y\(h\), entonces\(f(x)=g(h(x))\). Para ello, buscamos una función dentro de una función en la fórmula para\(f(x)\). Como una posibilidad, podríamos notar que la expresión\(5−x^2\) es el interior de la raíz cuadrada. Entonces podríamos descomponer la función como
\[h(x)=5−x^2 \text{ and } g(x)=\sqrt{x} \nonumber\]
Podemos verificar nuestra respuesta recomponiendo las funciones.
\[g(h(x))=g(5−x^2)=\sqrt{5−x^2} \nonumber\]
Ejercicio\(\PageIndex{7}\)
Escribir\(f(x)=\dfrac{4}{3−\sqrt{4+x^2}}\) como la composición de dos funciones.
- Contestar
-
Posibles respuestas:
\(g(x)=\sqrt{4+x^2}\)
\(h(x)=\dfrac{4}{3−x}\)
\(f=h{\circ}g\)
Acceda a estos recursos en línea para obtener instrucción adicional y práctica con funciones compuestas.
- Funciones compuestas (http://openstaxcollege.org/l/compfunction)
- Aplicación de notación de funciones compuestas (http://openstaxcollege.org/l/compfuncnot)
- Funciones compuestas mediante gráficos (http://openstaxcollege.org/l/compfuncgraph)
- Funciones de descomponer (http://openstaxcollege.org/l/decompfunction)
- Valores de funciones compuestas (http://openstaxcollege.org/l/compfuncvalue)
Ecuación Clave
- Función compuesta\((f{\circ}g)(x)=f(g(x))\)
Conceptos clave
- Podemos realizar operaciones algebraicas en funciones. Ver Ejemplo.
- Cuando se combinan funciones, la salida de la primera función (interna) se convierte en la entrada de la segunda función (externa).
- La función producida al combinar dos funciones es una función compuesta. Ver Ejemplo y Ejemplo.
- Se debe considerar el orden de composición de funciones al interpretar el significado de las funciones compuestas. Ver Ejemplo.
- Una función compuesta se puede evaluar evaluando la función interna usando el valor de entrada dado y luego evaluando la función externa tomando como entrada la salida de la función interna.
- Una función compuesta se puede evaluar a partir de una tabla. Ver Ejemplo.
- Una función compuesta se puede evaluar a partir de una gráfica. Ver Ejemplo.
- Una función compuesta se puede evaluar a partir de una fórmula. Ver Ejemplo.
- El dominio de una función compuesta consiste en aquellas entradas en el dominio de la función interna que corresponden a salidas de la función interna que están en el dominio de la función externa. Ver Ejemplo y Ejemplo.
- Así como las funciones se pueden combinar para formar una función compuesta, las funciones compuestas se pueden descomponer en funciones más simples.
- Las funciones a menudo se pueden descomponer de más de una manera. Ver Ejemplo.
Glosario
- función compuesta
-
la nueva función formada por la composición de funciones, cuando la salida de una función se utiliza como entrada de otra