2.2: Gráficas de Funciones Lineales

Objetivos de aprendizaje

• Gráfica funciones lineales.
• Escribe la ecuación para una función lineal a partir de la gráfica de una línea.
• Dadas las ecuaciones de dos líneas, determinar si sus gráficas son paralelas o perpendiculares.
• Escribe la ecuación de una línea paralela o perpendicular a una línea dada.
• Resolver un sistema de ecuaciones lineales.

Dos compañías telefónicas competidoras ofrecen diferentes planes de pago. Los dos planes cobran la misma tarifa por minuto de larga distancia, pero cobran una tarifa plana mensual diferente. Un consumidor quiere determinar si los dos planes alguna vez costarán la misma cantidad por un número dado de minutos de larga distancia utilizados. El costo total de cada plan de pago puede ser representado por una función lineal. Para resolver el problema, necesitaremos comparar las funciones. En esta sección, consideraremos métodos de comparación de funciones usando gráficas.

Graficar funciones lineales

Anteriormente, vimos que la gráfica de una función lineal es una línea recta. También pudimos ver los puntos de la función así como el valor inicial a partir de una gráfica. Al graficar dos funciones, entonces, podemos comparar más fácilmente sus características. Existen tres métodos básicos para graficar funciones lineales:

1. Trazar los puntos y luego dibujar una línea a través de los puntos.
2. Utilice la intercepción y y la pendiente.
3. Utilizar transformaciones de la función de identidad\(f(x)=x\).

Graficar una función trazando puntos

Para encontrar puntos de una función, podemos elegir valores de entrada, evaluar la función en estos valores de entrada y calcular valores de salida. Los valores de entrada y los correspondientes valores de salida forman pares de coordenadas. Luego trazamos los pares de coordenadas en una cuadrícula. En general, debemos evaluar la función en un mínimo de dos entradas para encontrar al menos dos puntos en la gráfica. Por ejemplo, dada la función,\(f(x)=2x\), podríamos usar los valores de entrada 1 y 2. Al evaluar la función para un valor de entrada de 1 se obtiene un valor de salida de 2, que se representa por el punto\((1,2)\). Al evaluar la función para un valor de entrada de 2 se obtiene un valor de salida de 4, que está representado por el punto\((2,4)\). Elegir tres puntos suele ser aconsejable porque si los tres puntos no caen en la misma línea, sabemos que cometemos un error.

Cómo: Dada una función lineal, graficar trazando puntos.

1. Elija un mínimo de dos valores de entrada.
2. Evaluar la función en cada valor de entrada.
3. Utilice los valores de salida resultantes para identificar pares de coordenadas.
4. Trazar los pares de coordenadas en una cuadrícula.
5. Dibuja una línea a través de los puntos.

Ejemplo\(\PageIndex{1}\): Graphing by Plotting Points

\(f(x)=−\frac{2}{3}x+5\)Gráfica trazando puntos.

Solución

Comience por elegir los valores de entrada. Esta función incluye una fracción con un denominador de 3, así que vamos a elegir múltiplos de 3 como valores de entrada. Nosotros elegiremos 0, 3 y 6.

Evalúe la función en cada valor de entrada y use el valor de salida para identificar pares de coordenadas.

\[\begin{align*} x&=0 & f(0)&=-\dfrac{2}{3}(0)+5=5\rightarrow(0,5) \\ x&=3 & f(3)&=-\dfrac{2}{3}(3)+5=3\rightarrow(3,3) \\ x&=6 & f(6)&=-\dfrac{2}{3}(6)+5=1\rightarrow(6,1) \end{align*}\]

Traza los pares de coordenadas y dibuja una línea a través de los puntos. La figura\(\PageIndex{1}\) representa la gráfica de la función\(f(x)=−\frac{2}{3}x+5\).

Figura\(\PageIndex{1}\): La gráfica de la función lineal\(f(x)=−\frac{2}{3}x+5\).

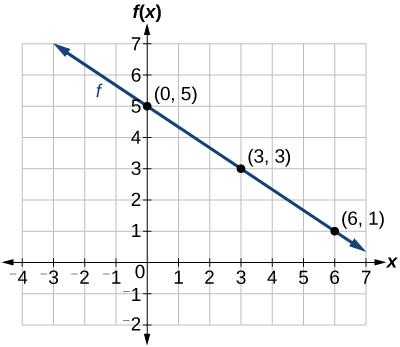
Análisis

El gráfico de la función es una línea como se esperaba para una función lineal. Además, la gráfica tiene una inclinación hacia abajo, lo que indica una pendiente negativa. Esto también se espera de la tasa constante negativa de cambio en la ecuación para la función.

Ejercicio\(\PageIndex{1}\)

\(f(x)=−\frac{3}{4}x+6\)Gráfica trazando puntos.

Contestar

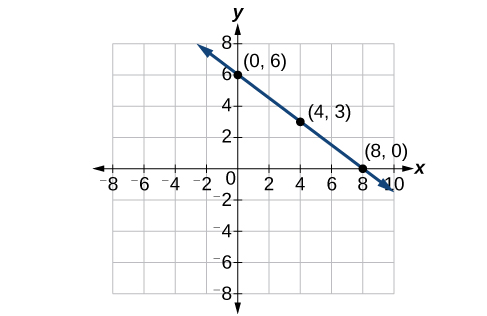
Figura\(\PageIndex{2}\)

Graficar una Función Usando Intercept Y y Talud

Otra forma de graficar funciones lineales es mediante el uso de características específicas de la función en lugar de trazar puntos. La primera característica es su intersección y, que es el punto en el que el valor de entrada es cero. Para encontrar la intersección y, podemos establecer\(x=0\) en la ecuación.

La otra característica de la función lineal es su pendiente\(m\), que es una medida de su inclinación. Recordemos que la pendiente es la tasa de cambio de la función. La pendiente de una función es igual a la relación entre el cambio en las salidas y el cambio en las entradas. Otra forma de pensar sobre la pendiente es dividiendo la diferencia vertical, o subida, por la diferencia horizontal, o correr. Encontramos tanto la intersección y como la pendiente en Funciones Lineales.

Consideremos la siguiente función.

\[f(x)=\dfrac{1}{2}x+1\]

El desnivel es\(\frac{1}{2}\). Debido a que la pendiente es positiva, sabemos que la gráfica se inclinará hacia arriba de izquierda a derecha. La intersección y es el punto en la gráfica cuando\(x=0\). La gráfica cruza el eje y en\((0,1)\). Ahora conocemos la pendiente y la intercepción en y. Podemos comenzar a graficar trazando el punto\((0,1)\) Sabemos que la pendiente es subida sobre corrida,\(m=\frac{\text{rise}}{\text{run}}\). De nuestro ejemplo, tenemos\(m=\frac{1}{2}\), lo que significa que la subida es 1 y la corrida es 2. Entonces, a partir de nuestra intersección y\((0,1)\), podemos subir 1 y luego correr 2, o correr 2 y luego subir 1. Repetimos hasta que tengamos algunos puntos, y luego dibujamos una línea a través de los puntos como se muestra en la Figura\(\PageIndex{3}\).

Figura\(\PageIndex{3}\): Gráfica de\(f(x)\) muestra pendiente e intersección en y

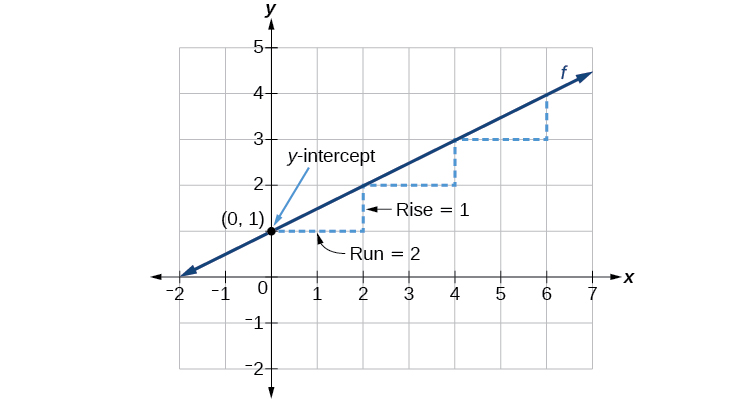
Interpretación gráfica de una función lineal

En la ecuación\(f(x)=mx+b\)

• \(b\)es la intersección y de la gráfica e indica el punto\((0,b)\) en el que la gráfica cruza el eje y.
• \(m\)es la pendiente de la línea e indica el desplazamiento vertical (subida) y el desplazamiento horizontal (recorrido) entre cada par de puntos sucesivos. Recordemos la fórmula para la pendiente:

\[m=\dfrac{\text{change in output (rise)}}{\text{change in input (run)}}=\dfrac{{\Delta}y}{{\Delta}x}=\dfrac{y_2-y_1}{x_2-x_1}\]

Ejercicio\(\PageIndex{1}\)

¿Todas las funciones lineales tienen intercepciones y?

Contestar

Sí. Todas las funciones lineales cruzan el eje y y, por lo tanto, tienen intercepciones y. (Nota: Una línea vertical paralela al eje y no tiene una intersección y, pero no es una función).

Cómo: Dada la ecuación para una función lineal, graficar la función usando la intersección y y la pendiente.

1. Evalúe la función en un valor de entrada de cero para encontrar la intersección y.
2. Identificar la pendiente como la tasa de cambio del valor de entrada.
3. Trazar el punto representado por la intercepción y.
4. Se usa\(\frac{\text{rise}}{\text{run}}\) para determinar al menos dos puntos más en la línea.
5. Esboza la línea que pasa por los puntos.

Ejemplo\(\PageIndex{2}\): Graphing by Using the y-intercept and Slope

Gráfica\(f(x)=−\frac{2}{3}x+5\) usando la intersección y y la pendiente.

Solución

Evaluar la función en\(x=0\) para encontrar la intersección y. El valor de salida cuando\(x=0\) es 5, por lo que la gráfica cruzará el eje y en\((0,5)\).

Según la ecuación para la función, la pendiente de la línea es\(-\frac{2}{3}\). Esto nos dice que por cada disminución vertical en la “subida” de —2 unidades, la “carrera” aumenta en 3 unidades en la dirección horizontal. Ahora podemos graficar la función trazando primero la intersección y en la gráfica de la Figura\(\PageIndex{4}\). Desde el valor inicial\((0,5)\) bajamos 2 unidades y hacia la derecha 3 unidades. Podemos extender la línea hacia la izquierda y hacia la derecha repitiendo, y luego dibujar una línea a través de los puntos.

Figura\(\PageIndex{4}\): Gráfica de\(f(x)\)

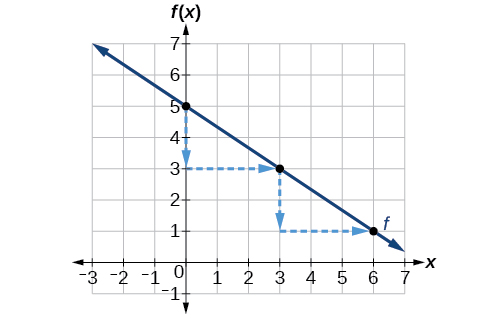
Análisis

La gráfica se inclina hacia abajo de izquierda a derecha, lo que significa que tiene una pendiente negativa como se esperaba.

Ejercicio\(\PageIndex{2}\)

Encuentra un punto en la gráfica que dibujamos en Ejemplo\(\PageIndex{2}\) que tiene un valor x negativo.

Contestar

Las posibles respuestas incluyen\((−3,7)\),\((−6,9)\), o\((−9,11)\).

Graficar una función mediante transformaciones

Otra opción para graficar es utilizar transformaciones de la función de identidad\(f(x)=x\). Una función puede ser transformada por un cambio hacia arriba, abajo, izquierda o derecha. Una función también se puede transformar usando una reflexión, estiramiento o compresión.

Estiramiento vertical o compresión

En la ecuación\(f(x)=mx\), el\(m\) está actuando como el estiramiento vertical o compresión de la función de identidad. Cuando\(m\) es negativo, también hay una reflexión vertical de la gráfica. Observe en Figura\(\PageIndex{5}\) que multiplicar la ecuación de\(f(x)=x\) por\(m\) estira la gráfica de\(f\) por un factor de\(m\) unidades si\(m>1\) y comprime la gráfica de\(f\) por un factor de\(m\) unidades si\(0<m<1\). Esto significa que cuanto mayor sea el valor absoluto de\(m\), más pronunciada será la pendiente.

Figura\(\PageIndex{5}\): Estiramientos verticales y compresiones y reflexiones sobre la función\(f(x)=x\).

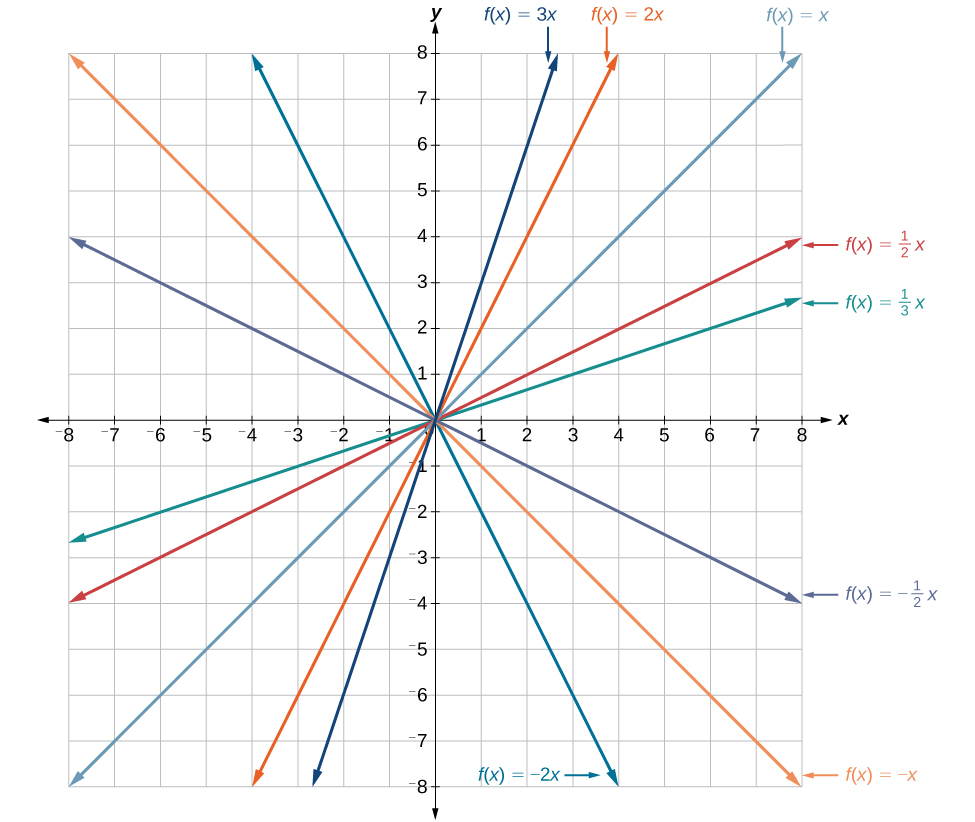
Desplazamiento vertical

En\(f(x)=mx+b\), el\(b\) actúa como el desplazamiento vertical, moviendo la gráfica hacia arriba y hacia abajo sin afectar la pendiente de la línea. Observe en la Figura\(\PageIndex{6}\) que sumar un valor de\(b\) a la ecuación de\(f(x)=x\) desplaza la gráfica de\(f\) un total de\(b\) unidades hacia arriba si\(b\) es positiva y\(|b|\) unidades hacia abajo si\(b\) es negativa.

Figura\(\PageIndex{6}\): Esta gráfica ilustra los desplazamientos verticales de la función\(f(x)=x\).

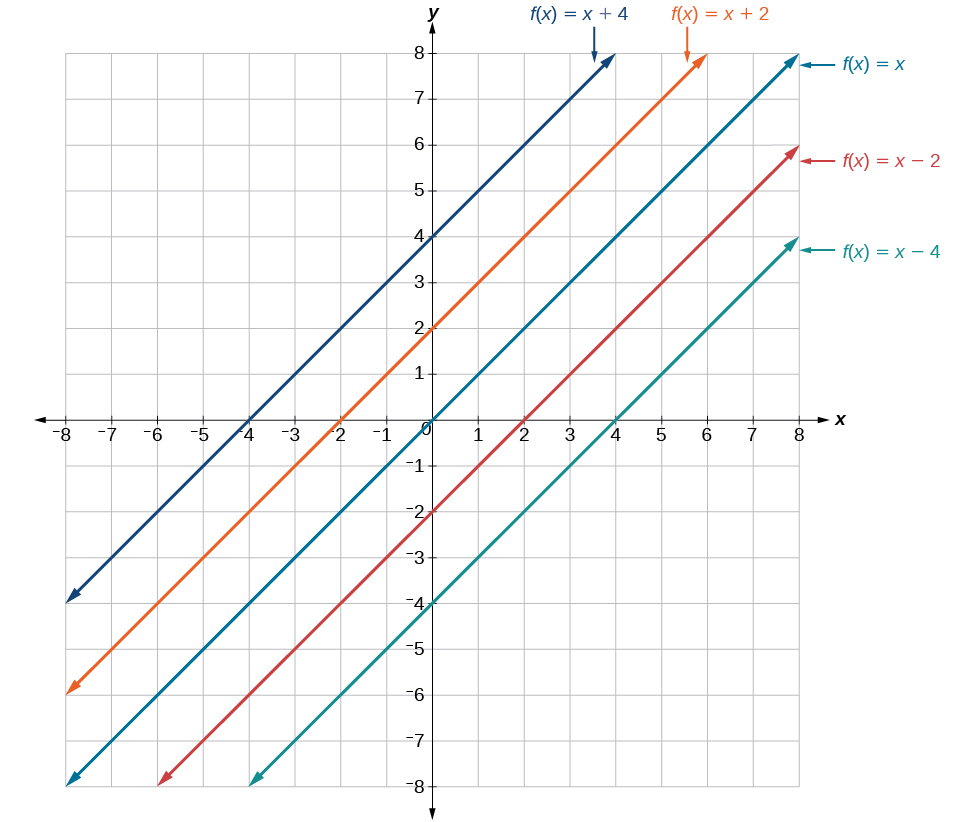
El uso de estiramientos verticales o compresiones junto con desplazamientos verticales es otra forma de ver la identificación de diferentes tipos de funciones lineales. Si bien esta puede no ser la forma más fácil de graficar este tipo de funciones, sigue siendo importante practicar cada método.

Dada la ecuación de una función lineal, utilice transformaciones para graficar la función lineal en la forma\(f(x)=mx+b\).

1. Gráfica\(f(x)=x\).
2. Estirar o comprimir verticalmente la gráfica por un factor\(m\).
3. Desplace la gráfica hacia arriba o hacia abajo de\(b\) las unidades.

Ejemplo\(\PageIndex{3}\)​​​​​​​: Graphing by Using Transformations

Gráfica\(f(x)=\frac{1}{2}x−3\) usando transformaciones.

Solución

La ecuación para la función muestra que\(m=\frac{1}{2}\) así la función de identidad es comprimida verticalmente por\(\frac{1}{2}\). La ecuación para la función también muestra que\(b=−3\) así la función de identidad se desplaza verticalmente hacia abajo 3 unidades. Primero, grafica la función de identidad y muestra la compresión vertical como en la Figura\(\PageIndex{7}\).

Figura\(\PageIndex{7}\): La función,\(y=x\), comprimida por un factor de\(\frac{1}{2}\).

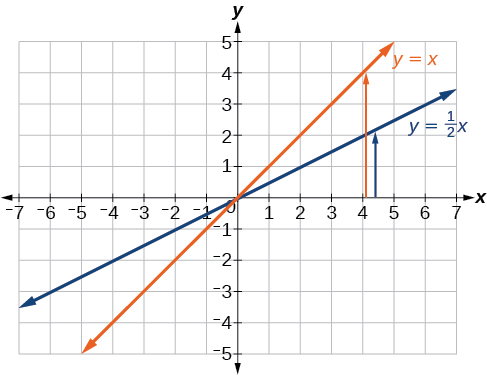
Después mostrar el desplazamiento vertical como en la Figura\(\PageIndex{8}\).

Figura\(\PageIndex{8}\): La función\(y=\frac{1}{2}x\), desplazada hacia abajo 3 unidades.

Ejercicio\(\PageIndex{3}\)

Gráfica\(f(x)=4+2x\), usando transformaciones.

Contestar

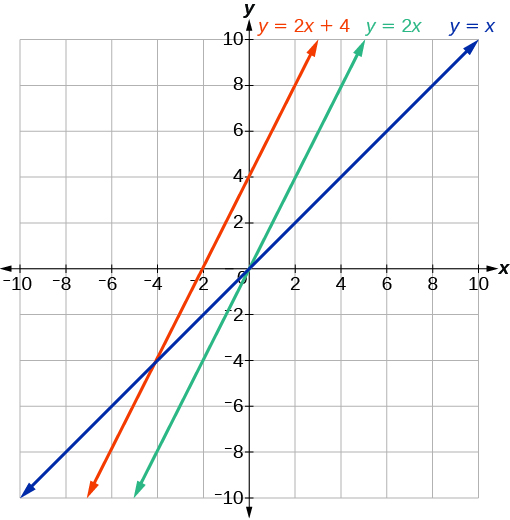
Figura\(\PageIndex{9}\)

En el Ejemplo 2.2.3, ¿podríamos haber esbozado la gráfica invirtiendo el orden de las transformaciones?

No. El orden de las transformaciones sigue el orden de las operaciones. Cuando la función se evalúa en una entrada dada, la salida correspondiente se calcula siguiendo el orden de las operaciones. Es por ello que realizamos primero la compresión. Por ejemplo, siguiendo el orden: Deja que la entrada sea 2.

\[\begin{align} f(2)&=\dfrac{1}{2}(2)-3 \\ &=1-3\\ &=-2 \end{align}\]

Escribir la Ecuación para una Función a partir de la Gráfica de una Línea

Recordemos que en Funciones Lineales, escribimos la ecuación para una función lineal a partir de una gráfica. Ahora podemos ampliar lo que sabemos sobre graficar funciones lineales para analizar las gráficas un poco más de cerca. Comienza por echar un vistazo a Figura\(\PageIndex{10}\). Podemos ver de inmediato que la gráfica cruza el eje y en el punto\((0, 4)\) por lo que esta es la intersección y.

Figura\(\PageIndex{10}\): Gráfica de una función lineal

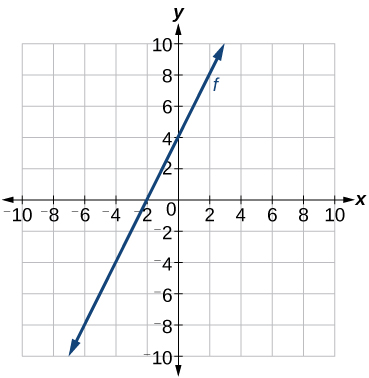
Entonces podemos calcular la pendiente encontrando el ascenso y la carrera. Podemos elegir dos puntos cualquiera, pero veamos el punto (−2,0). Para llegar de este punto a la intersección y, debemos subir 4 unidades (subir) y a la derecha 2 unidades (correr). Entonces la pendiente debe ser

\[m=\dfrac{\text{rise}}{\text{run}}=\dfrac{4}{2}=2\]

Sustituir la pendiente y la intersección y en la forma pendiente-intersección de una línea da

\[y=2x+4\]

Dada una gráfica de función lineal, encuentra la ecuación para describir la función.

1. Identificar la intercepción y de una ecuación.
2. Elija dos puntos para determinar la pendiente.
3. Sustituya la intersección y y la pendiente en la forma pendiente-intersección de una línea.

Ejemplo\(\PageIndex{4}\)​​​​​​​: Matching Linear Functions to Their Graphs

Coincidir cada ecuación de las funciones lineales con una de las líneas de la Figura\(\PageIndex{11}\).

1. \(f(x)=2x+3\)
2. \(g(x)=2x−3\)
3. \(h(x)=−2x+3\)
4. \(j(x)=\frac{1}{2}x+3\)

Figura\(\PageIndex{11}\): Gráfica de cuatro funciones lineales

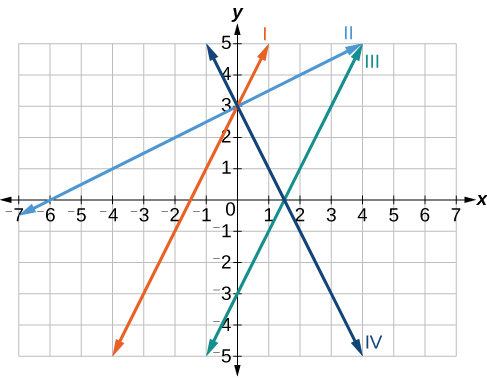
Solución

Analizar la información para cada función.

1. Esta función tiene una pendiente de 2 y una intersección en y de 3. Debe pasar por el punto\((0, 3)\) e inclinarse hacia arriba de izquierda a derecha. Podemos usar dos puntos para encontrar la pendiente, o podemos compararla con las otras funciones listadas. La función\(g\) tiene la misma pendiente, pero una intersección y diferente. Las líneas I y III tienen la misma inclinación porque tienen la misma pendiente. La línea III no pasa por\((0, 3)\) lo que\(f\) debe estar representada por la línea I.
2. Esta función también tiene una pendiente de 2, pero una intersección y de −3. Debe pasar por el punto\((0,−3)\) e inclinarse hacia arriba de izquierda a derecha. Debe estar representado por la línea III.
3. Esta función tiene una pendiente de —2 y una intersección y de 3. Esta es la única función listada con pendiente negativa, por lo que debe ser representada por la línea IV porque se inclina hacia abajo de izquierda a derecha.
4. Esta función tiene una pendiente de\(\frac{1}{2}\) y una intersección y de 3. Debe pasar por el punto (0, 3) e inclinarse hacia arriba de izquierda a derecha. Las líneas I y II pasan\((0, 3)\), pero la pendiente de\(j\) es menor que la pendiente de\(f\) por lo que la línea para\(j\) debe ser más plana. Esta función está representada por la Línea II.

Ahora podemos volver a etiquetar las líneas como en la Figura\(\PageIndex{12}\).

Figura\(\PageIndex{12}\)

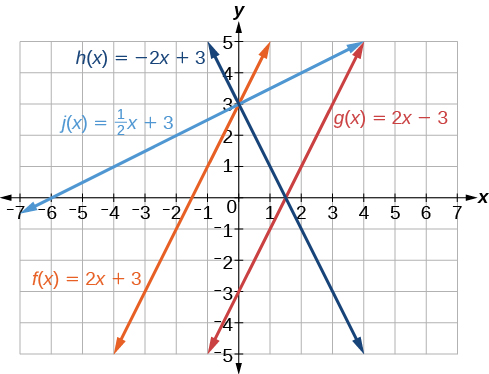
Encontrar la intercepción x de una línea

Hasta el momento, hemos estado encontrando las intercepciones y de una función: el punto en el que la gráfica de la función cruza el eje y. Una función también puede tener una intercepción x, que es la coordenada x del punto donde la gráfica de la función cruza el eje x. En otras palabras, es el valor de entrada cuando el valor de salida es cero.

Para encontrar la intercepción x, establezca una función\(f(x)\) igual a cero y resuelva para el valor de\(x\). Por ejemplo, considere la función que se muestra.

\[f(x)=3x−6\]

Establezca la función igual a 0 y resuelva para\(x\).

\[\begin{align} 0&=3x-6 \\ 6&=3x \\ 2&=x \\ x&=2 \end{align}\]

La gráfica de la función cruza el eje x en el punto\((2, 0)\).

¿Todas las funciones lineales tienen intercepciones x?

Figura\(\PageIndex{13}\).

Figura\(\PageIndex{13}\): Gráfica de\(y= 5\).

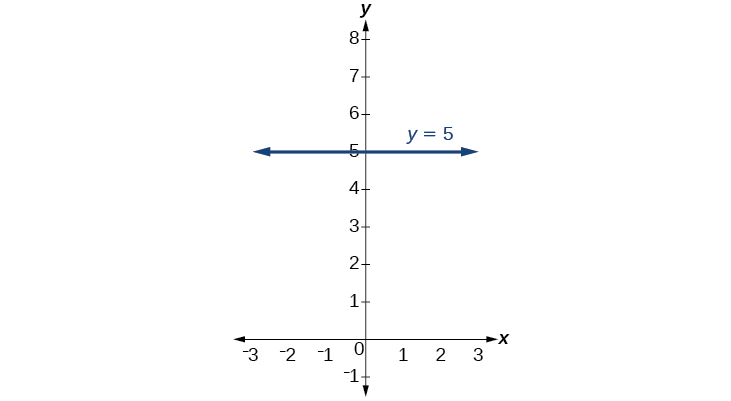
Nota: x-intercept

La intercepción x de la función es el valor de\(x\) cuando\(f(x)=0\). Se puede resolver mediante la ecuación\(0=mx+b\).

Ejemplo\(\PageIndex{5}\)​​​​​​​: Finding an x-intercept

Encuentra la intercepción x de\(f(x)=\frac{1}{2}−3\).

Solución

Establezca la función igual a cero para resolver\(x\).

\[\begin{align*} 0&=\dfrac{1}{2}x-3 \\ 3&=\dfrac{1}{2}x \\ 6 &= x \\ x&=6 \end{align*}\]

La gráfica cruza el eje x en el punto\((6, 0)\).

Análisis

En la Figura se muestra una gráfica de la función\(\PageIndex{14}\). Podemos ver que la intercepción x es\((6, 0)\) como esperábamos.

Figura\(\PageIndex{14}\): La gráfica de la función lineal\(f(x)=\frac{1}{2}x−3\).

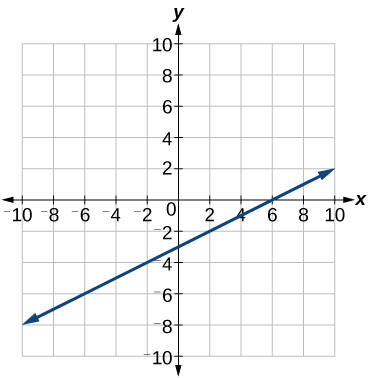
Ejercicio\(\PageIndex{5}\)

Encuentra la intercepción x de\(f(x)=\frac{1}{4}x−4\).

Contestar

\((16, 0)\)

Describiendo Líneas Horizontales y Verticales

Hay dos casos especiales de líneas en un gráfico: líneas horizontales y verticales. Una línea horizontal indica una salida constante, o valor y. En la Figura\(\PageIndex{15}\), vemos que la salida tiene un valor de 2 por cada valor de entrada. El cambio en salidas entre dos puntos cualesquiera, por lo tanto, es 0. En la fórmula de pendiente, el numerador es 0, por lo que la pendiente es 0. Si usamos\(m=0\) en la ecuación\(f(x)=mx+b\), la ecuación simplifica a\(f(x)=b\). En otras palabras, el valor de la función es una constante. Esta gráfica representa la función\(f(x)=2\).

Figura\(\PageIndex{15}\): Una línea horizontal que representa la función\(f(x)=2\).

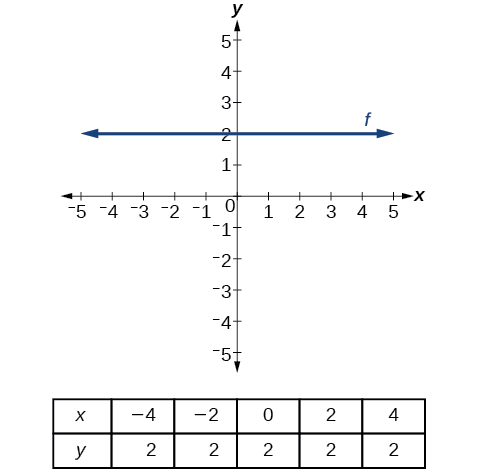
Una línea vertical indica una entrada constante, o valor x. Podemos ver que el valor de entrada para cada punto de la línea es 2, pero el valor de salida varía. Debido a que este valor de entrada se asigna a más de un valor de salida, una línea vertical no representa una función. Observe que entre dos puntos cualesquiera, el cambio en los valores de entrada es cero. En la fórmula de pendiente, el denominador será cero, por lo que la pendiente de una línea vertical es indefinida.

Figura\(\PageIndex{16}\)

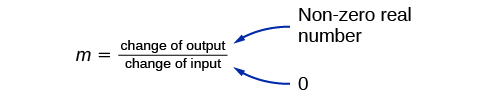
Observe que una línea vertical, como la de la Figura\(\PageIndex{17}\), tiene una intersección x, pero no una intersección en Y a menos que sea la línea\(x=0\). Esta gráfica representa la línea\(x=2\).

Figura\(\PageIndex{17}\): La línea vertical\(x=2\),, que no representa una función.

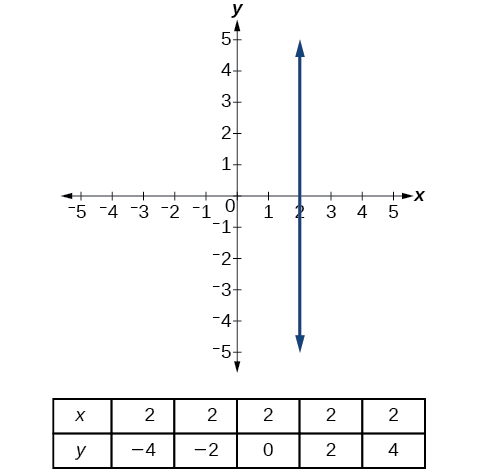
Definiciones: Líneas horizontales y verticales

Las líneas pueden ser horizontales o verticales.

• Una línea horizontal es una línea definida por una ecuación en la forma\(f(x)=b\).
• Una línea vertical es una línea definida por una ecuación en la forma\(x=a\).

Ejemplo\(\PageIndex{6}\)​​​​​​​: Writing the Equation of a Horizontal Line

Escribe la ecuación de la línea graficada en la Figura\(\PageIndex{18}\).

Figura\(\PageIndex{18}\): Gráfica de\(x=7\).

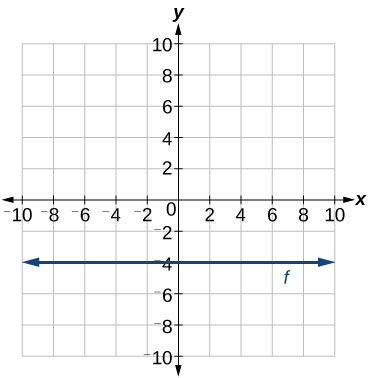
Solución

Para cualquier valor x, el valor y es −4, entonces la ecuación es\(y=−4\).

Ejemplo\(\PageIndex{7}\): Writing the Equation of a Vertical Line

Escribe la ecuación de la línea graficada en la Figura\(\PageIndex{19}\).

Figura\(\PageIndex{19}\): Gráfica de una línea vertical

Solución

El valor x constante es 7, por lo que la ecuación es\(x=7\).

Determinar si las líneas son paralelas o perpendiculares

Las dos líneas de la Figura\(\PageIndex{20}\) son líneas paralelas: nunca se cruzarán. Observe que tienen exactamente la misma pendiente, lo que significa que sus pendientes son idénticas. La única diferencia entre las dos líneas es la intersección y. Si desplazamos una línea verticalmente hacia la intersección y de la otra, se convertirían en la misma línea.

\ (y= - (2/3) x +7. Observe que son líneas paralelas.” src=” https://math.libretexts.org/@api/dek...02_02_019n.jpg "/>

Figura\ (\ PageIndex {20}\): Líneas paralelas.

Podemos determinar a partir de sus ecuaciones si dos líneas son paralelas comparando sus pendientes. Si las pendientes son las mismas y las intercepciones y son diferentes, las líneas son paralelas. Si las pendientes son diferentes, las líneas no son paralelas.

\(\PageIndex{21}\)Las figuras son perpendiculares.

Figura\(\PageIndex{21}\): Líneas perpendiculares.

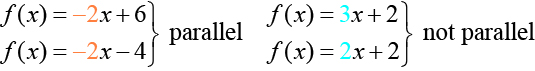
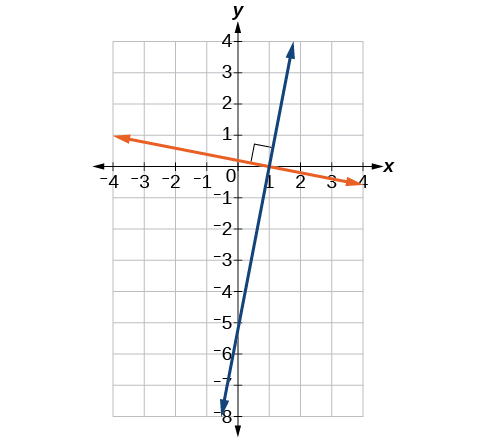
Las líneas perpendiculares no tienen la misma pendiente. Las pendientes de las líneas perpendiculares son diferentes entre sí de una manera específica. La pendiente de una línea es el recíproco negativo de la pendiente de la otra línea. El producto de un número y su recíproco es 1. Entonces, si\(m_1\) y\(m_2\) son recíprocos negativos el uno del otro, se pueden multiplicar juntos para rendir —1.

\[m_1m_2=−1\]

Para encontrar el recíproco de un número, divida 1 por el número. Entonces el recíproco de 8 es\(\frac{1}{8}\), y el recíproco de\(\frac{1}{8}\) es 8. Para encontrar el recíproco negativo, primero encuentra el recíproco y luego cambia el signo.

Al igual que con las líneas paralelas, podemos determinar si dos líneas son perpendiculares comparando sus pendientes, asumiendo que las líneas no son ni horizontales ni perpendiculares. La pendiente de cada línea inferior es el recíproco negativo de la otra por lo que las líneas son perpendiculares.

\[\begin{align} f(x)&=\dfrac{1}{4}x+2 &\text{negative reciprocal of $\dfrac{1}{4}$ is -4} \\ f(x)&=-4x+3 &\text{negative reciprocal of -4 is $\dfrac{1}{4}$} \end{align}\]

El producto de las pendientes es —1.

\[−4\Big(\dfrac{1}{4}\Big)=−1\]

Definiciones: Líneas paralelas y perpendiculares

Dos líneas son líneas paralelas si no se cruzan. Las pendientes de las líneas son las mismas.

\(f(x)=m_1x+b_1\)y\(g(x)=m_2x+b_2\) son paralelos si\(m_1 = m_2\).

Si y sólo si\(b_1=b_2\) y\(m_1=m_2\), decimos que las líneas coinciden. Las líneas coincidentes son la misma línea.

Dos líneas son líneas perpendiculares si se cruzan en ángulo recto.

\(f(x)=m_1x+b_1\)y\(g(x)=m_2x+b_2\) son perpendiculares si\(m_1m_2=−1\), y así\(m_2=\dfrac{−1}{m_1}\).

Ejemplo\(\PageIndex{8}\)​​​​​​​: Identifying Parallel and Perpendicular Lines

Dadas las siguientes funciones, identificar las funciones cuyas gráficas son un par de líneas paralelas y un par de líneas perpendiculares.

\[\begin{align} f(x)&=2x+3 & h(x)&=-2x+2 \\ g(x)&=\dfrac{1}{2}x-4 & f(x)&=2x-6 \end{align}\]

Solución

Las líneas paralelas tienen la misma pendiente. Debido a que las funciones\(f(x)=2x+3\) y\(j(x)=2x−6\) cada una tienen una pendiente de 2, representan líneas paralelas. Las líneas perpendiculares tienen pendientes recíprocas negativas. Debido a que −2 y\(\frac{1}{2}\) son recíprocos negativos, las ecuaciones,\(g(x)=\frac{1}{2}x−4\) y\(h(x)=−2x+2\) representan líneas perpendiculares.

Análisis

En la Figura se muestra una gráfica de las líneas\(\PageIndex{22}\).

Figura\(\PageIndex{22}\): Gráfico de\(h(x)\) (azul),\(f(x)\) (naranja),\(j(x)\) (verde) y\(g(x)\) (rojo)

La gráfica muestra que las líneas\(f(x)=2x+3\) y\(j(x)=2x–6\) son paralelas, y las líneas\(g(x)=\frac{1}{2}x–4\) y\(h(x)=−2x+2\) son perpendiculares.

Escribir la ecuación de una línea paralela o perpendicular a una línea dada

Si conocemos la ecuación de una línea, podemos usar lo que sabemos de pendiente para escribir la ecuación de una línea que sea paralela o perpendicular a la línea dada.

Escritura de Ecuaciones de Líneas Paralelas

Supongamos por ejemplo, se nos da la siguiente ecuación.

\[f(x)=3x+1 \nonumber\]

Sabemos que la pendiente de la línea formada por la función es 3. También sabemos que la intercepción y es\((0,1)\). Cualquier otra línea con una pendiente de 3 será paralela a\(f(x)\). Por lo que las líneas formadas por todas las siguientes funciones serán paralelas a\(f(x)\).

\[\begin{align*} g(x)&=3x+6 \\ h(x)&=3x+1\\ p(x)&=3x+\dfrac{2}{3} \end{align*}\]

Supongamos entonces que queremos escribir la ecuación de una línea que sea paralela\(f\) y que pase por el punto\((1, 7)\). Ya sabemos que la pendiente es de 3. Solo necesitamos determinar qué valor para\(b\) dará la línea correcta. Podemos comenzar con la forma punto-pendiente de una ecuación para una línea, y luego reescribirla en la forma pendiente-intersección.

\[\begin{align*} y−y_1&=m(x−x_1) \\ y−7&=3(x−1) \\ y−7&=3x−3 \\ y&=3x+4 \end{align*}\]

Así\(g(x)=3x+4\) es paralelo\(f(x)=3x+1\) y pasa por el punto\((1, 7)\).

Cómo...

Dada la ecuación de una función y un punto por el que pasa su gráfica, escribir la ecuación de una línea paralela a la línea dada que pasa por el punto dado.

1. Encuentra la pendiente de la función.
2. Sustituya los valores dados en la ecuación general de punto-pendiente o en la ecuación pendiente-intersección por una línea.
3. Simplificar.

Ejemplo\(\PageIndex{9}\): Finding a Line Parallel to a Given Line

Encuentra una línea paralela a la gráfica de\(f(x)=3x+6\) que pasa por el punto\((3, 0)\).

Solución

La pendiente de la línea dada es 3. Si elegimos la forma pendiente-intercepción, podemos sustituirla\(m=3\)\(x=3\), y\(f(x)=0\) en la forma pendiente-intercepción para encontrar la intersección y.

\[\begin{align*} g(x)&=3x+b \\ 0&=3(3)+b \\ b&=-9 \end{align*}\]

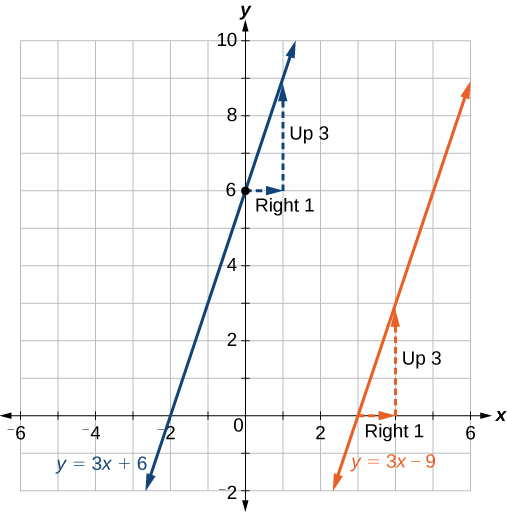
La línea paralela a la\(f(x)\) que pasa\((3,0)\) es\(g(x)=3x−9\).

Análisis

Podemos confirmar que las dos líneas son paralelas graficándolas. La figura\(\PageIndex{23}\) muestra que las dos líneas nunca se cruzarán.

Figura\(\PageIndex{23}\): Gráfica de dos funciones donde está la línea azul\(y=3x+6\), y la línea naranja está\(y=3x-9\).

Escritura de ecuaciones de líneas perpendiculares

Podemos usar un proceso muy similar para escribir la ecuación para una línea perpendicular a una línea dada. Sin embargo, en lugar de usar la misma pendiente, usamos el recíproco negativo de la pendiente dada. Supongamos que se nos da la siguiente función:

\[f(x)=2x+4 \nonumber\]

La pendiente de la línea es 2, y su recíproco negativo es\(−\frac{1}{2}\). Cualquier función con pendiente de\(−\frac{1}{2}\) será perpendicular a\(f(x)\). Por lo que las líneas formadas por todas las siguientes funciones serán perpendiculares a\(f(x)\).

\[\begin{align*} g(x)&=-\dfrac{1}{2}x+4 \\[4pt] h(x)&=-\dfrac{1}{2}x+2 \\[4pt] p(x)&=-\dfrac{1}{2}x-\dfrac{1}{2} \end{align*}\]

Como antes, podemos reducir nuestras opciones para una línea perpendicular particular si sabemos que pasa por un punto dado. Supongamos entonces que queremos escribir la ecuación de una línea que es perpendicular\(f(x)\) y pasa por el punto\((4, 0)\). Ya sabemos que la pendiente es\(−\frac{1}{2}\). Ahora podemos usar el punto para encontrar la intersección y sustituyendo los valores dados en la forma pendiente-intercepción de una línea y resolviendo para\(b\).

\[\begin{align*} g(x)&=mx+b \\[4pt] 0&=-\dfrac{1}{2}(4)+b \\[4pt] 0 & = -2+b\\[4pt] 2&=b \\ b&=2 \end{align*}\]

La ecuación para la función con una pendiente de\(−\frac{1}{2}\) y una intersección y de 2 es

\[g(x)=−\dfrac{1}{2}x+2\]

Así\(g(x)=−\frac{1}{2}x+2\) es perpendicular\(f(x)=2x+4\) y pasa por el punto\((4, 0)\). Tenga en cuenta que las líneas perpendiculares pueden no verse obviamente perpendiculares en una calculadora gráfica a menos que utilicemos la función de zoom cuadrado.

Una línea horizontal tiene una pendiente de cero y una línea vertical tiene una pendiente indefinida. Estas dos líneas son perpendiculares, pero el producto de sus pendientes no es —1. ¿Este hecho no contradice la definición de líneas perpendiculares?

No. Para dos funciones lineales perpendiculares, el producto de sus pendientes es —1. Sin embargo, una línea vertical no es una función por lo que la definición no se contradice.

Cómo...

Dada la ecuación de una función y un punto por el que pasa su gráfica, escribir la ecuación de una línea perpendicular a la línea dada.

1. Encuentra la pendiente de la función.
2. Determinar el recíproco negativo de la pendiente.
3. Sustituya la nueva pendiente y los valores para\(x\) y\(y\) desde el par de coordenadas proporcionado en\(g(x)=mx+b\).
4. Resolver para\(b\).
5. Escribe la ecuación para la línea.

Ejemplo\(\PageIndex{10}\): Finding the Equation of a Perpendicular Line

Encuentra la ecuación de una línea perpendicular a la\(f(x)=3x+3\) que pasa por el punto\((3, 0)\).

Solución

La línea original tiene pendiente\(m=3\), por lo que la pendiente de la línea perpendicular será su recíproco negativo, o\(−\frac{1}{3}\). Usando esta pendiente y el punto dado, podemos encontrar la ecuación para la línea.

\[\begin{align*} g(x)&= \; –\dfrac{1}{3}x+b \\[4pt] 0&= \; –\dfrac{1}{3}(3)+b \\[4pt] 1&=b \\ b&=1 \end{align*}\]

La línea perpendicular a la\(f(x)\) que pasa\((3, 0)\) es\(g(x)=−\frac{1}{3}x+1\).

Análisis

Una gráfica de las dos líneas se muestra en la Figura\(\PageIndex{24}\) a continuación.

\ (f (x)\) = 3x + 6.” src=” https://math.libretexts.org/@api/dek...02_02_023n.jpg "/>

Figura\(\PageIndex{24}\): Gráfica de dos funciones donde está la línea azul\(g(x)= -\frac{1}{3}x+1\), y la línea naranja está\(f(x)=3x+6\).

Ejercicio\(\PageIndex{5}\)

Dada la función\(h(x)=2x−4\), escribir una ecuación para la línea que pasa a través de la\((0,0)\) que es

1. paralelo a\(h(x)\)
2. perpendicular a\(h(x)\)

Contestar

\(f(x)=2x\)\(g(x)=−\frac{1}{2}x\)

Cómo...

Dados dos puntos en una línea y un tercer punto, escribir la ecuación de la línea perpendicular que pasa por el punto.

1. Determinar la pendiente de la línea que pasa por los puntos.
2. Encuentra el recíproco negativo de la pendiente.
3. Utilice la forma pendiente-intersección o la forma punto-pendiente para escribir la ecuación sustituyendo los valores conocidos.
4. Simplificar.

Ejemplo\(\PageIndex{11}\): Finding the Equation of a Line Perpendicular to a Given Line Passing through a Point

Una línea pasa por los puntos\((−2, 6)\) y\((4,5)\). Encuentra la ecuación de una línea perpendicular que pasa por el punto\((4,5)\).

A partir de los dos puntos de la línea dada, podemos calcular la pendiente de esa línea.

\[\begin{align*} m_1&=\dfrac{5-6}{4−(−2)} \\ &=\dfrac{-1}{6} \\ &=−\dfrac{1}{6} \end{align*}\]

Encuentra el recíproco negativo de la pendiente.

\[\begin{align*} m_2&=\dfrac{-1}{-\dfrac{1}{6}} \\ &=−1\Big(−\dfrac{6}{1}\Big) \\ & =6 \end{align*}\]

Entonces podemos resolver para la intersección y de la línea que pasa por el punto\((4,5)\).

\[\begin{align*} g(x)&=6x+b \\ 5&=6(4)+b \\ 5&=24+b \\ −19&=b \\ b&=−19 \end{align*}\]

La ecuación para la línea que es perpendicular a la línea que pasa por los dos puntos dados y también pasa a través del punto\((4,5)\) es

\[y=6x−19 \nonumber\]

Ejercicio\(\PageIndex{1}\)

Una línea pasa por los puntos,\((−2,−15)\) y\((2,−3)\). Encuentra la ecuación de una línea perpendicular que pasa por el punto,\((6,4)\).

Contestar

\(y= \; –\dfrac{1}{3}x+6\)

Resolver un Sistema de Ecuaciones Lineales Usando una Gráfica

Un sistema de ecuaciones lineales incluye dos o más ecuaciones lineales. Las gráficas de dos líneas se cruzarán en un solo punto si no son paralelas. Dos líneas paralelas también pueden cruzarse si son coincidentes, lo que significa que son la misma línea y se cruzan en cada punto. Para dos líneas que no son paralelas, el único punto de intersección satisfará ambas ecuaciones y por lo tanto representará la solución al sistema.

Para encontrar este punto cuando las ecuaciones se dan como funciones, podemos resolver para un valor de entrada para que\(f(x)=g(x)\). En otras palabras, podemos establecer las fórmulas para las líneas iguales entre sí, y resolver para la entrada que satisfaga la ecuación.

Ejemplo\(\PageIndex{12}\): Finding a Point of Intersection Algebraically

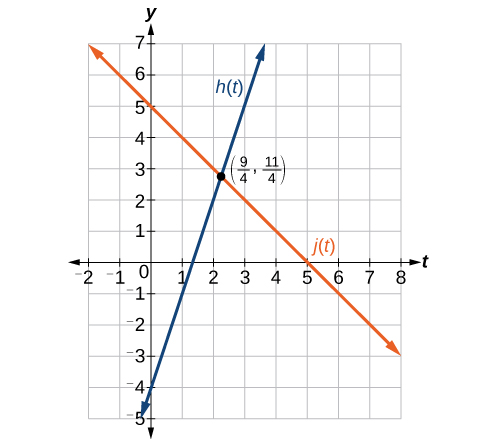
Encuentra el punto de intersección de las líneas\(h(t)=3t−4\) y\(j(t)=5−t\).

Solución

Set\(h(t)=j(t)\).

\[\begin{align} 3t-4&=5-t \\ 4t&=9 \\ t&=\dfrac{9}{4} \end{align}\]

Esto nos dice que las líneas se cruzan cuando la entrada es\(\frac{9}{4}\).

Luego podemos encontrar el valor de salida del punto de intersección evaluando cualquiera de las funciones en esta entrada.

\[\begin{align} j\Big( \dfrac{9}{4} \Big)&=5-\dfrac{9}{4} \\ &= \dfrac{11}{4}\end{align}\]

Estas líneas se cruzan en el punto\(\Big(\frac{9}{4},\frac{11}{4}\Big)\).

Análisis

Al mirar Figura\(\PageIndex{25}\), este resultado parece razonable.

Figura\(\PageIndex{25}\): Gráfica de dos funciones\(h(t) = 3t - 4\)\(j(t)=t +5\) y su intersección en\((\frac{9}{4},\frac{11}{4})\).

Si nos pidieran encontrar el punto de intersección de dos líneas paralelas distintas, ¿algo en el proceso de solución nos alertaría de que no hay soluciones?

Sí. Después de establecer las dos ecuaciones iguales entre sí, el resultado sería la contradicción “\(0 = \text{non-zero real number}\)”.

Ejercicio\(\PageIndex{7}\)

Mire la gráfica en la Figura\(\PageIndex{23}\) e identifique lo siguiente para la función\(j(t):\)

1. interceptar en y
2. intercepción (s) x
3. talud
4. ¿Es\(j(t)\) paralelo o perpendicular a\(h(t)\) (o ninguno)?
5. ¿Es\(j(t)\) una función creciente o decreciente (o ninguna)?
6. Escriba una descripción de transformación para\(j(t)\) desde la función del kit de herramientas de identidad\(f(x)=x\).

Contestar

1. \((0,5)\)
2. (5, 0)
3. Talud -1
4. Ni paralelo ni perpendicular
5. Función decreciente
6. Dada la función de identidad, realizar un volteo vertical (sobre el eje t) y desplazar hacia arriba 5 unidades.

Ejemplo\(\PageIndex{13}\): Finding a Break-Even Point

Una empresa vende cascos deportivos. La compañía incurre en un costo fijo único por $250,000. Cada casco cuesta $120 para producir, y se vende por $140.

1. Encuentra la función costo,\(C\), para producir\(x\) cascos, en dólares.
2. Encuentra la función de ingresos\(R\),, de las ventas de\(x\) cascos, en dólares.
3. Encuentra el punto de equilibrio, el punto de intersección de las dos gráficas\(C\) y\(R\).

Solución

a. La función de costo en la suma del costo fijo, $125,000, y el costo variable, $120 por casco.

\(C(x)=120x+250,000\)

b. La función de ingresos es el ingreso total de la venta de\(x\) cascos,\(R(x)=140x\).

c. El punto de equilibrio es el punto de intersección de la gráfica de las funciones de costo e ingresos. Para encontrar la coordenada x del par de coordenadas del punto de intersección, establezca las dos ecuaciones iguales y resuelva para\(x\).

\[\begin{align*} C(x)&=R(x) \\ 250,000+120x&=140x \\ 250,000&=20x \\ x&=12,500 \end{align*}\]

Para encontrar\(y\), evaluar ya sea la función de ingresos o costo en 12,500.

\[\begin{align*} R(20)&=140(12,500) \\ &=$1,750,000 \end{align*}\]

El punto de equilibrio es\((12,500,1,750,000)\).

Análisis

Esto significa que si la compañía vende 12 mil 500 cascos, se equiparan; tanto las ventas como el costo incurrido igualaron 1.75 millones de dólares. Ver Figura\(\PageIndex{26}\).

Figura\(\PageIndex{26}\): Gráfica de las dos funciones,\(C(x)\) y\(R(x)\) donde se muestra que por debajo de\((12500, 1750000)\) la empresa pierde dinero y por encima de ese punto la empresa obtiene ganancias.

Conceptos clave

• Las funciones lineales se pueden graficar trazando puntos o usando la intersección y y la pendiente.
• Las gráficas de funciones lineales pueden transformarse mediante el uso de cambios hacia arriba, abajo, izquierda o derecha, así como a través de estiramientos, compresiones y reflexiones.
• La intersección y y la pendiente de una línea se pueden usar para escribir la ecuación de una línea.
• La intersección x es el punto en el que la gráfica de una función lineal cruza el eje x.
• Las líneas horizontales están escritas en la forma,\(f(x)=b\).
• Las líneas verticales están escritas en la forma,\(x=b\).
• Las líneas paralelas tienen la misma pendiente.
• Las líneas perpendiculares tienen pendientes recíprocas negativas, asumiendo que ninguna es vertical.
• Una línea paralela a otra línea, pasando por un punto dado, se puede encontrar sustituyendo el valor de pendiente de la línea y los valores x e y del punto dado en la ecuación\(f(x)=mx+b\), y usando los resultados\(b\) que se obtienen. Del mismo modo, también se puede utilizar la forma punto-pendiente de una ecuación.
• Una línea perpendicular a otra línea, pasando por un punto dado, se puede encontrar de la misma manera, con la excepción de utilizar la pendiente recíproca negativa.
• Se puede resolver un sistema de ecuaciones lineales estableciendo las dos ecuaciones iguales entre sí y resolviendo para\(x\). El valor y se puede encontrar evaluando cualquiera de las ecuaciones originales usando este valor x.
• Un sistema de ecuaciones lineales también se puede resolver encontrando el punto de intersección en una gráfica.

Glosario

línea horizontal
una línea definida por\(f(x)=b\), donde\(b\) es un número real. La pendiente de una línea horizontal es 0.

líneas paralelas
dos o más líneas con la misma pendiente

líneas perpendiculares
dos líneas que se cruzan en ángulo recto y tienen pendientes que son recíprocas negativas entre sí

línea vertical
una línea definida por\(x=a\), donde a es un número real. La pendiente de una línea vertical es indefinida.

x-interceptar
el punto en la gráfica de una función lineal cuando el valor de salida es 0; el punto en el que la gráfica cruza el eje horizontal