2.E: Funciones Lineales (Ejercicios)
- Page ID
- 121529
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)2.1 Funciones lineales
Verbal
1) Terry está esquiando por una colina empinada. La elevación de Terry,\(E(t)\), en pies después de\(t\) segundos viene dada por\(E(t)=3000−70t\). Escribe una oración completa describiendo la elevación inicial de Terry y cómo está cambiando con el tiempo.
- Contestar
-
Terry comienza a una elevación de\(3000\) pies y desciende\(70\) pies por segundo.
2) María está escalando una montaña. La elevación de María,\(E(t)\), en pies después de\(t\) minutos viene dada por\(E(t)=1200+40t\). Escribe una oración completa describiendo la elevación inicial de María y cómo está cambiando con el tiempo.
3) Jessica está caminando a casa desde la casa de un amigo. Después de\(2\) minutos está\(1.4\) a kilómetros de casa. Doce minutos después de irse, está\(0.9\) a kilómetros de su casa. ¿Cuál es su tarifa en millas por hora?
- Contestar
-
\(3\)millas por hora
4) Sonya se encuentra actualmente\(10\) a millas de casa y está caminando más lejos a\(2\) millas por hora. Escribe una ecuación para su distancia de casa\(t\) horas a partir de ahora.
5) Un barco está a\(100\) millas de distancia del puerto deportivo, navegando directamente hacia él a\(10\) millas por hora. Escribir una ecuación para la distancia de la embarcación desde el puerto deportivo después de\(t\) horas.
- Contestar
-
\(d(t) =100−10t\)
6) Timmy va a la feria con\(\$40\). Cada viaje cuesta\(\$2\). ¿Cuánto dinero le quedará después de montar\(n\) en bicicleta?
Algebraico
Para los ejercicios 7-14, determinar si la ecuación de la curva se puede escribir como una función lineal.
7)\(y= \dfrac{1}{4}x+6\)
- Contestar
-
Sí
8)\(y=3x−5\)
9)\(y=3 x^2 −2\)
- Contestar
-
No
10)\(3x+5y=15\)
11)\(3 x^2 +5y=15\)
- Contestar
-
No
12)\(3x+5 y^ 2 =15\)
13)\(−2 x^2 +3y^2 =6\)
- Contestar
-
No
14)\(−\dfrac{x−3}{5} =2y\)
Para los ejercicios 15-24, determinar si cada función está aumentando o disminuyendo.
15)\(f(x)=4x+3\)
- Contestar
-
Incrementando
16)\(g(x)=5x+6\)
17)\(a(x)=5−2x\)
- Contestar
-
Disminuyendo
18)\(b(x)=8−3x\)
19)\(h(x)=−2x+4\)
- Contestar
-
Disminuyendo
20)\(k(x)=−4x+1\)
21)\(j(x)=\dfrac{1}{2}x−3\)
- Contestar
-
Incrementando
22)\(p(x)=\dfrac{1}{4}x−5\)
23)\(n(x)=−\dfrac{1}{3}x−2\)
- Contestar
-
Disminuyendo
24)\(m(x)=−\dfrac{3}{8}x+3\)
Para los ejercicios 25-29, encuentra la pendiente de la línea que pasa por los dos puntos dados.
25)\((2, 4)\) y\((4, 10)\)
- Contestar
-
\(3\)
26)\((1, 5)\) y\((4, 11)\)
27)\((−1,4)\) y\((5,2)\)
- Contestar
-
\(–\dfrac{1}{3}\)
28)\((8,−2)\) y\((4,6)\)
29) (6, 11) y (−4, 3)
- Contestar
-
\(\dfrac{4}{5}\)
Para los ejercicios 30-37, dado cada conjunto de información, encontrar una ecuación lineal que satisfaga las condiciones, si es posible.
30)\(f(−5)=−4\), y\(f(5)=2\)
31)\(f(−1)=4\) y\(f(5)=1\)
- Contestar
-
\(f(x)=−\dfrac{1}{2}x+\dfrac{7}{2}\)
32)\((2,4)\) y\((4,10)\)
33) Pasa a través\((1,5)\) y\((4,11)\)
- Contestar
-
\(y=2x+3\)
34) Pasa a través\((−1, 4)\) y\((5, 2)\)
35) Pasa a través\((−2, 8)\) y\((4, 6)\)
- Contestar
-
\(y=−\dfrac{1}{3}x+\dfrac{22}{3}\)
36)\(x\) interceptar en (−2, 0) e\(y\) interceptar en (0, −3)
37)\(x\) interceptar en (−5, 0) e\(y\) interceptar en (0, 4)
- Contestar
-
\(y=\dfrac{4}{5}x+4\)
Gráfica
Para los ejercicios 38-,40 encuentra la pendiente de las líneas gráficas.
38)
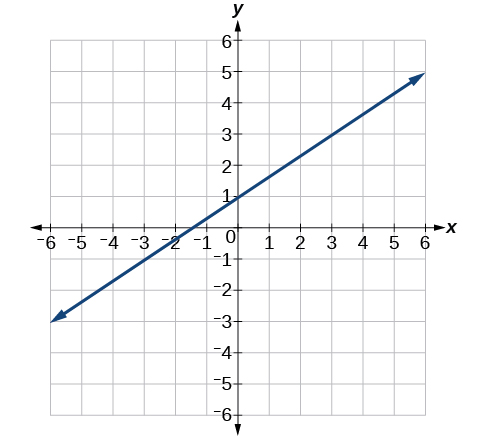
39)
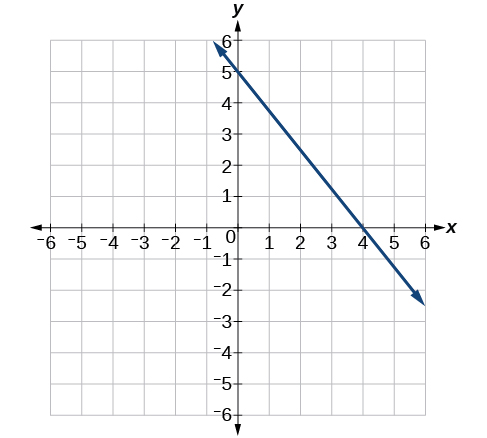
- Contestar
-
\(−\dfrac{5}{4}\)
40)
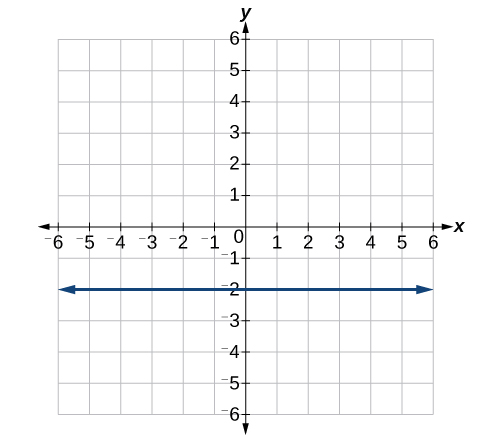
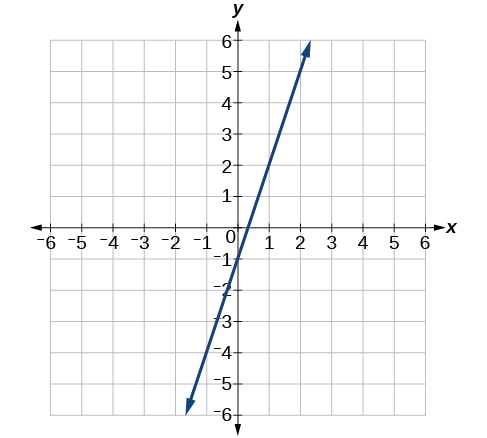
Para los ejercicios 41-46, escribir una ecuación para las líneas gráficas.
41)
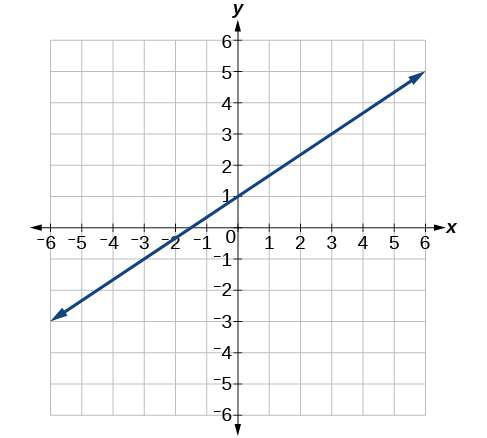
- Contestar
-
\(y= \dfrac{2}{3} x+1\)
42)
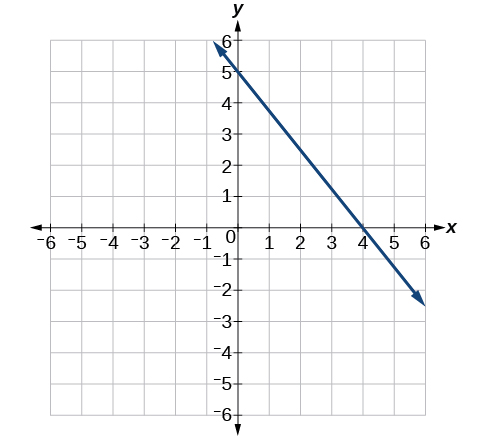
43)
- Contestar
-
\(y=−2x+3\)
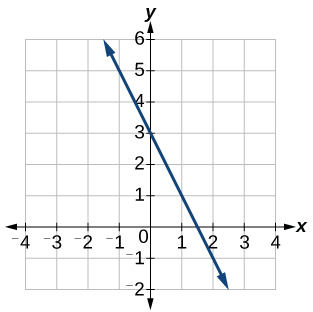
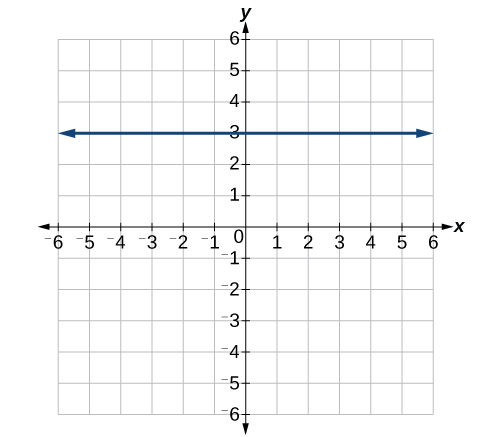
44)
45)
- Contestar
-
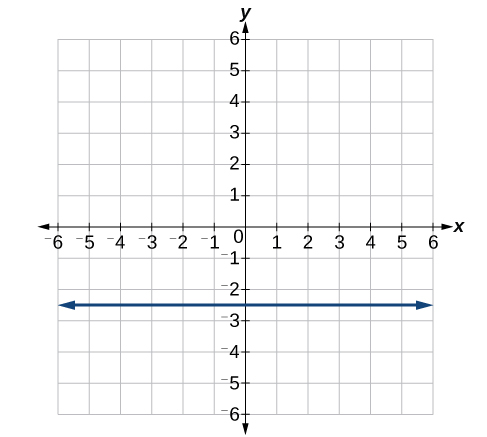
\(y=3\)
46)
Numérico
Para los ejercicios 47-51, ¿cuál de las tablas podría representar una función lineal? Para cada uno que pueda ser lineal, encuentre una ecuación lineal que modele los datos.
47)
| \(x\) | 0 | 5 | 10 | 15 |
|---|---|---|---|---|
| \(g(x)\) | 5 | —10 | —25 | —40 |
- Contestar
-
Lineal,\(g(x)=−3x+5\)
48)
| \(x\) | 0 | 5 | 10 | 15 |
|---|---|---|---|---|
| \(h(x)\) | 5 | 30 | 105 | 230 |
| \(x\) | 0 | 5 | 10 | 15 |
|---|---|---|---|---|
| \(f(x)\) | —5 | 20 | 45 | 70 |
- Contestar
-
Lineal,\(f(x)=5x−5\)
49)
| \(x\) | 5 | 10 | 20 | 25 |
|---|---|---|---|---|
| \(k(x)\) | 28 | 13 | 58 | 73 |
| \(x\) | 0 | 2 | 4 | 6 |
|---|---|---|---|---|
| \(g(x)\) | 6 | —19 | —44 | —69 |
- Contestar
-
Lineal,\(g(x)=−\dfrac{25}{2}x+6\)
50)
| \(x\) | 2 | 4 | 6 | 8 |
|---|---|---|---|---|
| \(f(x)\) | —4 | 16 | 36 | 56 |
| \(x\) | 2 | 4 | 6 | 8 |
|---|---|---|---|---|
| \(f(x)\) | —4 | 16 | 36 | 56 |
- Contestar
-
Lineal,\(f(x)=10x−24\)
51)
| \(x\) | 0 | 2 | 6 | 8 |
|---|---|---|---|---|
| \(k(x)\) | 6 | 31 | 106 | 231 |
Tecnología
52) Si\(f\) es una función lineal,\(f(0.1)=11.5\), y\(f(0.4)=–5.9\), encontrar una ecuación para la función.
- Contestar
-
\(f(x)=−58x+17.3\)
53) Graficar la función\(f\) en un dominio de\([ –10, 10 ]: f(x)=0.02x−0.01\). Ingresa la función en una utilidad gráfica. Para la ventana de visualización, establezca el valor mínimo de\(x\) a ser −10 y el valor máximo de\(x\) a ser 10.
54) Graficar la función\(f\) en un dominio de\([ –10, 10 ]:fx)=2,500x+4,000\)
- Contestar
-
55) La Tabla siguiente muestra la entrada,\(w\), y salida,\(k\), para una función lineal\(k\).
- Rellene los valores faltantes de la tabla.
- Escribe la función lineal\(k\), redondear a\(3\) decimales.
| \(w\) | —10 | 5.5 | 67.5 | b |
|---|---|---|---|---|
| \(k\) | 30 | —26 | a | —44 |
56) La Tabla siguiente muestra la entrada,\(p\), y salida,\(q\), para una función lineal\(q\).
- Rellene los valores faltantes de la tabla.
- Escribe la función lineal\(k\).
| \(p\) | 0.5 | 0.8 | 12 | b |
|---|---|---|---|---|
| \(q\) | 400 | 700 | a | 1,000,000 |
- Contestar
-
- \(a=11\),900;\(b=1001.1\)
- \(q(p)=1000p−100\)
57) Graficar la función lineal\(f\) en un dominio de\([ −10,10 ]\) para la función cuya pendiente es\(\dfrac{1}{8}\) y es la intersección y\(\dfrac{31}{16}\). Etiquetar los puntos para los valores de entrada de\(−10\) y\(10\).
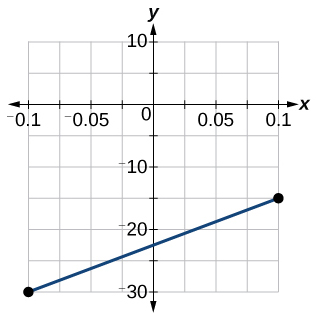
58) Graficar la función lineal\(f\) en un dominio de\([ −0.1,0.1 ]\) para la función cuya pendiente es\(75\) y\(y\) -interceptar es\(-22.5\). Etiquetar los puntos para los valores de entrada de\(-0.1\) y\(0.1\).
- Contestar
-
59) Graficar la función lineal\(f\) donde\(f(x)=ax+b\) en el mismo conjunto de ejes en un dominio de\([ −4,4 ]\) para los siguientes valores de\(a\) y\(b\).
- \(a=2;\)\(b=3\)
- \(a=2; \)\(b=4\)
- \(a=2;\)\(b=–4\)
- \(a=2;\)\(b=–5\)
Extensiones
60) Encuentra el valor de\(x\) si una función lineal pasa por los siguientes puntos y tiene la siguiente pendiente:\((x,2),(−4,6),\)\(m=3\)
- Contestar
-
\(x=−\dfrac{16}{3}\)
61) Encuentra el valor de\(y\) si una función lineal pasa por los siguientes puntos y tiene la siguiente pendiente:\((10,y),(25,100),\)\(m=−5\)
62) Encuentra la ecuación de la línea que pasa por los siguientes puntos:\((a, b)\) y\(( a, b+1 )\)
- Contestar
-
\(x=a\)
63) Encuentra la ecuación de la línea que pasa por los siguientes puntos:\((2a, b)\) y (a, b+1)
64) Encuentra la ecuación de la línea que pasa por los siguientes puntos:\((a, 0)\) y\((c, d)\)
- Contestar
-
\(y=\dfrac{d}{c−a}x−\dfrac{ad}{c−a}\)
Aplicaciones del mundo real
65) Al mediodía, una barista se da cuenta de que tiene\(\$20\) en su jarra de punta. Si hace un promedio\(\$0.50\) de cada cliente, ¿cuánto tendrá en su tarro de propinas si atiende a\(n\) más clientes durante su turno?
66) Una membresía de gimnasio con dos sesiones de entrenamiento personal cuesta\(\$125\), mientras que la membresía en el gimnasio con cinco sesiones de entrenamiento personal cuesta\(\$260\). ¿Cuál es el costo por sesión?
- Contestar
-
\(\$45\)por sesión de entrenamiento.
67) Un negocio de ropa encuentra que existe una relación lineal entre el número de camisas\(n\),, puede vender y el precio\(p\),, puede cobrar por camisa. En particular, los datos históricos muestran que las\(1,000\) camisas se pueden vender a un precio de\(\$30\), mientras que las\(3,000\) camisas se pueden vender a un precio de\(\$22\). Encuentra una ecuación lineal en la forma\(p(n)=mn+b\) que dé el precio\(p\) que pueden cobrar por las\(n\) camisas.
68) Una compañía telefónica cobra por el servicio de acuerdo a la fórmula:\(C(n)=24+0\) .1n, donde\(n\) está el número de minutos platicados, y\(C(n)\) es el cargo mensual, en dólares. Encuentra e interpreta la tasa de cambio y el valor inicial.
- Contestar
-
La tasa de cambio es\(0.1\). Por cada minuto adicional platicado, el cargo mensual aumenta en\(\$0.1\) o\(10\) centavos. El valor inicial es\(24\). Cuando no hay minutos platicados, inicialmente el cargo es\(\$24\).
69) Un agricultor encuentra que existe una relación lineal entre el número de tallos de frijol\(n\),, ella planta y el rendimiento,\(y\), cada planta produce. Cuando planta\(30\) tallos, cada planta produce\(30\) oz de frijoles. Cuando planta\(34\) tallos, cada planta produce\(28\) oz de frijoles. Encuentra una relación lineal en la forma\(y=mn+b\) que da el rendimiento cuando se plantan\(n\) tallos.
70) La población de una ciudad en el año 1960 era\(287,500\). En 1989 la población era\(275,900\). Calcular la tasa de crecimiento de la población y hacer una declaración sobre la tasa de cambio poblacional en las personas por año.
- Contestar
-
La pendiente es\(-400\). Esto significa que por cada año entre 1960 y 1989, la población descendió\(400\) por año en la ciudad.
71) La población de un pueblo ha ido creciendo linealmente. En 2003, la población era\(45,000\), y la población ha ido creciendo por\(1,700\) personas cada año. Escribir una ecuación,\(P(t)\), para la población\(t\) años posteriores a 2003.
72) Supongamos que el ingreso promedio anual (en dólares) para los años 1990 a 1999 viene dado por la función lineal:\(I(x)=1054x+23\),\(286,\) donde\(x\) está el número de años posteriores a 1990. ¿Cuál de los siguientes interpreta la pendiente en el contexto del problema?
- A partir de 1990, el ingreso promedio anual era\(\$23,286\).
- En el periodo de diez años comprendido entre 1990 y 1999, el ingreso promedio anual aumentó en un total de\(\$1,054\).
- Cada año en la década de los noventa, el ingreso promedio anual aumentó en 1.054 dólares.
- El ingreso promedio anual se elevó a un nivel de $23,286 a finales de 1999.
- Contestar
-
c
73) Cuando la temperatura es\(0\) grados Celsius, la temperatura Fahrenheit es\(32\). Cuando la temperatura Celsius es\(100\), la temperatura Fahrenheit correspondiente es\(212\). Expresar la temperatura Fahrenheit como una función lineal de\(C\), la temperatura Celsius,\(F(C)\).
- Encuentre la tasa de cambio de temperatura Fahrenheit por cada unidad de cambio de temperatura de Celsius.
- Encontrar e interpretar\(F(28)\).
- Encontrar e interpretar\(F(–40)\).
2.2 Gráficas de Funciones Lineales
Verbal
1) Si las gráficas de dos funciones lineales son paralelas, describa la relación entre las pendientes y las\(y\) -intercepciones.
- Contestar
-
Las pendientes son iguales;\(y\) -las intercepciones no son iguales.
2) Si las gráficas de dos funciones lineales son perpendiculares, describa la relación entre las pendientes y las\(y\) -intercepciones.
3) Si una línea horizontal tiene la ecuación\(f(x)=a\) y una línea vertical tiene la ecuación\(x=a\), ¿cuál es el punto de intersección? Explica por qué lo que encontraste es el punto de intersección.
- Contestar
-
El punto de intersección es\((a,a)\). Esto se debe a que para la línea horizontal, todas las\(y\) coordenadas son a y para la línea vertical, todas las\(x\) coordenadas son a. el punto de intersección tendrá estas dos características.
4) Explicar cómo encontrar una línea paralela a una función lineal que pasa por un punto dado.
5) Explicar cómo encontrar una línea perpendicular a una función lineal que pasa por un punto dado.
- Contestar
-
Primero, encuentra la pendiente de la función lineal. Entonces toma el recíproco negativo de la pendiente; esta es la pendiente de la línea perpendicular. Sustituir la pendiente de la línea perpendicular y la coordenada del punto dado en la ecuación\(y=mx+b\) y resolver para\(b\). Luego escribe la ecuación de la línea en la forma\(y=mx+b\) sustituyendo en\(m\) y\(b\).
Algebraico
Para los ejercicios 6-11, determine si las líneas dadas por las ecuaciones siguientes son paralelas, perpendiculares, o ni paralelas ni perpendiculares:
6)\(4x−7y=10 \\ 7x+4y=1\)
7)\(3y+x=12 \\ −y=8x+1\)
- Contestar
-
ni paralelo ni perpendicular
8)\(3y+4x=12 \\ −6y=8x+1\)
9)\(6x−9y=10 \\ 3x+2y=1\)
- Contestar
-
perpendicular
10)\(y=\dfrac{2}{3}x+1 \\ 3x+2y=1\)
11)\(y=\dfrac{3}{4}x+1 \\ −3x+4y=1\)
- Contestar
-
paralelo
Para los ejercicios 12-17, encuentra las\(x\) - y\(y\) -intercepciones de cada ecuación
12)\(f(x)=−x+2\)
13)\(g(x)=2x+4\)
- Contestar
-
\((–2, 0); (0, 4)\)
14)\(h(x)=3x−5\)
15)\(k(x)=−5x+1\)
- Contestar
-
\(\left(\dfrac{1}{5}, 0\right); (0, 1)\)
16)\(−2x+5y=20\)
17)\(7x+2y=56\)
- Contestar
-
\((8, 0); (0, 28)\)
Para los ejercicios 18-23, usa las descripciones de cada par de líneas que se indican a continuación para encontrar las pendientes de la Línea 1 y la Línea 2. ¿Cada par de líneas es paralela, perpendicular o ninguna?
18)
Línea 1: Pasa a través\((0,6)\) y\((3,−24)\)
Línea 2: Pasa a través\((−1,19)\) y\((8,−71)\)
19)
Línea 1: Pasa a través\((−8,−55)\) y\((10, 89)\)
Línea 2: Pasa a través\((9,−44)\) y\((4,−14)\)
- Contestar
-
Línea 1:\(m=8\) Línea 2:\(m=–6\) Ninguna
20)
Línea 1: Pasa a través\((2,3)\) y (4, −1)
Línea 2: Pasa a través\((6,3)\) y\((8,5)\)
21)
Línea 1: Pasa a través\((1,7)\) y\((5,5)\)
Línea 2: Pasa a través\((−1,−3)\) y\((1,1)\)
- Contestar
-
Línea 1:\(m=–12\) Línea 2:\(m=2\) Perpendicular
22)
Línea 1: Pasa a través\((0,5)\) y\((3,3)\)
Línea 2: Pasa a través\((1,−5)\) y\((3,−2)\)
23)
Línea 1: Pasa a través\((2,5)\) y\((5,−1)\)
Línea 2: Pasa a través\((−3,7)\) y\((3,−5)\)
- Contestar
-
Línea 1:\(m=–2\) Línea 2:\(m=–2\) Paralelo
24) Escribir una ecuación para una línea paralela\(f(x)=−5x−3\) y que pasa por el punto\((2, –12)\).
25) Escribir una ecuación para una línea paralela\(g(x)=3x−1\) y que pasa por el punto\((4,9)\).
- Contestar
-
\(g(x)=3x−3\)
26) Escribir una ecuación para una línea perpendicular al punto\(h(t)=−2t+4\) y que pasa por él\((-4, –1)\).
27) Escribir una ecuación para una línea perpendicular al punto\(p(t)=3t+4\) y que pasa por él\((3,1)\).
- Contestar
-
\(p(t)=−\dfrac{1}{3}t+2\)
28) Encuentra el punto en el que la línea\(f(x)=−2x−1\) se cruza con la línea\(g(x)=−x\).
29) Encuentra el punto en el que la línea\(f(x)=2x+5\) se cruza con la línea\(g(x)=−3x−5\).
- Contestar
-
\((−2,1)\)
30) Use álgebra para encontrar el punto en el que la línea\(f(x)= −\dfrac{4}{5}x +\dfrac{274}{25}\) se cruza con la línea\(h(x)=\dfrac{9}{4}x + \dfrac{73}{10}\).
31) Use álgebra para encontrar el punto en el que la línea\(f(x)=\dfrac{7}{4}x + \dfrac{457}{60}\) se cruza con la línea\(g(x)=\dfrac{4}{3}x + \dfrac{31}{5}\).
- Contestar
-
\(\left(−\dfrac{17}{5},\dfrac{5}{3}\right)\)
Gráfica
Para los ejercicios 32-37, empareja la ecuación lineal dada con su gráfica en la Figura siguiente.
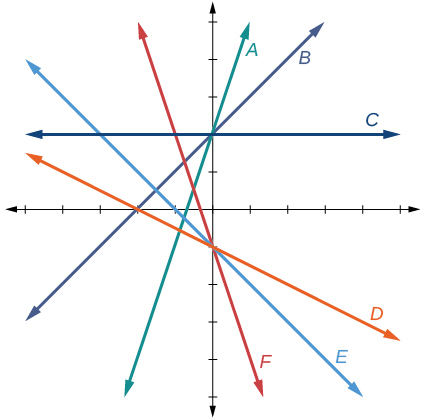
32)\(f(x)=−x−1\)
33)\(f(x)=−2x−1\)
- Contestar
-
F
34)\(f(x)=−\dfrac{1}{2}x−1\)
35)\(f(x)=2\)
- Contestar
-
C
36)\(f(x)=2+x\)
37)\(f(x)=3x+2\)
- Contestar
-
A
Para los ejercicios 38-43, esboza una línea con las características dadas.
38) Una\(x\) intercepción\((–4, 0)\) e\(y\) intercepción de\((0, –2)\)
39) Una\(x\) intercepción\((–2, 0)\) e\(y\) intercepción de\((0, 4)\)
- Contestar
-
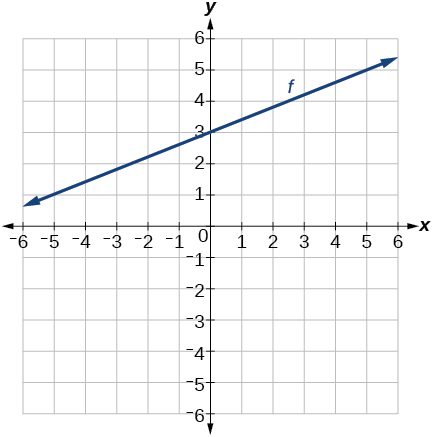
40) A\(y\) -intercepción\((0, 7)\) y pendiente\(−\dfrac{3}{2}\)
41) A\(y\) -intercepción\((0, 3)\) y pendiente\(\dfrac{2}{5}\)
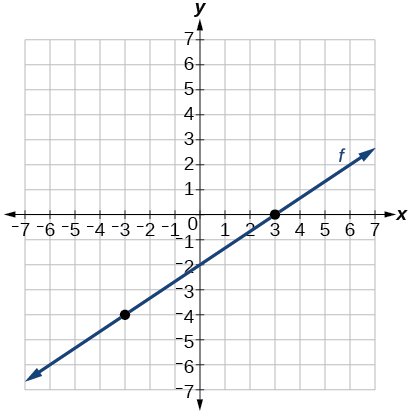
- Contestar
-
42) Pasando por los puntos\((–6, –2)\) y\((6, –6)\)
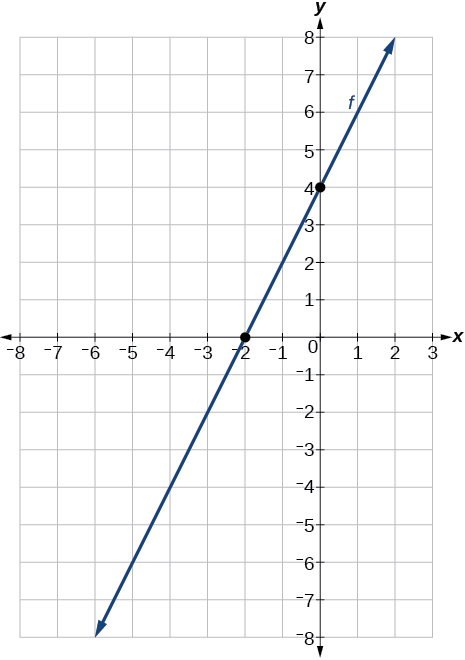
43) Pasando por los puntos\((–3, –4)\) y\((3, 0)\)
- Contestar
-
Para los ejercicios 44-58, esbozar la gráfica de cada ecuación.
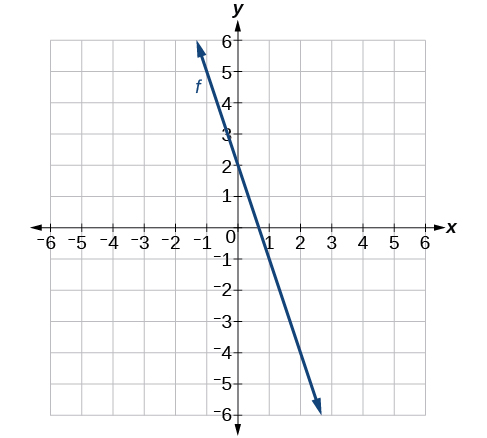
44)\(f(x)=−2x−1\)
45)\(g(x)=−3x+2\)
- Contestar
-
46)\(h(x)=\dfrac{1}{3}x+2\)
47)\(k(x)=\dfrac{2}{3}x−3\)
- Contestar
-
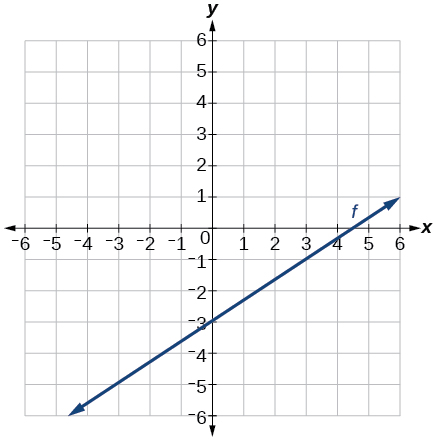
48)\(f(t)=3+2t\)
49)\(p(t)=−2 + 3t\)
- Contestar
-
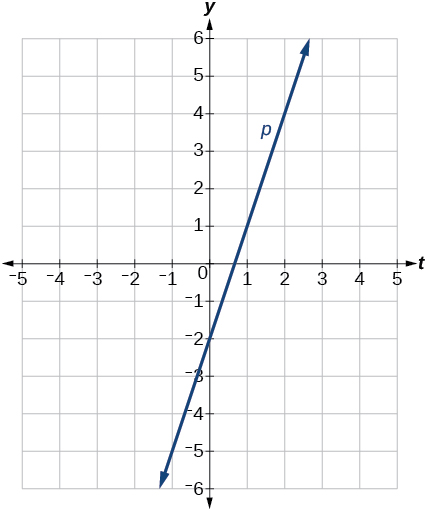
50)\(x=3\)
51)\(x=−2\)
- Contestar
-
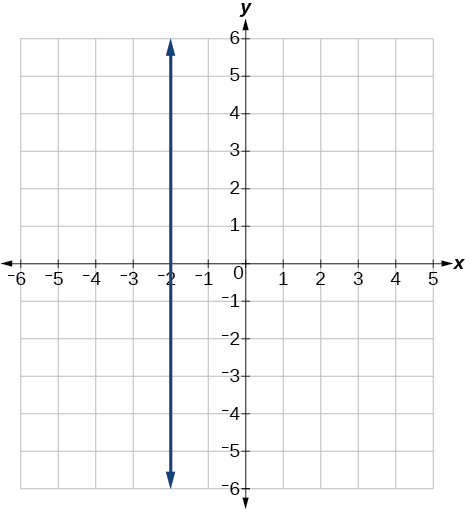
52)\(r(x)=4\)
53)\(q(x)=3\)
- Contestar
-
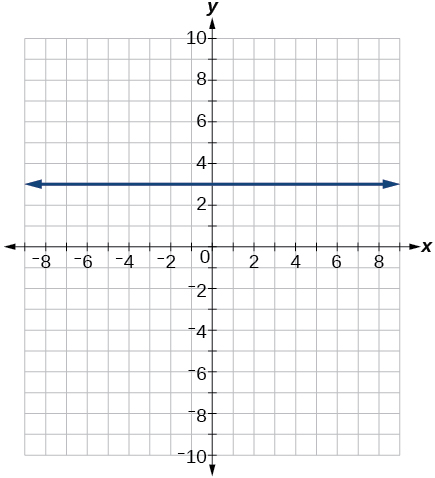
54)\(4x=−9y+36\)
55)\(\dfrac{x}{3}−\dfrac{y}{4}=1\)
- Contestar
-
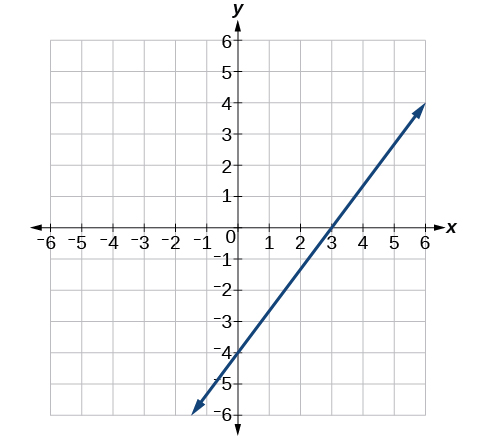
56)\(3x−5y=15\)
57)\(3x=15\)
- Contestar
-
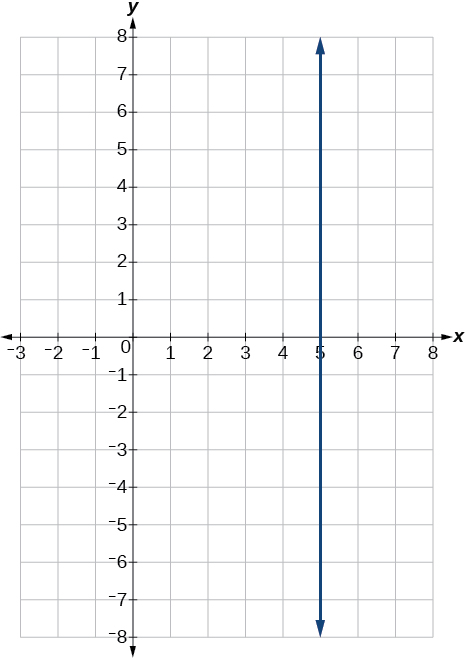
58)\(3y=12\)
59) Si\(g(x)\) es la transformación de\(f(x)=x\) después de una compresión vertical por\(\dfrac{3}{4}\), un desplazamiento a la derecha por\(2\), y un desplazamiento hacia abajo por\(4\)
- Escribe una ecuación para\(g(x)\).
- ¿Cuál es la pendiente de esta línea?
- Encuentra la\(y\) -intercepción de esta línea.
- Contestar
-
- \(g(x)=0.75x−5.5\)
- \(0.75\)
- \(0,-5.5)\)
60) Si\(g(x)\) es la transformación de\(f(x)=x\) después de una compresión vertical por\(\dfrac{1}{3}\), un desplazamiento dejado por\(1\), y un cambio hacia arriba por\(3\)
- Escribe una ecuación para\(g(x)\).
- ¿Cuál es la pendiente de esta línea?
- Encuentra la\(y\) -intercepción de esta línea.
Para los ejercicios 61-64, escriba la ecuación de la línea que se muestra en la gráfica.
61)
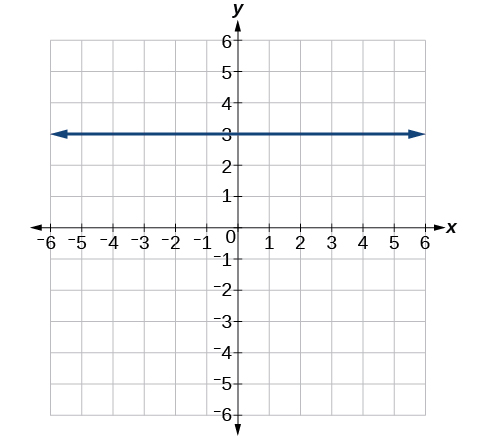
- Contestar
-
\(y=3\)
62)
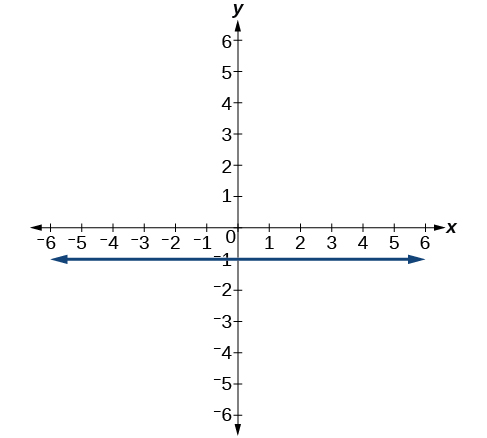
63)
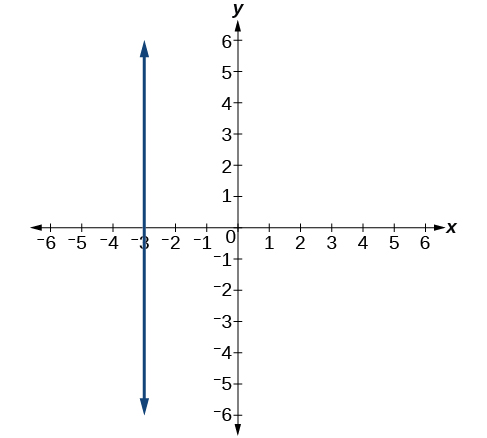
- Contestar
-
\(x=−3\)
64)
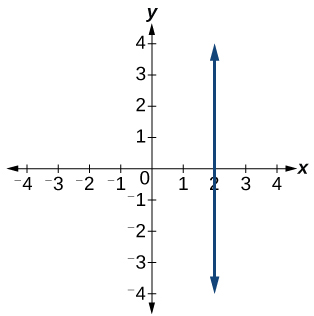
Para los ejercicios 65-69, encuentra el punto de intersección de cada par de líneas si existe. Si no existe, indicar que no hay punto de intersección.
65)\(y=\dfrac{3}{4}x+1 \\ −3x+4y=12\)
- Contestar
-
sin punto de intersección
66)\(2x−3y=12 \\ 5y+x=30\)
67)\(2x=y−3 \\ y+4x=15\)
- Contestar
-
\((2, 7)\)
68)\(x−2y+2=3 \\ x−y=3 \)
69)\(5x+3y=−65 \\ x−y=−5 \)
- Contestar
-
\((–10, –5)\)
Extensiones
70) Encuentra la ecuación de la línea paralela a la línea\(g(x)=−0.01x + 2.01\) a través del punto\((1, 2)\).
71) Encuentra la ecuación de la línea perpendicular a la línea\(g(x)=−0.01x+2.01\) a través del punto\((1, 2)\).
- Contestar
-
\(y=100x−98\)
Para los ejercicios 72-73, utilice las funciones\(f(x)=−0.1x+200\) y\(g(x)=20x+0.1\).
72) Encontrar el punto de intersección de las líneas\(f\) y\(g\).
73) Donde es\(f(x)\) mayor que\(g(x)?\) Donde es\(g(x)\) mayor que\(f(x)?\)
- Contestar
-
\(x<\dfrac{1999}{201}x>\dfrac{1999}{201}\)
Aplicaciones del mundo real
74) Una empresa de renta de autos ofrece dos planes para rentar un auto.
Plan A:\(\$30\) por día y\(\$0.18\) por milla
Plan B:\(\$50\) por día con kilometraje ilimitado gratuito
¿Cuántas millas necesitarías conducir para el plan B para ahorrarte dinero?
75) Una compañía de telefonía celular ofrece dos planes por minutos.
Plan A:\(\$20\) por mes y\(\$1\) por cada cien textos.
Plan B:\(\$50\) por mes con textos gratuitos ilimitados.
¿Cuántos textos necesitarías enviar por mes para el plan B para ahorrarte dinero?
- Contestar
-
Menos que\(3000\) textos
76) Una compañía de telefonía celular ofrece dos planes por minutos.
Plan A:\(\$15\) por mes y\(\$2\) por cada\(300\) texto.
Plan B:\(\$25\) por mes y\(\$0.50\) por cada\(100\) texto.
¿Cuántos textos necesitarías enviar por mes para el plan B para ahorrarte dinero?
2.3 Modelado con Funciones Lineales
Verbal
1) Explicar cómo encontrar la variable de entrada en un problema de palabras que utiliza una función lineal.
- Contestar
-
Determinar la variable independiente. Esta es la variable de la que depende la salida.
2) Explicar cómo encontrar la variable de salida en un problema de palabras que utiliza una función lineal.
3) Explicar cómo interpretar el valor inicial en un problema de palabras que utiliza una función lineal.
- Contestar
-
Para determinar el valor inicial, busque la salida cuando la entrada sea igual a cero.
4) Explicar cómo determinar la pendiente en un problema de palabras que utiliza una función lineal.
Algebraico
5) Encuentra el área de un paralelogramo delimitada por el\(y\) eje, la línea\(x=3\), la línea\(f(x)=1+2x\) y la línea paralela al\(f(x)\) paso (2, 7).
- Contestar
-
\(6\)unidades cuadradas
6) Encontrar el área de un triángulo delimitada por el\(x\) eje -eje, la línea\(f(x)=12–\dfrac{1}{3}x\), y la línea perpendicular a la\(f(x)\) que pasa por el origen.
7) Encontrar el área de un triángulo delimitada por el\(y\) eje -eje, la línea\(f(x)=9–\dfrac{6}{7}x\), y la línea perpendicular a la\(f(x)\) que pasa por el origen.
- Contestar
-
\(20.012\)unidades cuadradas
8) Encuentra el área de un paralelogramo delimitada por el\(x\) eje -eje\(g(x)=2\), la línea\(f(x)=3x\), la línea y la línea paralela al\(f(x)\) paso (6,1).
Para los ejercicios 9-10, considere este escenario: La población de un pueblo ha ido disminuyendo a un ritmo constante. En 2010 la población era\(5,900\). Para 2012 la población había bajado\(4,700\). Supongamos que esta tendencia continúa.
9) Predecir la población en 2016.
- Contestar
-
\(2,300\)
10) Identificar el año en que llegará la población\(0\).
Para los ejercicios 11-12, considere este escenario: La población de un pueblo se ha incrementado a un ritmo constante. En 2010 la población era\(46,020\). Para 2012 la población había aumentado a\(52,070\). Supongamos que esta tendencia continúa.
11) Predecir la población en 2016.
- Contestar
-
\(64,170\)
12) Identificar el año en que llegará la población\(75,000\).
Para los ejercicios 13-18, considera este escenario: Un pueblo tiene una población inicial de\(75,000\). Crece a una tasa constante de\(2,500\) por año durante\(5\) años.
13) Encontrar la función lineal que modela la población\(P\) del pueblo en función del año\(t\), donde\(t\) está el número de años desde que comenzó el modelo.
- Contestar
-
\(P(t)=75,000+2500t\)
14) Encontrar un dominio y rango razonables para la función\(P\).
15) Si\(P\) se grafica la función, encuentra e interpreta las\(y\) intercepciones\(x\) - y -intersecciones.
- Contestar
-
\((-30, 0)\)Treinta años antes del inicio de este modelo, el pueblo no tenía. \((0, 75,000)\)Inicialmente, el pueblo contaba con una población de\(75,000\).
16) Si\(P\) se grafica la función, encuentra e interpreta la pendiente de la función.
17) ¿Cuándo alcanzará la salida\(100,000\)?
- Contestar
-
Diez años después de que comenzara el modelo.
18) ¿Cuál es la producción en el año\(12\) años desde el inicio del modelo?
Para los ejercicios 19-24, considera este escenario: El peso de un recién nacido es de\(7.5\) libras. El bebé ganaba media libra al mes por su primer año.
19) Encontrar la función lineal que modela el peso\(W\) del bebé en función de la edad del bebé, en meses,\(t\).
- Contestar
-
\(W(t)=7.5t+0.5\)
20) Encontrar un dominio y rango razonables para la función\(W\).
21) Si\(W\) se grafica la función, encuentra e interpreta las\(y\) intercepciones\(x\) - y -intersecciones.
- Contestar
-
\((−15,0)\): El\(x\) -intercepto no es un conjunto plausible de datos para este modelo porque significa que el bebé pesaba\(0\) libras\(15\) meses antes del nacimiento. \((0, 7.5)\): El bebé pesaba\(7.5\) libras al nacer.
22) Si\(W\) se grafica la función, encuentra e interpreta la pendiente de la función.
23) ¿Cuándo pesó el bebé\(10.4\) libras?
- Contestar
-
A los\(5.8\) meses de edad.
24) ¿Cuál es la salida cuando la entrada es\(6.2\)? Interpreta tu respuesta.
Para los ejercicios 25-30, considere este escenario: El número de personas afligidas por el resfriado común en los meses de invierno disminuyó de manera constante\(205\) cada año desde 2005 hasta 2010. En 2005, la\(12,025\) gente estaba afligida.
25) Encontrar la función lineal que modela el número de personas infligidas con el resfriado\(C\) común en función del año,\(t\).
- Contestar
-
\(C(t)=12,025−205t\)
26) Encontrar un dominio y rango razonables para la función\(C\).
27) Si\(C\) se grafica la función, encuentra e interpreta las\(y\) intercepciones\(x\) - y -intersecciones.
- Contestar
-
\((58.7, 0)\): En aproximadamente\(59\) años, el número de personas infligidas con el resfriado común sería\(0\). \((0,12,025)\): Inicialmente había\(12,025\) gente afligida por el resfriado común.
28) Si\(C\) se grafica la función, encuentra e interpreta la pendiente de la función.
29) ¿Cuándo alcanzará la salida\(0\)?
- Contestar
-
\(2064\)
30) ¿En qué año será el número de personas\(9,700\)?
Gráfica
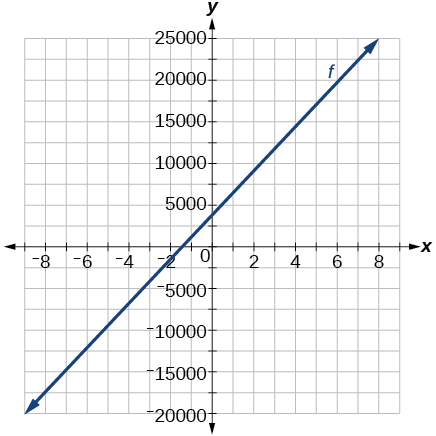
Para los ejercicios 31-34, utilice la gráfica de la siguiente Figura, que muestra el beneficio\(y\), en miles de dólares, de una empresa en un año determinado,\(t\), donde\(t\) representa el número de años desde 1980.
.jpg)
31) Encontrar la función lineal\(y\), donde\(y\) depende\(t\), el número de años desde 1980.
- Contestar
-
\(y=−2t+180\)
32) Encontrar e interpretar la\(y\) -intercepción.
33) Encontrar e interpretar la\(x\) -intercepción.
- Contestar
-
En 2070, la ganancia de la compañía será cero.
34) Encontrar e interpretar la pendiente.
Para los ejercicios 35-38, utilice la gráfica de la siguiente Figura, que muestra el beneficio\(y\), en miles de dólares, de una empresa en un año determinado,\(t\), donde\(t\) representa el número de años desde 1980.
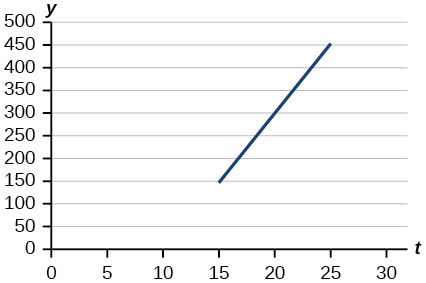
35) Encontrar la función lineal\(y\), donde\(y\) depende\(t\), el número de años desde 1980.
- Contestar
-
\(y=30t−300\)
36) Encontrar e interpretar la\(y\) -intercepción.
37) Encontrar e interpretar la\(x\) -intercepción.
- Contestar
-
\((10, 0)\)En 1990, el beneficio obtuvo ganancia cero.
38) Encontrar e interpretar la pendiente.
Numérico
Para los ejercicios 39-41, use los valores promedio de los hogares en Mississippi y Hawái (ajustados por inflación) que se muestran en la Tabla siguiente. Supongamos que los valores de la casa están cambiando linealmente.
| Año | Mississippi | Hawaii |
|---|---|---|
| 1950 | 25,200 | $74,400 |
| 2000 | 71,400 | $272,700 |
39) ¿En qué estado han aumentado los valores de las viviendas a un ritmo mayor?
- Contestar
-
Hawaii
40) Si estas tendencias continuaran, ¿cuál sería el valor medio de la vivienda en Mississippi en 2010?
41) Si asumimos que la tendencia lineal existió antes de 1950 y continúa después del 2000, ¿los valores medios de la casa de los dos estados serán (o fueron) iguales en qué año? (La respuesta puede ser absurda.)
- Contestar
-
Durante el año 1933
Para los ejercicios 42-44, use los valores promedio de los hogares en Indiana y Alabama (ajustados por inflación) que se muestran en la Tabla siguiente. Supongamos que los valores de la casa están cambiando linealmente.
| Año | Indiana | Alabama |
|---|---|---|
| 1950 | 37,700 | $27,100 |
| 2000 | $94,300 | $85,100 |
42) ¿En qué estado han aumentado los valores de las viviendas a un ritmo mayor?
43) Si estas tendencias continuaran, ¿cuál sería la mediana del valor de la vivienda en Indiana en 2010?
- Contestar
-
\(\$105,620\)
44) Si asumimos que la tendencia lineal existió antes de 1950 y continúa después del 2000, ¿los valores medios de la casa de los dos estados serán (o fueron) iguales en qué año? (La respuesta puede ser absurda.)
Aplicaciones del mundo real
45) En 2004, se encontraba una población escolar\(1001\). Para 2008 la población había crecido hasta\(1697\). Supongamos que la población está cambiando linealmente.
- ¿Cuánto creció la población entre el año 2004 y 2008?
- ¿Cuánto tiempo tardó la población en crecer de\(1001\) estudiantes a\(1697\) estudiantes?
- ¿Cuál es el crecimiento promedio de la población por año?
- ¿Cuál era la población en el año 2000?
- Encontrar una ecuación para la población,\(P\), de los\(t\) años escolares posteriores al 2000.
- Usando tu ecuación, predice la población de la escuela en 2011.
- Contestar
-
- \(696\)personas
- \(4\)años
- \(174\)personas por año
- \(305\)personas
- \(P(t)=305+174t\)
- \(2219\)personas
46) En 2003, la población de un pueblo era\(1431\). Para 2007 la población había crecido hasta\(2134\). Supongamos que la población está cambiando linealmente.
- ¿Cuánto creció la población entre el año 2003 y 2007?
- ¿Cuánto tiempo tardó la población en crecer de\(1431\) personas a\(2134\) personas?
- ¿Cuál es el crecimiento promedio de la población por año?
- ¿Cuál era la población en el año 2000?
- Encontrar una ecuación para la población,\(P\) del pueblo\(t\) años después del 2000.
- Usando tu ecuación, predice la población del pueblo en 2014.
47) Una compañía telefónica tiene un plan celular mensual donde un cliente paga una cuota mensual fija y luego una cierta cantidad de dinero por minuto utilizada en el teléfono. Si un cliente usa\(410\) minutos, el costo mensual será\(\$71.50\). Si el cliente utiliza\(720\) minutos, el costo mensual será\(\$118\).
- Interpretar la pendiente y\(y\) -intercepción de la ecuación.
- Usa tu ecuación para encontrar el costo mensual total si se utilizan los\(687\) minutos.
- Contestar
-
- \(C(x)=0.15x+10\)
- La tarifa mensual plana es\(\$10\) y hay una\(\$0.15\) tarifa adicional por cada minuto adicional utilizado
- \(\$113.05\)
48) Una compañía telefónica tiene un plan mensual de datos celulares donde un cliente paga una cuota mensual fija de\(\$10\) y luego una cierta cantidad de dinero por megabyte (MB) de datos utilizados en el teléfono. Si un cliente usa\(20\) MB, el costo mensual será\(\$11.20\). Si el cliente utiliza\(130\) MB, el costo mensual será\(\$17.80\).
- Interpretar la pendiente y\(y\) -intercepción de la ecuación.
- Usa tu ecuación para encontrar el costo mensual total si se utilizan\(250\) MB.
49) En 1991, la población de alces en un parque se midió para ser\(4,360\). Para 1999, la población se midió nuevamente para ser\(5,880\). Supongamos que la población sigue cambiando linealmente.
- ¿Qué predice tu modelo que será la población de alces en 2003?
- Contestar
-
- \(P(t)=190t+4360\)
- \(6640\)alce
50) En 2003, la población de búhos en un parque se midió para ser\(340\). Para 2007, la población se volvió a medir para ser\(285\). La población cambia linealmente. Que el insumo sean años desde 1990.
- ¿Qué predice tu modelo que será la población de búhos en 2012?
51) La Reserva Federal de Helio tenía alrededor de\(16\) mil millones de pies cúbicos de helio en 2010 y se está agotando en alrededor de\(2.1\) mil millones de pies cúbicos cada año.
- En 2015, ¿cuáles serán las reservas de helio?
- Si la tasa de agotamiento no cambia, ¿en qué año se agotará la Reserva Federal de Helio?
- Responder
-
- \(R(t)=16−2.1t\)
- \(5.5\)mil millones de pies cúbicos
- Durante el año 2017
52) Supongamos que las reservas mundiales de petróleo en 2014 son\(1,820\) mil millones de barriles. Si, en promedio, las reservas totales están disminuyendo en\(25\) mil millones de barriles de petróleo cada año:
- Dentro de siete años, ¿cuáles serán las reservas petroleras?
- Si la tasa a la que disminuyen las reservas es constante, ¿cuándo se agotarán las reservas mundiales de petróleo?
53) Estás eligiendo entre dos planes diferentes de telefonía celular prepago. El primer plan cobra una tasa de\(26\) centavos por minuto. El segundo plan cobra una cuota mensual de\(\$19.95\) más\(11\) centavos por minuto. ¿Cuántos minutos tendrías que usar en un mes para que el segundo plan sea preferible?
- Responder
-
Más de\(133\) minutos
54) Está eligiendo entre dos empresas de lavado de ventanas diferentes. Los primeros cargos\(\$5\) por ventana. El segundo cobra una tarifa base de\(\$40\) más\(\$3\) por ventana. ¿Cuántas ventanas necesitarías tener para que la segunda compañía sea preferible?
55) Cuando se contrata en un nuevo trabajo vendiendo joyas, se le dan dos opciones de pago:
Opción A: Sueldo base de\(\$17,000\) un año con una comisión\(12\%\) de tus ventas
Opción B: Sueldo base de\(\$20,000\) un año con una comisión\(5\%\) de tus ventas
¿Cuántas joyas necesitarías vender para la opción A para producir un ingreso mayor?
- Responder
-
Más que\(\$42,857.14\) valor de joyas
56) Cuando se contrata en un nuevo trabajo vendiendo electrónica, se le dan dos opciones de pago:
Opción A: Sueldo base de\(\$14,000\) un año con una comisión\(10\%\) de tus ventas
Opción B: Sueldo base de\(\$19,000\) un año con una comisión\(4\%\) de tus ventas
¿Cuánta electrónica necesitaría vender para la opción A para producir un ingreso mayor?
57) Cuando se contrata en un nuevo trabajo vendiendo electrónica, se le dan dos opciones de pago:
Opción A: Sueldo base de\(\$20,000\) un año con una comisión\(12\%\) de tus ventas
Opción B: Sueldo base de\(\$26,000\) un año con una comisión\(3\%\) de tus ventas
¿Cuánta electrónica necesitaría vender para la opción A para producir un ingreso mayor?
- Responder
-
\(\$66,666.67\)
58) Cuando se contrata en un nuevo trabajo vendiendo electrónica, se le dan dos opciones de pago:
Opción A: Sueldo base de\(\$10,000\) un año con una comisión\(9\%\) de tus ventas
Opción B: Sueldo base de\(\$20,000\) un año con una comisión\(4\%\) de tus ventas
¿Cuánta electrónica necesitaría vender para la opción A para producir un ingreso mayor?
2.4 Montaje de modelos lineales a datos
Verbal
1) Describir lo que significa si hay un desglose del modelo al usar un modelo lineal.
- Responder
-
Cuando nuestro modelo ya no se aplica, después de algún valor en el dominio, el modelo en sí no se sostiene.
2) ¿Qué es la interpolación cuando se utiliza un modelo lineal?
3) ¿Qué es la extrapolación cuando se utiliza un modelo lineal?
- Responder
-
Predecimos un valor fuera del dominio y rango de los datos.
4) Explicar la diferencia entre un coeficiente de correlación positivo y uno negativo.
5) Explicar cómo interpretar el valor absoluto de un coeficiente de correlación.
- Responder
-
Cuanto más cerca esté el número\(1\), menos dispersos serán los datos, cuanto más cerca esté el número\(0\), más dispersos serán los datos.
Algebraico
6) Se realizó una regresión para determinar si existe una relación entre las horas de televisión que se ven al día (x) y el número de sentadillas que una persona puede hacer (y). A continuación se dan los resultados de la regresión. Use esto para predecir la cantidad de abdominales que puede hacer una persona que ve\(11\) horas de televisión.
\[\begin{array}{l}{y=a x+b} \\ {a=-1.341} \\ {b=32.234} \\ {r=-0.896}\end{array}\nonumber\]
7) Se realizó una regresión para determinar si existe una relación entre el diámetro de un árbol (\(x\), en pulgadas) y la edad del árbol (\(y\), en años). A continuación se dan los resultados de la regresión. Use esto para predecir la edad de un árbol con\(10\) pulgadas de diámetro. \[\begin{array}{l}{y=a x+b} \\ {a=6.301} \\ {b=-1.044} \\ {r=-0.970}\end{array}\nonumber\]
- Responder
-
\(61.966\)años
Para los ejercicios 8-11, dibuje un diagrama de dispersión para los datos proporcionados. ¿Los datos parecen estar relacionados linealmente?
8)
| 0 | 2 | 4 | 6 | 8 | 10 |
| —22 | —19 | —15 | —11 | —6 | —2 |
9)
| 1 | 2 | 3 | 4 | 5 | 6 |
| 46 | 50 | 59 | 75 | 100 | 136 |
- Responder
-
No
10)
| 100 | 250 | 300 | 450 | 600 | 750 |
| 12 | 12.6 | 13.1 | 14 | 14.5 | 15.2 |
11)
| 1 | 3 | 5 | 7 | 9 | 11 |
| 1 | 9 | 28 | 65 | 125 | 216 |
- Responder
-
No
12) Para los siguientes datos, dibuje un diagrama de dispersión. Si quisiéramos saber cuándo llegaría la población\(15,000\), ¿la respuesta implicaría interpolación o extrapolación? Eyeball la línea, y estimar la respuesta.
| Año | Población |
|---|---|
| 1990 | 11,500 |
| 1995 | 12,100 |
| 2000 | 12,700 |
| 2005 | 13,000 |
| 2010 | 13,750 |
13) Para los siguientes datos, dibuje un diagrama de dispersión. Si quisiéramos saber cuándo alcanzaría la temperatura\(28^{\circ} F\), ¿la respuesta implicaría interpolación o extrapolación? Eyeball la línea y estimar la respuesta.
| Temperatura, °F | 16 | 18 | 20 | 25 | 30 |
| Tiempo, segundos | 46 | 50 | 54 | 55 | 62 |
- Responder
-
Interpolación. Acerca de\(60° F\).
Gráfica
Para los ejercicios 14-17, haga coincidir cada diagrama de dispersión con una de las cuatro correlaciones especificadas en la Figura ab y la Figura cd.
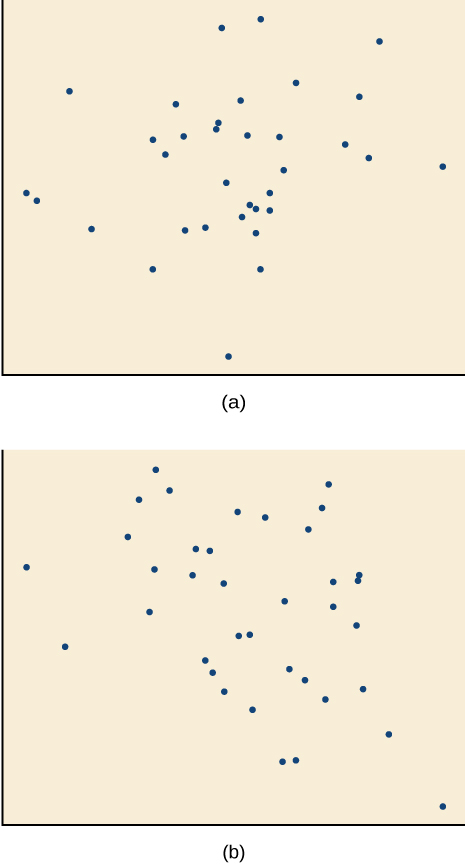
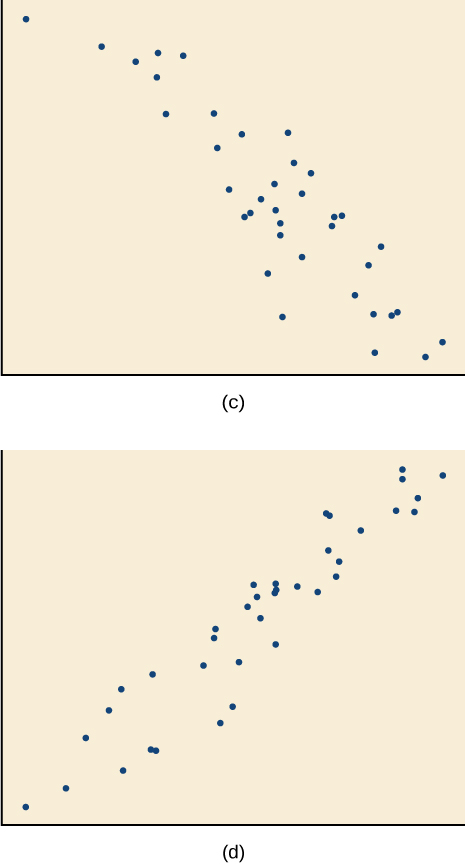
14)\(r=0.95\)
15)\(r=−0.89\)
- Responder
-
C
16)\(r=0.26\)
17)\(r=−0.39\)
- Responder
-
B
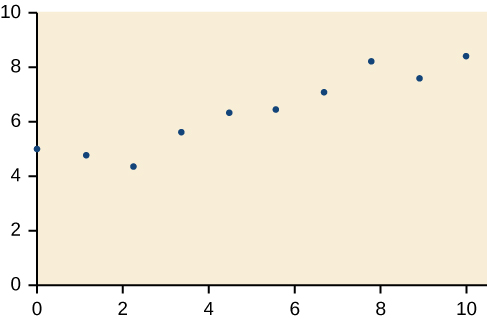
Para los ejercicios 18-21, dibuje una línea de mejor ajuste para los datos trazados.
18)
19)
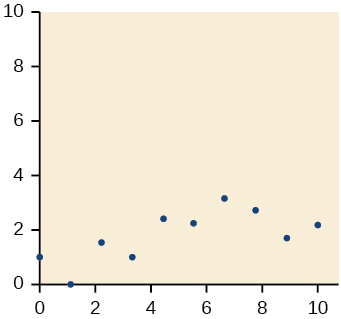
- Responder
-
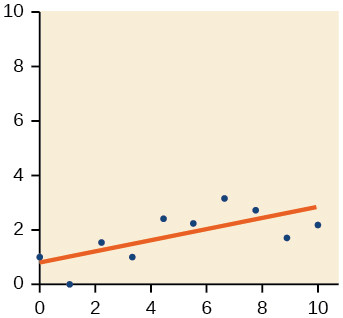
20)
21)
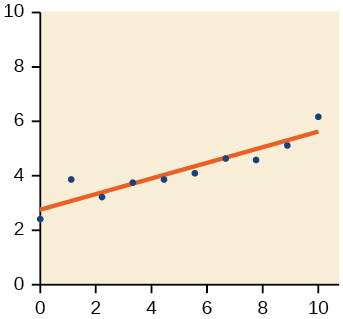
- Responder
-
Numérico
22) El Censo de Estados Unidos rastrea el porcentaje de personas de\(25\) años o más que son egresados universitarios. Esos datos de varios años se dan en la Tabla siguiente. Determinar si la tendencia aparece lineal. Si es así, y suponiendo que la tendencia continúe, ¿en qué año superará el porcentaje\(35\%\)?
| Año | Porcentaje de egresados |
|---|---|
| 1990 | 21.3 |
| 1992 | 21.4 |
| 1994 | 22.2 |
| 1996 | 23.6 |
| 1998 | 24.4 |
| 2000 | 25.6 |
| 2002 | 26.7 |
| 2004 | 27.7 |
| 2006 | 28 |
| 2008 | 29.4 |
23) La importación estadounidense de vino (en hectolitros) por varios años se da en la Tabla. Determinar si la tendencia aparece lineal. Si es así, y suponiendo que la tendencia continúe, ¿en qué año las importaciones superarán los\(12,000\) hectolitros?
| Año | Importaciones |
|---|---|
| 1992 | 2665 |
| 1994 | 2688 |
| 1996 | 3565 |
| 1998 | 4129 |
| 2000 | 4584 |
| 2002 | 5655 |
| 2004 | 6549 |
| 2006 | 7950 |
| 2008 | 8487 |
| 2009 | 9462 |
- Responder
-
Sí, la tendencia aparece lineal porque\(r=0.985\) y superará\(12,000\) cerca de mediados de año, 2016,\(24.6\) años desde 1992.
24) El Cuadro muestra el año y el número de personas desempleadas en una ciudad en particular desde hace varios años. Determinar si la tendencia aparece lineal. Si es así, y suponiendo que la tendencia continúe, ¿en qué año llegará el número de desempleados\(5\)?
| Año | Número Desempleados |
|---|---|
| 1990 | 750 |
| 1992 | 670 |
| 1994 | 650 |
| 1996 | 605 |
| 1998 | 550 |
| 2000 | 510 |
| 2002 | 460 |
| 2004 | 420 |
| 2006 | 380 |
| 2008 | 320 |
Tecnología
Para los ejercicios 25-31, utilice cada conjunto de datos para calcular la línea de regresión utilizando una calculadora u otra herramienta tecnológica, y determinar el coeficiente de correlación con los\(3\) decimales de precisión.
25)
| \(x\) | 8 | 15 | 26 | 31 | 56 |
|---|---|---|---|---|---|
| \(y\) | 23 | 41 | 53 | 72 | 103 |
- Responder
-
\(y=1.640x+13.800, r=0.987\)
26)
| \(x\) | 5 | 7 | 10 | 12 | 15 |
|---|---|---|---|---|---|
| \(y\) | 4 | 12 | 17 | 22 | 24 |
27)
| \(x\) | \(y\) | \(x\) | \(y\) |
|---|---|---|---|
| \ (x\) ">3 | \ (y\) ">21.9 | \ (x\) ">11 | \ (y\) ">15.76 |
| \ (x\) ">4 | \ (y\) ">22.22 | \ (x\) ">12 | \ (y\) ">13.68 |
| \ (x\) ">5 | \ (y\) ">22.74 | \ (x\) ">13 | \ (y\) ">14.1 |
| \ (x\) ">6 | \ (y\) ">22.26 | \ (x\) ">14 | \ (y\) ">14.02 |
| \ (x\) ">7 | \ (y\) ">20.78 | \ (x\) ">15 | \ (y\) ">11.94 |
| \ (x\) ">8 | \ (y\) ">17.6 | \ (x\) ">16 | \ (y\) ">12.76 |
| \ (x\) ">9 | \ (y\) ">16.52 | \ (x\) ">17 | \ (y\) ">11.28 |
| \ (x\) ">10 | \ (y\) ">18.54 | \ (x\) ">18 | \ (y\) ">9.1 |
- Responder
-
\(y=−0.962x+26.86, r=−0.965\)
28)
| \(x\) | \(y\) |
|---|---|
| \ (x\) ">4 | \ (y\) ">44.8 |
| \ (x\) ">5 | \ (y\) ">43.1 |
| \ (x\) ">6 | \ (y\) ">38.8 |
| \ (x\) ">7 | \ (y\) ">39 |
| \ (x\) ">8 | \ (y\) ">38 |
| \ (x\) ">9 | \ (y\) ">32.7 |
| \ (x\) ">10 | \ (y\) ">30.1 |
| \ (x\) ">11 | \ (y\) ">29.3 |
| \ (x\) ">12 | \ (y\) ">27 |
| \ (x\) ">13 | \ (y\) ">25.8 |
29)
| \(x\) | \(y\) |
|---|---|
| \ (x\) ">21 | \ (y\) ">17 |
| \ (x\) ">25 | \ (y\) ">11 |
| \ (x\) ">30 | \ (y\) ">2 |
| \ (x\) ">31 | \ (y\) ">−1 |
| \ (x\) ">40 | \ (y\) ">−18 |
| \ (x\) ">50 | \ (y\) ">−40 |
- Responder
-
\(y=−1.981x+60.197; r=−0.998\)
30)
| \(x\) | \(y\) |
|---|---|
| \ (x\) ">100 | \ (y\) ">2000 |
| \ (x\) ">80 | \ (y\) ">1798 |
| \ (x\) ">60 | \ (y\) ">1589 |
| \ (x\) ">55 | \ (y\) ">1580 |
| \ (x\) ">40 | \ (y\) ">1390 |
| \ (x\) ">20 | \ (y\) ">1202 |
31)
| \(x\) | \(y\) |
|---|---|
| \ (x\) ">900 | \ (y\) ">70 |
| \ (x\) ">988 | \ (y\) ">80 |
| \ (x\) ">1000 | \ (y\) ">82 |
| \ (x\) ">1010 | \ (y\) ">84 |
| \ (x\) ">1200 | \ (y\) ">105 |
| \ (x\) ">1205 | \ (y\) ">108 |
- Responder
-
\(y=0.121x−38.841, r=0.998\)
Extensiones
32) Gráfica\(f(x)=0.5x+10\). Elija un conjunto de pares\(5\) ordenados usando entradas\(x=−2, 1, 5, 6, 9\) y use regresión lineal para verificar que la función se ajuste bien a los datos.
33) Gráfica\(f(x)=−2x−10\). Elija un conjunto de pares\(5\) ordenados usando entradas\(x=−2, 1, 5, 6, 9\) y use regresión lineal para verificar la función.
- Responder
-
\((−2,−6),(1,−12),(5,−20),(6,−22),(9,−28); y=−2x−10\)
Para los ejercicios 34-36, considere este escenario: El beneficio de una empresa disminuyó de manera constante en un lapso de diez años. Los siguientes pares ordenados muestran dólares y el número de unidades vendidas en cientos y la ganancia en miles de en el lapso de diez años, (número de unidades vendidas, beneficio) para años específicos registrados:
\[(46, 1,600), (48, 1,550), (50, 1,505), (52, 1,540), (54, 1,495) \nonumber\]
34) Utilizar regresión lineal para determinar una función\(P\) donde el beneficio en miles de dólares depende del número de unidades vendidas en cientos.
35) Encuentra al décimo más cercano e interpreta la\(x\) -intercepción.
- Responder
-
\((189.8,0)\)Si se venden\(18,980\) unidades, la compañía tendrá una ganancia de cero dólares.
36) Encuentra al décimo más cercano e interpreta la\(y\) -intercepción.
Aplicaciones del mundo real
Para los ejercicios 37-38, considere este escenario: La población de una ciudad aumentó de manera constante en un lapso de diez años. Los siguientes pares ordenados muestran la población y el año en el lapso de diez años, (población, año) para años específicos registrados:
\[(2500, 2000), (2650, 2001), (3000, 2003), (3500, 2006), (4200, 2010) \nonumber \]
37) Utilizar regresión lineal para determinar una función\(y\), donde el año depende de la población. Redondear a tres decimales de precisión.
- Responder
-
\(y=0.00587x+1985.41\)
38) Predecir cuándo golpeará la población\(8,000\).
Para los ejercicios 39-40, considere este escenario: El beneficio de una empresa aumentó de manera constante en un lapso de diez años. Los siguientes pares ordenados muestran el número de unidades vendidas en cientos y el beneficio en miles de a lo largo del lapso de diez años, (número de unidades vendidas, beneficio) para años registrados específicos:
\[(46, 250), (48, 305), (50, 350), (52, 390), (54, 410) \nonumber \]
39) Utilizar regresión lineal para determinar una función\(y\), donde la ganancia en miles de dólares depende del número de unidades vendidas en cientos.
- Responder
-
\(y=20.25x−671.5\)
40) Predecir cuándo el beneficio superará el millón de dólares.
Para los ejercicios 41-42, considere este escenario: El beneficio de una empresa disminuyó de manera constante en un lapso de diez años. Los siguientes pares ordenados muestran dólares y el número de unidades vendidas en cientos y la ganancia en miles de a lo largo del lapso de diez años (número de unidades vendidas, beneficio) para años registrados específicos:
\[(46, 250), (48, 225), (50, 205), (52, 180), (54, 165) \nonumber\]
41) Utilizar regresión lineal para determinar una función\(y\), donde la ganancia en miles de dólares depende del número de unidades vendidas en cientos.
- Responder
-
\(y=−10.75x+742.50\)
42) Predecir cuándo la ganancia caerá por debajo del\(\$25,000\) umbral.


