2.R: Funciones Lineales (Revisión)
- Page ID
- 121548
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)2.1 Funciones lineales
1) Determinar si la ecuación algebraica es lineal:\(2 x+3 y=7\)
- Contestar
-
Sí
2) Determinar si la ecuación algebraica es lineal:\(6 x^{2}-y=5\)
3) Determinar si la función está aumentando o disminuyendo:\(f(x)=7 x-2\)
- Contestar
-
Incrementando
4) Determinar si la función está aumentando o disminuyendo:\(g(x)=-x+2\)
5) Dado cada conjunto de información, encontrar una ecuación lineal que satisfaga las condiciones dadas, si es posible. Pasa a través\((7,5)\) y\((3,17)\)
- Contestar
-
\(y=-3 x+26\)
6) Dado cada conjunto de información, encontrar una ecuación lineal que satisfaga las condiciones dadas, si es posible. \(x\)-interceptar\((6,0)\) e\(y\) -interceptar en\((0,10)\)
7) Encuentra la pendiente de la línea que se muestra en la gráfica de líneas.
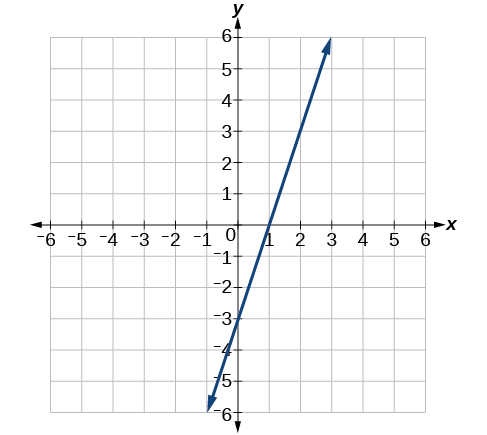
- Contestar
-
\(3\)
8) Encuentra la pendiente de la línea graficada.
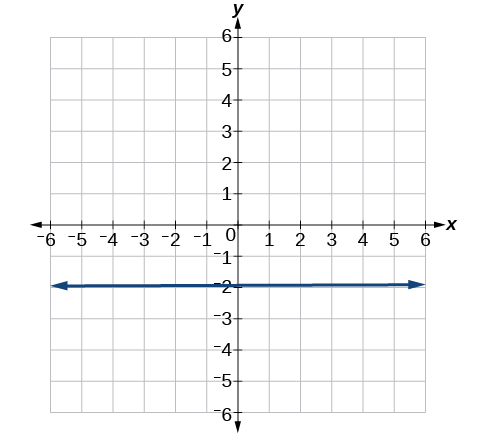
9) Escribe una ecuación en forma de pendiente-intercepción para la línea mostrada.
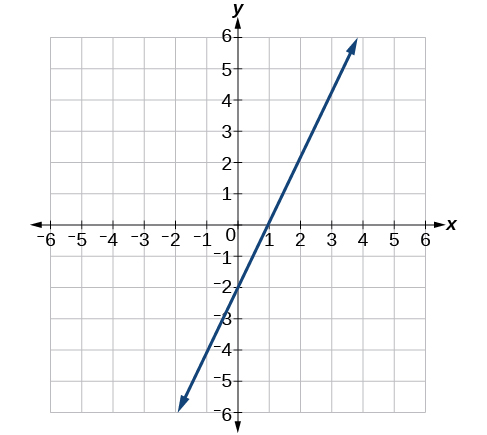
- Contestar
-
\(y=2 x-2\)
10) ¿La siguiente tabla representa una función lineal? Si es así, encuentra la ecuación lineal que modela los datos.
| \(x\) | —4 | 0 | 2 | 10 |
|---|---|---|---|---|
| \(g(x)\) | 18 | —2 | —12 | —52 |
11) ¿La siguiente tabla representa una función lineal? Si es así, encuentra la ecuación lineal que modela los datos.
| \(x\) | 6 | 8 | 12 | 26 |
|---|---|---|---|---|
| \(g(x)\) | —8 | —12 | —18 | —46 |
- Contestar
-
No lineal
12) El 1 de junio, una empresa tiene\(\$4,000,000\) ganancias. Si entonces la empresa pierde\(150,000\) dólares por día a partir de entonces en el mes de junio, ¿cuál es el beneficio de la compañía n º día después del 1 de junio?
2.2 Gráficas de Funciones Lineales
Para los ejercicios 1-2, determine si las líneas dadas por las ecuaciones siguientes son paralelas, perpendiculares, o ni paralelas ni perpendiculares:
1)\(\begin{align*} 2x-6y &=12 \\ -x+3y &=1 \end{align*} \nonumber\)
- Contestar
-
paralelo
2)\(\begin{align*} y &=\dfrac{1}{3} x-2 \\ 3x+y &=-9 \end{align*} \nonumber \)
Para los ejercicios 3-4, encuentre las intercepciones\(x\)\(y\) - y - de la ecuación dada
3)\(7 x+9 y=-63\)
- Contestar
-
\((-9,0); (0,-7)\)
4)\(f(x)=2 x-1\)
Para los ejercicios 5-11, usa las descripciones de los pares de líneas para encontrar las pendientes de la Línea 1 y la Línea 2. ¿Cada par de líneas es paralela, perpendicular o ninguna?
5)
Línea 1: Pasa a través\((5,11)\) y\((10,1)\)
la línea\(2 :\) pasa a través\((-1,3)\) y\((-5,11)\)
- Contestar
-
Línea 1:\(m=-2\); Línea 2:\(m=-2\); Paralelo
6)
Línea 1: Pasa a través\((8,-10)\) y\((0,-26)\)
Línea 2: Pasa a través\((2,5)\) y\((4,4)\)
7) Escribir una ecuación para una línea perpendicular al punto\(f(x)=5 x-1\) y que pasa por él\((5,20)\).
- Contestar
-
\(y=-0.2 x+21\)
8) Encontrar la ecuación de una línea con una\(y\) intersección de\((0,2)\) y pendiente\(-\dfrac{1}{2}\).
9) Esbozar una gráfica de la función lineal\(f(t)=2t-5\).
- Contestar
-
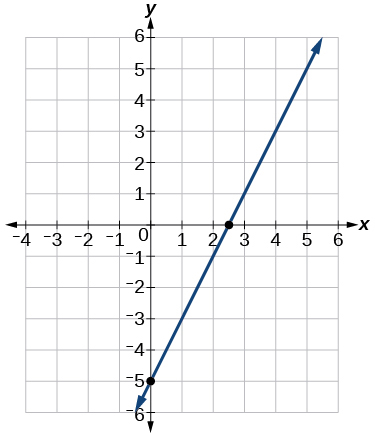
10) Encuentra el punto de intersección para las funciones\(2\) lineales:\(\begin{align*} x &=y+6 \\ 2x-y &=13 \end{align*}\)
11) Una empresa de renta de autos ofrece dos planes para rentar un auto.
Plan A:\(25\) dólares por día y\(10\) centavos por milla
Plan B:\(50\) dólares por día con kilometraje ilimitado gratuito
¿Cuántas millas necesitarías conducir para el plan B para ahorrarte dinero?
- Contestar
-
\(250\)
2.3 Modelado con Funciones Lineales
1) Encontrar el área de un triángulo delimitada por el\(y\) eje, la línea\(f(x)=10-2x\) y la línea perpendicular a la\(f\) que pasa por el origen.
2) La población de un pueblo aumenta a un ritmo constante. En 2010 la población era\(55,000\). Para 2012 la población había aumentado a\(76,000\). Si esta tendencia continúa, pronosticar la población en 2016.
- Contestar
-
\(118,000\)
3) El número de personas afectadas por el resfriado común en los meses de invierno disminuyó de manera constante\(50\) cada año desde 2004 hasta 2010. En 2004,\(875\) las personas fueron infligidas.
4) Encontrar la función lineal que modela el número de personas afligidas por el resfriado\(C\) común en función del año,\(t\). ¿Cuándo nadie será afligido?
Para los ejercicios 5-6, utilice la gráfica de la siguiente Figura que muestra el beneficio\(y\), en miles de dólares, de una empresa en un año determinado,\(x\), donde\(x\) representa años desde 1980.
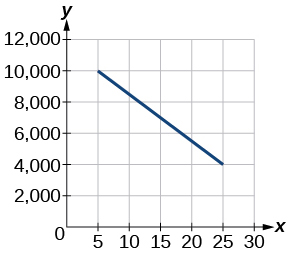
5) Encontrar la función lineal\(y\), donde\(y\) depende\(x\), el número de años desde 1980.
- Contestar
-
\(y=-300 x+11,500\)
6) Encontrar e interpretar la\(y\) -intercepción.
7) Para el siguiente ejercicio, considere este escenario: En 2004, se encontraba una población escolar\(1,700\). Para 2012 la población había crecido hasta\(2,500\). Supongamos que la población está cambiando linealmente.
- ¿Cuánto creció la población entre el año 2004 y 2012?
- ¿Cuál es el crecimiento promedio de la población por año?
- Encontrar una ecuación para la población,\(P\), de los\(t\) años escolares posteriores a 2004.
- Contestar
-
- \(800\)
- \(100\)estudiantes por año
- \(P(t)=100 t+1700\)
Para los ejercicios 8-9, considere este escenario: En el año 2000, se midió para ser la población de alces en un parque\(6,500\). Para 2010, la población se midió para ser\(12,500\). Supongamos que la población sigue cambiando linealmente.
8) Encontrar una fórmula para la población de alces,\(P\).
9) ¿Qué predice tu modelo que será la población de alces en 2020?
- Contestar
-
\(18,500\)
Para los ejercicios 10-, considere este escenario: Los valores medios de las casas en las subdivisiones Pima Central y Valle Este (ajustados por inflación) se muestran en la Tabla siguiente. Supongamos que los valores de la casa están cambiando linealmente.
| Año | Pima Central | Valle del Este |
|---|---|---|
| 1970 | 32,000 | 120,250 |
| 2010 | 85,000 | 150,000 |
10) ¿En qué subdivisión se han incrementado los valores de las casas a un ritmo mayor?
11) Si estas tendencias continuaran, ¿cuál sería el valor medio de la vivienda en Pima Central en 2015?
- Contestar
-
\(\$91,625\)
2.4 Montaje de modelos lineales a datos
1) Dibuje una gráfica de dispersión para los datos en la Tabla siguiente. Después, determine si los datos parecen estar relacionados linealmente.
| 0 | 2 | 4 | 6 | 8 | 10 |
| —105 | —50 | 1 | 55 | 105 | 160 |
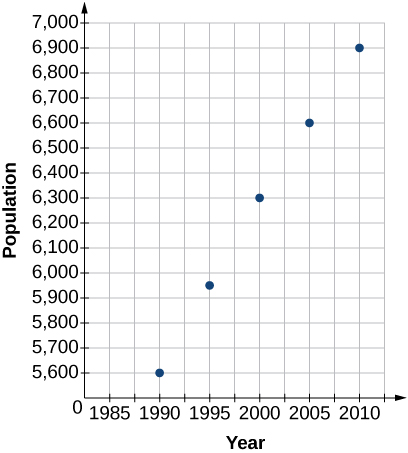
2) Dibujar un diagrama de dispersión para los datos en la Tabla. Si quisiéramos saber cuándo llegaría la población\(15,000\), ¿la respuesta implicaría interpolación o extrapolación?
| Año | Población |
|---|---|
| 1990 | 5,600 |
| 1995 | 5,950 |
| 2000 | 6,300 |
| 2005 | 6,600 |
| 2010 | 6,900 |
- Contestar
-
Extrapolación
3) Se pidió a ocho estudiantes que estimaran su puntaje en un cuestionario\(10\) de puntos. Sus puntuaciones estimadas y reales se dan en la Tabla. Trace los puntos y luego dibuje una línea que se ajuste a los datos.
| Predijo | Real |
|---|---|
| 6 | 6 |
| 7 | 7 |
| 7 | 8 |
| 8 | 8 |
| 7 | 9 |
| 9 | 10 |
| 10 | 10 |
| 10 | 9 |
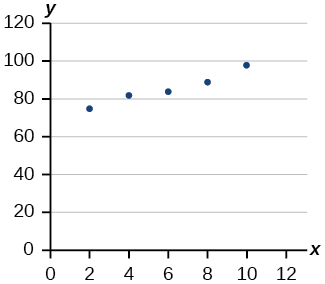
4) Dibuje una línea que mejor se ajuste a los datos trazados.
- Contestar
-
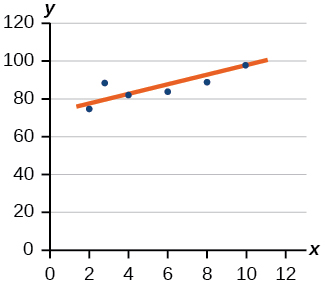
Para los ejercicios 5-6, considere los datos en la Tabla siguiente, que muestra el porcentaje de desempleados en una ciudad de personas de\(25\) años o más que son egresados universitarios se da a continuación, por año.
| Año | Porcentaje de egresados |
|---|---|
| 2000 | 6.5 |
| 2002 | 7.0 |
| 2005 | 7.4 |
| 2007 | 8.2 |
| 2010 | 9.0 |
5) Determinar si la tendencia parece ser lineal. Si es así, y suponiendo que la tendencia continúe, encontrar un modelo de regresión lineal para predecir el porcentaje de desempleados en un año determinado a tres decimales.
6) ¿En qué año superará el porcentaje\(12\%\)?
- Contestar
-
A mitad de camino hasta 2024
7) Con base en el conjunto de datos dados en la Tabla, calcular la línea de regresión utilizando una calculadora u otra herramienta tecnológica, y determinar el coeficiente de correlación a tres decimales.
| \(x\) | 17 | 20 | 23 | 26 | 29 |
|---|---|---|---|---|---|
| \(y\) | 15 | 25 | 31 | 37 | 40 |
8) Con base en el conjunto de datos dados en la Tabla, calcular la línea de regresión utilizando una calculadora u otra herramienta tecnológica, y determinar el coeficiente de correlación a tres decimales.
| \(x\) | 10 | 12 | 15 | 18 | 20 |
|---|---|---|---|---|---|
| \(y\) | 36 | 34 | 30 | 28 | 22 |
- Contestar
-
\(y=-1.294 x+49.412; r=-0.974\)
Para los ejercicios 9-12, considere este escenario: La población de una ciudad aumentó de manera constante en un lapso de diez años. Los siguientes pares ordenados muestran la población y el año en el lapso de diez años (población, año) para años específicos registrados:\((3,600,2000) ;(4,000,2001) ;(4,700,2003) ;(6,000,2006)\)
9) Utilizar regresión lineal para determinar una función\(y\), donde el año depende de la población, a tres decimales de precisión.
10) Predecir cuándo golpeará la población\(12,000\).
- Contestar
-
Principios de 2022
11) ¿Cuál es el coeficiente de correlación para este modelo con tres decimales de precisión?
12) Según el modelo, ¿cuál es la población en 2014?
- Contestar
-
\(7,660\)
Prueba de práctica
1) Determinar si la siguiente ecuación algebraica se puede escribir como una función lineal:\(2 x+3 y=7\)
- Contestar
-
Sí
2) Determinar si la siguiente función está aumentando o disminuyendo:\(f(x)=-2 x+5\)
3) Determinar si la siguiente función está aumentando o disminuyendo:\(f(x)=7 x+9\)
- Contestar
-
Incrementando
4) Dado el siguiente conjunto de información, encontrar una ecuación lineal que satisfaga las condiciones, si es posible. Pasa a través\((5,1)\) y\((3,-9)\)
5) Dado el siguiente conjunto de información, encontrar una ecuación lineal que satisfaga las condiciones, si es posible. \(x\)interceptar\((-4,0)\) y\(y\) -interceptar en\((0,-6)\)
- Contestar
-
\(y=-1.5 x-6\)
6) Encuentra la pendiente de la línea en la Figura a continuación.
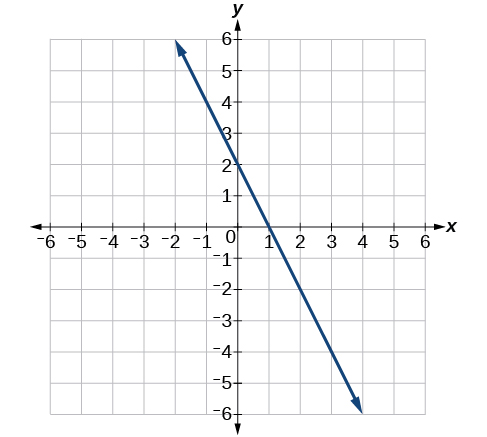
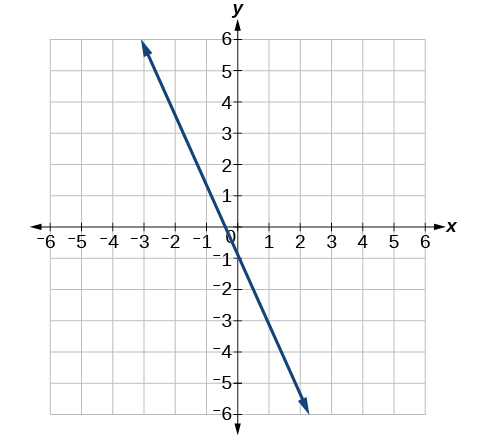
- Contestar
-
\(y=-2 x-1\)
8) ¿La Tabla representa una función lineal? Si es así, encuentra una ecuación lineal que modele los datos.
| \(x\) | —6 | 0 | 2 | 4 |
| \(g(x)\) | 14 | 32 | 38 | 44 |
9) ¿La Tabla representa una función lineal? Si es así, encuentra una ecuación lineal que modele los datos.
| \(x\) | 1 | 3 | 7 | 11 |
| \(g(x)\) | 4 | 9 | 19 | 12 |
- Contestar
-
No
10) A las 6 AM, una empresa en línea ha vendido\(120\) artículos ese día. Si la empresa vende un promedio de\(30\) artículos por hora por lo que resta del día, escriba una expresión para representar el número de artículos que se vendieron\(n\) después de las 6 AM.
Para los ejercicios 11-22, determine si las líneas dadas por las ecuaciones siguientes son paralelas, perpendiculares, o no paralelas ni perpendiculares:
11)\(\begin{align*}{y=\dfrac{3}{4} x-9} \\ {-4 x-3 y=8}\end{align*}\)
- Contestar
-
Perpendicular
12)\(\begin{align*}{-2 x+y=3} \\ {3 x+\dfrac{3}{2} y=5}\end{align*}\)
13) Encuentra las\(x\) - y\(y\) -intercepciones de la ecuación\(2 x+7 y=-14\).
- Contestar
-
\((-7,0) ;(0,-2)\)
14) A continuación se presentan descripciones de dos líneas. Encuentra las laderas de la Línea 1 y la Línea 2. ¿El par de líneas es paralelo, perpendicular, o ninguno?
La línea\(1 :\) pasa a través\((-2,-6)\) y\((3,14)\)
la línea\(2 :\) pasa a través\((2,6)\) y\((4,14)\)
15) Escribir una ecuación para una línea perpendicular al punto\(f(x)=4 x+3\) y que pasa por él\((8,10)\).
- Contestar
-
\(y=-0.25 x+12\)
16) Esbozar una línea con una\(y\) intersección\((0,5)\) y pendiente\(-\dfrac{5}{2}\).
17) Gráfica de la función lineal\(f(x)=-x+6\).
- Contestar
-
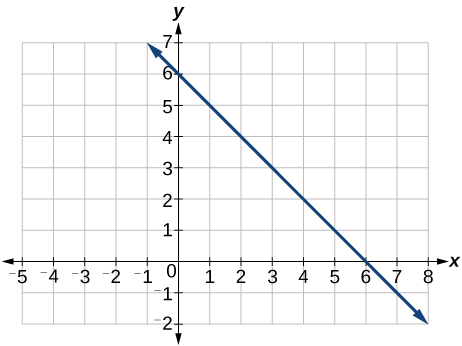
18) Para las dos funciones lineales, encuentre el punto de intersección:\(\begin{align*} x &=y+2 \\ 2x-3y &=-1 \end{align*}\)
19) Una empresa de renta de autos ofrece dos planes para rentar un auto.
Plan A:\(\$ 25\) por día y\(\$ 0.10\) por milla
Plan B:\(\$ 40\) por día con kilometraje ilimitado gratuito
¿Cuántas millas necesitarías conducir para el plan B para ahorrarte dinero?
- Contestar
-
\(150\)
20) Encontrar el área de un triángulo delimitada por el\(y\) eje, la línea\(f(x)=12-4 x,\) y la línea perpendicular a la\(f\) que pasa por el origen.
21) La población de un pueblo aumenta a un ritmo constante. En 2010 la población era\(65,000\). Para 2012 la población había aumentado a\(90,000\). Suponiendo que esta tendencia continúe, pronosticar la población en 2018.
- Contestar
-
\(165,000\)
22) El número de personas afligidas por el resfriado común en los meses de invierno disminuyó de manera constante\(25\) cada año desde 2002 hasta 2012. En 2002,\(8,040\) las personas fueron infligidas. Encuentra la función lineal que modela el número de personas afectadas por el resfriado\(C\) común en función del año,\(t\). ¿Cuándo se afligirá menos que la\(6,000\) gente?
Para los ejercicios 23-24, utilice la gráfica en Figura, mostrando el beneficio\(y\), en miles de dólares, de una empresa en un año determinado,\(x\), donde\(x\) representa años desde 1980.
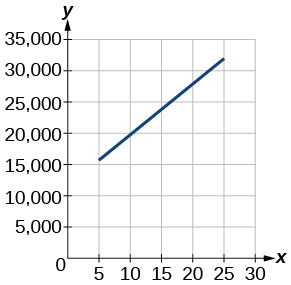
23) Encontrar la función lineal\(y\), donde\(y\) depende\(x\), el número de años desde 1980.
- Contestar
-
\(y=875 x+10,675\)
24) Encontrar e interpretar la\(y\) -intercepción.
25) En 2004, se encontraba una población escolar\(1250\). Para 2012 la población había bajado a\(875\). Supongamos que la población está cambiando linealmente.
- ¿Cuánto bajó la población entre el año 2004 y 2012?
- ¿Cuál es la disminución promedio de la población por año?
- Encontrar una ecuación para la población,\(P\), de los\(t\) años escolares posteriores a 2004.
- Contestar
-
- \(375\)
- bajó un promedio de\(46.875,\) o alrededor de\(47\) personas por año
- \(y=-46.875 t+1250\)
26) Dibujar un diagrama de dispersión para los datos proporcionados en la Tabla. Después, determine si los datos parecen estar relacionados linealmente.
| 0 | 2 | 4 | 6 | 8 | 10 |
| —450 | —200 | 10 | 265 | 500 | 755 |
27) Dibuje una línea de mejor ajuste para los datos trazados.
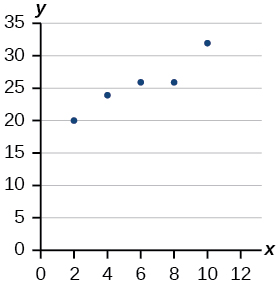
- Contestar
-
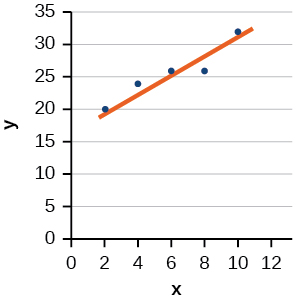
Para los ejercicios 28-29, utilice la Tabla a continuación, que muestra el porcentaje de personas desempleadas de\(25\) años o mayores que son egresados universitarios en una ciudad en particular, por año.
| Año | Porcentaje de egresados |
|---|---|
| 2000 | 8.5 |
| 2002 | 8.0 |
| 2005 | 7.2 |
| 2007 | 6.7 |
| 2010 | 6.4 |
28) Determinar si la tendencia aparece lineal. Si es así, y suponiendo que la tendencia continúe, encontrar un modelo de regresión lineal para predecir el porcentaje de desempleados en un año determinado a tres decimales.
29) ¿En qué año bajará el porcentaje\(4\%\)?
- Contestar
-
A principios de 2018
30) Con base en el conjunto de datos que se dan en la Tabla siguiente, calcular la línea de regresión utilizando una calculadora u otra herramienta tecnológica, y determinar el coeficiente de correlación. Redondear a tres decimales de precisión.
| \(x\) | 16 | 18 | 20 | 24 | 26 |
|---|---|---|---|---|---|
| \(y\) | 106 | 110 | 115 | 120 | 125 |
Para los ejercicios 31-33, considere este escenario: La población de una ciudad aumentó de manera constante en un lapso de diez años. Los siguientes pares ordenados muestran la población (en cientos) y el año en el lapso de diez años, (población, año) para años específicos registrados:\((4,500,2000) ;(4,700,2001) ;(5,200,2003) ;(5,800,2006)\)
31) Utilizar regresión lineal para determinar una función y, donde el año depende de la población. Redondear a tres decimales de precisión.
- Contestar
-
\(y=0.00455 x+1979.5\)
32) Predecir cuándo golpeará la población\(20,000\).
33) ¿Cuál es el coeficiente de correlación para este modelo?
- Contestar
-
\(r=0.999\)


