5.R: Funciones Trigonométricas (Revisión)

5.1: Ejercicios de revisión

Para los ejercicios 1-2, convierte las medidas de ángulo a grados.

1)$\dfrac{π}{4}$

Responder

$45°$

2)$−\dfrac{5π}{3}$

Para los ejercicios 3-6, convierte las medidas de ángulo en radianes.

3)$-210°$

Responder

$−\dfrac{7π}{6}$

4)$180°$

5) Encontrar la longitud de un arco en un círculo de$7$ metros de radio subtendido por el ángulo central de$85°$.

Responder

$10.385$metros

6) Encontrar el área del sector de un círculo con$32$ pies de diámetro y un ángulo de$\dfrac{3π}{5}$ radianes.

Para los ejercicios 7-8, encuentra el ángulo entre$0°$ y$360°$ que es coterminal con el ángulo dado.

7)$420°$

Responder

$60°$

8)$−80°$

Para los ejercicios 9-10, encuentra el ángulo entre$0$ y$2π$ en radianes que es coterminal con el ángulo dado.

9)$− \dfrac{20π}{11}$

Responder

$\dfrac{2π}{11}$

10)$\dfrac{14π}{5}$

Para los ejercicios 11-, dibuje el ángulo proporcionado en posición estándar sobre el plano cartesiano.

11)$-210°$

Responder

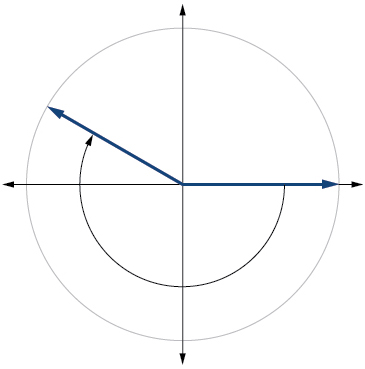
12)$75°$

13)$\dfrac{5π}{4}$

Responder

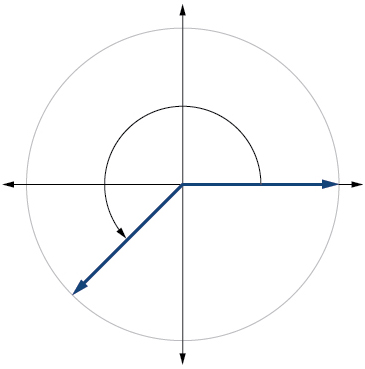
14)$−\dfrac{π}{3}$

15) Encuentra la velocidad lineal de un punto en el ecuador de la tierra si la tierra tiene un radio de$3,960$ millas y la tierra gira sobre su eje cada$24$ hora. Respuesta expresa en millas por hora.

Contestar

$1036.73$millas por hora

16) Una rueda de automóvil con un diámetro de$18$ pulgadas gira a la velocidad de$10$ revoluciones por segundo. ¿Cuál es la velocidad del auto en millas por hora?

5.2: Ejercicios de revisión

1) Encuentra el valor exacto de$\sin \dfrac{π}{3}$.

Responder

$\dfrac{\sqrt{3}}{2}$

2) Encuentra el valor exacto de$\cos \dfrac{π}{4}$.

3) Encuentra el valor exacto de$\cos π$.

Responder

$-1$

4) Indicar el ángulo de referencia para$300°$.

5) Indicar el ángulo de referencia para$\dfrac{3π}{4}$.

Responder

$\dfrac{π}{4}$

6) Calcular coseno de$330°$.

7) Cómpiese seno de$\dfrac{5π}{4}$.

Responder

$−\dfrac{\sqrt{2}}{2}$

8) Declarar el dominio de las funciones seno y coseno.

9) Indicar el rango de las funciones seno y coseno.

Responder

$[–1,1]$

5.3: Ejercicios de revisión

Para los ejercicios 1-4, encuentra el valor exacto de la expresión dada.

1)$\cos \dfrac{π}{6}$

2)$\tan \dfrac{π}{4}$

Responder

$1$

3)$\csc \dfrac{π}{3}$

4)$\sec \dfrac{π}{4}$

Responder

$\sqrt{2}$

Para los ejercicios 4-12, utilice ángulos de referencia para evaluar la expresión dada.

5)$\sec \dfrac{11π}{3}$

6)$\sec 315°$

Responder

$\sqrt{2}$

7) Si$\sec (t)=−2.5$, ¿cuál es el$\sec (−t)$?

8) Si$\tan (t)=−0.6$, ¿cuál es el$\tan (−t)$?

Responder

$0.6$

9) Si$\tan (t)=\dfrac{1}{3}$, encuentra$\tan (t−π)$.

10) Si$\cos (t)= \dfrac{\sqrt{2}}{2}$, encuentra$\sin (t+2π)$.

Responder

$\dfrac{\sqrt{2}}{2}$o$−\dfrac{\sqrt{2}}{2}$

11) ¿Qué funciones trigonométricas son paras?

12) ¿Qué funciones trigonométricas son impares?

Responder

seno, cosecante, tangente, cotangente

5.4: Ejercicios de revisión

Para los ejercicios 1-5, use longitudes laterales para evaluar.

1)$\cos \dfrac{π}{4}$

2)$\cot \dfrac{π}{3}$

Responder

$\dfrac{\sqrt{3}}{3}$

3)$\tan \dfrac{π}{6}$

4)$\cos (\dfrac{π}{2}) = \sin ( \_\_°)$

Responder

$0$

5)$\csc (18°)= \sec (\_\_°)$

Para los ejercicios 6-7, usa la información dada para encontrar las longitudes de los otros dos lados del triángulo rectángulo.

6)$\cos B= \dfrac{3}{5}, a=6$

Responder

$b=8,c=10$

7)$\tan A = \dfrac{5}{9},b=6$

Para los ejercicios 8-9, use la Figura a continuación para evaluar cada función trigonométrica.

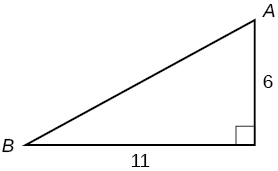
8)$\sin A$

Responder

$\dfrac{11\sqrt{157}}{157}$

9)$\tan B$

Para los ejercicios 10-11, resolver por los lados desconocidos del triángulo dado.

10)

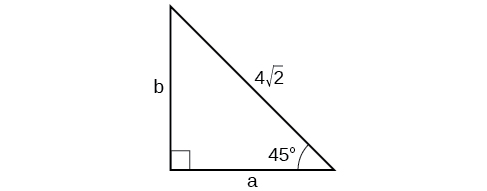
Responder

$a=4, b=4$

11)

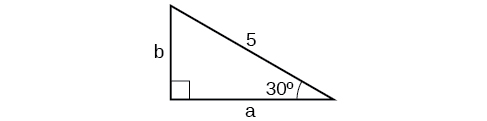
12) Una escalera$15$ de pies se apoya contra un edificio de manera que el ángulo entre el suelo y la escalera es$70°$. ¿Qué tan alto llega la escalera hasta el costado del edificio?

Responder

$14.0954$ft

13) El ángulo de elevación a la cima de un edificio en Baltimore se encuentra a$4$ grados del suelo a una distancia de$1$ milla de la base del edificio. Usando esta información, encuentra la altura del edificio.

Prueba de práctica

1) Convertir$\dfrac{5π}{6}$ radianes a grados.

Responder

$150°$

2) Convertir$−620°$ a radianes.

3) Encontrar la longitud de un arco circular con un radio$12$ centímetros subtendido por el ángulo central de$30°$.

Responder

$6.283$centímetros

4) Encontrar el área del sector con radio de$8$ pies y un ángulo de$\dfrac{5π}{4}$ radianes.

5) Encuentra el ángulo entre$0°$ y$360°$ que es coterminal con$375°$.

Responder

$15°$

6) Encuentra el ángulo entre$0$ y$2π$ en radianes que es coterminal con$−\dfrac{4π}{7}$.

7) Dibuja el ángulo$315°$ en posición estándar en el plano cartesiano.

Responder

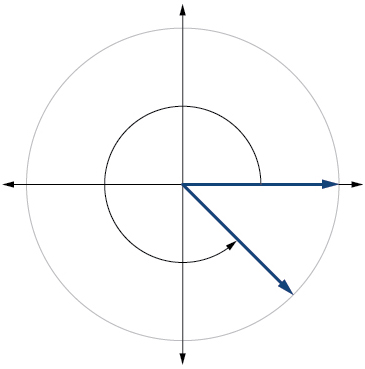
8) Dibuja el ángulo$−\dfrac{π}{6}$ en posición estándar en el plano cartesiano.

9) Un carnaval tiene una noria con un diámetro de$80$ pies. El tiempo para que la noria haga una revolución son$75$ segundos. ¿Cuál es la velocidad lineal en pies por segundo de un punto en la noria? ¿Cuál es la velocidad angular en radianes por segundo?

Responder

$3.351$pies por segundo,$\dfrac{2π}{75}$ radianes por segundo

10) Encuentra el valor exacto de$\sin \dfrac{π}{6}$.

11) Calcular seno de$240°$.

Responder

$−\dfrac{\sqrt{3}}{2}$

12) Declarar el dominio de las funciones seno y coseno.

13) Indicar el rango de las funciones seno y coseno.

Responder

$[ –1,1 ]$

14) Encuentra el valor exacto de$\cot \dfrac{π}{4}$.

15) Encuentra el valor exacto de$\tan \dfrac{π}{3}$.

Responder

$\sqrt{3}$

16) Utilizar ángulos de referencia para evaluar$\csc \dfrac{7π}{4}$.

17) Utilizar ángulos de referencia para evaluar$\tan 210°$.

Responder

$\dfrac{\sqrt{3}}{3}$

18) Si$\csc t=0.68$, ¿cuál es el$\csc (−t)$?

19) Si$\cos t= \dfrac{\sqrt{3}}{2}$, encuentra$\cos (t−2π)$.

Responder

$\dfrac{\sqrt{3}}{2}$

20) ¿Qué funciones trigonométricas son paras?

21) Encuentra el ángulo que falta:$\cos \left(\dfrac{\pi }{6} \right)= \sin (\;)$

Responder

$\dfrac{π}{3}$

22) Encuentra los lados faltantes del triángulo$ABC: \sin B= \dfrac{3}{4},c=12$

23) Encuentra los lados faltantes del triángulo.

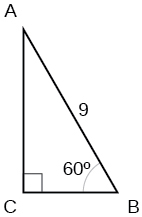
Responder

$a=\dfrac{9}{2},b=\dfrac{9\sqrt{3}}{2}$

24) El ángulo de elevación a la cima de un edificio en Chicago se encuentra a$9$ grados del suelo a una distancia de$2000$ pies de la base del edificio. Usando esta información, encuentra la altura del edificio.