13.4: Trigonometría de Triángulo Recto

Objetivos de aprendizaje

• Utilice triángulos rectos para evaluar las funciones trigonométricas.
• Encuentre valores de función para 30° (\(\dfrac{\pi}{6}\)) ,45° (\(\dfrac{\pi}{4}\)) y 60° (\(\dfrac{\pi}{3}\)).
• Utilizar cofunciones iguales de ángulos complementarios.
• Utilice las definiciones de funciones trigonométricas de cualquier ángulo.
• Utilice la trigonometría de triángulo rectángulo para resolver problemas aplicados.

Mt. El Everest, que se extiende a ambos lados de la frontera entre China y Nepal, es la montaña más alta del mundo. Medir su altura no es tarea fácil y, de hecho, la medición real ha sido fuente de controversia durante cientos de años. El proceso de medición implica el uso de triángulos y una rama de las matemáticas conocida como trigonometría. En esta sección, definiremos un nuevo grupo de funciones conocidas como funciones trigonométricas, y descubriremos cómo se pueden utilizar para medir alturas, como las de las montañas más altas.

Anteriormente hemos definido el seno y el coseno de un ángulo en términos de las coordenadas de un punto en el círculo unitario intersectado por el lado terminal del ángulo:

\[ \begin{align*} \cos t &= x \\ \sin t &=y \end{align*} \]

En esta sección, veremos otra forma de definir funciones trigonométricas usando propiedades de triángulos rectos.

Uso de triángulos rectos para evaluar funciones trigonométricas

En secciones anteriores, se utilizó un círculo unitario para definir las funciones trigonométricas. En esta sección, ampliaremos esas definiciones para que podamos aplicarlas a los triángulos rectos. El valor de la función sinusoidal o coseno de\(t\) es su valor en\(t\) radianes. Primero, necesitamos crear nuestro triángulo rectángulo. La figura\(\PageIndex{1}\) muestra un punto en un círculo unitario de radio 1. Si dejamos caer un segmento de línea vertical desde el punto\((x,y)\) hasta el eje x, tenemos un triángulo rectángulo cuyo lado vertical tiene longitud\(y\) y cuyo lado horizontal tiene longitud\(x\). Podemos usar este triángulo rectángulo para redefinir seno, coseno y otras funciones trigonométricas como proporciones de los lados de un triángulo rectángulo.

Figura\(\PageIndex{1}\)

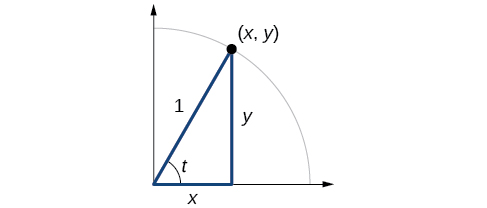
Sabemos

\[ \cos t= \frac{x}{1}=x \]

De igual manera, sabemos

\[ \sin t= \frac{y}{1}=y \]

Estas proporciones aún se aplican a los lados de un triángulo rectángulo cuando no hay ningún círculo unitario involucrado y cuando el triángulo no está en posición estándar y no se grafica usando\((x,y)\) coordenadas. Para poder usar estas relaciones libremente, daremos a los lados nombres más generales: En lugar de\(x\), llamaremos al lado entre el ángulo dado y el ángulo recto el lado adyacente al ángulo\(t\). (Adyacente significa “al lado”.) En lugar de\(y\), llamaremos al lado más distante del ángulo dado el lado opuesto de ángulo\(t\). Y en lugar de\(1\), llamaremos al lado de un triángulo rectángulo opuesto al ángulo recto la hipotenusa. Estos lados están etiquetados en la Figura\(\PageIndex{2}\).

Figura\(\PageIndex{2}\): Los lados de un triángulo rectángulo en relación con el ángulo\(t\).

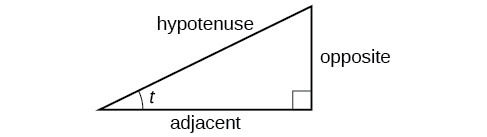
Comprender las relaciones del triángulo rectángulo

Dado un triángulo rectángulo con un ángulo agudo de\(t\),

\[\begin{align} \sin (t) &= \dfrac{\text{opposite}}{\text{hypotenuse}} \label{sindef}\\ \cos (t) &= \dfrac{\text{adjacent}}{\text{hypotenuse}} \label{cosdef}\\ \tan (t) &= \dfrac{\text{opposite}}{\text{adjacent}} \label{tandef}\end{align}\]

Un mnemotécnico común para recordar estas relaciones es SohCahtoA, formado a partir de las primeras letras de “S ine is o pposite over h ypotenuse, C osine is a djacent over h ypotenuse, T angent is o pposite over un djacente”.

cómo: Dadas las longitudes laterales de un triángulo rectángulo y uno de los ángulos agudos, encontrar el seno, el coseno y la tangente de ese ángulo

1. Encuentra el seno como la relación del lado opuesto a la hipotenusa.
2. Encuentra el coseno como la relación del lado adyacente a la hipotenusa.
3. Encontrar la tangente es la relación del lado opuesto al lado adyacente.

Ejemplo\(\PageIndex{1}\): Evaluating a Trigonometric Function of a Right Triangle

Dado el triángulo que se muestra en la Figura\(\PageIndex{3}\), encuentre el valor de\(\cos α\).

Figura\(\PageIndex{3}\)

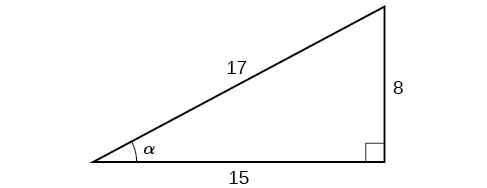
Solución

El lado adyacente al ángulo es 15, y la hipotenusa del triángulo es 17, así vía Ecuación\ ref {cosdef}:

\[\begin{align*} \cos (α) &= \dfrac{\text{adjacent}}{\text{hypotenuse}} \\[4pt] &= \dfrac{15}{17} \end{align*}\]

Ejercicio\(\PageIndex{1}\)

Dado el triángulo que se muestra en la Figura\(\PageIndex{4}\), encuentre el valor de\(\sin t\).

Figura\(\PageIndex{4}\)

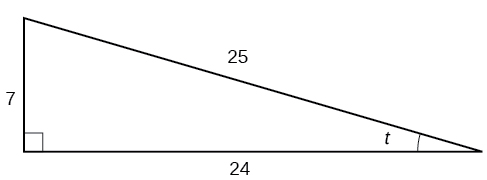
Contestar

\(\frac{7}{25}\)

Relación de ángulos y sus funciones

Cuando se trabaja con triángulos rectos, se aplican las mismas reglas independientemente de la orientación del triángulo. De hecho, podemos evaluar las seis funciones trigonométricas de cualquiera de los dos ángulos agudos en el triángulo en la Figura\(\PageIndex{5}\). El lado opuesto a un ángulo agudo es el lado adyacente al otro ángulo agudo, y viceversa.

Figura\(\PageIndex{5}\): El lado adyacente a un ángulo es opuesto al otro.

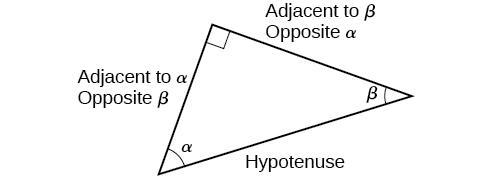
Se nos pedirá encontrar las seis funciones trigonométricas para un ángulo dado en un triángulo. Nuestra estrategia es encontrar primero el seno, el coseno y la tangente de los ángulos. Entonces, podemos encontrar fácilmente las otras funciones trigonométricas porque sabemos que el recíproco del seno es cosecante, el recíproco del coseno es secante y el recíproco de la tangente es cotangente.

cómo: Dadas las longitudes laterales de un triángulo rectángulo, evaluar las seis funciones trigonométricas de uno de los ángulos agudos

1. Si es necesario, dibuje el triángulo rectángulo y etiquete el ángulo proporcionado.
2. Identificar el ángulo, el lado adyacente, el lado opuesto al ángulo y la hipotenusa del triángulo rectángulo.
3. Encuentre la función requerida:
   • seno como la relación del lado opuesto a la hipotenusa
   • coseno como la relación del lado adyacente a la hipotenusa
   • tangente como la relación del lado opuesto al lado adyacente
   • secante como la relación entre la hipotenusa y el lado adyacente
   • cosecante como la relación entre la hipotenusa y el lado opuesto
   • cotangente como la relación del lado adyacente al lado opuesto

Ejemplo\(\PageIndex{2}\): Evaluating Trigonometric Functions of Angles Not in Standard Position

Usando el triángulo que se muestra en la Figura\(\PageIndex{6}\), evaluar\( \sin α, \cos α, \tan α, \sec α, \csc α,\) y\( \cot α\).

Figura\(\PageIndex{6}\)

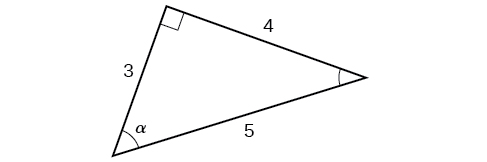
Solución

\[ \begin{align*} \sin α &= \dfrac{\text{opposite } α}{\text{hypotenuse}} = \dfrac{4}{5} \\ \cos α &= \dfrac{\text{adjacent to }α}{\text{hypotenuse}}=\dfrac{3}{5} \\ \tan α &= \dfrac{\text{opposite }α}{\text{adjacent to }α}=\dfrac{4}{3} \\ \sec α &= \dfrac{\text{hypotenuse}}{\text{adjacent to }α}= \dfrac{5}{3} \\ \csc α &= \dfrac{\text{hypotenuse}}{\text{opposite }α}=\dfrac{5}{4} \\ \cot α &= \dfrac{\text{adjacent to }α}{\text{opposite }α}=\dfrac{3}{4} \end{align*}\]

Ejercicio\(\PageIndex{2}\)

Usando el triángulo que se muestra en la Figura\(\PageIndex{7}\), evaluar\( \sin t, \cos t,\tan t, \sec t, \csc t,\) y\(\cot t\).

Figura\(\PageIndex{7}\)

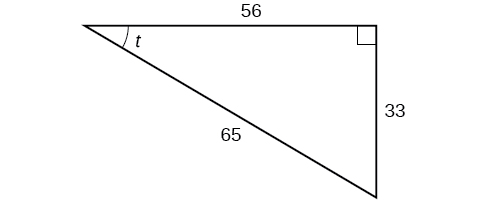
Contestar

\[\begin{align*} \sin t &= \frac{33}{65}, \cos t= \frac{56}{65},\tan t= \frac{33}{56}, \\ \\ \sec t &= \frac{65}{56},\csc t= \frac{65}{33},\cot t= \frac{56}{33} \end{align*}\]

Búsqueda de funciones trigonométricas de ángulos especiales usando longitudes laterales

Ya hemos discutido las funciones trigonométricas en cuanto se relacionan con los ángulos especiales en el círculo unitario. Ahora, podemos usar esas relaciones para evaluar triángulos que contienen esos ángulos especiales. Hacemos esto porque cuando evaluamos los ángulos especiales en funciones trigonométricas, tienen valores relativamente amigables, valores que contienen o no o solo una raíz cuadrada en la relación. Por lo tanto, estos son los ángulos que se suelen utilizar en los problemas de matemáticas y ciencias. Utilizaremos múltiplos de\(30°, 60°,\) y\(45°\), sin embargo, recordaremos que al tratar con triángulos rectos, estamos limitados a ángulos entre ellos\(0° \text{ and } 90°\).

Supongamos que tenemos un\(30°,60°,90°\) triángulo, que también puede describirse como un\(\frac{π}{6}, \frac{π}{3},\frac{π}{2}\) triángulo. Los lados tienen longitudes en la relación\(s,\sqrt{3}s,2s.\) Los lados de un\(45°,45°,90° \) triángulo, que también se puede describir como un\(\frac{π}{4},\frac{π}{4},\frac{π}{2}\) triángulo, tienen longitudes en la relación\(s,s,\sqrt{2}s.\) Estas relaciones se muestran en la Figura\(\PageIndex{8}\).

Figura\(\PageIndex{8}\): Longitudes laterales de triángulos especiales

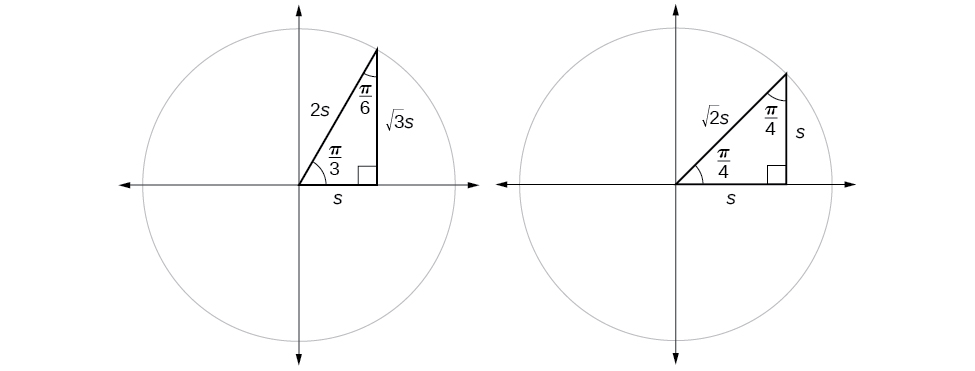
Luego podemos usar las proporciones de las longitudes de los lados para evaluar las funciones trigonométricas de ángulos especiales.

Dadas las funciones trigonométricas de un ángulo especial, evaluar usando longitudes laterales.

1. Utilice las longitudes laterales que se muestran en la Figura\(\PageIndex{8}\) para el ángulo especial que desea evaluar.
2. Utilice la relación de longitudes de lado apropiada a la función que desea evaluar.

Ejemplo\(\PageIndex{3}\): Evaluating Trigonometric Functions of Special Angles Using Side Lengths

Encuentra el valor exacto de las funciones trigonométricas de\(\frac{π}{3}\), usando longitudes laterales.

Solución

\[\begin{align*} \sin (\dfrac{π}{3}) &= \dfrac{\text{opp}}{\text{hyp}}=\dfrac{\sqrt{3}s}{2s}=\dfrac{\sqrt{3}}{2} \\ \cos (\dfrac{π}{3}) &= \dfrac{\text{adj}}{\text{hyp}}=\dfrac{s}{2s}=\dfrac{1}{2} \\ \tan (\dfrac{π}{3}) &= \dfrac{\text{opp}}{\text{adj}} =\dfrac{\sqrt{3}s}{s}=\sqrt{3} \\ \sec (\dfrac{π}{3}) &= \dfrac{\text{hyp}}{\text{adj}} = \dfrac{2s}{s}=2 \\ \csc (\dfrac{π}{3}) &= \dfrac{\text{hyp}}{\text{opp}} =\dfrac{2s}{\sqrt{3}s}=\dfrac{2}{\sqrt{3}}=\dfrac{2\sqrt{3}}{3} \\ \cot (\dfrac{π}{3}) &= \dfrac{\text{adj}}{\text{opp}}=\dfrac{s}{\sqrt{3}s}=\dfrac{1}{\sqrt{3}}=\dfrac{\sqrt{3}}{3} \end{align*}\]

Ejercicio\(\PageIndex{3}\)

Encuentra el valor exacto de las funciones trigonométricas del\(\frac{π}{4}\) uso de longitudes laterales.

Contestar

\( \sin (\frac{π}{4})=\frac{\sqrt{2}}{2}, \cos (\frac{π}{4})=\frac{\sqrt{2}}{2}, \tan (\frac{π}{4})=1,\)

\( \sec (\frac{π}{4})=\sqrt{2}, \csc (\frac{π}{4})=\sqrt{2}, \cot (\frac{π}{4}) =1 \)

Uso de igual cofunción de complementos

Si observamos más de cerca la relación entre el seno y el coseno de los ángulos especiales relativos al círculo unitario, notaremos un patrón. En un triángulo rectángulo con ángulos de\(\frac{π}{6}\) y\(\frac{π}{3}\), vemos que el seno de\(\frac{π}{3}\), es decir\(\frac{\sqrt{3}}{2}\), es también el coseno de\(\frac{π}{6}\), mientras que el seno de\(\frac{π}{6}\),\(\frac{1}{2},\) es decir también es el coseno de\(\frac{π}{3}\) (Figura\(\PageIndex{9}\)).

\[\begin{align*} \sin \frac{π}{3} &= \cos \frac{π}{6}=\frac{\sqrt{3}s}{2s}=\frac{\sqrt{3}}{2} \\ \sin \frac{π}{6} &= \cos \frac{π}{3}=\frac{s}{2s}=\frac{1}{2} \end{align*}\]

Figura\(\PageIndex{9}\): El seno de\(\frac{π}{3}\) es igual al coseno de\(\frac{π}{6}\) y viceversa.

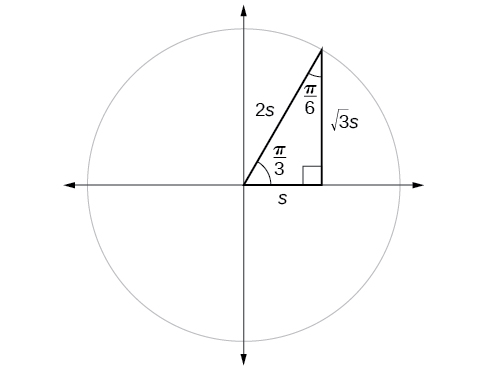
Este resultado no debería sorprendernos porque, como vemos en la Figura\(\PageIndex{9}\), el lado opuesto al ángulo de\(\frac{π}{3}\) es también el lado adyacente a\(\frac{π}{6}\), así\(\sin (\frac{π}{3})\) y\(\cos (\frac{π}{6})\) son exactamente la misma relación de los mismos dos lados,\(\sqrt{3} s\) y de\(2s.\) manera similar,\( \cos (\frac{π}{3})\) y\( \sin (\frac{π}{6})\) también son la misma proporción usando los mismos dos lados,\(s\) y\(2s\).

La interrelación entre los senos y los cosenos de\(\frac{π}{6}\) y\(\frac{π}{3}\) también se mantiene para los dos ángulos agudos en cualquier triángulo rectángulo, ya que en todos los casos, la relación de los mismos dos lados constituiría el seno de un ángulo y el coseno del otro. Dado que los tres ángulos de un triángulo se suman a π, π, y el ángulo recto es\(\frac{π}{2}\), los dos ángulos restantes también deben sumar\(\frac{π}{2}\). Eso significa que un triángulo rectángulo se puede formar con dos ángulos cualesquiera que se sumen a\(\frac{π}{2}\) —en otras palabras, dos ángulos complementarios cualesquiera. Entonces podemos afirmar una identidad de cofunción: Si dos ángulos cualesquiera son complementarios, el seno de uno es el coseno del otro, y viceversa. Esta identidad se ilustra en la Figura\(\PageIndex{10}\).

Figura\(\PageIndex{10}\): Identidad de cofunción de seno y coseno de ángulos complementarios

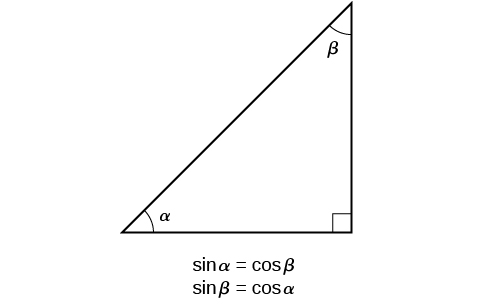
Usando esta identidad, podemos afirmar sin calcular, por ejemplo, que el seno de\(\frac{π}{12}\) es igual al coseno de\(\frac{5π}{12}\), y que el seno de\(\frac{5π}{12}\) es igual al coseno de\(\frac{π}{12}\). También podemos afirmar que si, para un cierto ángulo\(t, \cos t= \frac{5}{13},\) entonces\( \sin (\frac{π}{2}−t)=\frac{5}{13}\) también.

IDENTIDADES COFUNCIÓN

Las identidades de cofunción en radianes se listan en la Tabla\(\PageIndex{1}\).

Mesa\(\PageIndex{1}\)

\( \cos t= \sin (\frac{π}{2}−t)\)	\( \sin t= \cos (\dfrac{π}{2}−t)\)
\( \tan t= \cot (\dfrac{π}{2}−t) \)	\( \cot t= \tan (\dfrac{π}{2}−t)\)
\( \sec t= \csc (\dfrac{π}{2}−t) \)	\( \csc t= \sec (\dfrac{π}{2}−t)\)

cómo: Dado el seno y el coseno de un ángulo, encontrar el seno o coseno de su complemento.

1. Para encontrar el seno del ángulo complementario, encuentra el coseno del ángulo original.
2. Para encontrar el coseno del ángulo complementario, encuentra el seno del ángulo original.

Ejemplo\(\PageIndex{4}\): Using Cofunction Identities

Si\( \sin t = \frac{5}{12},\) encuentra\(( \cos \frac{π}{2}−t)\).

Solución

Según las identidades de cofunción para seno y coseno,

\[ \sin t= \cos (\dfrac{π}{2}−t). \nonumber\]

Entonces

\[ \cos (\dfrac{π}{2}−t)= \dfrac{5}{12}. \nonumber\]

Ejercicio\(\PageIndex{4}\)

Si\(\csc (\frac{π}{6})=2,\) encuentra\( \sec (\frac{π}{3}).\)

Solución

2

Uso de funciones trigonométricas

En ejemplos anteriores, evaluamos el seno y el coseno en triángulos donde conocíamos los tres lados. Pero el verdadero poder de la trigonometría del triángulo rectángulo surge cuando miramos triángulos en los que conocemos un ángulo pero no conocemos todos los lados.

cómo: Dado un triángulo rectángulo, la longitud de un lado y la medida de un ángulo agudo, encontrar los lados restantes

1. Para cada lado, seleccione la función trigonométrica que tiene el lado desconocido como numerador o denominador. El lado conocido será a su vez el denominador o el numerador.
2. Escribe una ecuación que establezca el valor de función del ángulo conocido igual a la relación de los lados correspondientes.
3. Usando el valor de la función trigonométrica y la longitud lateral conocida, resuelva la longitud lateral faltante.

Ejemplo\(\PageIndex{5}\): Finding Missing Side Lengths Using Trigonometric Ratios

Encuentra los lados desconocidos del triángulo en la Figura\(\PageIndex{11}\).

Figura\(\PageIndex{11}\)

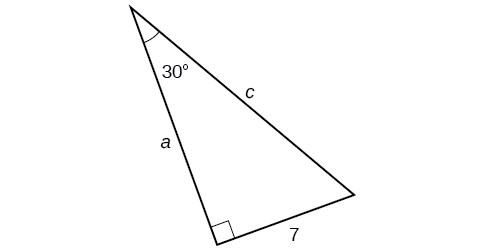
Solución

Conocemos el ángulo y el lado opuesto, por lo que podemos usar la tangente para encontrar el lado adyacente.

\[ \tan (30°)= \dfrac{7}{a} \nonumber\]

Reorganizamos para resolver para\(a\).

\[\begin{align} a &=\dfrac{7}{ \tan (30°)} \\ & =12.1 \end{align} \nonumber\]

Podemos usar el seno para encontrar la hipotenusa.

\[ \sin (30°)= \dfrac{7}{c} \nonumber\]

Nuevamente, reorganizamos para resolver para\(c\).

\[\begin{align*} c &= \dfrac{7}{\sin (30°)} =14 \end{align*}\]

Ejercicio\(\PageIndex{5}\):

Un triángulo rectángulo tiene un ángulo de\(\frac{π}{3}\) y una hipotenusa de 20. Encuentra los lados desconocidos y el ángulo del triángulo.

Contestar

\(\mathrm{adjacent=10; opposite=10 \sqrt{3}; }\)falta el ángulo es\(\frac{π}{6}\)

Uso de la trigonometría de triángulo recto para resolver problemas aplicados

La trigonometría de triángulo rectángulo tiene muchas aplicaciones prácticas. Por ejemplo, la capacidad de calcular las longitudes de los lados de un triángulo permite encontrar la altura de un objeto alto sin subir a la cima o tener que extender una cinta métrica a lo largo de su altura. Lo hacemos midiendo una distancia desde la base del objeto hasta un punto en el suelo a cierta distancia, donde podemos mirar hacia arriba hasta la parte superior del objeto alto en ángulo. El ángulo de elevación de un objeto por encima de un observador en relación con el observador es el ángulo entre la horizontal y la línea desde el objeto hasta el ojo del observador. El triángulo rectángulo que crea esta posición tiene lados que representan la altura desconocida, la distancia medida desde la base y la línea de visión en ángulo desde el suelo hasta la parte superior del objeto. Conociendo la distancia medida a la base del objeto y el ángulo de la línea de visión, podemos usar funciones trigonométricas para calcular la altura desconocida. De igual manera, podemos formar un triángulo desde la parte superior de un objeto alto mirando hacia abajo. El ángulo de depresión de un objeto debajo de un observador en relación con el observador es el ángulo entre la horizontal y la línea desde el objeto hasta el ojo del observador. Ver Figura\(\PageIndex{12}\).

Figura\(\PageIndex{12}\)

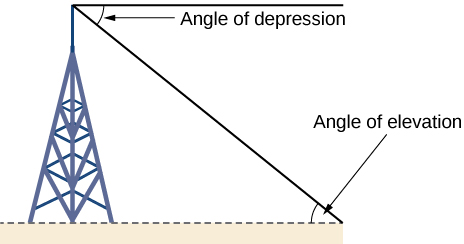
cómo: Dado un objeto alto, medir su altura indirectamente

1. Haga un boceto de la situación problemática para realizar un seguimiento de la información conocida y desconocida.
2. Coloque una distancia medida desde la base del objeto hasta un punto donde la parte superior del objeto sea claramente visible.
3. En el otro extremo de la distancia medida, mire hacia arriba hasta la parte superior del objeto. Mida el ángulo que hace la línea de visión con la horizontal.
4. Escribe una ecuación que relacione la altura desconocida, la distancia medida y la tangente del ángulo de la línea de visión.
5. Resuelve la ecuación para la altura desconocida.

Ejemplo\(\PageIndex{6}\): Measuring a Distance Indirectly

Para encontrar la altura de un árbol, una persona camina hasta un punto a 30 pies de la base del árbol. Mide un ángulo de 57° 57° entre una línea de visión a la parte superior del árbol y el suelo, como se muestra en la Figura\(\PageIndex{13}\). Encuentra la altura del árbol.

Figura\(\PageIndex{13}\)

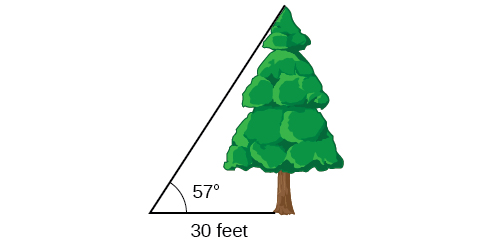
Solución

Sabemos que el ángulo de elevación es\(57°\) y el lado adyacente tiene 30 pies de largo. El lado opuesto es la altura desconocida.

La función trigonométrica que relaciona el lado opuesto a un ángulo y el lado adyacente al ángulo es la tangente. Por lo que vamos a exponer nuestra información en términos de la tangente de\(57°\), dejando\(h\) ser la altura desconocida.

\[\begin{array}{cl} \tan θ = \dfrac{\text{opposite}}{\text{adjacent}} & \text{} \\ \tan (57°) = \dfrac{h}{30} & \text{Solve for }h. \\ h=30 \tan (57°) & \text{Multiply.} \\ h≈46.2 & \text{Use a calculator.} \end{array} \]

El árbol mide aproximadamente 46 pies de altura.

Ejercicio\(\PageIndex{6}\):

¿Cuánto tiempo se necesita una escalera para llegar a un alféizar de una ventana a 50 pies sobre el suelo si la escalera descansa contra el edificio haciendo un ángulo\(\frac{5π}{12}\) con el suelo? Redondear al pie más cercano.

Contestar

Cerca de 52 pies

medios de comunicación:

Acceda a estos recursos en línea para obtener instrucción adicional y práctica con trigonometría de triángulo rectángulo.

• Encontrar funciones trigonométricas en la calculadora
• Encontrar funciones trigonométricas usando un triángulo recto
• Relacionar funciones trigonométricas con lados de un triángulo recto
• Determine seis funciones trigonométricas a partir de un triángulo
• Determinar la longitud del lado del triángulo recto

Visite este sitio web para obtener preguntas de práctica adicionales de Learningpod.

Ecuaciones Clave

Identidades de cofunción

\[\begin{align*} \cos t &= \sin ( \frac{π}{2}−t) \\ \sin t &= \cos (\frac{π}{2}−t) \\ \tan t &= \cot (\frac{π}{2}−t) \\ \cot t &= \tan (\frac{π}{2}−t) \\ \sec t &= \csc (\frac{π}{2}−t) \\ \csc t &= \sec (\frac{π}{2}−t) \end{align*}\]

Conceptos clave

• Podemos definir funciones trigonométricas como relaciones de las longitudes laterales de un triángulo rectángulo. Ver Ejemplo.
• Las mismas longitudes laterales se pueden utilizar para evaluar las funciones trigonométricas de cualquier ángulo agudo en un triángulo rectángulo. Ver Ejemplo.
• Podemos evaluar las funciones trigonométricas de ángulos especiales, conociendo las longitudes laterales de los triángulos en los que ocurren. Ver Ejemplo.
• Dos ángulos complementarios cualesquiera podrían ser los dos ángulos agudos de un triángulo rectángulo.
• Si dos ángulos son complementarios, las identidades de cofunción establecen que el seno de uno es igual al coseno del otro y viceversa. Ver Ejemplo.
• Podemos usar funciones trigonométricas de un ángulo para encontrar longitudes de lado desconocidas.
• Seleccione la función trigonométrica que representa la relación entre el lado desconocido y el lado conocido. Ver Ejemplo.
• La trigonometría del triángulo rectángulo permite la medición de alturas y distancias inaccesibles.
• La altura o distancia desconocida se puede encontrar creando un triángulo rectángulo en el que la altura o distancia desconocida es uno de los lados, y se conocen otro lado y ángulo. Ver Ejemplo.

Glosario

lado adyacente

en un triángulo recto, el lado entre un ángulo dado y el ángulo recto

ángulo de depresión

el ángulo entre la horizontal y la línea desde el objeto hasta el ojo del observador, suponiendo que el objeto está colocado más bajo que el observador

ángulo de elevación

el ángulo entre la horizontal y la línea desde el objeto hasta el ojo del observador, asumiendo que el objeto está colocado más alto que el observador

lado opuesto

en un triángulo rectángulo, el lado más distante de un ángulo dado

hipotenusa

el lado de un triángulo rectángulo opuesto al ángulo recto