13.E: Funciones trigonométricas (Ejercicios)
- Page ID
- 121478
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)5.1: Ángulos
En esta sección, examinaremos las propiedades de los ángulos.
Verbal
1) Dibuja un ángulo en posición estándar. Etiquete el vértice, el lado inicial y el lado terminal.
- Responder
-
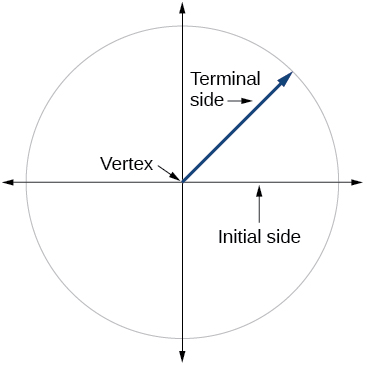
2) Explique por qué hay un número infinito de ángulos que son coterminales a cierto ángulo.
3) Indicar lo que significa un ángulo positivo o negativo, y explicar cómo dibujar cada uno.
- Responder
-
Si el ángulo es positivo o negativo determina la dirección. Se dibuja un ángulo positivo en el sentido contrario a las agujas del reloj y se dibuja un ángulo negativo en el sentido de las agujas del reloj.
4) ¿Cómo se compara la medida radianes de un ángulo con la medida de grado? Incluya una explicación de\(1\) radián en su párrafo.
5) Explicar las diferencias entre la velocidad lineal y la velocidad angular al describir el movimiento a lo largo de una trayectoria circular.
- Responder
-
La velocidad lineal es una medida que se encuentra calculando la distancia de un arco en comparación con el tiempo. La velocidad angular es una medida que se encuentra calculando el ángulo de un arco en comparación con el tiempo.
Gráfica
Para los ejercicios 6-21, dibuja un ángulo en posición estándar con la medida dada.
6)\(30^{\circ}\)
7)\(300^{\circ}\)
- Responder
-
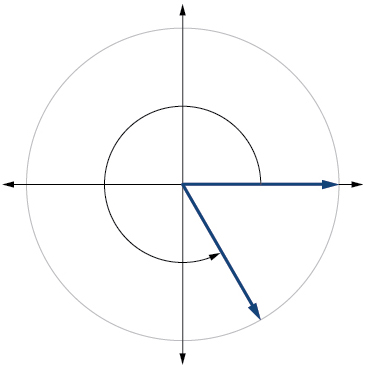
8)\(-80^{\circ}\)
9)\(135^{\circ}\)
- Responder
-
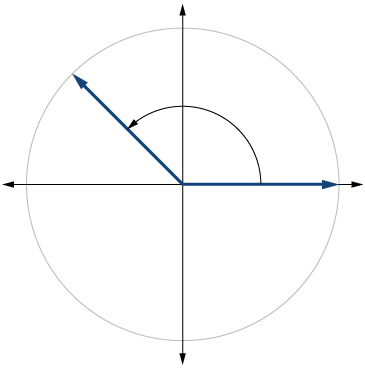
10)\(-150^{\circ}\)
11)\(\dfrac{2π}{3}\)
- Responder
-
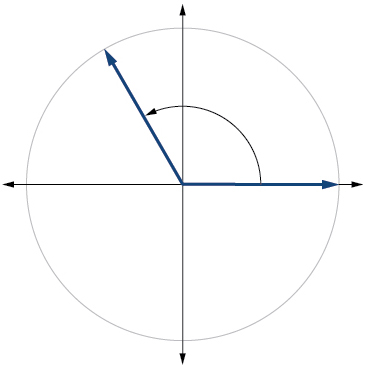
12)\(\dfrac{7π}{4}\)
13)\(\dfrac{5π}{6}\)
- Responder
-
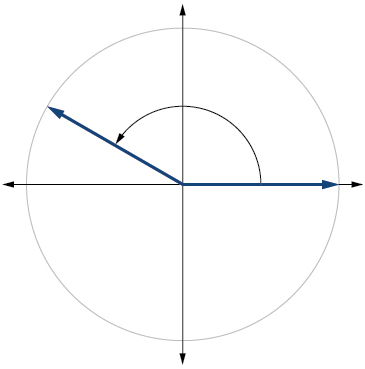
14)\(\dfrac{π}{2}\)
15)\(−\dfrac{π}{10}\)
- Responder
-
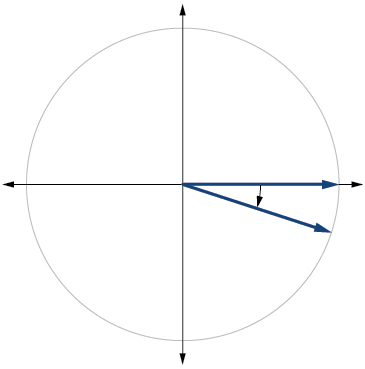
16)\(415^{\circ}\)
17)\(-120^{\circ}\)
- Responder
-
\(240^{\circ}\)
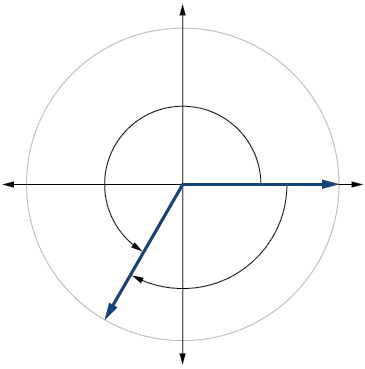
18)\(-315^{\circ}\)
19)\(\dfrac{22π}{3}\)
- Responder
-
\(\dfrac{4π}{3}\)
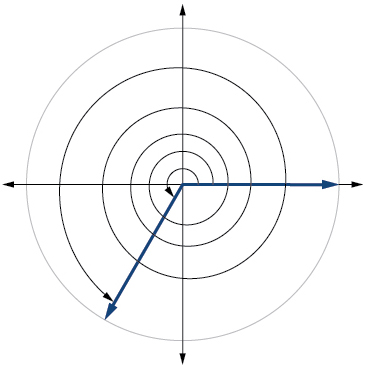
20)\(−\dfrac{π}{6}\)
21)\(−\dfrac{4π}{3}\)
- Responder
-
\(\dfrac{2π}{3}\)
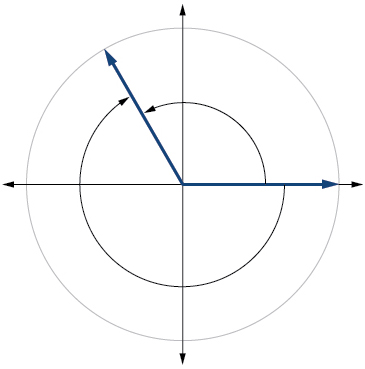
Para los ejercicios 22-23, refiérase a la Figura a continuación. Redondear a dos decimales.
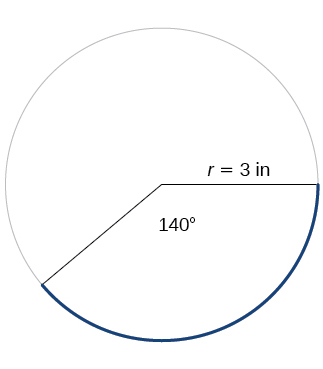
22) Encuentra la longitud del arco.
23) Encontrar la zona del sector.
- Responder
-
\(\dfrac{27π}{2}≈11.00 \text{ in}^2\)
Para los ejercicios 24-25, consulte la Figura a continuación. Redondear a dos decimales.
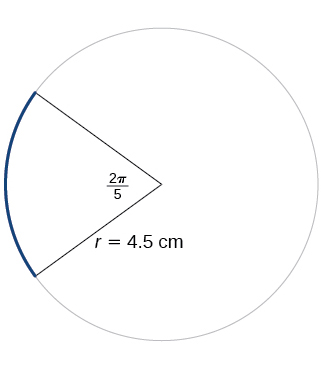
24) Encuentra la longitud del arco.
25) Encontrar la zona del sector.
- Responder
-
\(\dfrac{81π}{20}≈12.72\text{ cm}^2\)
Algebraico
Para los ejercicios 26-32, convertir los ángulos en radianes a grados.
26)\(\dfrac{3π}{4}\) radianes
27)\(\dfrac{π}{9}\) radianes
- Responder
-
\(20^{\circ}\)
28)\(−\dfrac{5π}{4}\) radianes
29)\(\dfrac{π}{3}\) radianes
- Responder
-
\(60^{\circ}\)
30)\(−\dfrac{7π}{3}\) radianes
31)\(−\dfrac{5π}{12}\) radianes
- Responder
-
\(-75^{\circ}\)
32)\(\dfrac{11π}{6}\) radianes
Para los ejercicios 33-39, convertir los ángulos en grados a radianes.
33)\(90^{\circ}\)
- Responder
-
\(\dfrac{π}{2}\)radianes
34)\(100^{\circ}\)
35)\(-540^{\circ}\)
- Responder
-
\(−3π\)radianes
36)\(-120^{\circ}\)
37)\(180^{\circ}\)
- Responder
-
\(π\)radianes
38)\(-315^{\circ}\)
39)\(150^{\circ}\)
- Responder
-
\(\dfrac{5π}{6}\)radianes
Para los ejercicios 40-45, utilice para dar información para encontrar la longitud de un arco circular. Redondear a dos decimales.
40) Encuentra la longitud del arco de un círculo de\(12\) pulgadas de radio subtendido por un ángulo central de\(\dfrac{π}{4}\) radianes.
41) Encuentra la longitud del arco de un círculo de radio\(5.02\) millas subtendido por el ángulo central de\(\dfrac{π}{3}\).
- Responder
-
\(\dfrac{5.02π}{3}≈5.26\)millas
42) Encontrar la longitud del arco de un círculo de\(14\) metros de diámetro subtendido por el ángulo central de\(\dfrac{5\pi }{6}\).
43) Encuentra la longitud del arco de un círculo de\(10\) centímetros de radio subtendido por el ángulo central de\(50^{\circ}\).
- Responder
-
\(\dfrac{25π}{9}≈8.73\)centímetros
44) Encuentra la longitud del arco de un círculo de\(5\) pulgadas de radio subtendido por el ángulo central de\(220^{circ}\).
45) Encontrar la longitud del arco de un círculo de\(12\) metros de diámetro subtendido por el ángulo central es\(63^{circ}\).
- Responder
-
\(\dfrac{21π}{10}≈6.60\)metros
Para los ejercicios 46-49, utilice la información dada para encontrar el área del sector. Redondear a cuatro decimales.
46) Un sector de un círculo tiene un ángulo central de\(45^{\circ}\) y un radio\(6\) cm.
47) Un sector de un círculo tiene un ángulo central de\(30^{\circ}\) y un radio de\(20\) cm.
- Responder
-
\(104.7198\; cm^2\)
48) Un sector de círculo con\(10\) pies de diámetro y un ángulo de\(\dfrac{π}{2}\) radianes.
49) Un sector de círculo con radio de\(0.7\) pulgadas y un ángulo de\(π\) radianes.
- Responder
-
\(0.7697\; in^2\)
Para los ejercicios 50-53, encuentra el ángulo entre\(0^{\circ}\) y\(360^{\circ}\) que es coterminal al ángulo dado.
50)\(-40^{\circ}\)
51)\(-110^{\circ}\)
- Responder
-
\(250^{\circ}\)
52)\(700^{\circ}\)
53)\(1400^{\circ}\)
- Responder
-
\(320^{\circ}\)
Para los ejercicios 54-57, encuentra el ángulo entre\(0\) y\(2\pi \) en radianes que es coterminal al ángulo dado.
54)\(−\dfrac{π}{9}\)
55)\(\dfrac{10π}{3}\)
- Responder
-
\(\dfrac{4π}{3}\)
56)\(\dfrac{13π}{6}\)
57)\(\dfrac{44π}{9}\)
- Responder
-
\(\dfrac{8π}{9}\)
Aplicaciones del mundo real
58) Un camión con ruedas de\(32\) -pulgadas de diámetro se desplaza a\(60\) mi/h. Encuentra la velocidad angular de las ruedas en rad/min. ¿Cuántas revoluciones por minuto hacen las ruedas?
59) Una bicicleta con ruedas de\(24\) -pulgadas de diámetro se desplaza a\(15\) mi/h. Encuentra la velocidad angular de las ruedas en rad/min. ¿Cuántas revoluciones por minuto hacen las ruedas?
- Responder
-
\(1320\)rad\(210.085\) RPM
60) Una rueda de\(8\) pulgadas de radio está girando\(15^{\circ}/s\). ¿Cuál es la velocidad lineal\(v\), la velocidad angular en RPM y la velocidad angular en rad/s?
61) Una rueda de\(14\) pulgadas de radio está girando\(0.5 \text{rad/s}\). ¿Cuál es la velocidad lineal\(v\), la velocidad angular en RPM y la velocidad angular en grados/s?
- Responder
-
\(7\)en. /s,\(4.77\) RPM,\(28.65\) grados/s
62) Un CD tiene un diámetro de\(120\) milímetros. Al reproducir audio, la velocidad angular varía para mantener constante la velocidad lineal donde se está leyendo el disco. Al leer a lo largo del borde exterior del disco, la velocidad angular es de aproximadamente\(200\) RPM (revoluciones por minuto). Encuentra la velocidad lineal.
63) Cuando se quema en una unidad de CD-R grabable, la velocidad angular de un CD suele ser mucho más rápida que cuando se reproduce audio, pero la velocidad angular aún varía para mantener constante la velocidad lineal donde se está escribiendo el disco. Al escribir a lo largo del borde exterior del disco, la velocidad angular de una unidad es de aproximadamente\(4800\) RPM (revoluciones por minuto). Encuentra la velocidad lineal si el CD tiene un diámetro de\(120\) milímetros.
- Responder
-
\(1,809,557.37 \text{ mm/min}=30.16 \text{ m/s}\)
64) Una persona se encuentra de pie en el ecuador de la Tierra (radio\(3960\) millas). ¿Cuáles son sus velocidades lineales y angulares?
65) Encontrar la distancia a lo largo de un arco en la superficie de la Tierra que subtiende un ángulo central de\(5\) minutos\((1 \text{ minute}=\dfrac{1}{60} \text{ degree})\). El radio de la Tierra es\(3960\) millas.
- Responder
-
\(5.76\)millas
66) Encontrar la distancia a lo largo de un arco en la superficie de la Tierra que subtiende un ángulo central de\(7\) minutos\((1 \text{ minute}=\dfrac{1}{60} \text{ degree})\). El radio de la Tierra es\(3960\) millas.
67) Considera un reloj con manecilla de hora y minutero. ¿Cuál es la medida del ángulo que la manecilla minutera traza en\(20\) minutos?
- Responder
-
\(120°\)
Extensiones
68) Dos ciudades tienen la misma longitud. La latitud de la ciudad A es\(9.00\) grados norte y la latitud de la ciudad B es\(30.00\) grado norte. Supongamos que el radio de la tierra es\(3960\) millas. Encuentra la distancia entre las dos ciudades.
69) Una ciudad se ubica a\(40\) grados de latitud norte. Supongamos que el radio de la tierra es\(3960\) millas y la tierra gira una vez cada\(24\) hora. Encuentra la velocidad lineal de una persona que reside en esta ciudad.
- Responder
-
\(794\)millas por hora
70) Una ciudad se ubica a\(75\) grados de latitud norte. Supongamos que el radio de la tierra es\(3960\) millas y la tierra gira una vez cada\(24\) hora. Encuentra la velocidad lineal de una persona que reside en esta ciudad.
71) Encuentra la velocidad lineal de la luna si la distancia promedio entre la tierra y la luna es de\(239,000\) millas, asumiendo que la órbita de la luna es circular y requiere aproximadamente\(28\) días. Respuesta expresa en millas por hora.
- Responder
-
\(2,234\)millas por hora
72) Una bicicleta tiene llantas en\(28\) pulgadas de diámetro. Un tacómetro determina que las ruedas están girando a\(180\) RPM (revoluciones por minuto). Encuentra la velocidad que recorre la bicicleta por la carretera.
73) Un automóvil recorre\(3\) millas. Sus llantas hacen\(2640\) revoluciones. ¿Cuál es el radio de una llanta en pulgadas?
- Responder
-
\(11.5\)pulgadas
74) Una rueda en un tractor tiene un diámetro de\(24\) -pulgada. ¿Cuántas revoluciones hace la rueda si el tractor recorre\(4\) millas?
5.2: Círculo unitario - Funciones de seno y coseno
Verbal
1) Describir el círculo unitario.
- Responder
-
El círculo unitario es un círculo de radio\(1\) centrado en el origen.
2) ¿Qué representan las\(y\) coordenadas\(x\) - y -de los puntos del círculo unitario?
3) Discutir la diferencia entre un ángulo coterminal y un ángulo de referencia.
- Responder
-
Los ángulos coterminales son ángulos que comparten el mismo lado terminal. Un ángulo de referencia es el tamaño del ángulo agudo más pequeño\(t\),, formado por el lado terminal del ángulo\(t\) y el eje horizontal.
4) Explicar cómo el coseno de un ángulo en el segundo cuadrante difiere del coseno de su ángulo de referencia en el círculo unitario.
5) Explicar cómo el seno de un ángulo en el segundo cuadrante difiere del seno de su ángulo de referencia en el círculo unitario.
- Responder
-
Los valores sinusoidales son iguales.
Algebraico
Para los ejercicios 6-9, utilizar el signo dado de las funciones seno y coseno para encontrar el cuadrante en el que se\(t\) encuentra el punto terminal determinado por.
6)\( \sin (t)<0\) y\( \cos (t)<0\)
7)\( \sin (t)>0\) y\( \cos (t)>0\)
- Responder
-
\(\textrm{I}\)
8)\( \sin (t)>0 \) y\( \cos (t)<0\)
9)\( \sin (t)<0 \) y\( \cos (t)>0\)
- Responder
-
\(\textrm{IV}\)
Para los ejercicios 10-22, encuentra el valor exacto de cada función trigonométrica.
10)\(\sin \dfrac{π}{2}\)
11)\(\sin \dfrac{π}{3}\)
- Responder
-
\(\dfrac{\sqrt{3}}{2}\)
12)\( \cos \dfrac{π}{2}\)
13)\( \cos \dfrac{π}{3}\)
- Responder
-
\(\dfrac{1}{2}\)
14)\( \sin \dfrac{π}{4}\)
15)\( \cos \dfrac{π}{4}\)
- Responder
-
\(\dfrac{\sqrt{2}}{2}\)
16)\( \sin \dfrac{π}{6}\)
17)\( \sin π\)
- Responder
-
\(0\)
18)\( \sin \dfrac{3π}{2}\)
19)\( \cos π\)
- Responder
-
\(−1\)
20)\( \cos 0\)
21)\(cos \dfrac{π}{6}\)
- Responder
-
\(\dfrac{\sqrt{3}}{2}\)
22)\( \sin 0\)
Numérico
Para los ejercicios 23-33, indicar el ángulo de referencia para el ángulo dado.
23)\(240°\)
- Responder
-
\(60°\)
24)\(−170°\)
25)\(100°\)
- Responder
-
\(80°\)
26)\(−315°\)
27)\(135°\)
- Responder
-
\(45°\)
28)\(\dfrac{5π}{4}\)
29)\(\dfrac{2π}{3}\)
- Responder
-
\(\dfrac{π}{3}\)
30)\(\dfrac{5π}{6}\)
31)\(−\dfrac{11π}{3}\)
- Responder
-
\(\dfrac{π}{3}\)
32)\(\dfrac{−7π}{4}\)
33)\(\dfrac{−π}{8}\)
- Responder
-
\(\dfrac{π}{8}\)
Para los ejercicios 34-49, encuentra el ángulo de referencia, el cuadrante del lado terminal, y el seno y coseno de cada ángulo. Si el ángulo no es uno de los ángulos en el círculo unitario, use una calculadora y redondee a tres decimales.
34)\(225°\)
35)\(300°\)
- Responder
-
\(60°\), Cuadrante IV,\( \sin (300°)=−\dfrac{\sqrt{3}}{2}, \cos (300°)=\dfrac{1}{2}\)
36)\(320°\)
37)\(135°\)
- Responder
-
\(45°\), Cuadrante II,\( \sin (135°)=\dfrac{\sqrt{2}}{2}, \cos (135°)=−\dfrac{\sqrt{2}}{2}\)
38)\(210°\)
39)\(120°\)
- Responder
-
\(60°\), Cuadrante II,\(\sin (120°)=\dfrac{\sqrt{3}}{2}\),\(\cos (120°)=−\dfrac{1}{2}\)
40)\(250°\)
41)\(150°\)
- Responder
-
\(30°\), Cuadrante II,\( \sin (150°)=\frac{1}{2}\),\(\cos(150°)=−\dfrac{\sqrt{3}}{2}\)
42)\(\dfrac{5π}{4}\)
43)\(\dfrac{7π}{6}\)
- Responder
-
\(\dfrac{π}{6}\), Cuadrante III,\(\sin \left( \dfrac{7π}{6}\right )=−\dfrac{1}{2}\),\(\cos \left (\dfrac{7π}{6} \right)=−\dfrac{\sqrt{3}}{2}\)
44)\(\dfrac{5π}{3}\)
45)\(\dfrac{3π}{4}\)
- Responder
-
\(\dfrac{π}{4}\), Cuadrante II,\(\sin \left(\dfrac{3π}{4}\right)=\dfrac{\sqrt{2}}{2}\),\(\cos\left(\dfrac{4π}{3}\right)=−\dfrac{\sqrt{2}}{2}\)
46)\(\dfrac{4π}{3}\)
47)\(\dfrac{2π}{3}\)
- Responder
-
\(\dfrac{π}{3}\), Cuadrante II,\( \sin \left(\dfrac{2π}{3}\right)=\dfrac{\sqrt{3}}{2}\),\( \cos \left(\dfrac{2π}{3}\right)=−\dfrac{1}{2}\)
48)\(\dfrac{5π}{6}\)
49)\(\dfrac{7π}{4}\)
- Responder
-
\(\dfrac{π}{4}\), Cuadrante IV,\( \sin \left(\dfrac{7π}{4}\right)=−\dfrac{\sqrt{2}}{2}\),\( \cos \left(\dfrac{7π}{4}\right)=\dfrac{\sqrt{2}}{2}\)
Para los ejercicios 50-59, encuentra el valor solicitado.
50) Si\(\cos (t)=\dfrac{1}{7}\) y\(t\) está en el\(4^{th}\) cuadrante, encuentra\( \sin (t)\).
51) Si\( \cos (t)=\dfrac{2}{9}\) y\(t\) está en el\(1^{st}\) cuadrante, encuentra\(\sin (t)\).
- Responder
-
\(\dfrac{\sqrt{77}}{9}\)
52) Si\(\sin (t)=\dfrac{3}{8}\) y\(t\) está en el\(2^{nd}\) cuadrante, encuentra\( \cos (t)\).
53) Si\( \sin (t)=−\dfrac{1}{4}\) y\(t\) está en el\(3^{rd}\) cuadrante, encuentra\(\cos (t)\).
- Responder
-
\(−\dfrac{\sqrt{15}}{4}\)
54) Encuentra las coordenadas del punto en un círculo con radio\(15\) correspondiente a un ángulo de\(220°\).
55) Encuentra las coordenadas del punto en un círculo con radio\(20\) correspondiente a un ángulo de\(120°\).
- Responder
-
\((−10,10\sqrt{3})\)
56) Encuentra las coordenadas del punto en un círculo con radio\(8\) correspondiente a un ángulo de\(\dfrac{7π}{4}\).
57) Encuentra las coordenadas del punto en un círculo con radio\(16\) correspondiente a un ángulo de\(\dfrac{5π}{9}\).
- Responder
-
\((–2.778,15.757)\)
58) Declarar el dominio de las funciones seno y coseno.
59) Indicar el rango de las funciones seno y coseno.
- Responder
-
\([–1,1]\)
Gráfica
Para los ejercicios 60-79, utilice el punto dado en el círculo unitario para encontrar el valor del seno y coseno de\(t\).
60)
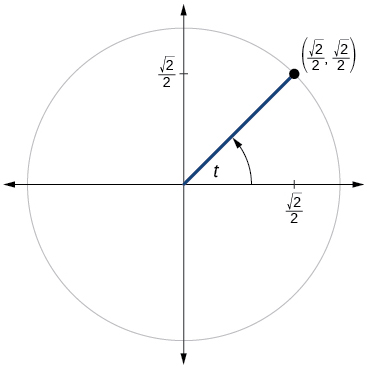
61)
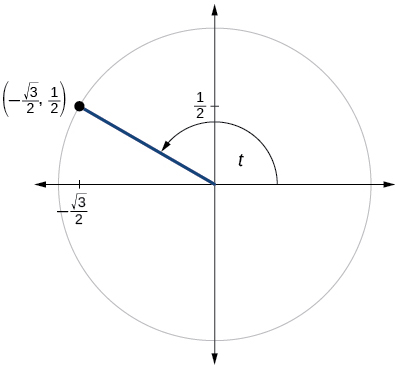
- Responder
-
\( \sin t=\dfrac{1}{2}, \cos t=−\dfrac{\sqrt{3}}{2}\)
62)
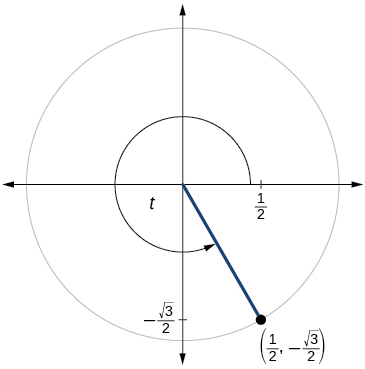
63)
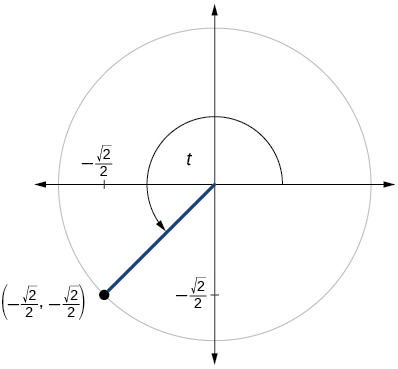
- Responder
-
\( \sin t=− \dfrac{\sqrt{2}}{2}, \cos t=−\dfrac{\sqrt{2}}{2}\)
64)
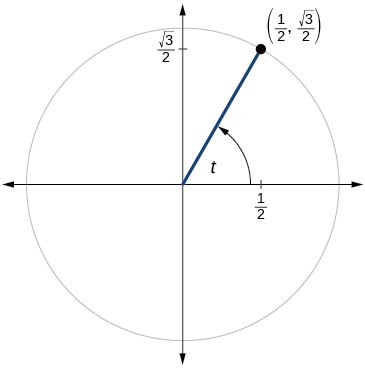
65)
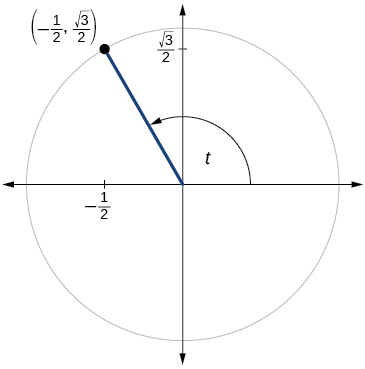
- Responder
-
\( \sin t=\dfrac{\sqrt{3}}{2},\cos t=−\dfrac{1}{2}\)
66)
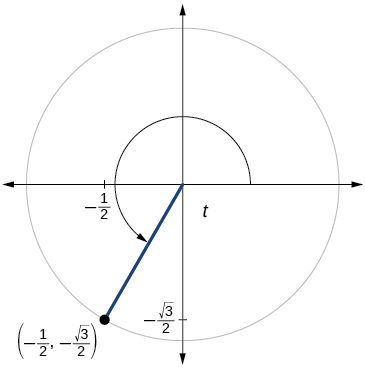
67)
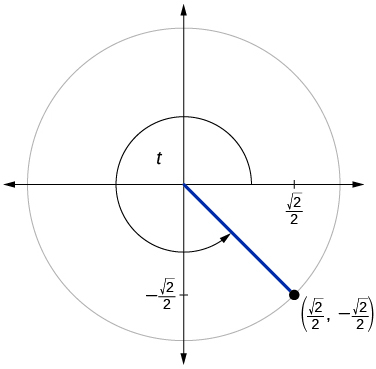
- Responder
-
\( \sin t=− \dfrac{\sqrt{2}}{2}, \cos t=\dfrac{\sqrt{2}}{2}\)
68)
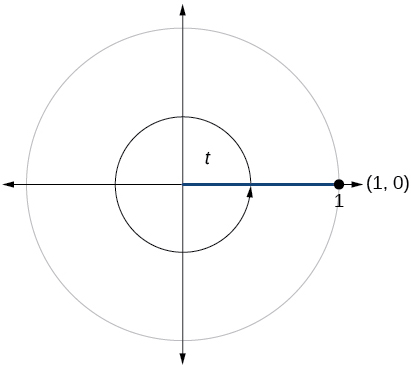
69)
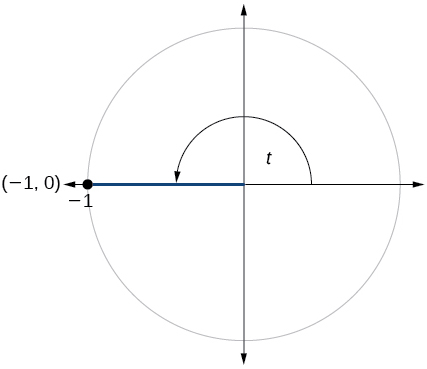
- Responder
-
\( \sin t=0, \cos t=−1\)
70)
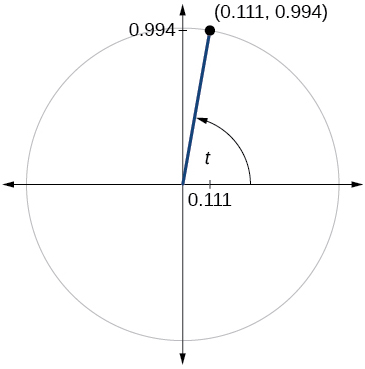
71)
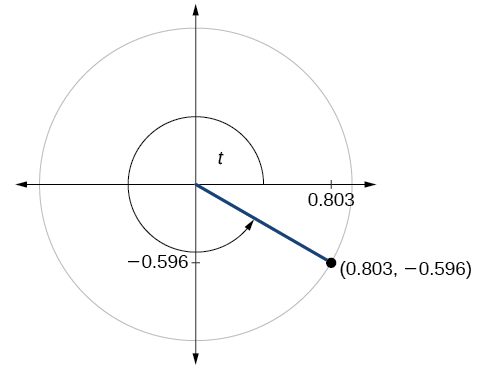
- Responder
-
\( \sin t=−0.596, \cos t=0.803\)
72)
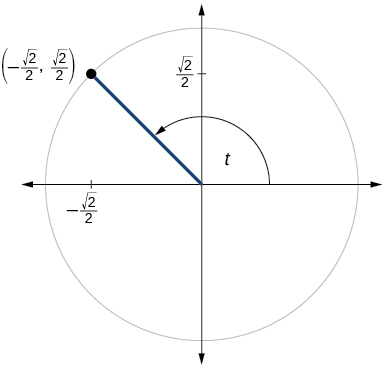
73)
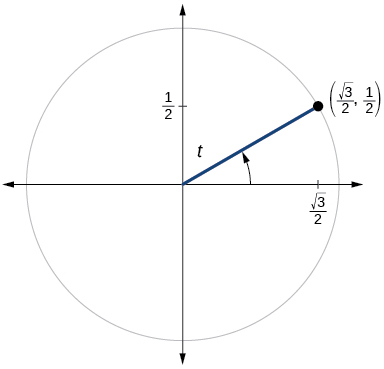
- Responder
-
\(\sin t=\dfrac{1}{2}, \cos t= \dfrac{\sqrt{3}}{2}\)
74)
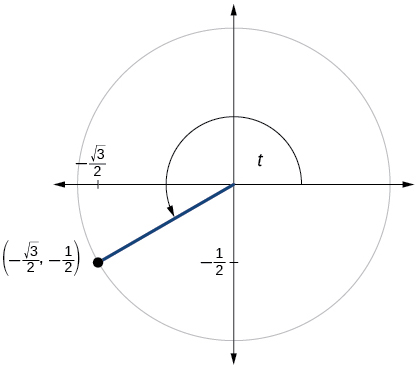
75)
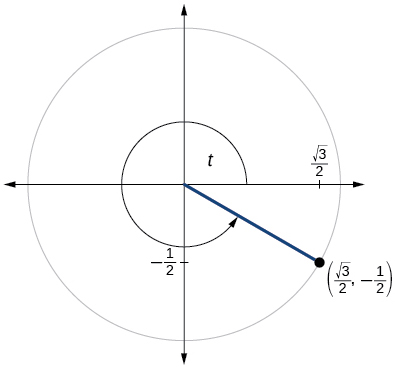
- Responder
-
\( \sin t=−\dfrac{1}{2}, \cos t= \dfrac{\sqrt{3}}{2} \)
76)
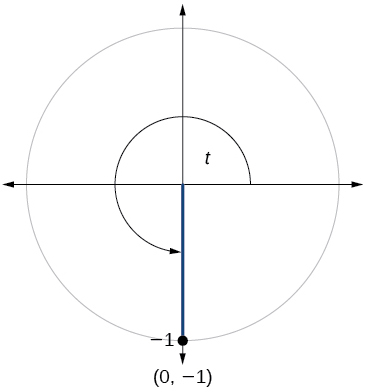
77)
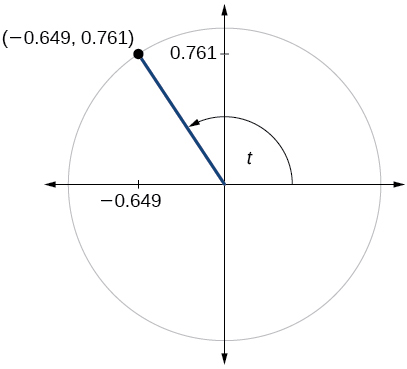
- Responder
-
\( \sin t=0.761, \cos t=−0.649 \)
78)
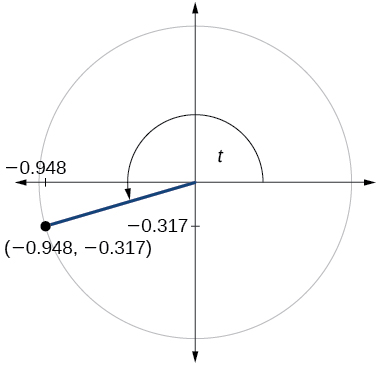
79)
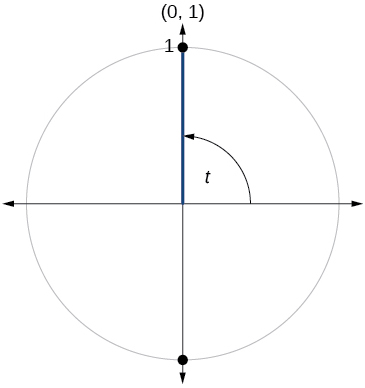
- Responder
-
\( \sin t=1, \cos t=0\)
Tecnología
Para los ejercicios 80-89, utilice una calculadora gráfica para evaluar.
80)\( \sin \dfrac{5π}{9}\)
81)\(cos \dfrac{5π}{9}\)
- Responder
-
\(−0.1736\)
82)\( \sin \dfrac{π}{10}\)
83)\( \cos \dfrac{π}{10}\)
- Responder
-
\(0.9511\)
84)\( \sin \dfrac{3π}{4}\)
85)\(\cos \dfrac{3π}{4}\)
- Responder
-
\(−0.7071\)
86)\( \sin 98° \)
87)\( \cos 98° \)
- Responder
-
\(−0.1392\)
88)\( \cos 310° \)
89)\( \sin 310° \)
- Responder
-
\(−0.7660\)
Extensiones
Para los ejercicios 90-99, evaluar.
90)\( \sin \left(\dfrac{11π}{3}\right) \cos \left(\dfrac{−5π}{6}\right)\)
91)\( \sin \left(\dfrac{3π}{4}\right) \cos \left(\dfrac{5π}{3}\right) \)
- Responder
-
\(\dfrac{\sqrt{2}}{4}\)
92)\( \sin \left(− \dfrac{4π}{3}\right) \cos \left(\dfrac{π}{2}\right)\)
93)\( \sin \left(\dfrac{−9π}{4}\right) \cos \left(\dfrac{−π}{6}\right)\)
- Responder
-
\(−\dfrac{\sqrt{6}}{4}\)
94)\( \sin \left(\dfrac{π}{6}\right) \cos \left(\dfrac{−π}{3}\right) \)
95)\( \sin \left(\dfrac{7π}{4}\right) \cos \left(\dfrac{−2π}{3}\right) \)
- Responder
-
\(\dfrac{\sqrt{2}}{4}\)
96)\( \cos \left(\dfrac{5π}{6}\right) \cos \left(\dfrac{2π}{3}\right)\)
97)\( \cos \left(\dfrac{−π}{3}\right) \cos \left(\dfrac{π}{4}\right) \)
- Responder
-
\(\dfrac{\sqrt{2}}{4}\)
98)\( \sin \left(\dfrac{−5π}{4}\right) \sin \left(\dfrac{11π}{6}\right)\)
99)\( \sin (π) \sin \left(\dfrac{π}{6}\right) \)
- Responder
-
\(0\)
Aplicaciones del mundo real
Para los ejercicios 100-104, usa este escenario: Un niño entra en un carrusel que tarda un minuto en girar una vez alrededor. El niño entra en el punto\((0,1)\), es decir, en la posición norte debida. Supongamos que el carrusel gira en sentido antihorario.
100) ¿Cuáles son las coordenadas del niño después de\(45\) segundos?
101) ¿Cuáles son las coordenadas del niño después de\(90\) segundos?
- Responder
-
\((0,–1)\)
102) ¿Cuáles son las coordenadas del niño después de\(125\) segundos?
103) ¿Cuándo tendrá coordenadas el niño\((0.707,–0.707)\) si el viaje dura\(6\) minutos? (Hay múltiples respuestas.)
- Responder
-
\(37.5\)segundos,\(97.5\) segundos,\(157.5\)\(217.5\) segundos,\(277.5\) segundos,\(337.5\) segundos
104) ¿Cuándo tendrá coordenadas el niño\((−0.866,−0.5)\) si el viaje dura\(6\) minutos?
5.3: Las Otras Funciones Trigonométricas
Verbal
1) En un intervalo de\([ 0,2π )\), ¿pueden ser iguales los valores de seno y coseno de un radián? Si es así, ¿dónde?
- Responder
-
Sí, cuando el ángulo de referencia es\(\dfrac{π}{4}\) y el lado terminal del ángulo está en los cuadrantes I y III. Así, at\(x=\dfrac{π}{4},\dfrac{5π}{4}\), los valores de seno y coseno son iguales.
2) ¿Cuál estimaría que sería el coseno de\(\pi \) grados? Explica tu razonamiento.
3) Para cualquier ángulo en el cuadrante II, si conocías el seno del ángulo, ¿cómo podrías determinar el coseno del ángulo?
- Responder
-
Sustituir el seno del ángulo en por\(y\) en el Teorema de Pitágoras\(x^2+y^2=1\). Resuelve\(x\) y toma la solución negativa.
4) Describir la función secante.
5) Tangente y cotangente tienen un periodo de\(π\). ¿Qué nos dice esto sobre la salida de estas funciones?
- Responder
-
Las salidas de tangente y cotangente repetirán cada\(π\) unidad.
Algebraico
Para los ejercicios 6-17, encuentra el valor exacto de cada expresión.
6)\( \tan \dfrac{π}{6}\)
7)\(\sec \dfrac{π}{6}\)
- Responder
-
\(\dfrac{2\sqrt{3}}{3}\)
8)\( \csc \dfrac{π}{6}\)
9)\( \cot \dfrac{π}{6}\)
- Responder
-
\(\sqrt{3}\)
10)\( \tan \dfrac{π}{4}\)
11)\( \sec \dfrac{π}{4}\)
- Responder
-
\(\sqrt{2}\)
12)\( \csc \dfrac{π}{4}\)
13)\( \cot \dfrac{π}{4}\)
- Responder
-
\(1\)
14)\( \tan \dfrac{π}{3}\)
15)\( \sec \dfrac{π}{3}\)
- Responder
-
\(2\)
16)\( \csc \dfrac{π}{3}\)
17)\( \cot \dfrac{π}{3}\)
- Responder
-
\(\dfrac{\sqrt{3}}{3}\)
Para los ejercicios 18-48, utilice ángulos de referencia para evaluar la expresión.
18)\( \tan \dfrac{5π}{6}\)
19)\( \sec \dfrac{7π}{6}\)
- Responder
-
\(−\dfrac{2\sqrt{3}}{3}\)
20)\( \csc \dfrac{11π}{6}\)
21)\( \cot \dfrac{13π}{6}\)
- Responder
-
\(\sqrt{3}\)
22)\( \tan \dfrac{7π}{4}\)
23)\( \sec \dfrac{3π}{4}\)
- Responder
-
\(−\sqrt{2}\)
24)\( \csc \dfrac{5π}{4}\)
25)\( \cot \dfrac{11π}{4}\)
- Responder
-
\(−1\)
26)\( \tan \dfrac{8π}{3}\)
27)\( \sec \dfrac{4π}{3}\)
- Responder
-
\(−2\)
28)\( \csc \dfrac{2π}{3}\)
29)\( \cot \dfrac{5π}{3}\)
- Responder
-
\(−\dfrac{\sqrt{3}}{3}\)
30)\( \tan 225°\)
31)\( \sec 300°\)
- Responder
-
\(2\)
32)\( \csc 150°\)
33)\( \cot 240°\)
- Responder
-
\(\dfrac{\sqrt{3}}{3}\)
34)\( \tan 330°\)
35)\( \sec 120°\)
- Responder
-
\(−2\)
36)\( \csc 210°\)
37)\( \cot 315°\)
- Responder
-
\(−1\)
38) Si\( \sin t= \dfrac{3}{4}\), y\(t\) está en el cuadrante II, encuentra\( \cos t, \sec t, \csc t, \tan t, \cot t \).
39) Si\( \cos t=−\dfrac{1}{3},\) y\(t\) está en el cuadrante III, encuentra\( \sin t, \sec t, \csc t, \tan t, \cot t\).
- Responder
-
Si\(\sin t=−\dfrac{2\sqrt{2}}{3}, \sec t=−3, \csc t=−\csc t=−\dfrac{3\sqrt{2}}{4},\tan t=2\sqrt{2}, \cot t= \dfrac{\sqrt{2}}{4}\)
40) Si\(\tan t=\dfrac{12}{5},\) y\(0≤t< \dfrac{π}{2}\), encontrar\( \sin t, \cos t, \sec t, \csc t,\) y\(\cot t\).
41) Si\( \sin t= \dfrac{\sqrt{3}}{2}\) y\( \cos t=\dfrac{1}{2},\) encontrar\( \sec t, \csc t, \tan t,\) y\( \cot t\).
- Responder
-
\( \sec t=2, \csc t=\csc t=\dfrac{2\sqrt{3}}{3}, \tan t= \sqrt{3}, \cot t= \dfrac{\sqrt{3}}{3}\)
42) Si\( \sin 40°≈0.643 \; \cos 40°≈0.766 \; \sec 40°,\csc 40°,\tan 40°, \text{ and } \cot 40°\).
43) Si\( \sin t= \dfrac{\sqrt{2}}{2},\) ¿cuál es el\( \sin (−t)\)?
- Responder
-
\(−\dfrac{\sqrt{2}}{2}\)
44) Si\( \cos t= \dfrac{1}{2},\) ¿cuál es el\( \cos (−t)\)?
45) Si\( \sec t=3.1,\) ¿cuál es el\( \sec (−t)\)?
- Responder
-
\(3.1\)
46) Si\( \csc t=0.34,\) ¿cuál es el\( \csc (−t)\)?
47) Si\( \tan t=−1.4,\) ¿cuál es el\( \tan (−t)\)?
- Responder
-
\(1.4\)
48) Si\( \cot t=9.23,\) ¿cuál es el\( \cot (−t)\)?
Gráfica
Para los ejercicios 49-51, utilice el ángulo en el círculo unitario para encontrar el valor de cada una de las seis funciones trigonométricas.
49)
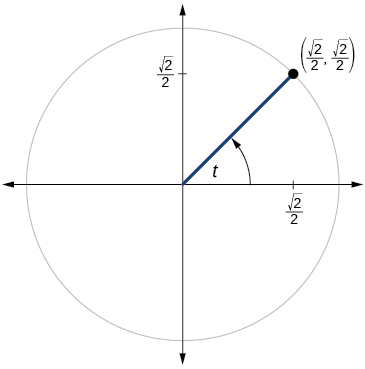
- Responder
-
\( \sin t= \dfrac{\sqrt{2}}{2}, \cos t= \dfrac{\sqrt{2}}{2}, \tan t=1,\cot t=1,\sec t= \sqrt{2}, \csc t= \csc t= \sqrt{2} \)
50)
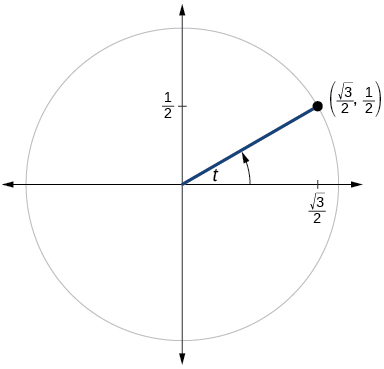
51)
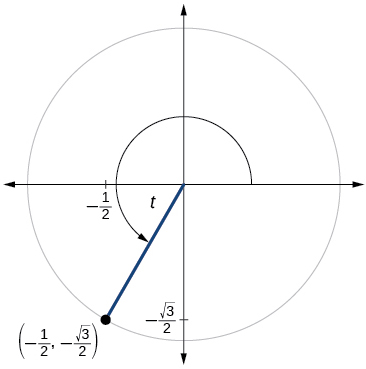
- Responder
-
\( \sin t=−\dfrac{\sqrt{3}}{2}, \cos t=−\dfrac{1}{2}, \tan t=\sqrt{3}, \cot t= \dfrac{\sqrt{3}}{3}, \sec t=−2, \csc t=−\csc t=−\dfrac{2\sqrt{3}}{3} \)
Tecnología
Para los ejercicios 52-61, utilice una calculadora gráfica para evaluar.
52)\( \csc \dfrac{5π}{9}\)
53)\( \cot \dfrac{4π}{7}\)
- Responder
-
\(–0.228\)
54)\( \sec \dfrac{π}{10}\)
55)\( \tan \dfrac{5π}{8}\)
- Responder
-
\(–2.414\)
56)\( \sec \dfrac{3π}{4}\)
57)\( \csc \dfrac{π}{4}\)
- Responder
-
\(1.414\)
58)\( \tan 98°\)
59)\( \cot 33°\)
- Responder
-
\(1.540\)
60)\( \cot 140°\)
61)\( \sec 310° \)
- Responder
-
\(1.556\)
Extensiones
Para los ejercicios 62-69, utilizar identidades para evaluar la expresión.
62) Si\(\tan (t)≈2.7,\) y\( \sin (t)≈0.94,\) encuentra\( \cos (t)\).
63) Si\( \tan (t)≈1.3,\) y\( \cos (t)≈0.61\), encuentra\( \sin (t)\).
- Responder
-
\( \sin (t)≈0.79 \)
64) Si\( \csc (t)≈3.2,\) y\( \csc (t)≈3.2,\) y\( \cos (t)≈0.95,\) encontrar\( \tan (t)\).
65) Si\( \cot (t)≈0.58,\) y\( \cos (t)≈0.5,\) encuentra\( \csc (t)\).
- Responder
-
\( \csc (t)≈1.16\)
66) Determinar si la función\(f(x)=2 \sin x \cos x\) es par, impar o ninguna.
67) Determinar si la función\(f(x)=3 \sin ^2 x \cos x + \sec x\) es par, impar o ninguna.
- Responder
-
incluso
68) Determinar si la función\(f(x)= \sin x −2 \cos ^2 x \) es par, impar o ninguna.
69) Determinar si la función\(f(x)= \csc ^2 x+ \sec x\) es par, impar o ninguna.
- Responder
-
incluso
Para los ejercicios 70-71, utilizar identidades para simplificar la expresión.
70)\( \csc t \tan t\)
71)\( \dfrac{\sec t}{ \csc t}\)
- Responder
-
\( \dfrac{ \sin t}{ \cos t}= \tan t\)
Aplicaciones del mundo real
72) La cantidad de luz solar en una ciudad determinada puede ser modelada por la función\(h=15 \cos \left(\dfrac{1}{600}d\right),\) donde\(h\) representa las horas de luz solar, y\(d\) es el día del año. Usa la ecuación para encontrar cuántas horas de luz solar hay el 10 de febrero,\(42^{nd}\) día del año. Indicar el periodo de la función.
73) La cantidad de luz solar en una ciudad determinada puede ser modelada por la función\(h=16 \cos \left(\dfrac{1}{500}d\right)\), donde\(h\) representa las horas de luz solar, y\(d\) es el día del año. Usa la ecuación para encontrar cuántas horas de luz solar hay el 24 de septiembre,\(267^{th}\) día del año. Indicar el periodo de la función.
- Responder
-
\(13.77\)horas, periodo:\(1000π\)
74) La ecuación\(P=20 \sin (2πt)+100\) modela la presión arterial\(P\), donde\(t\) representa el tiempo en segundos.
- Encuentra la presión arterial después de\(15\) segundos.
- ¿Cuáles son las presiones sanguíneas máxima y mínima?
75) La altura de un pistón\(h\), en pulgadas, puede ser modelada por la ecuación\(y=2 \cos x+6,\) donde\(x\) representa el ángulo del cigüeñal. Encuentra la altura del pistón cuando el ángulo del cigüeñal es\(55°\).
- Responder
-
\(7.73\)pulgadas
76) La altura de un pistón\(h\), en pulgadas, puede ser modelada por la ecuación\(y=2 \cos x+5,\) donde\(x\) representa el ángulo del cigüeñal. Encuentra la altura del pistón cuando el ángulo del cigüeñal es\(55°\).
5.4: Trigonometría de Triángulo Recto
Verbal
1) Para el triángulo rectángulo dado, etiquetar el lado adyacente, el lado opuesto y la hipotenusa para el ángulo indicado.
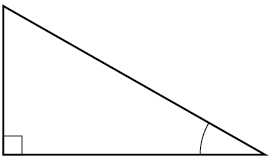
- Contestar
-
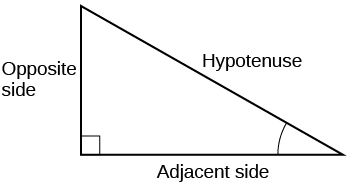
2) Cuando se coloca un triángulo rectángulo con\(1\) hipotenusa de en el círculo unitario, ¿qué lados del triángulo corresponden a las\(y\) coordenadas\(x\) - y -?
3) ¿La tangente de un ángulo compara qué lados del triángulo rectángulo?
- Contestar
-
La tangente de un ángulo es la relación del lado opuesto al lado adyacente.
4) ¿Cuál es la relación entre los dos ángulos agudos en un triángulo rectángulo?
5) Explicar la identidad de la cofunción.
- Contestar
-
Por ejemplo, el seno de un ángulo es igual al coseno de su complemento; el coseno de un ángulo es igual al seno de su complemento.
Algebraico
Para los ejercicios 6-9, utilizar cofunciones de ángulos complementarios.
6)\( \cos (34°)= \sin (\_\_°)\)
7)\( \cos (\dfrac{π}{3})= \sin (\_\_\_) \)
- Contestar
-
\(\dfrac{π}{6}\)
8)\( \csc (21°) = \sec (\_\_\_°)\)
9)\( \tan (\dfrac{π}{4})= \cot (\_\_)\)
- Contestar
-
\(\dfrac{π}{4}\)
Para los ejercicios 10-16, encuentra las longitudes de los lados faltantes si lado\(a\) es ángulo opuesto\(A\), lado\(b\) es ángulo opuesto\(B\), y lado\(c\) es la hipotenusa.
10)\( \cos B= \dfrac{4}{5},a=10\)
11)\( \sin B= \dfrac{1}{2}, a=20\)
- Contestar
-
\(b= \dfrac{20\sqrt{3}}{3},c= \dfrac{40\sqrt{3}}{3}\)
12)\( \tan A= \dfrac{5}{12},b=6\)
13)\( \tan A=100,b=100\)
- Contestar
-
\(a=10,000,c=10,000.5\)
14)\(\sin B=\dfrac{1}{\sqrt{3}}, a=2 \)
15)\(a=5, ∡ A=60^∘\)
- Contestar
-
\(b=\dfrac{5\sqrt{3}}{3},c=\dfrac{10\sqrt{3}}{3}\)
16)\(c=12, ∡ A=45^∘\)
Gráfica
Para los ejercicios 17-22, use la Figura a continuación para evaluar cada función trigonométrica del ángulo\(A\).
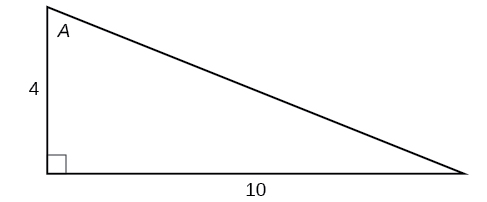
17)\(\sin A\)
- Contestar
-
\(\dfrac{5\sqrt{29}}{29}\)
18)\( \cos A \)
19)\( \tan A \)
- Contestar
-
\(\dfrac{5}{2}\)
20)\(\csc A \)
21)\( \sec A \)
- Contestar
-
\(\dfrac{\sqrt{29}}{2}\)
22)\( \cot A \)
Para los ejercicios 23-,28 usa la Figura a continuación para evaluar cada función trigonométrica del ángulo\(A\).
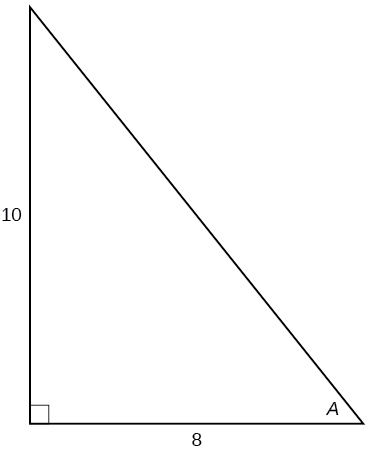
23)\( \sin A\)
- Contestar
-
\(\dfrac{5\sqrt{41}}{41}\)
24)\( \cos A\)
25)\( \tan A \)
- Contestar
-
\(\dfrac{5}{4}\)
26)\( \csc A\)
27)\( \sec A\)
- Contestar
-
\(\dfrac{\sqrt{41}}{4}\)
28)\(\cot A\)
Para los ejercicios 29-31, resolver por los lados desconocidos del triángulo dado.
29)
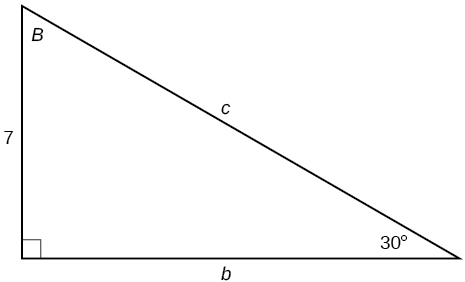
- Contestar
-
\(c=14, b=7\sqrt{3}\)
30)
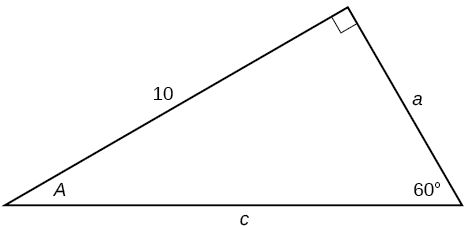
31)
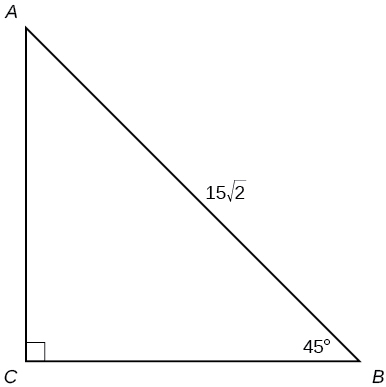
- Contestar
-
\(a=15, b=15 \)
Tecnología
Para los ejercicios 32-41, usa una calculadora para encontrar la longitud de cada lado a cuatro decimales.
32)
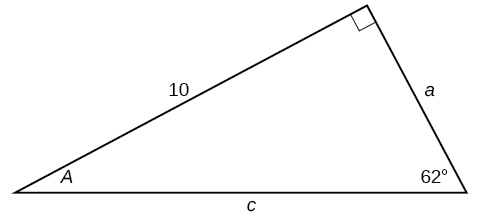
33)
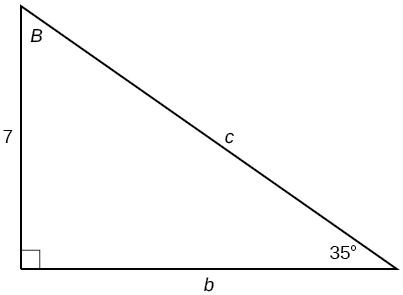
- Contestar
-
\(b=9.9970, c=12.2041\)
34)
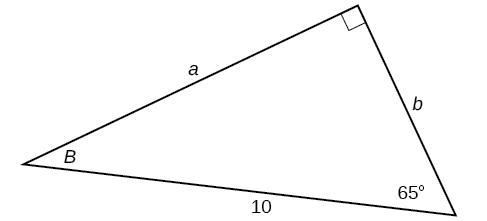
35)
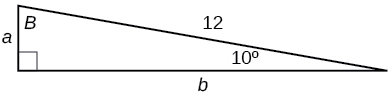
- Contestar
-
\(a=2.0838, b=11.8177\)
36)
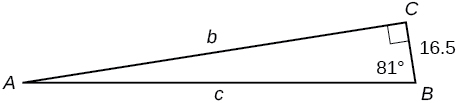
37)\(b=15, ∡B=15^∘\)
- Contestar
-
\(a=55.9808,c=57.9555\)
38)\(c=200, ∡B=5^∘\)
39)\(c=50, ∡B=21^∘\)
- Contestar
-
\(a=46.6790,b=17.9184\)
40)\(a=30, ∡A=27^∘\)
41)\(b=3.5, ∡A=78^∘\)
- Contestar
-
\(a=16.4662,c=16.8341\)
Extensiones
42) Encontrar\(x\).
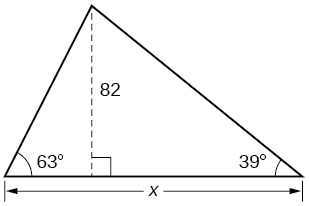
43) Encontrar\(x\).
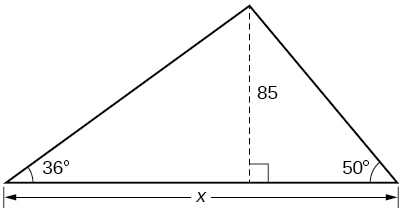
- Contestar
-
\(188.3159\)
44) Encontrar\(x\).
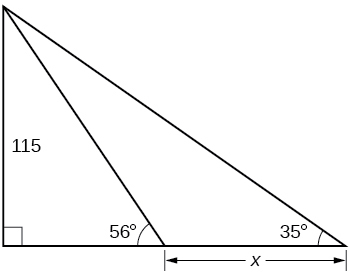
45) Encontrar\(x\).
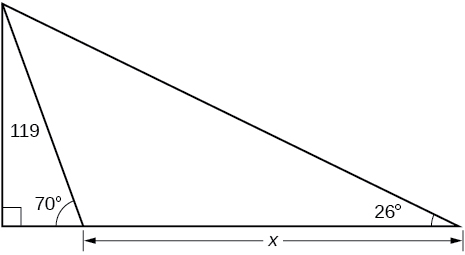
- Contestar
-
\(200.6737\)
46) Una torre de radio se encuentra a\(400\) pies de un edificio. Desde una ventana en el edificio, una persona determina que el ángulo de elevación a la parte superior de la torre es\(36°\), y que el ángulo de depresión al fondo de la torre es\(23°\). ¿Qué tan alta es la torre?
47) Una torre de radio se encuentra a\(325\) pies de un edificio. Desde una ventana en el edificio, una persona determina que el ángulo de elevación a la parte superior de la torre es\(43°\), y que el ángulo de depresión al fondo de la torre es\(31°\). ¿Qué tan alta es la torre?
- Contestar
-
\(498.3471\)ft
48) A lo lejos se encuentra un monumento de un\(200\) pie de altura. Desde una ventana en un edificio, una persona determina que el ángulo de elevación a la parte superior del monumento es\(15°\), y que el ángulo de depresión al fondo de la torre es\(2°\). ¿A qué distancia está la persona del monumento?
49) A lo lejos se encuentra un monumento de un\(400\) pie de altura. Desde una ventana en un edificio, una persona determina que el ángulo de elevación a la parte superior del monumento es\(18°\), y que el ángulo de depresión al fondo del monumento es\(3°\). ¿A qué distancia está la persona del monumento?
- Contestar
-
\(1060.09\)ft
50) Hay una antena en la parte superior de un edificio. Desde una ubicación a\(300\) pies de la base del edificio, el ángulo de elevación hasta la parte superior del edificio se mide para ser\(40°\). Desde la misma ubicación, el ángulo de elevación a la parte superior de la antena se mide para ser\(43°\). Encuentra la altura de la antena.
51) Hay pararrayos en la parte superior de un edificio. Desde una ubicación a\(500\) pies de la base del edificio, el ángulo de elevación hasta la parte superior del edificio se mide para ser\(36°\). Desde la misma ubicación, el ángulo de elevación a la parte superior del pararrayos se mide para ser\(38°\). Encuentra la altura del pararrayos.
- Contestar
-
\(27.372\)ft
Aplicaciones del mundo real
52) Una escalera\(33\) de pies se apoya contra un edificio para que el ángulo entre el suelo y la escalera sea\(80°\). ¿Qué tan alto llega la escalera hasta el costado del edificio?
53) Una escalera\(23\) de pies se apoya contra un edificio para que el ángulo entre el suelo y la escalera sea\(80°\). ¿Qué tan alto llega la escalera hasta el costado del edificio?
- Contestar
-
\(22.6506\)ft
54) El ángulo de elevación a la parte superior de un edificio en Nueva York se encuentra a\(9\) grados del suelo a una distancia de\(1\) milla de la base del edificio. Usando esta información, encuentra la altura del edificio.
55) El ángulo de elevación a la parte superior de un edificio en Seattle se encuentra a\(2\) grados del suelo a una distancia de\(2\) millas de la base del edificio. Usando esta información, encuentra la altura del edificio.
- Contestar
-
\(368.7633\)ft
56) Suponiendo que una secoya gigante de\(370\) -pie de altura crece verticalmente, si camino cierta distancia del árbol y mido el ángulo de elevación a la parte superior del árbol para estar\(60°\), ¿qué tan lejos de la base del árbol estoy?


