1.4: Desigualdades de valor absoluto

Última actualización
Guardar como PDF

Page ID: 117755

Thomas Tradler and Holly Carley
CUNY New York City College of Technology via New York City College of Technology at CUNY Academic Works

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Usando la notación de la sección anterior, ahora resolvemos desigualdades que involucran el valor absoluto. Estas desigualdades pueden resolverse en tres pasos:

Paso 1: Resolver la igualdad correspondiente. La solución de la igualdad divide la línea numérica real en varios subintervalos.
Paso 2: Usando el paso 1, verifique la desigualdad para un número en cada uno de los subintervalos. Esta comprobación determina los intervalos del conjunto de soluciones.
Paso 3: Verifique los puntos finales de los intervalos.

Aquí hay algunos ejemplos para el método de solución anterior.

Ejemplo$\PageIndex{1}$

Resolver para$x$:

$|x+7|<2$
$|3x-5|\geq 11$
$|12-5x|\leq 1$

Solución

Seguimos los tres pasos descritos anteriormente. En el paso 1, resolvemos la igualdad correspondiente,$|x+7|=2$. $x+7=2$&$x+7=-2$ \[\begin{array}{l|l}
x+7=2 & x+7=-2 \\
\Longrightarrow x=-5 & \Longrightarrow x=-9
\end{array} \nonumber \] Las soluciones$x=-5$ y$x=-9$ dividir la línea numérica en tres subintervalos:

Ahora, en el paso 2, comprobamos la desigualdad para un número en cada uno de estos subintervalos.

\ [\ begin {array} {c|c|c}
\ text {Comprobar:}\ quad x=-10 &\ text {Comprobar:}\ quad x=-7 &\ text {Comprobar:}\ quad x=0\
| (-10) +7|\ stackrel {?} {<} 2 & | (-7) +7|\ stackrel {?} {<} 2 & |0+7|\ stackrel {?} {<} 2\\
|-3|\ stackrel {?} {<} 2 & |0|\ stackrel {?} {<} 2 & |7|\ stackrel {?} {<} 2\\
3\ stackrel {?} {<} 2 & 0\ stackrel {?} {<} 2 y 7\ stackrel {?} {<} 2\\
\ text {false} &\ text {true} &\ text {false}
\ end {array}\ nonumber\]

Ya que$x=-7$ en el subintervalo dado por$-9<x<-5$ resuelve la desigualdad$|x+7|<2$, se deduce que todos los números en el subintervalo dado por$-9<x<-5$ resuelven la desigualdad. De igual manera, dado que$x=-10$ y$x=0$ no resuelven la desigualdad, ningún número en estos subintervalos resolverá la desigualdad. Para el paso 3, observamos que los números$x=-9$ y no$x=-5$ se incluyen como soluciones ya que la desigualdad es estricta (es decir, tenemos$<$ en lugar de$\leq$) .El conjunto de soluciones es por lo tanto el intervalo$S=(-9,-5)$. La solución en la línea numérica es:

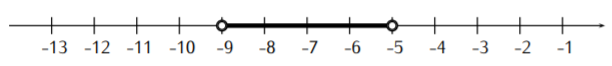
$clipboard_ea1d81614b0d8e2564fd8ec56ba182dbf.png$

Seguimos los pasos como antes. Primero, en el paso 1, resolvemos$|3x-5|=11$. \ [\ begin {array} {l|l}
3 x-5=11 y 3 x-5=-11\\
\ Longrightarrow 3 x=16 &\ Longrightarrow 3 x=-6\\
\ LongRightarrow x=\ dfrac {16} {3} &\ RightRightarrow x=-2
\ end {array}\ nonumber\]

Las dos soluciones$x=-2$ y$x=\dfrac{16}{3}=5\dfrac {1}{3}$ dividir la línea numérica en los subintervalos que se muestran a continuación. \[x<-2 \hspace{1in} -2<x<5\frac 1 3 \hspace{1in} 5\frac 1 3<x \nonumber\]

$clipboard_e0d7878e0eca72b0ee120cafa8166dd75.png$

Para el paso 2, verificamos un número en cada subintervalo. Esto da:

\ [\ begin {array} {c|c|c|c}
\ text {Comprobar:} x=-3 &\ text {Comprobar:}\ quad x=1 &\ text {Comprobar:}\ quad x=6\\
|3\ cdot (-3) -5|\ stackrel {?} {\ geq} 11 & |3\ cdot 1-5|\ stackrel {?} {\ geq} 11 & |3\ cdot 6-5|\ stackrel {?} {\ geq} 11\\
|-9-5|\ stackrel {?} {\ geq} 11 & |3-5|\ stackrel {?} {\ geq} 11 & |18-5|\ stackrel {?} {\ geq} 11\\
|-14|\ stackrel {?} {\ geq} 11 & |-2|\ stackrel {?} {\ geq} 11 & |13|\ stackrel {?} {\ geq} 11\\
14\ stackrel {?} {\ geq} 11 y 2\ stackrel {?} {\ geq} 11 y 13\ stackrel {?} {\ geq} 11\\
\ text {true} &\ text {false} &\ text {true}
\ end {array}\ nonumber\]

Para el paso 3, tenga en cuenta que incluimos$-2$ y$5\dfrac {1}{3}$ en el conjunto de soluciones ya que la desigualdad es “mayor o igual a” (es decir$\geq$, a diferencia de$>$). Además, los números$-\infty$ y no$\infty$ están incluidos, ya que no$\pm\infty$ son números reales.

El conjunto de soluciones es, por lo tanto, la unión de los dos intervalos:\[S=\Big(-\infty,-2\Big]\cup \Big[5\dfrac {1}{3}, \infty\Big) \nonumber \]

Para resolver$|12-5x|\leq 1$, primero resolvemos la igualdad$|12-5x|=1$. \ [\ begin {array} {l|l}
12-5 x=1 & 12-5 x=-1\
\ Longrightarrow-5 x=-11 &\ Longrightarrow x=-13\
\ LongRightarrow x=\ frac {-11} {-5} =2.2 &\ LongRightarrow x=\ frac {-13} {-5} =2.6
\ end {array}\ nonumber\]

Esto divide la recta numérica en tres subintervalos, y verificamos la desigualdad original$|12-5x|\leq 1$ para un número en cada uno de estos subintervalos.

\ [\ begin {array} {c|c|c|c}
\ text {Intervalo:}\ quad x<2.2 &\ text {Intervalo:}\ quad 2.2<x<2.6 &\ text {Intervalo:}\ quad 2.6<x
\\ texto {Comprobación:}\ quad x=1 &\ text {Comprobación:}\ quad x=2.4 &\ texto {Comprobación:}\ quad x=3\
|12-5\ cdot 1|\ stackrel { ?} {\ leq} 1 & |12-5\ cdot 1|\ stackrel {?} {\ leq} 1 & |12-5\ cdot 3|\ stackrel {?} {\ leq} 1\\
|12-5|\ stackrel {?} {\ leq} 1 & |12-12|\ stackrel {?} {\ leq} 1 & |12-15|\ stackrel {?} {\ leq} 1\\
|7|\ stackrel {?} {\ leq} 1 & |0|\ stackrel {?} {\ leq} 1 & |-3|\ stackrel {?} {\ leq} 1\\
7\ stackrel {?} {\ leq} 1 & 0\ stackrel {?} {\ leq} 1 y 3\ stackrel {?} {\ leq} 1\\
\ text {false} &\ text {true} &\ text {false}
\ end {array}\ nonumber\]

El conjunto de soluciones es el intervalo$S=[2.2,2.6]$, donde incluimos$x=2.2$ y$x=2.6$ ya que la desigualdad original “menor o igual a” ($\leq$) incluye la igualdad.

Nota

Alternativamente, siempre que tengas una desigualdad de valor absoluta puedes convertirla en dos desigualdades.

Aquí hay un par de ejemplos.

Ejemplo$\PageIndex{2}$

Resolver para$x$:$|12-5x|\leq 1$

Solución

Tenga en cuenta que$|12-5x|\leq 1$ implica que

\[-1\leq 12-5x\leq1 \nonumber \]

para que

\[-13\leq -5x\leq -11 \nonumber \]

y dividiendo por$-5$ (recordando cambiar la dirección de las desigualdades al multiplicar o dividir por un número negativo) vemos que

\[\frac{13}{5}\geq x\geq \frac{11}{5} \nonumber \]

o en notación de intervalos, tenemos el conjunto de soluciones

\[S=\left[\frac{11}{5},\frac{13}{5}\right] \nonumber\]

Ejemplo$\PageIndex{3}$

Si$|x+6|>2$ entonces cualquiera$x+6>2$ o$x+6<-2$ así que cualquiera$x>-4$ o$x<-8$ así que en notación de intervalos la solución es$S=(-\infty,-8)\cup(-4,\infty)$.

Solución

Hay una interpretación geométrica del valor absoluto en la recta numérica como la distancia entre dos números:

$clipboard_e8a95ea5bc21fc953df9681bc64a8644c.png$

distancia entre$a$ y$b$ es$|b-a|$ que también es igual a$|a-b|$

Esta interpretación también puede ser utilizada para resolver ecuaciones de valores absolutos y desigualdades.

Ejemplo$\PageIndex{4}$

Resolver para$x$:

$|x-6|=4$
$|x-6|\leq 4$
$|x-6|\geq 4$

Solución

Considere la distancia entre$x$ y$6$ para estar$4$ en una recta numérica:

$clipboard_e17c977283e3ff391111c7da91e948997.png$

Hay dos soluciones,$x=2$ o$x=10$. Es decir, la distancia entre$2$ y$6$ es$4$ y la distancia entre$10$ y$6$ es$4$.

Los números dentro de las llaves de arriba tienen distancia$4$ o menos. La solución se da en la línea numérica como:

$clipboard_e54e786ef1671d92c3b9291ecb0fc38f1.png$

En notación de intervalos, el conjunto de soluciones es el intervalo$S=[2,10]$. También se puede escribir que el conjunto de soluciones consiste en todos$x$ tales que$2\leq x\leq 10$.

Los números fuera de las llaves anteriores tienen distancia$4$ o más. La solución se da en la línea numérica como:

$clipboard_ea020fa310cf3fcba8ba44ff547e18ed9.png$

En notación de intervalos, el conjunto de soluciones es el intervalo$(-\infty,2]$ y$[10,\infty)$, o en definitiva, es la unión de los dos intervalos:

\[S= (\infty,2]\cup [10,\infty) \nonumber \]

También se puede escribir que el conjunto de soluciones consiste en todos$x$ tales que$x\leq 2$ o$x\geq 10$.

Ejemplo\(\PageIndex{1}\)

Nota

Ejemplo\(\PageIndex{2}\)

Ejemplo\(\PageIndex{3}\)

Ejemplo\(\PageIndex{4}\)