3.2: Funciones dadas por las gráficas

Última actualización
Guardar como PDF

Page ID: 117717

Thomas Tradler and Holly Carley
CUNY New York City College of Technology via New York City College of Technology at CUNY Academic Works

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

En muchas situaciones, una función es representada por su gráfica. La gráfica de una función$f$ es el conjunto de todos los puntos (en el plano de coordenadas) de la forma$(x,f(x))$, donde$x$ está en el dominio de$f$. Ya hemos visto un ejemplo de graficar una función cuando discutimos líneas y sus gráficas. Aquí hay otro ejemplo que muestra cómo la definición formulaica se relaciona con la gráfica de la función.

Ejemplo$\PageIndex{1}$

Dejemos$y=x^2$ con dominio$D=\mathbb{R}$ siendo el conjunto de todos los números reales. Podemos graficar esto después de calcular una tabla de la siguiente manera:

\ [\ begin {array} {|c||c|c|c|c|c|c|c|c|}
\ hline x & -3 & -2 & -1 & 0 & 1 & 2 & 3\
\ hline\ hline\ hline y & 9 & 4 & 1 & 0 & 1 & 4 & 9\
\ hline
\ end {array}\ nonumber\]

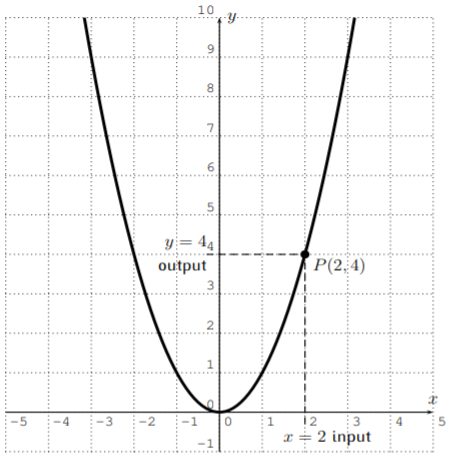
$clipboard_e7b2d8c660208c644ef2e1fe8df1f1bfe.png$

Muchos valores de función se pueden leer de esta gráfica. Por ejemplo, para la entrada$x=2$, obtenemos la salida$y=4$. Esto corresponde al punto$P(2,4)$ en la gráfica como se representa anteriormente.

En general, una entrada (colocada en el$x$ eje -axis) se asigna a una salida (colocada en el$y$ eje -) según donde la línea vertical en se$x$ intersecta con la gráfica dada. Esto se usa en el siguiente ejemplo.

Ejemplo$\PageIndex{2}$

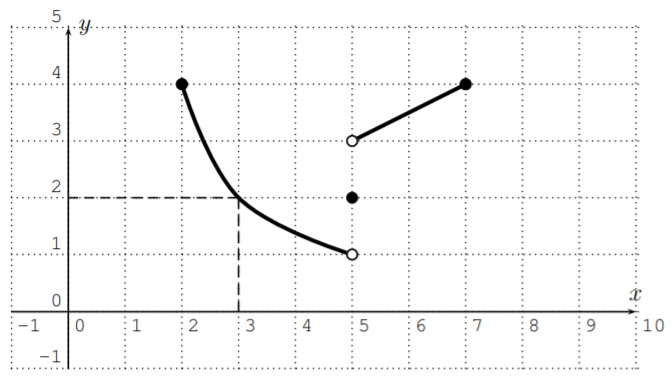
Dejar$f$ ser la función dada por la siguiente gráfica. Encuentra el dominio y la gama de$f$.

$clipboard_ebe00de41800f4c0d6c3d23cbf1981655.png$

Solución

Aquí, las líneas discontinuas muestran, que la entrada$x=3$ da una salida de$y=2$. Del mismo modo, podemos obtener otros valores de salida de la gráfica:

\[f(2)=4, \quad f(3)=2, \quad f(5)=2, \quad f(7)=4 \nonumber \]

Tenga en cuenta que en la gráfica anterior, un punto cerrado significa que el punto es parte de la gráfica, mientras que un punto abierto significa que no es parte de la gráfica.

El dominio es el conjunto de todos los valores de entrada posibles en el$x$ eje -axis. Como podemos tomar cualquier número$2\leq x \leq7$ como entrada, el dominio es el intervalo$D=[2,7]$.

El rango es el conjunto de todos los valores de salida posibles en el$y$ eje -axis. Dado que cualquier número$1<y\leq 4$ se obtiene como salida, el rango es$R=(1,4]$. Obsérvese en particular, que no$y=1$ es una salida, ya que$f(5)=2$.

Ejemplo$\PageIndex{3}$

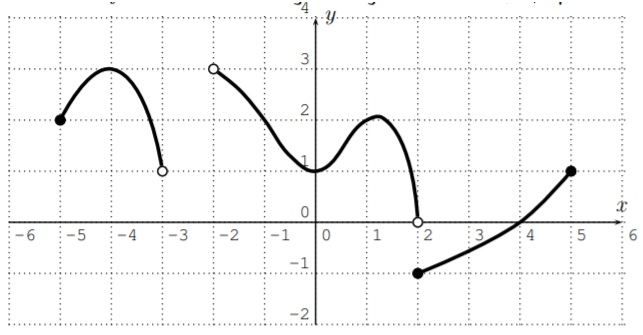
Dejar$f$ ser la función dada por la siguiente gráfica. Encuentra el dominio y la gama de$f$.

$clipboard_e643cc2b8e491cc2edf23381040a6fd85.png$

Solución

Aquí hay algunos valores de función que se pueden leer en la gráfica:

\[\begin{aligned} & f(-5)=2, \quad f(-4)=3, \quad f(-3) \text{ and } f(-2) \text{ are undefined},\\ & f(-1)=2, \quad f(0)=1, \quad f(1)=2, \quad f(2)=-1, \quad f(4)=0, \quad f(5)=1\end{aligned}\]

Tenga en cuenta, que el valor de salida$f(3)$ está en algún lugar entre$-1$ y$0$, pero solo podemos leer una aproximación$f(3)$ de la gráfica.

Para encontrar el dominio de la función, necesitamos determinar todas las$x$ coordenadas posibles (o en otras palabras, necesitamos proyectar la gráfica en el$x$ eje -eje). Las posibles$x$ -coordenadas son del intervalo$[-5,-3)$ junto con los intervalos$(-2,2)$ y$[2,5]$. Los dos últimos intervalos se pueden combinar. Obtenemos el dominio:

\[D=[-5,-3)\cup (-2,5] \nonumber \]

Para el rango, miramos todos los$y$ valores posibles. Estos están dados por los intervalos$(1,3]$ y$(0,3)$ y$[-1,1]$. Combinando estos tres intervalos, obtenemos el rango

\[R=[-1,3] \nonumber \]

Ejemplo$\PageIndex{4}$

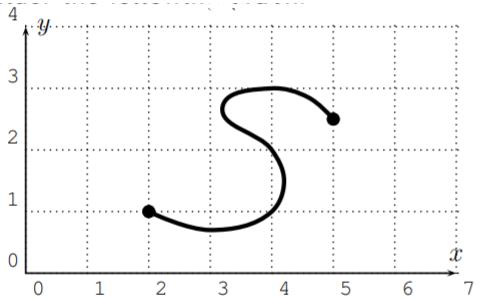
Considera la siguiente gráfica.

$clipboard_e12ef20a4b7a870280969361d2fb94bb1.png$

Solución

Considera la entrada$x=4$. Hay varias salidas que obtenemos$x=4$ de esta gráfica:

\[f(4)=1, \quad f(4)=2, \quad f(4)=3 \nonumber \]

Sin embargo, en una función, ¡no se permite obtener más de una salida para una entrada! Por lo tanto, ¡esta gráfica no es la gráfica de una función! La razón por la que este ejemplo no es una función se debe a que alguna entrada tiene más de una salida:$f(4)=1, f(4)=2, f(4)=3$.

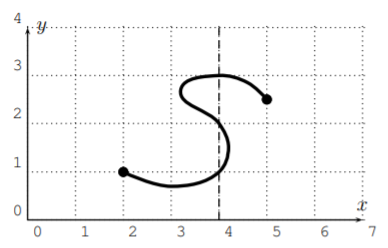
$clipboard_e2cdd04c8fd20029902159d1a0b606efe.png$

En otras palabras, hay una línea vertical ($x=4$) que intersecta la gráfica en más de un punto.

Esta observación se generaliza en la siguiente prueba de línea vertical.

Definición: Prueba de línea vertical

Una gráfica es la gráfica de una función precisamente cuando cada línea vertical se cruza con la gráfica como máximo una vez.

Ejemplo$\PageIndex{5}$

Considera la gráfica de la ecuación$x=y^2$:

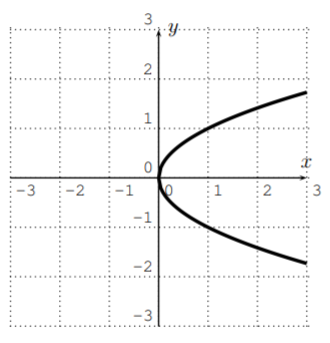
$clipboard_e03db13098ba66526e612b61f27fc14f7.png$

$y$Es una función de$x$?

Solución

Esto no pasa la prueba de línea vertical por lo que no$y$ es una función de$x$. Sin embargo,$x$ es una función de$y$ ya que, si$y$ consideras que es la entrada, cada entrada tiene exactamente una salida (pasa la prueba de 'línea horizontal').

Ejemplo$\PageIndex{6}$

Dejar$f$ ser la función dada por la siguiente gráfica.

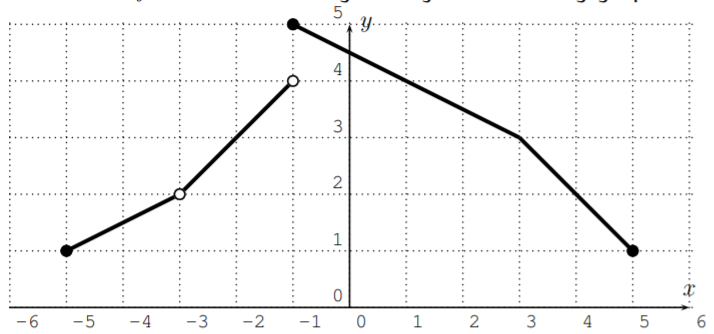
$clipboard_eb7972fa51a8173a63766dfb26f907660.png$

¿De qué es el dominio$f$?
¿Cuál es el rango de$f$?
¿Para cuál$x$ es$f(x)=3$?
¿Para cuál$x$ es$f(x)=2$?
¿Para cuál$x$ es$f(x)>2$?
¿Para cuál$x$ es$f(x)\leq 4$?
Encontrar$f(1)$ y$f(4)$.
Encontrar$f(1)+f(4)$.
Encontrar$f(1)+4$.
Encontrar$f(1+4)$.

La mayoría de las respuestas se pueden leer inmediatamente de la gráfica.

Solución

Para el dominio, proyectamos la gráfica al$x$ eje -eje. El dominio consta de todos los números del$-5$ al$5$ sin$-3$, es decir$D=[-5,-3)\cup (-3,5]$.
Para el rango, proyectamos la gráfica al$y$ eje -eje. El dominio consta de todos los números desde$1$ hasta$5$, es decir$R=[1,5]$.
Para encontrar$x$ con$f(x)=3$ miramos la línea horizontal en$y=3$:
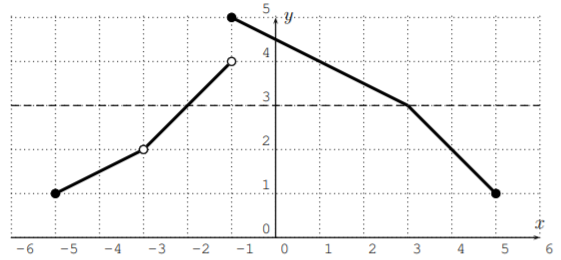
$clipboard_e851ec82396f5f6c62e550f576e6cb078.png$

Vemos que hay dos números$x$ con$f(x)=3$:

\[f(-2)=3, \quad\quad f(3)=3 \nonumber \]

Por lo tanto, la respuesta es$x=-2$ o$x=3$.
Al mirar la línea horizontal$y=2$, vemos que sólo hay una$x$ con$f(x)=2$; es decir$f(4)=2$. Tenga en cuenta, eso$x=-3$ no resuelve el problema, ya que no$f(-3)$ está definido. La respuesta es$x=4$.
Para encontrar$x$ con$f(x)>2$, la gráfica tiene que estar por encima de la línea$y=2$.
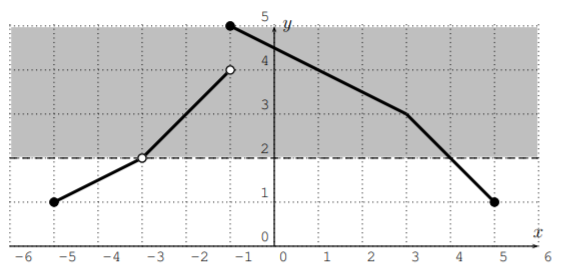
$clipboard_ecfad4c9f0e7cd2678b7db89046636e06.png$

Vemos que la respuesta son esos números$x$ mayores que$-3$ y menores que$4$. La respuesta es, por tanto, el intervalo$(-3,4)$.
Para$f(x)\leq 4$, obtenemos todos los números$x$ del dominio que son menores$-1$ o mayores o iguales a$1$. La respuesta es, por lo tanto,
\[[-5,-3)\cup (-3,-1)\cup [1,5] \nonumber \]

Tenga en cuenta$-3$ que no forma parte de la respuesta, ya que$f(-3)$ es indefinido.
$f(1)=4$, y$f(4)=2$
$f(1)+f(4)=4+2=6$
$f(1)+4=4+4=8$
$f(1+4)=f(5)=1$

Ejemplo$\PageIndex{7}$

La siguiente gráfica muestra el tamaño de la población en una pequeña ciudad en los años 2001-2011 en miles de personas.

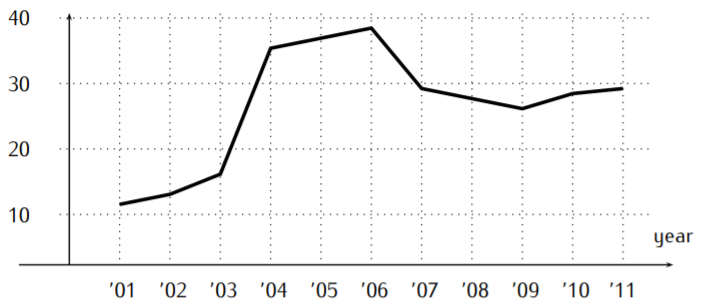
$clipboard_ea06a56b96a4c979cd41f9fede0623261.png$

¿Cuál fue el tamaño de la población en los años 2004 y 2009?
¿En qué años tuvo la ciudad más población?
¿En qué año creció más rápido la población?
¿En qué año disminuyó más rápido la población?

Solución

El tamaño de la población en el año 2004 fue aproximadamente$36,000$. En el año 2009, fue aproximadamente$26,000$.
La población más grande fue en el año 2006, donde la gráfica tiene su máximo.
El crecimiento más rápido en la población fue entre los años 2003 y 2004. Es entonces cuando la gráfica tiene la pendiente más grande.
Por último, el descenso más rápido ocurrió en los años 2006-2007.

Ejemplo$\PageIndex{8}$

Grafique la función descrita por la siguiente fórmula:

\[f(x)=\left\{ \begin{matrix} x+3 & \text{, for}& -3\leq x< -1 \\ x^2 & \text{, for}& -1<x<1 \\ 3 & \text{, for} & 2<x\leq 3 \end{matrix} \right.\nonumber\]

Solución

Realmente tenemos que graficar las tres funciones$y=x+3$,$y=x^2$, y$y=3$, y luego restringirlas a su respectivo dominio. Graficando las tres funciones, obtenemos las siguientes tablas y gráficas asociadas, que dibujamos en un$x$$y$ plano:

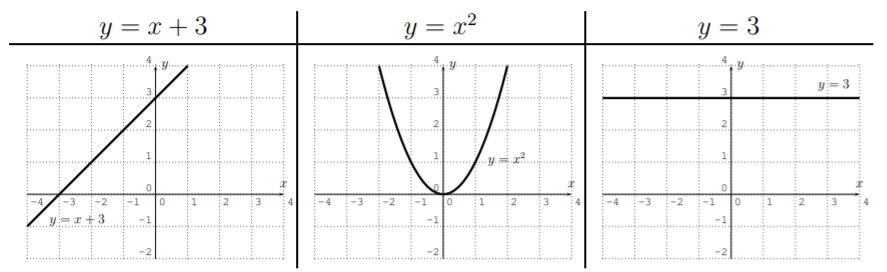
$clipboard_e62b834eefa4b11102a40a93f34651df7.png$

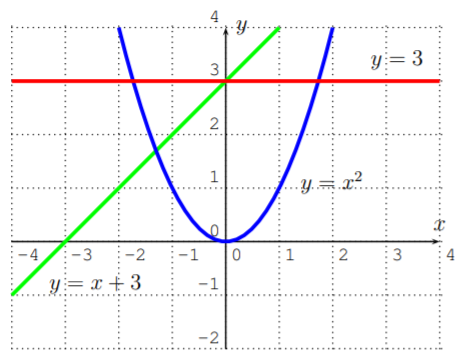
$clipboard_e47d552007dbbeeddc10a20c9ed1479b7.png$

Sin embargo, necesitamos cortar las funciones de acuerdo con su dominio de entrada específico que es dado por la función original.

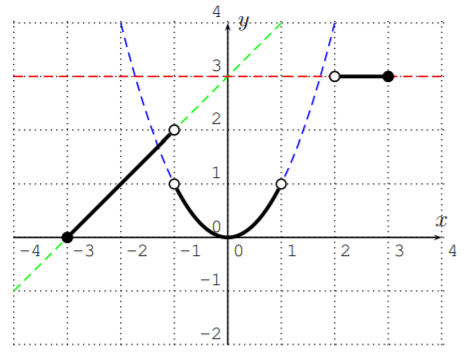
$clipboard_e5c3537205de3fc2788307e43cac5d58a.png$

Observe cómo los círculos abiertos y cerrados en los extremos de cada rama corresponden a las reglas “$<$” y “$\leq$” en la descripción original de la función.

Ejemplo\(\PageIndex{1}\)

Ejemplo\(\PageIndex{2}\)

Ejemplo\(\PageIndex{3}\)

Ejemplo\(\PageIndex{4}\)

Definición: Prueba de línea vertical

Ejemplo\(\PageIndex{5}\)

Ejemplo\(\PageIndex{6}\)

Ejemplo\(\PageIndex{7}\)

Ejemplo\(\PageIndex{8}\)