4.6: Evaluar el riesgo
- Page ID
- 61846
- Explicar la dinámica básica de las probabilidades.
- Discutir cómo se pueden usar las probabilidades para medir el valor esperado.
- Describir cómo se pueden utilizar las probabilidades en las proyecciones financieras.
- Analizar los resultados esperados de las elecciones financieras.
El riesgo afecta la toma de decisiones financieras de formas misteriosas, muchas de las cuales son objeto de toda una área de becas ahora conocida como finanzas conductuales. El estudio del riesgo y la interpretación de las probabilidades son complejos. En la toma de decisiones financieras, es útil comprender su dinámica básica. Una de las más importantes a entender es la idea de independencia.
Un evento independiente es aquel que ocurre por casualidad. No se puede querer ni decidir. La probabilidad o probabilidad de un evento independiente se puede medir, en función de su frecuencia en el pasado, y esa probabilidad se puede utilizar para predecir si se repetirá. Los eventos independientes pueden ser el resultado de situaciones complejas. Se pueden estudiar para ver qué confluencia de circunstancias o condiciones los hacen más o menos probables o afectan su probabilidad. Pero un evento independiente es, al final, por hábilmente analizado que sea, cuestión de alguna casualidad o incertidumbre o riesgo; no puede determinarse ni elegirse.
Figura 4.6.1
© 2010 Corporación Jupiterimages
Alice puede elegir si ir o no a Las Vegas, pero no puede elegir si gana o no. Ganar o perder es un evento independiente. Ella puede predecir sus posibilidades, la probabilidad, de que gane en base a sus experiencias pasadas, su aparente habilidad y conocimiento, y las probabilidades conocidas de los juegos de azar de casino (sobre las cuales se han realizado muchos estudios y hay mucho conocimiento disponible). Pero no puede elegir ganar; siempre hay cierta incertidumbre o riesgo de que no lo haga.
La probabilidad de cualquier resultado para un evento siempre se establece como un porcentaje del total de resultados posibles. Un evento independiente o riesgoso tiene al menos dos posibles resultados: sucede o no sucede. Puede haber más resultados posibles, pero hay al menos dos; si solo hubiera un resultado posible, no habría incertidumbre ni riesgo sobre el resultado.
Por ejemplo, tienes una “probabilidad 50-50” de “cabezas” cuando lanzas una moneda, o una probabilidad del 50 por ciento. En promedio “cabezas” aparece la mitad del tiempo. Esa probabilidad se basa en la frecuencia histórica; es decir, “en promedio” significa que por todas las veces que se han volteado las monedas, la mitad del tiempo “cabezas” es el resultado. Solo hay dos resultados posibles cuando lanzas una moneda, y hay un 50 por ciento de probabilidad de cada uno. Las probabilidades de cada posible resultado suman hasta el 100 por ciento, porque hay 100 por ciento de probabilidad de que algo suceda. En este caso, la mitad del tiempo es un resultado, y la mitad del tiempo es el otro. En general, las probabilidades de cada posible resultado —y puede haber muchos— se suman al 100 por ciento.
Las probabilidades se pueden utilizar en las decisiones financieras para medir el resultado esperado de un evento independiente. Esa expectativa se basa en las probabilidades de cada resultado y su resultado si ocurre. Supongamos que tienes una pequeña apuesta que va en el flip de la moneda; ganarás un dólar si te sube “cabezas” y perderás un dólar si no lo hace (“colas”). Tienes una probabilidad del 50 por ciento de $1.00 y una probabilidad del 50 por ciento de −$1.00. La mitad del tiempo se puede esperar ganar un dólar, y la mitad del tiempo se puede esperar perder un dólar. Su expectativa del resultado promedio, basada en la frecuencia o probabilidad histórica de cada resultado y su resultado real, es
(0.50×1.00) + (0.50×−1.00) =0.50+−0.50=0, o (cabezas de probabilidad × cabezas de resultado) + (colas de probabilidad × colas de resultados)
—note que las cabezas de probabilidad + las colas de probabilidad = 1 o 100% —porque esos son todos los resultados posibles. El resultado esperado para cada resultado es su probabilidad o probabilidad multiplicada por su resultado. El resultado esperado o valor esperado para la acción, por voltear una moneda, es su resultado promedio ponderado, siendo los “pesos” las probabilidades de cada uno de sus resultados.
Si obtienes $1.00 cada vez que la moneda voltea “cabezas” y lo hace la mitad del tiempo, entonces la mitad del tiempo obtienes un dólar, o puedes esperar que en general te des cuenta de medio dólar o $0.50 al voltear “cabezas”. La otra mitad del tiempo, se puede esperar perder un dólar, por lo que su expectativa tiene que incluir la posibilidad de voltear “colas” con un resultado general o promedio de perder $0.50 o −$0.50. Entonces puedes esperar 0.50 de un resultado y −0.50 del otro: en conjunto, puedes esperar 0.50 + −0.50 o 0 (razón por la cual “voltear monedas” no es un juego de casino popular).
El valor esperado (E (V)) de un evento es la suma de la probabilidad de cada posible resultado multiplicada por su resultado, o
E (V) =σ (p n × r n),
donde σ significa suma, p es la probabilidad de un resultado, r es su resultado y n es el número de resultados posibles.
Ante la incertidumbre de una alternativa que involucra un evento independiente, a menudo resulta bastante útil poder al menos calcular su valor esperado. Entonces, al tomar una decisión, esa expectativa puede sopesarse contra o compararse con las de otras elecciones.
Figura 4.6.2
© 2010 Corporación Jupiterimages
Por ejemplo, Alice ha proyectado cuatro posibles resultados para sus finanzas dependiendo de si continúa, consigue un segundo trabajo, gana en Las Vegas o pierde en Las Vegas, pero en realidad solo hay tres opciones: continuar, segundo trabajo o ir a Las Vegas, ya que ganar o perder son resultados de la única decisión de ir a Las Vegas. Ella sabe, con poca o ninguna incertidumbre, cómo se verá su situación financiera si continúa o consigue un segundo empleo. Para comparar la elección de Las Vegas con las otras dos, necesita predecir qué puede esperar de ir a Las Vegas, dado que puede ganar o perder una vez allí.
Alice puede calcular el resultado esperado de ir a Las Vegas si conoce las probabilidades de sus dos resultados, ganar y perder. Alice investiga un poco y hace que una amiga le muestre algunos trucos y decide que para ella la probabilidad de ganar es del 30 por ciento, lo que hace que la probabilidad de perder el 70 por ciento. (Como en este caso sólo hay dos posibles resultados, sus probabilidades deben sumar al 100 por ciento.) Su resultado esperado en Las Vegas, entonces, es
(0.30×100,000) + (0.70×−100,000) =30.000+−70.000=−40,000.
Utilizando los mismos cálculos, puede proyectar el resultado esperado de ir a Las Vegas en sus estados financieros pro forma (Figura 4.21). Mira el efecto en sus resultados:
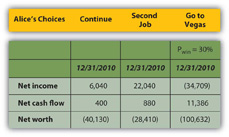
Si solo tiene un 30 por ciento de posibilidades de ganar en Las Vegas, entonces ir allí es la peor opción para ella en términos de su ingreso neto y patrimonio neto. Su flujo de caja neto (CF) en realidad parece mejor con la opción de Las Vegas, pero eso supone que puede pedir prestado para pagar sus pérdidas de juego, por lo que sus pérdidas no crean un flujo de caja neto negativo. Ella sí, sin embargo, crea deuda.
Alice también puede calcular cuál tendría que ser la probabilidad de ganar para que sea una elección que valga la pena, es decir, darle al menos un resultado tan bueno como cualquiera de sus otras opciones (Figura 4.22).
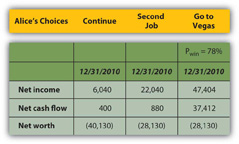
Para ser la mejor opción en términos de los tres resultados finales, Alice tendría que tener un 78 por ciento de posibilidades de ganar en Las Vegas.
Su patrimonio neto seguiría siendo negativo, pero los tres resultados serían al menos tan buenos o mejores de lo que serían con sus otras dos opciones. Si Alice pensara que tenía al menos un 78 por ciento de posibilidades de ganar y pudiera tolerar el riesgo de que no, Las Vegas sería una opción viable para ella.
Esos son dos “ifs” muy grandes, pero al poder proyectar un valor o resultado esperado para cada una de sus elecciones, usando las probabilidades de cada resultado para la elección con incertidumbre, Alice puede al menos medir y comparar las elecciones.
El uso de probabilidades para derivar el valor esperado de una elección proporciona una manera de evaluar una alternativa con incertidumbre. Requiere proyectar las probabilidades y resultados de cada posible resultado o evento independiente. No puede eliminar la incertidumbre o el riesgo que presenta la independencia, pero al menos puede proporcionar una manera de medir y luego comparar con otras opciones medibles, ciertas o inciertas.
- Las probabilidades se pueden utilizar en las decisiones financieras para medir el resultado esperado de un evento independiente.
- El valor esperado para una elección puede calcularse como E (V) = σ (p n × r n).
- El valor esperado se puede ponderar o comparar con los valores de otras opciones.
Ejercicios
- ¿Cómo se utilizan las probabilidades en las decisiones financieras?
- ¿Cómo se pueden calcular los valores esperados de las alternativas financieras?
- Comparada con sus otras dos opciones y sus metas financieras, ¿Alice debería ir a Las Vegas? ¿Por qué, o por qué no?
- Lee la explicación del valor esperado y su aplicación al poker jugando en CardsChat: The Worldwide Poker Community (www.cardschat.com/poker-odds-... cted-value.php). Alice podría haber usado información similar para calcular sus posibilidades de ganar en Las Vegas.