3.7: Aplicación- Valores de Probabilidad y Expectativa
- Page ID
- 111222
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)En esta sección discutiremos brevemente algunas aplicaciones de integrales múltiples en el campo de la teoría de probabilidad. En particular veremos formas en las que se pueden usar múltiples integrales para calcular probabilidades y valores esperados.
Probabilidad
Supongamos que tiene un troquel estándar de seis lados (justo), y deja que una variable\(X\) represente el valor rodado. Entonces la probabilidad de rodar un 3, escrito como\(P(X = 3)\), es de 1 6, ya que hay seis lados en el dado y cada uno es igualmente probable que sea enrollado, y de ahí en particular el 3 tiene una probabilidad de uno de seis de ser rodado. De igual manera la probabilidad de rodar como máximo un 3\(P(X ≤ 3)\), escrito como\(\dfrac{3}{ 6} = \dfrac{1}{ 2}\), es, ya que de los seis números en el dado, hay tres números igualmente probables (1, 2 y 3) que son menores o iguales a 3. Tenga en cuenta que:
\[P(X ≤ 3) = P(X = 1) + P(X = 2) + P(X = 3).\]
Llamamos a\(X\) una variable aleatoria discreta en el espacio muestral (o espacio de probabilidad)\(Ω\) que consiste en todos los resultados posibles. En nuestro caso,\(Ω = {1,2,3,4,5,6}\). Un evento\(A\) es un subconjunto del espacio de muestra. Por ejemplo, en el caso del dado, el suceso\(X ≤ 3\) es el conjunto\({1,2,3}\).
Ahora deja\(X\) ser una variable que representa un número real aleatorio en el intervalo\((0,1)\). Tenga en cuenta que el conjunto de todos los números reales entre 0 y 1 no es un conjunto discreto (o contable) de valores, es decir, no se puede poner en una correspondencia uno a uno con el conjunto de enteros positivos. En este caso, para cualquier número real\(x\) en\((0,1)\), no tiene sentido considerar\(P(X = x)\) ya que debe ser 0 (¿por qué?). En cambio, consideramos la probabilidad\(P(X ≤ x)\), que viene dada por\(P(X ≤ x) = x\). El razonamiento es el siguiente: el intervalo\((0,1)\) tiene longitud 1, y para\(x\) en\((0,1)\) el intervalo\((0, x)\) tiene longitud\(x\). Entonces, dado que\(X\) representa un número aleatorio en\((0,1)\), y por lo tanto se distribuye uniformemente sobre\((0,1)\), entonces
\[P(X ≤ x) = \dfrac{\text{length of }(0, x)}{\text{length of }(0,1)}=\dfrac{x}{1}=x\]
Llamamos a\(X\) una variable aleatoria continua en el espacio muestral\(Ω = (0,1)\). Un evento\(A\) es un subconjunto del espacio de muestra. Por ejemplo, en nuestro caso el evento\(X ≤ x\) es el set\((0, x)\).
En el caso de una variable aleatoria discreta, vimos cómo la probabilidad de un evento era la suma de las probabilidades de los resultados individuales que comprenden ese evento (por ejemplo,\(P(X ≤ 3) = P(X = 1) + P(X = 2) + P(X = 3)\) en el ejemplo dado). Para una variable aleatoria continua, la probabilidad de un evento será en cambio la integral de una función, que ahora describiremos.
Dejar\(X\) ser una variable aleatoria de valor real continua en un espacio de muestra\(Ω\) en\(\mathbb{R}\). Por simplicidad, vamos\(Ω = (a,b)\). Definir la función\(F\) de distribución de\(X\) como
\[ \begin{align}F(x)&=P(X ≤ x) ,\quad \text{for }-\infty < x <\infty \label{Eq3.33} \\[4pt] &= \cases{1, \quad \quad \quad \, \, \, \, \,\text{for }x \ge b \\[4pt] P(X \le x), \quad \text{for }a<x<b \label{Eq3.34} \\[4pt] 0, \quad \quad \quad \, \, \, \, \, \text{for } x \le a . }\end{align}\]
Supongamos que hay una función no negativa, continua de valor real\(f\) en\(\mathbb{R}\) tal que
\[F(x) = \int_{-\infty}^x f (y)\,d y ,\quad \text{for }-\infty < x < \infty, \label{Eq3.35}\]
y
\[\int_{-\infty}^{\infty} f(x)\,dx=1 \label{Eq3.36}\]
Entonces llamamos a\(f\) la función de densidad de probabilidad (o\(p.d.f\). para abreviar) para\(X\). Por lo tanto, tenemos
\[P(X ≤ x) = \int_a^x f (y)\,d y , \quad \text{for }a<x<b \label{Eq3.37}\]
También, por el Teorema Fundamental del Cálculo, tenemos
\[F'(x)=f(x),\quad \text{for }-\infty < x < \infty .\label{Eq3.38}\]
Ejemplo\(\PageIndex{1}\): Uniform Distribution
Dejar\(X\) representar un número real seleccionado aleatoriamente en el intervalo\((0,1)\). Decimos que\(X\) tiene la distribución uniforme encendida\((0,1)\), con función de distribución
\[F(x) = P(X ≤ x) = \cases{1,\quad \text{for }x \ge 1 \\[4pt] x, \quad \text{for } 0<x<1 \\[4pt] 0, \quad \text{for }x \le 0,}\label{Eq3.39}\]
y función de densidad de probabilidad
\[f(x)=F'(x)=\cases{1,\quad \text{for }0<x<1 \\[4pt] 0,\quad \text{elsewhere.}}\label{Eq3.40}\]
En general, si\(X\) representa un número real seleccionado aleatoriamente en un intervalo\((a,b)\), entonces\(X\) tiene la función de distribución uniforme
\[F(x)=P(X ≤ x)=\cases{1,\quad &\text{for }x \ge b \\[4pt] \dfrac{x}{b-a}, &\text{for }a<x<b \\[4pt] 0, &\text{for }x \le a}\label{Eq3.41}\]
\[f (x) = F ′ (x) =\cases{\dfrac{1}{b-a},\quad &\text{for }a<x<b \\[4pt] 0,&\text{elsewhere.}}\label{Eq3.42}\]
Ejemplo\(\PageIndex{2}\): Standard Normal Distribution
Una función de distribución famosa viene dada por la distribución normal estándar, cuya función de densidad de probabilidad\(f\) es
\[f (x) = \dfrac{1}{\sqrt{2\pi}}e^{-x^2/2},\quad \text{for }-\infty <x< \infty \label{Eq3.43}\]
Esto a menudo se llama “curva de campana”, y se usa ampliamente en estadística. Ya que estamos reclamando que\(f\) es una\(p.d.f.\), deberíamos haber
\[\int_{-\infty}^{\infty} \dfrac{1}{\sqrt{2\pi}}e^{-x^2/2}\, dx=1\label{Eq3.44}\]
por Ecuación\ ref {Eq3.36}, que es equivalente a
\[\int_{-\infty}^{\infty}e^{-x^2/2}\,dx = \sqrt{2\pi}.\label{Eq3.45}\]
Podemos usar una doble integral en coordenadas polares para verificar esta integral. En primer lugar,
\[\nonumber \begin{align} \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} e^{-(x^2+y^2)/2} \, dx\,dy &= \int_{-\infty}^{\infty} e^{-y^2/2} \left ( \int_{-\infty}^{\infty}e^{-x^2/2}\,dx \right )\, dy \\[4pt] \nonumber &=\left ( \int_{-\infty}^{\infty} e^{-x^2/2}\,dx \right ) \left ( \int_{-\infty}^{\infty} e^{-y^2/2}\,dy \right ) \\[4pt] \nonumber &=\left ( \int_{-\infty}^{\infty} e^{-x^2/2}\,dx \right )^2 \\[4pt] \end{align}\]
ya que la misma función se está integrando dos veces en la ecuación media, solo con diferentes variables. Pero usando coordenadas polares, vemos que
\[\nonumber \begin{align} \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} e^{-(x^2+y^2)/2} \, dx\,dy &=\int_0^{2\pi} \int_0^\infty e^{-r^2/2}\,r\,dr\,dθ \\[4pt] \nonumber &=\int_0^{2\pi} \left (-e^{-r^2/2} \Big |_{r=0}^{r=\infty} \right )\,dθ \\[4pt] \nonumber &=\int_0^{2\pi} (0-(-e^0))\,dθ = \int_0^{2\pi}1\,dθ=2\pi , \\[4pt] \end{align}\]
y así
\[\nonumber \begin{align}\left ( \int_{-\infty}^{\infty} e^{-x^2/2}\,dx \right )^2 &= 2\pi,\text{ and hence }\\[4pt] \nonumber \int_{-\infty}^{\infty} e^{-x^2/2}\,dx &= \sqrt{2\pi} \\[4pt] \end{align}\]
Además de las variables aleatorias individuales, podemos considerar variables aleatorias distribuidas conjuntamente. Para ello, dejaremos\(X, Y \text{ and }Z\) ser tres variables aleatorias continuas de valor real definidas en el mismo espacio muestral\(Ω\) en\(\mathbb{R}\) (la discusión para dos variables aleatorias es similar). Entonces la función de distribución conjunta\(F \text{ of }X, Y \text{ and }Z\) viene dada por
\[F(x, y, z) = P(X ≤ x, Y ≤ y, Z ≤ z) ,\text{ for }-\infty < x,y,z < \infty. \label{Eq3.46}\]
Si hay una función no negativa, continua de valor real\(f\) en\(\mathbb{R}^ 3\) tal que
\[F(x,y,z) = \int_{-\infty}^z \int_{-\infty}^y \int_{-\infty}^x f (u,v,w)\,du\, dv\, dw, \text{ for }-\infty <x,y,z< \infty \label{Eq3.47}\]
y
\[\int_{-\infty}^{\infty} \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} f (x, y, z)\,dx\, d y\, dz = 1 ,\label{Eq3.48}\]
entonces llamamos a\(f\) la función de densidad de probabilidad conjunta (o p.d.f conjunta para abreviar) para\(X, Y \text{ and }Z\). En general, para\(a_1 < b_1 , a_2 < b_2 , a_3 < b_3\), tenemos
\[P(a_1 < X ≤ b_1 , a_2 < Y ≤ b_2 , a_3 < Z ≤ b_3) = \int_{a_3}^{b_3} \int_{a_2}^{b_2} \int_{a_1}^{b_1}f (x, y, z)\,dx\, d y\, dz ,\label{Eq3.49}\]
con los\(\le \text{ and }<\) símbolos intercambiables en cualquier combinación. Una triple integral, entonces, puede pensarse como que representa una probabilidad (para una función\(f\) que es a\(p.d.f.\)).
Ejemplo\(\PageIndex{3}\)
Let\(a, b, \text{ and }c\) Ser números reales seleccionados aleatoriamente del intervalo\((0,1)\). ¿Cuál es la probabilidad de que la ecuación\(ax^2 + bx+ c = 0\) tenga al menos una solución real\(x\)?
Solución
Sabemos por la fórmula cuadrática que hay al menos una solución real si\(b^2−4ac ≥ 0\). Entonces tenemos que calcular\(P(b^2−4ac ≥ 0)\). Utilizaremos tres variables aleatorias distribuidas conjuntamente para hacer esto. Primero, ya\(0 < a,b, c < 1,\) que tenemos
\[\nonumber b^2 −4ac ≥ 0 ⇔ 0 < 4ac ≤ b^2 < 1 ⇔ 0 < 2 \sqrt{ a} \sqrt{ c} ≤ b < 1 ,\]
donde la última relación se sostiene para todos\(0 < a, c < 1\) tales que
\[\nonumber 0 < 4ac < 1 ⇔ 0 < c < \dfrac{1}{4a}\]
Considerando\(a, b \text{ and }c\) como variables reales, la región\(R\) en el\(ac\) -plano donde se sostiene la relación anterior viene dada por\(R = {(a, c) : 0 < a < 1, 0 < c < 1, 0 < c < \dfrac{1}{4a} }\), lo que podemos ver es una unión de dos regiones\(R_1\) y\(R_2\), como en la Figura\(\PageIndex{1}\).
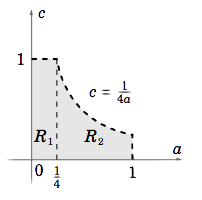
Ahora vamos a\(X, Y \text{ and }Z\) ser variables aleatorias continuas, cada una representando un número real seleccionado aleatoriamente del intervalo\((0,1)\) (piense en\(X, Y \text{ and }Z\) representar\(a, b \text{ and }c\), respectivamente). Entonces, similar a como demostramos que\(f (x) = 1\) es la\(p.d.f.\) de la distribución uniforme en\((0,1)\), se puede mostrar que\(f (x, y, z) = 1 \text{ for }x, y, z\) en\((0,1)\) (0 en otra parte) es la articulación\(p.d.f. \text{ of }X, Y \text{ and }Z\). Ahora,
\[\nonumber P(b^2 −4ac ≥ 0) = P((a, c) ∈ R, 2 \sqrt{ a} \sqrt{ c} ≤ b < 1) ,\]
por lo que esta probabilidad es la triple integral de\(f (a,b, c) = 1\) como b varía de\(2\sqrt{ a}\sqrt{c}\) a 1 y como\((a, c)\) varía a lo largo de la región\(R\). Dado que se\(R\) puede dividir en dos regiones\(R_1 \text{ and }R_2\), entonces la triple integral requerida se puede dividir en una suma de dos integrales triples, usando cortes verticales en\(R\):
\[\nonumber \begin{align} P(b^2 −4ac ≥ 0) &= \underbrace{\int_0^{1/4} \int_0^1}_{R_1}\int_{2\sqrt{a}\sqrt{c}}^1 1\,db\, dc\, da + \underbrace{\int_{1/4}^1 \int_0^{1/4a}}_{R_2} \int_{2\sqrt{a}\sqrt{c}}^1 1\,db\, dc\, da \\[4pt] \nonumber &= \int_0^{1/4} \int_0^1 (1−2 \sqrt{ a} \sqrt{ c})dc \,da + \int_{1/4}^1 \int_0^{1/4a}(1−2 \sqrt{ a} \sqrt{ c})dc\, da \\[4pt] \nonumber &= \int_0^{1/4} \left ( c-\dfrac{4}{3}\sqrt{a}c^{3/2}\Big |_{c=0}^{c=1} \right )\,da+\int_{1/4}^1 \left (c-\dfrac{4}{3}\sqrt{a}c^{3/2}\Big |_{c=0}^{c=1/4a} \right )\,da \\[4pt] \nonumber &=\int_0^{1/4} \left (1-\dfrac{4}{3}\sqrt{a} \right )\,da+\int_{1/4}^1 \dfrac{1}{12a}\,da \\[4pt] \nonumber &=a-\dfrac{8}{9}a^{3/2} \Big |_0^{1/4}+\dfrac{1}{12}\ln a \Big |_{1/4}^1 \\[4pt] \nonumber &=\left (\dfrac{1}{4}-\dfrac{1}{9} \right ) + \left (0-\dfrac{1}{12}\ln \dfrac{1}{4} \right ) = \dfrac{5}{36} + \dfrac{1}{12}\ln 4 \\[4pt] \nonumber P(b^2 −4ac ≥ 0) &= \dfrac{5+3\ln 4}{36} \approx 0.2544 \\[4pt] \end{align}\]
En otras palabras, ¡la ecuación\(ax^2 + bx+ c = 0\) tiene alrededor de un 25% de posibilidades de ser resuelta!
Valor Expectativo
El valor de expectativa (o valor esperado)\(EX\) de una variable aleatoria\(X\) puede considerarse como el valor “promedio” de a\(X\) medida que varía a lo largo de su espacio muestral. Si\(X\) es una variable aleatoria discreta, entonces
\[EX = \sum_x xP(X = x) ,\label{Eq3.50}\]
tomando la suma sobre todos los elementos\(x\) del espacio muestral. Por ejemplo, si\(X\) representa el número enrollado en una matriz de seis caras, entonces
\[EX = \sum_{x=1}^6 x P(X = x) = \sum_{x=1}^6 x\dfrac{1}{6} = 3.5 \label{Eq3.51}\]
es el valor esperado de\(X\), que es el promedio de los enteros 1−6.
Si\(X\) es una variable aleatoria continua de valor real con p.d.f.\(f\), entonces
\[EX = \int_{-\infty}^\infty x f (x)\,dx \label{Eq3.52}\]
Por ejemplo, si\(X\) tiene la distribución uniforme en el intervalo\((0,1)\), entonces su p.d.f. es
\[f(x) = \cases{1, \quad &\text{for }0 < x < 1 \\[4pt] 0,&\text{elsewhere}}\label{Eq3.53}\]
y así
\[EX=\int_{-\infty}^\infty x f (x)\,dx = \int_0^1 x\,dx = \dfrac{1}{2} \label{Eq3.54}\]
Para un par de variables aleatorias continuas de valor real distribuidas conjuntamente\(X\) y\(Y\) con p.d.f conjunta\( f (x, y)\), los valores esperados de\(X \text{ and }Y\) están dados por
\[EX = \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} xf(x,y)\,dx\,dy \text{ and } EY = \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} yf(x,y)\,dx\,dy \label{Eq3.55}\]
respectivamente.
Ejemplo\(\PageIndex{4}\)
Si escogieras números reales\(n > 2\) aleatorios del intervalo\((0,1)\), ¿cuáles son los valores esperados para el menor y el mayor de esos números?
Solución
Dejar\(U_1 ,...,U_n\) ser variables aleatorias\(n\) continuas, cada una representando un número real seleccionado aleatoriamente de\((0,1)\), es decir, cada una tiene la distribución uniforme encendida\((0,1)\). Definir variables aleatorias\(X \text{ and }Y\) por
\[\nonumber X=\text{min}(U_1,...,U_n)\text{ and }Y=\text{max}(U_1,...,U_n).\]
Entonces se puede demostrar que el p.d.f. conjunto de\(X \text{ and }Y\) es
\[f(x,y) = \cases{n(n−1)(y− x)^{n−2},\quad &\text{for } 0 ≤ x ≤ y ≤ 1 \\[4pt] 0, &\text{elsewhere.}}\label{Eq3.56}\]
Así, el valor esperado de\(X\) es
\[\nonumber \begin{align} EX &=\int_0^1 \int_x^1 n(n−1)x(y− x)^{n−2}\, d y\, dx \\[4pt] \nonumber &=\int_0^1 \left ( nx(y− x)^{n−1} \Big |_{y=x}^{y=1} \right )\,dx \\[4pt] \nonumber &=\int_0^1 nx(1− x)^{n−1}\, dx,\text{ so integration by parts yields} \\[4pt] \nonumber &=−x(1− x)^n − \dfrac{1}{n+1} (1− x)^{n+1} \Big |_0^1 \\[4pt] \nonumber EX&=\dfrac{1}{n+1}, \\[4pt] \end{align}\]
y de manera similar (ver Ejercicio 3) se puede demostrar que
\[\nonumber EY = \int_0^1 \int_0^y n(n−1)y(y− x)^{n−2}\, dx\, d y = \dfrac{n}{n+1}.\]
Entonces, por ejemplo, si tuviera que tomar repetidamente muestras de números reales\(n = 3\) aleatorios de\((0,1)\), y cada vez almacenar los valores mínimo y máximo en la muestra, entonces el promedio de los mínimos se acercaría\(\dfrac{1}{ 4}\) y el promedio de los máximos se acercaría\(\dfrac{3}{ 4}\) como el número de las muestras crecen. Sería relativamente sencillo (ver Ejercicio 4) escribir un programa de computadora para probar esto.


